珠三角地区典型海相沉积软黏土蠕变特性试验研究
2018-11-19王祥秋胡子萱朱道立
王祥秋,胡子萱,朱道立
(佛山科学技术学院交通与土木建筑学院,广东佛山528000)
珠三角地区分布着大量深厚的海相沉积软土,海相沉积软土主要是淤泥以及淤泥质软土,其主要工程特征为:低承载力、高含水率、高压缩性、高触变性以及显著的流变特性[1]。海相沉积软土的变形不仅与应力水平有关,还与作用时间有关。广义的流变包括:蠕变、应力松弛、长期强度、弹性后效和滞后效应[2]。在海相沉积软土地区进行基坑开挖,由于开挖扰动造成软土流变,将会使基坑支护结构及周围环境产生随时间变化的变形[3],而基坑的开挖形状、顺序、支护时间和坑边超载等因素,也会影响基坑的变形,最终导致基坑支护结构和周围环境变形产生明显的时空效应[4]。
为了保证基坑开挖的施工安全,需要对基坑的时空效应进行深入细致的研究。在珠三角地区,广泛分布的淤泥质软黏土是造成基坑时空效应的主要因素,因此,对软黏土进行试验研究,分析其应力应变随时间变化的规律,对于合理解释基坑时空效应以及有效防治基坑开挖时土体产生的过大变形具有重要意义。为此,国内外研究人员对软土的流变力学行为做了大量的研究工作,取得了许多研究成果。近年来许多学者就软土流变特性基于室内三轴流变剪切试验仪对试样进行不同围压、不同排水条件下的流变试验,研究了土体的应力应变与围压及排水条件的关系[5-8]。陈宗基、LEI Huayang等[9-10]结合软土的微观试验,对软土的蠕变特性作了定性的描述。邓岳保、李锐铎、余湘娟、孙明乾等[11-14]通过软土的宏观流变试验,依据理论模型、元件模型、经验模型的各自特点,建立了相关的流变本构模型,为分析掌握软土流变特性奠定了良好的基础。但由于软土流变特性具有显著的区域特征,有必要针对各地区软粘土特殊的流变力学性态深入开展研究。
目前,对珠三角地区软土流变特性的研究鲜有报道,本文针对珠三角地区海相沉积软土,利用三轴剪切蠕变试验仪,开展不同围压下固结不排水剪切蠕变试验,以深入分析其蠕变变形特性。
1 淤泥质软黏土蠕变试验
1.1 试验设备
采用江苏省粟阳市永昌工程试验仪器厂生产FSY-6型非饱和土三轴蠕变试验仪,系统主要由三轴压力室、轴向变形量测系统、轴向力加载系统、数据采集器、计算机等组成。试验所用软黏土取自珠三角地区某工地,属海相沉积软黏土,取土深度为6 m左右,土样物理性质指标如表1所示。

表1 试验土体物理力学性质指标
1.2 试样制备
为了更好地反映原位软粘土的力学性态,本次试验采用大尺寸试样,试样直径68.1 mm,高125 mm。试样制备严格执行《土工试验方法标准》(GB/T50123-1999)。
1.3 试样排水条件
考虑到珠三角地区地下水位较高,淤泥质软土基本上处于饱和状态,并且渗透系数很小,因此,蠕变试验采用固结不排水剪切试验方法。由于地下工程常见的开挖或者埋置深度约为20 m,其侧向土压力强度约为200 kPa左右。因此,分别取围压为100 kPa、150 kPa和200 kPa 3种情况,对土样进行三轴固结不排水剪切蠕变试验。
1.4 加载方式及蠕变稳定标准
本文采用分级加载的方式做蠕变试验并结合实际情况取加载的应力水平为12.5 kPa。文献[15]取软土蠕变试验稳定标准为:当24 h内蠕变量小于0.01 mm时,再加载下一级应力水平。
2 试验结果及分析
3种围压条件下的全过程加载曲线如图1所示,利用“陈氏加载法”[16]可将分级加载下的全过程蠕变曲线转换为各级应力水平下的蠕变试验曲线,其结果如图2所示。
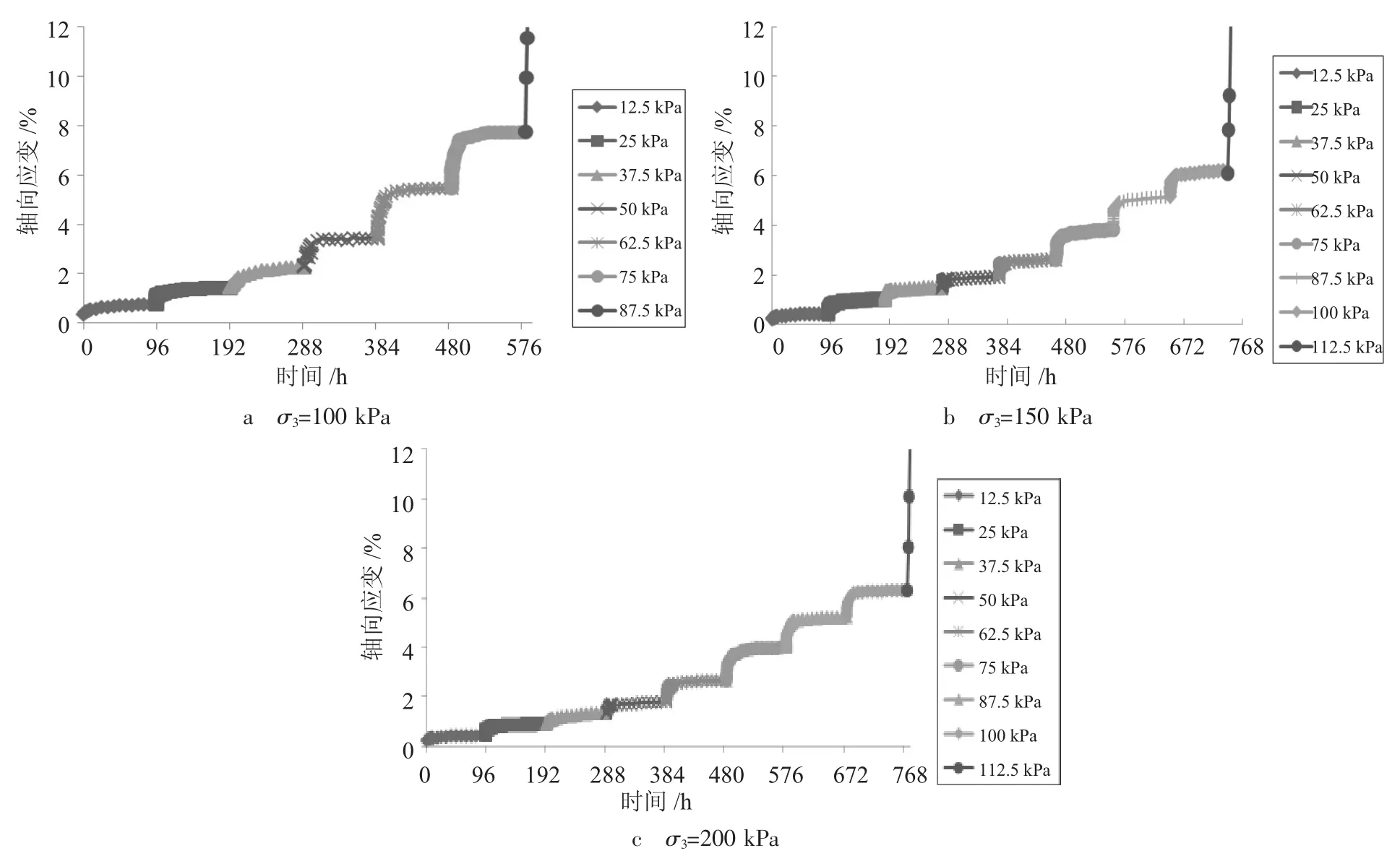
图1 分级增量加载蠕变试验曲线
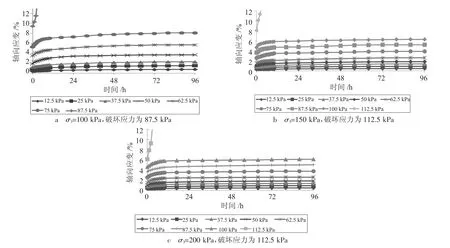
图2 各级应力水平下蠕变试验曲线
由图2可知,珠三角地区海相沉积软黏土具有明显的蠕变特性。不同围压作用下,软土的蠕变过程基本相似,当加载应力水平低于破坏应力的15%时,加载瞬时变形量与蠕变变形量均很小,其蠕变变形量可以忽略不计;随着加载应力水平的不断提高,且加载应力水平达到破坏应力15%~90%时,在加载瞬时会产生明显的弹塑性变形,且随加载历时的不断增大产生明显的蠕变变形,但由于本阶段土体未发生结构性破坏,随着时间推移,土体变形量最终趋于稳定;当加载应力水平达到90%~100%破坏应力时,软土变形量瞬间加大,并很快导致试件发生宏观破坏,加速蠕变阶段历时很短。与此同时,由蠕变试验曲线可知,3种不同围压条件下,软粘土蠕变曲线表现出相似的变化规律,但蠕变变形发展过程以及蠕变变形量存在较大差异。即当偏差应力水平相同时,围压越大,试件瞬时变形和蠕变变形量越小,试件破坏所对应的偏差应力水平越高,而破坏时所产生的轴向应变越小。
为了进一步研究海相沉积淤泥质软黏土的非线性蠕变特性,对以上蠕变试验曲线进行处理[17]可得围压分别为100 kPa、150 kPa和200 kPa时,海相沉积软土的应力应变等时曲线,如图3所示。
由图3可知,珠三角地区淤泥质软黏土应力—应变等时曲线为一簇弯曲的放射性曲线,说明其具有明显的非线性流变特性。同一应力水平下,加载时间越长,应力—应变等时曲线偏向应变轴的程度越大,说明其非线性程度随时间的增加而增强。在试验条件相同的情况下,围压越小,应力—应变等时曲线越偏向于应变轴,说明围压越小,软土的蠕变特性越明显;当应力水平小于屈服应力时,应力—应变等时曲线呈直线状态,表明土体处于线性黏弹性变形阶段。当应力水平大于屈服应力时,其应力—应变等时曲线产生明显的转折,其蠕变变形速率加大,说明软土已进入黏塑性变形状态。由图3可知,珠三角地区海相沉积软黏土的变形呈非线性黏弹塑性。
3 软黏土非线性流变本构模型
根据珠三角地区淤泥质软黏土的应力—应变等时曲线,可将软土的总应变分为线性蠕变和非线性蠕变部分,线性蠕变可用理论模型进行模拟,而非线性流变部分可用经验模型予以模拟。采用切线法对应力—应变等时曲线进行分解[18],可得软粘土的线性黏弹性应变、线性黏塑性应变和非线性黏塑性应变分量,具体分解过程如图4所示。根据蠕变变形分解结果,采用组合模型模拟珠三角地区淤泥质软黏土的蠕变性态,其模型结构由线性黏弹性模型、线性黏塑性模型和非线性黏塑性模型串联组合而成,具体模型结构如图5所示。
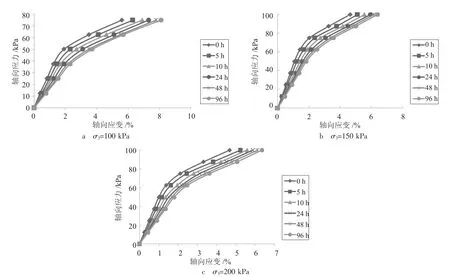
图3 应力—应变等时曲线
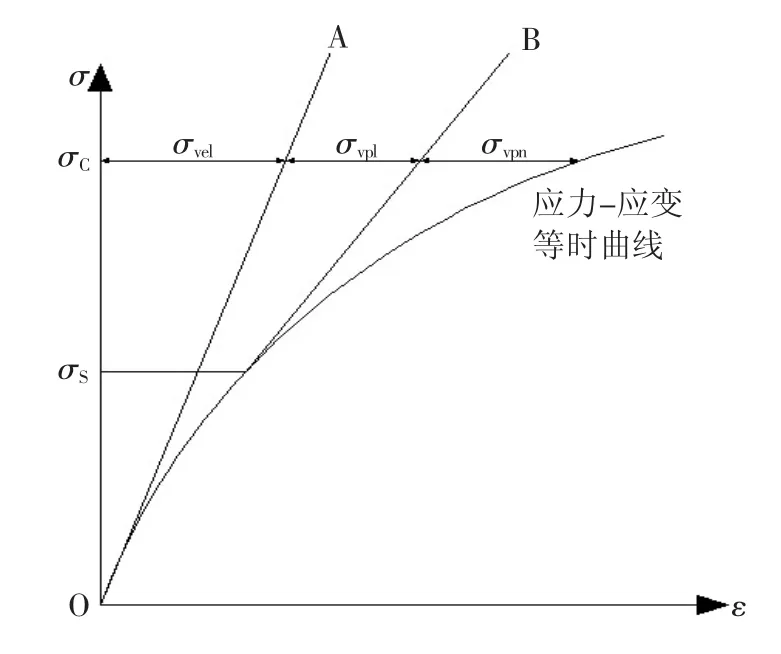
图4 应变的分解
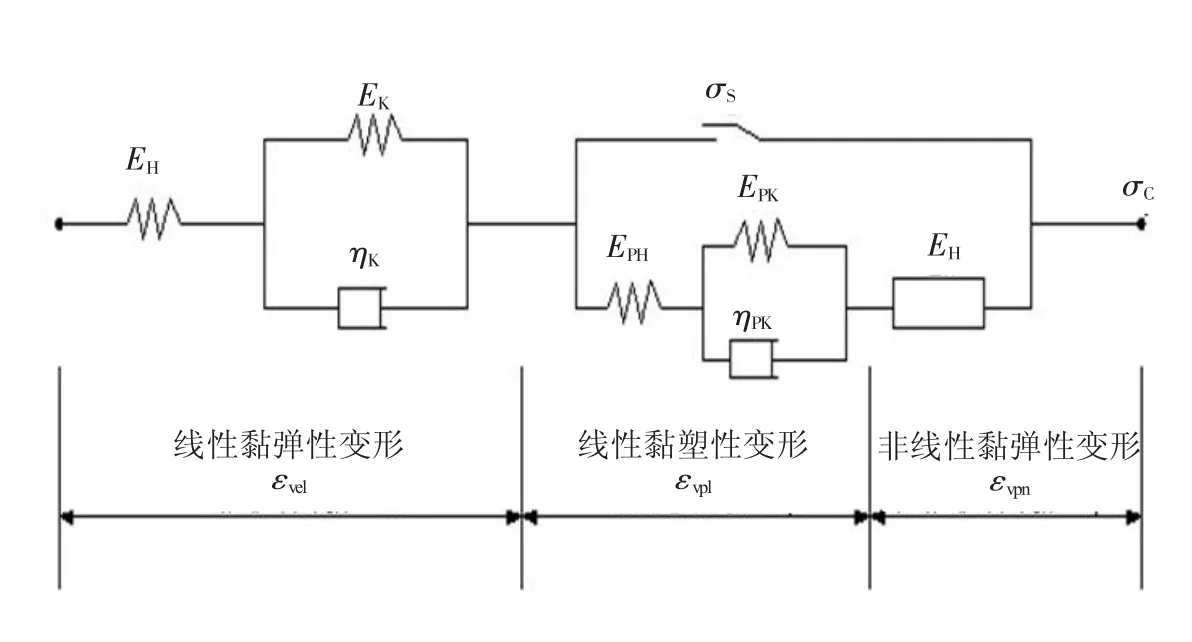
图5 海相沉积软土流变本构模型
3.1 线性黏弹性模型
由图4可知,当应力水平σC小于屈服应力σS时,可将应力—应变等时曲线近似看作直线,过原点O作应力—应变等时曲线的切线OA,切线的斜率代表不同时刻的线性黏弹性模量Ev(elt),其倒数即为线性黏弹性蠕变柔量Jv(elt)。利用试验结果可得不同围压条件下,线性黏弹性蠕变柔量Jv(elt)随时间变化的规律,如图6所示。由图6可知,当t=0时刻线性黏弹性蠕变柔度Jv(elt)有一个初始值,对应t=0单位应力作用下的线性黏弹性应变,随着时间增加蠕变柔度Jv(elt)逐渐增大,但增速随时间逐渐减小,最后趋于稳定值。此时软土蠕变处于衰减稳定阶段,可采用由Kelvin体和虎克弹簧串联而成的Merchant模型进行模拟[19-20],其蠕变方程为
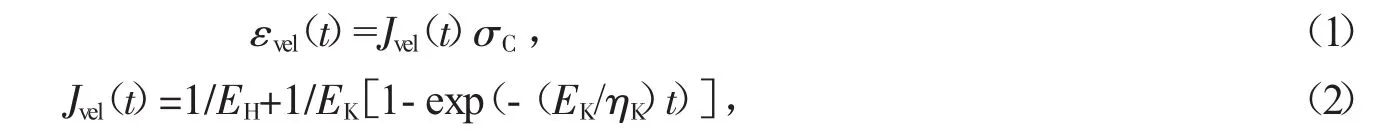
式中,参数EH为虎克体弹簧模量,EK、ηK分别为Kelvin体弹性模量和黏滞系数。
基于图6所示的蠕变试验分析结果,利用公式(2),采用MATLAB编制最小二乘法拟合程序可得不同围压下线性黏弹性蠕变变形参数取值如表2所示。
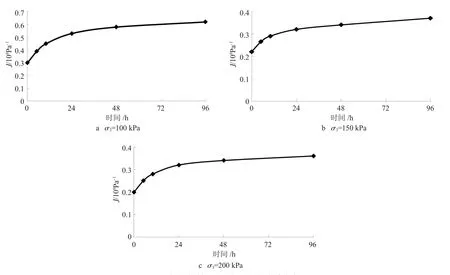
图6 线性黏弹性Jvel(t)与时间的关系曲线
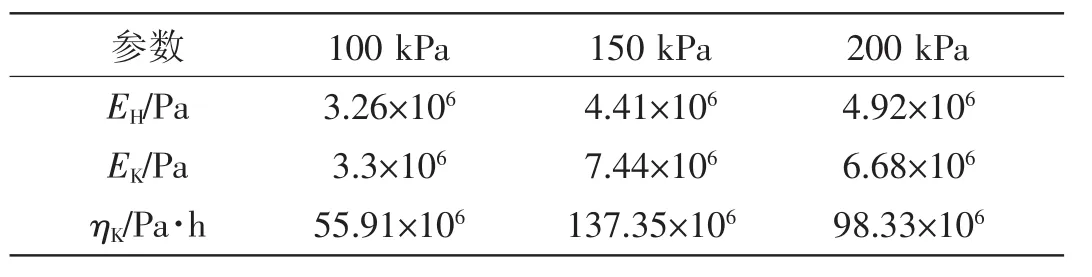
表2 不同围压下线性黏弹性蠕变变形参数
3.2 线性黏塑性模型
如图4所示,过屈服应力σS所对应的点作切线OB,分离出黏塑性应变偏离切线的线性黏塑性应变εvpl,切线斜率即为线性黏塑性模量Evpl(t)。因线性黏塑性蠕变柔度Jvpl(t)与线性黏塑性模量成反比,由此可得Jvpl(t)随时间变化关系,如图7所示。由图7可知,t=0时,线性黏塑性蠕变柔度Jvpl(t)为一个非零初始值,随着时间增加,塑性蠕变柔度Jvpl(t)逐渐增大,但增速逐渐减小,最后趋于稳定值。线性黏塑性应变εvpl随过应力(σC-σS)增大而呈线性增长,假定其比例系数为线性黏塑性蠕变柔度Jvpl(t),则线性黏塑性应变可表示为

线性黏塑性蠕变可以采用摩阻滑块、H-K模型串联的组合模型进行模拟,其蠕变方程为
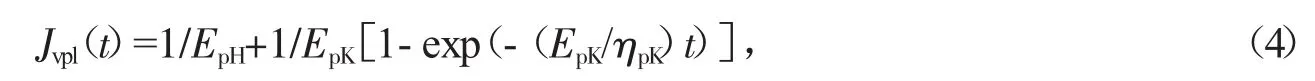
式中,EpH为虎克体弹簧模量;EpK、ηpK分别为Kelvin体弹性模量和黏滞系数。
采用与线性黏弹性模型参数相似的方法,即基于图7所示的蠕变试验分析结果,利用公式(4),采用MATLAB编制最小二乘法拟合程序可得不同围压下线性黏塑性蠕变变形参数取值如表3所示。
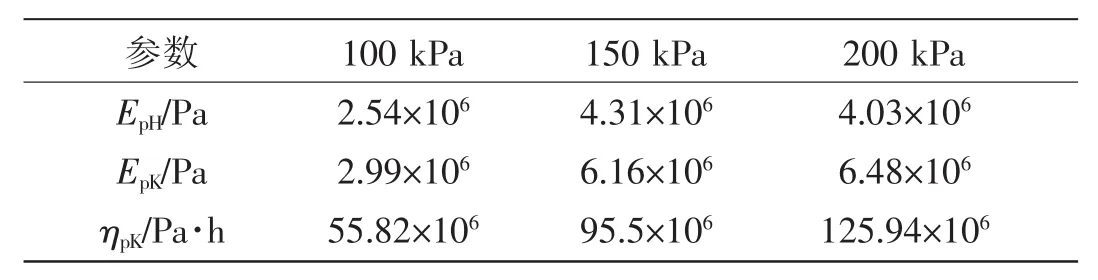
表3 不同围压下线性黏塑性蠕变变形参数
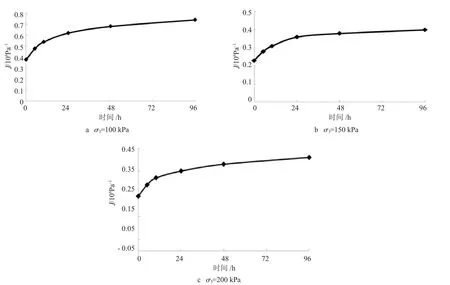
图7 线性黏塑性Jvpl(t)与时间的关系曲线
3.3 非线性黏塑性模型
非线性黏塑性模型采用幂次函数的经验本构模型进行模拟[20-21],即

当t=0时,非线性黏塑性应变并非为零。因此,式(5)不能反映t=0时的非线性黏塑性应变,需要将式(5)增加一个与时间无关的常数项,以使其能够反映t=0时的非线性黏塑性应变,即
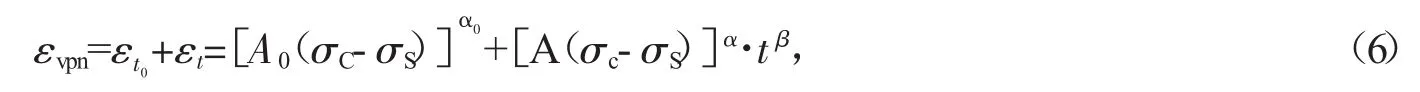
式中,A、A0分别为非线性变形系数;α0、α为硬化系数。
为确定以上参数,对瞬时非线性黏塑性的应变εt0和任意时刻应变εt两边取对数可得
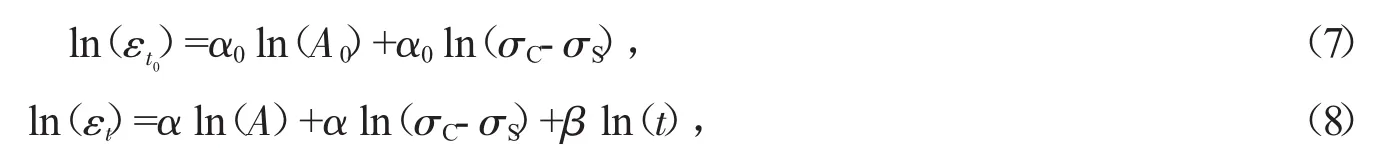
其中,瞬时蠕变指数 α0为 ln(σC-σS)~ln(εt0)的斜率,α0ln(A0)为 ln(σC-σS)轴上的截距;任意时刻蠕变指数 α 为 ln(σC-σS)~ln(εt)的斜率,α ln(A)为ln(σC-σS)轴上的截距,β为ln(t)~ln(εt)的斜率。由试验数据可得围压分别为100 kPa、150 kPa、200 kPa时,非线性黏塑性应变的经验参数,具体取值如表4所示。
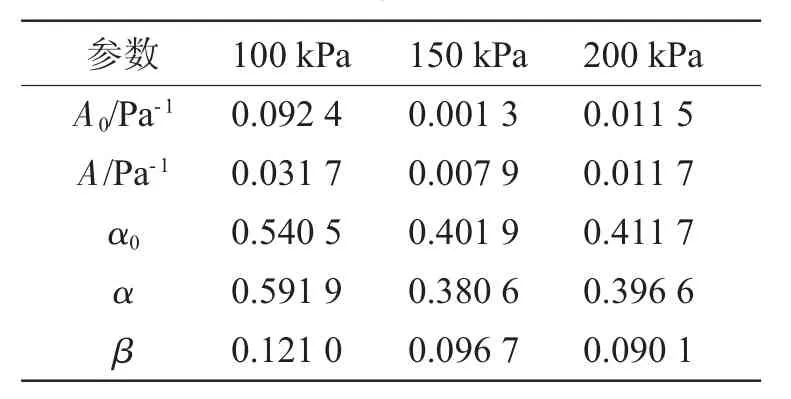
表4 不同围压下非线性黏塑性蠕变变形参数
3.4 流变模型检验
由前述可知,珠三角地区典型软黏土非线性流变本构关系为ε=εvel+εvpl+εvpn。将不同围压条件下,由流变模型拟合而成的蠕变曲线以及试验蠕变曲线描绘在同一坐标系,如图8所示。由图8可知,试验结果与模拟曲线非常吻合,表明图1所示的组合本构模型可较好地模拟珠三角地区海相沉积软粘土的蠕变变形特性。
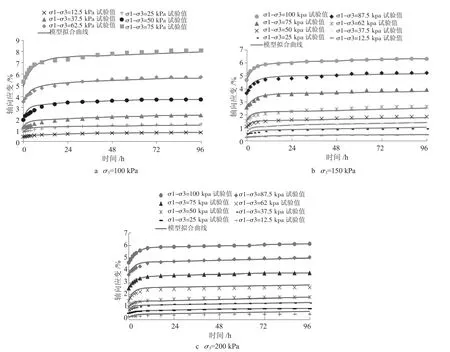
图8 流变模型模拟结果
4 结论
(1)珠三角地区典型海相沉积软粘土具体显著的非线性蠕变特性,采用线性黏弹性模型、线性黏塑性模型和非线性黏塑性模型串联而成组合模型,并基于MATLAB最小二乘法拟合得到模型参数,可较好地模拟其蠕变变形特性。
(2)海相沉积软粘土的蠕变特性与其所受到的围压有关,当偏差应力水平相同时,围压越大,试件瞬时变形和蠕变变形量越小,试件破坏所对应的偏差应力水平越高,而破坏时所产生的轴向应变越小。
(3)在较低偏差应力水平下,蠕变速率随时间的增加而减小,最终趋于稳定值,软土蠕变表现为稳定性衰减蠕变,在较高偏差应力水平下,因结构性遭到破坏,软土蠕变表现为非稳定性衰减蠕变或加速蠕变。
(4)基于大尺寸三轴蠕变试验方法开展软土流变特性研究,可为珠三角地区软土路基工程以及地下工程时空效应分析提供可靠试验依据,对完善软土路基以及地下工程设计和施工理论具有重要的现实意义。
