Spin Thermoelectric Effects in a Three-Terminal Double-Dot Interferometer∗

Feng Liang(梁峰), Ben-Ling Gao(高本领),Guang Song(宋光),and Yu Gu(古宇)

1Department of Applied Physics,Huaiyin Institute of Technology,Huaian 223003,China

2Department of Physics and Siyuan Laboratory,Jinan University,Guangzhou 510632,China

AbstractWe theoretically investigate the thermoelectric properties of a three-terminal double-dot interferometer with Rashba spin-orbit interaction.It is found that with some temperature distributions a thermal spin current can even be produced without the help of magnetic flux and by tuning the spin interference effect in the system,a pure spin or fully spin-polarized current can be driven by temperature differences.For the cases that two of the terminals are held at the same temperature,the charge(spin)thermopower and the charge(spin) figure of merit are defined and calculated in the linear response regime.With some choices of the system parameters the calculated spin and charge thermopowers are of the same order of magnitude and the charge figure of merit can exceed 1.

Key words:thermoelectric effects,thermal spin current,Rashba spin-orbit interaction,interferometer,nonequilibrium Green’s function method

1 Introduction

During the last few years,a new sub field of spintronics named as thermospintronics[1−2](or spin caloritronics)has emerged in condensed matter physics.To realize the functionalities of thermospintronics devices,a variety of efforts from both theoretical and experimental areas have been devoted to investigate how to generate a spin current by means of the temperature difference instead of the electric voltage bias.The findings of the spin-dependent thermoelectric effects in various materials and nanostructures have paved the way for the realization of thermally driven spin-polarized transport through solid state devices.A pioneering work about this was an experimental one[3]that demonstrated the possibility of generating a longitudinal spin current in the permalloy NiFe by using a temperature difference.After then,this phenomenon which is often referred to as the spin Seebeck effect was also observed in a ferromagnetic semiconductor system,[4]in thin films of the Heusler compound Co2MnSi[5]and even in magnetic tunneling junctions.[6−8]In addition to the spin Seebeck effect,the thermospin effect in quantum dot(QD)systems[9−16]and the spin-dependent Seebeck effect in Aharonov-Bohm interferometers[17−22]have also attracted a great amount of attention.For instance,Gong et al.[9]proposed that an apparent thermospin effect can occur in a quantum dot system under the action of circularly polarized light.This effect originates from the spin polarization induced by the polarized light.Up to now,the Aharonov-Bohm interferometers for research of the spindependent Seebeck effect are mostly two-terminal ones.Due to the phase locking effect,[23]driving a spin current to flow through such a system must require the help of magnetic materials or magnetic flux.However,a threeterminal interferometer can get rid of this effect and in fact it has been demonstrated that in three-terminal quantum interferometers a spin-polarized current can be produced purely by electric voltage or temperature bias.[24−28]

Inspired by the previous works about the spinpolarized electron transport in three-terminal mesoscopic interferometers,[24−28]the spin-dependent thermoelectric effect in a three-terminal double-dot interferometer,in which the Rashba spin-orbit interaction(RSOI)is considered in one of the QDs,is investigated in this work.Due to the spin-dependent quantum interference effect based on the RSOI,temperature differences applied to the system can also give rise to a spin current.By using the nonequilibrium Green’s function method,we studied the properties of the generated thermal spin current in detail and demonstrated the controllability of the thermoelectric and thermospin transport processes in the studied system.The rest of the paper is organized as follows.In Sec.2,a model Hamiltonian for the studied system is given and the general formalism for the thermal spin current,the charge(spin)Seebeck coefficient and the charge(spin) figure of merit are derived.In Sec.3,the numerical investigation is presented to show the properties of the thermoelectric and thermospin transport in the mesoscopic interferometer.Finally,a brief conclusion is drawn in Sec.4.

2 Model and Method

In this paper we investigate a thermospin device consisting of two single-level QDs,which are coupled to three normal leads as displayed schematically in Fig.1.The left and right leads are coupled to both of the two QDs,but the middle lead is only coupled to QD2.A magnetic flux Φ may penetrate through the area enclosed by this device and the RSOI is only taken into account in QD1.Using the method of second quantization,the studied three terminal mesoscopic interferometer can be described by the following Hamiltonian

The term HCin Eq.(1)is the Hamiltonian for electrons in the three normal leads.With the free electron gas model,HCcan be written as

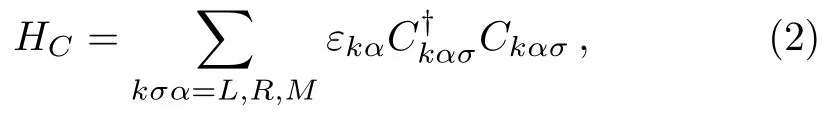
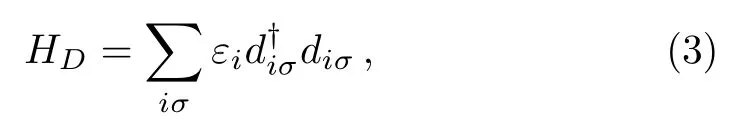
In the above equation,the tunnel matrix element tαiσis assumed to be independent of momentum k and it can be written asThe spin-dependent phase factor φσcan be described as φσ= ϕ − σφ,in which the Aharonov-Bohm(AB)phase ϕ =2πΦ/Φ0with Φ0being the flux quantum and the RSOI-induced spin precession phasewith α being the RSOI strength,L being the length of QD1,and m∗being the electron effective mass.

In this work,we only focus on the electron transport in the middle lead.By employing the nonequilibrium Green’s function method,the spin-dependent electric current in the middle lead in stationary state can be expressed in the general Landauer-Büttiker formula form[30−31]

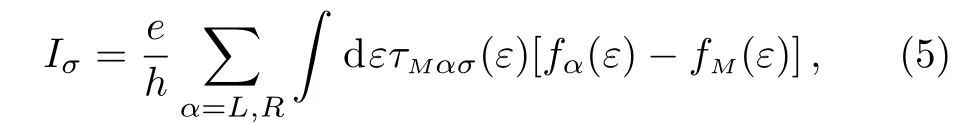
For simplicity,the tunnel couplings between the QDs and the leads are assumed identical withand Γ = πt2ραwhere ραis the density of electron states in lead α.In the expression of the transmission coefficient,anddenote the spin-dependent retarded and advanced Green’s functions of the QDs in the spectrum space respectively which satisfy the relationFollowing from the Dyson equation,the retarded QDs Green’s function can be calculated as

where the bare QDs Green’s functioncan be obtained by the equation of motion method

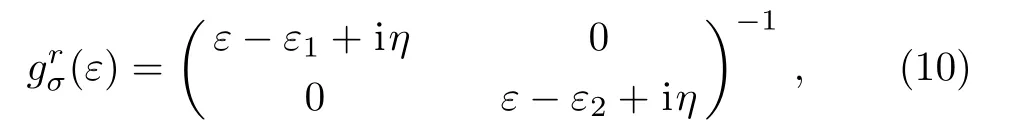
with η being a positive infinitesimal and within the wideband approximation the self-energy contributed by the three leads is written as∑(α =L,R,M).After some straightforward algebra calculations,we get

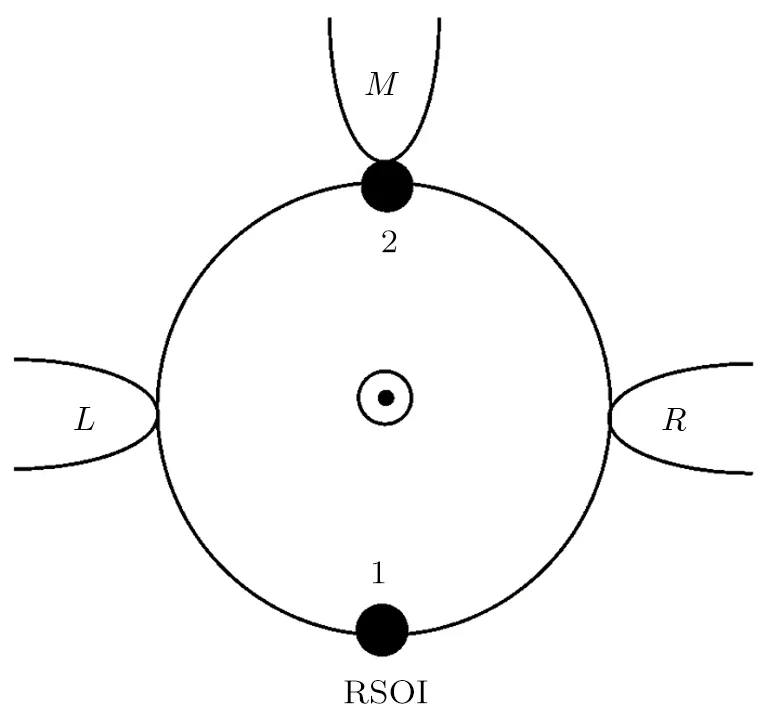
Fig.1 Schematic plot of a three-terminal double-dot interferometer,in which a QD contains RSOI.A magnetic flux may penetrate the area enclosed by the ring-shaped system.

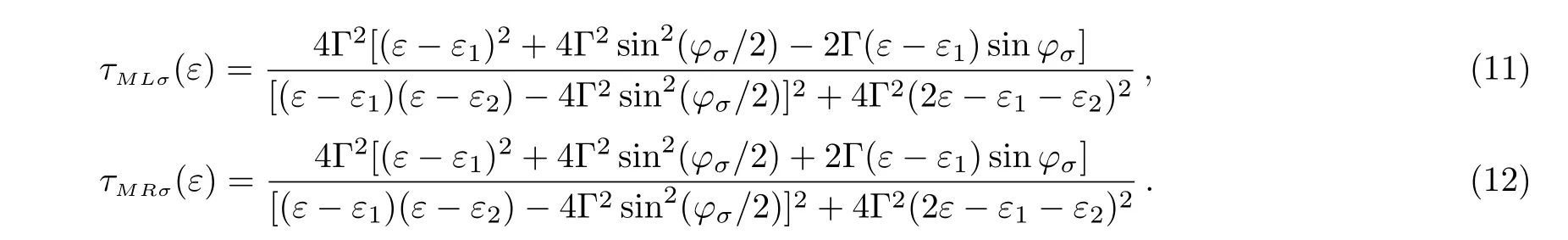
To investigate the influence of the temperature distribution on the spin-dependent thermoelectric transport properties of the system qualitatively,we focus on the three cases forandThe case ofis similar with the case of,so it is not specially discussed in this paper.For the case of,due toEq.(5)can be reduced to

with

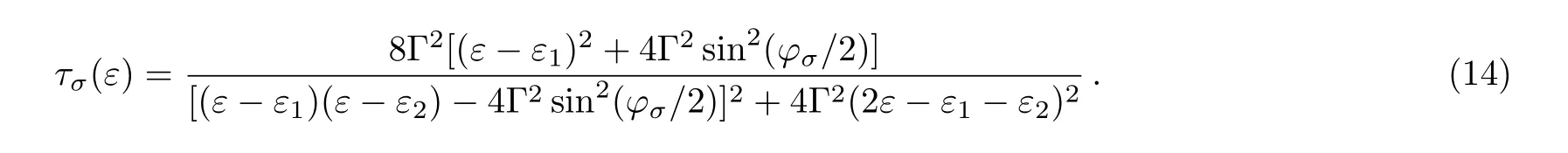
3 Results and Discussions

For numerical calculations,the dot-lead coupling strength Γ is assumed to be the energy unit,i.e.,Γ =1.The common chemical potential of the three leads is taken as the energy reference and the dot energy level in QD1 is set to be aligned with it,i.e.,µL= µR= µM= ε1=0.

In Fig.2 we show the thermally driven charge current Icand spin current Isas functions of the dot energy level ε2for the case ofAs we have discussed above,in this situation only if the RSOI is present in the system a spin current can be generated to flow through the middle lead by temperature differences even without any magnetic flux.So as shown in Fig.2(a)in addition to a charge current a spin current also varies with ε2for ϕ =0.But the charge current and spin current possess different symmetries.To be exact,the charge current satisfies the symmetrywhile the spin current satisfies the symmetryTo understand this difference,we define ταc, ταsand∆fαasand.Then according to Eq.(5)and the relevant definitions,the charge and spin currents have the forms

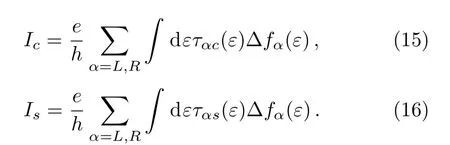
It is easy to demonstrate that

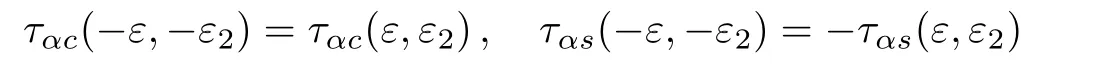
when ϕ =nπ(n=0,1,2,3,...).These symmetries together with the fact that

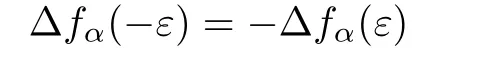
lead to the integration on the right side of Eq.(15)(and thus Ic)and Eq.(16)(and thus Is)having centrosymmetry and mirror symmetry about ε2=0 respectively for ϕ =0(see Fig.2(a))and ϕ = π (see Fig.2(d)).When the phase ϕ lies between 0 and π,the relationsandcannot hold ever so that the charge and spin currents loose their original symmetries(see Figs.2(b)and 2(c)).The sign of the spin current can also be changed with the variation of ϕ. Compared to the sign of the spin current in the case of ϕ=0,the sign of the spin current in the case of ϕ = π is completely reversed.This is because the sign of ταsis reversed under the operation ϕ → ϕ + π.But ταcremains unchanged under this operation and thus so does the charge current.In Fig.2,at some points(A1,A2,A3,A4)the charge current completely vanishes while the spin current is nonzero.Thus by tuning the system parameters appropriately a thermally driven pure spin current can be produced in the proposed device.Moreover,the formation of the pure spin current at point A1also implies that the proposed device can act as an all-electrical pure-spin-current thermal generator since the magnetic flux is absent in Fig.2(a)and the dot energy level ε2can be tuned by a gate voltage.At some other points(B1,B2,B3,B4)the charge current is identical with the spin current indicating that a fully spin-polarized charge current,which is composed of only one spin component current,can also be thermally driven to flow in the middle lead.

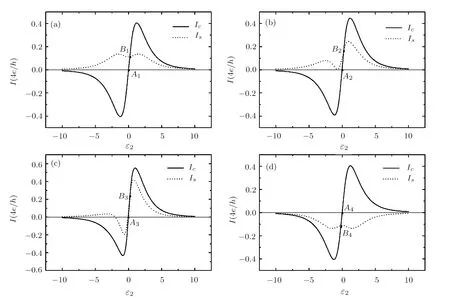
Fig.2 The thermally driven charge and spin currents versus ε2for(a)ϕ =0,(b)ϕ =0.1π.(c)ϕ =0.25π and(d)ϕ = π.Other parameters are chosen as ϕ =0,kBTL=1.0,kBTR=0.5,and kBTM=0.1.

The RSOI induced spin-dependent quantum interference effect should play a crucial role in the generation of the spin current.To show this clearly,in Fig.3 we plot the spin current as a function of the RSOI-induced phase φ with different values of the dot-lead coupling strength Γ forand ϕ =0.The numerical results show that the spin current oscillates as a function of φ with a period of 2π.For weak dot-lead coupling,the spin current is a perfect sinusoidal function.However,with the increase of the dot-lead coupling strength the spin current exhibits a non-sinusoidal oscillation.We can explain this as a result of the spin interference effect between different Feynman paths.For the studied device,there are two possible paths for an electron tunneling from the αth lead to the middle lead.One path is the αth lead → QD1→ the βthlead → QD2 → the middle lead and the other one is the αth lead → QD2 → the middle lead.As the dot-lead coupling is weak,one can only consider the lowest-order tunneling process,the spin-dependent effective coupling strength between the αth lead and the middle lead can be expressed as[27−28,32−33]

Obviously when ϕ=0,sinφσ=σ sinφ and thussinφ such that the thermally driven spin current flowing in the middle lead behaves like a sinusoidal function.On the contrary,for the strong coupling case the contribution from higher-order tunneling processes is not negligible,which causes the difference between the two spin-dependent effective coupling strength never to be proportional to sinφ and consequently leads to the deviation of the spin current from a sinusoidal function of φ.

Fig.3 The thermally driven spin current versus φ for ϕ =0, ε2=1.0,kBTL=1.0,kBTR=0.5,and kBTM=0.1.

Equation(18)shows a linear relation between the spindependent current Iσand the temperature difference in the linear response regime,which induces the charge(spin)current to be linear functions of kB∆T(see Fig.4(c)).Asthe temperature difference is defined by∆T=TR−TM.From Eq.(5)the spin-dependent current in the middle lead for this case can be expressed as

Utilizing the same approximation method as adopted above,Eq.(19)yields

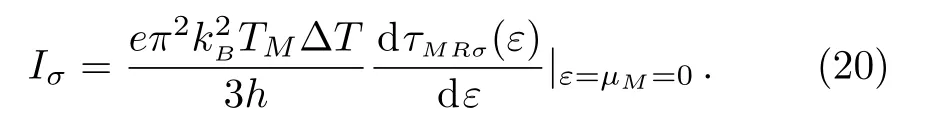
As a result,the charge and spin currents for the case ofare also linear with kB∆T(see Fig.4(d))when the temperature difference is considerably small(kB∆T≤0.5).

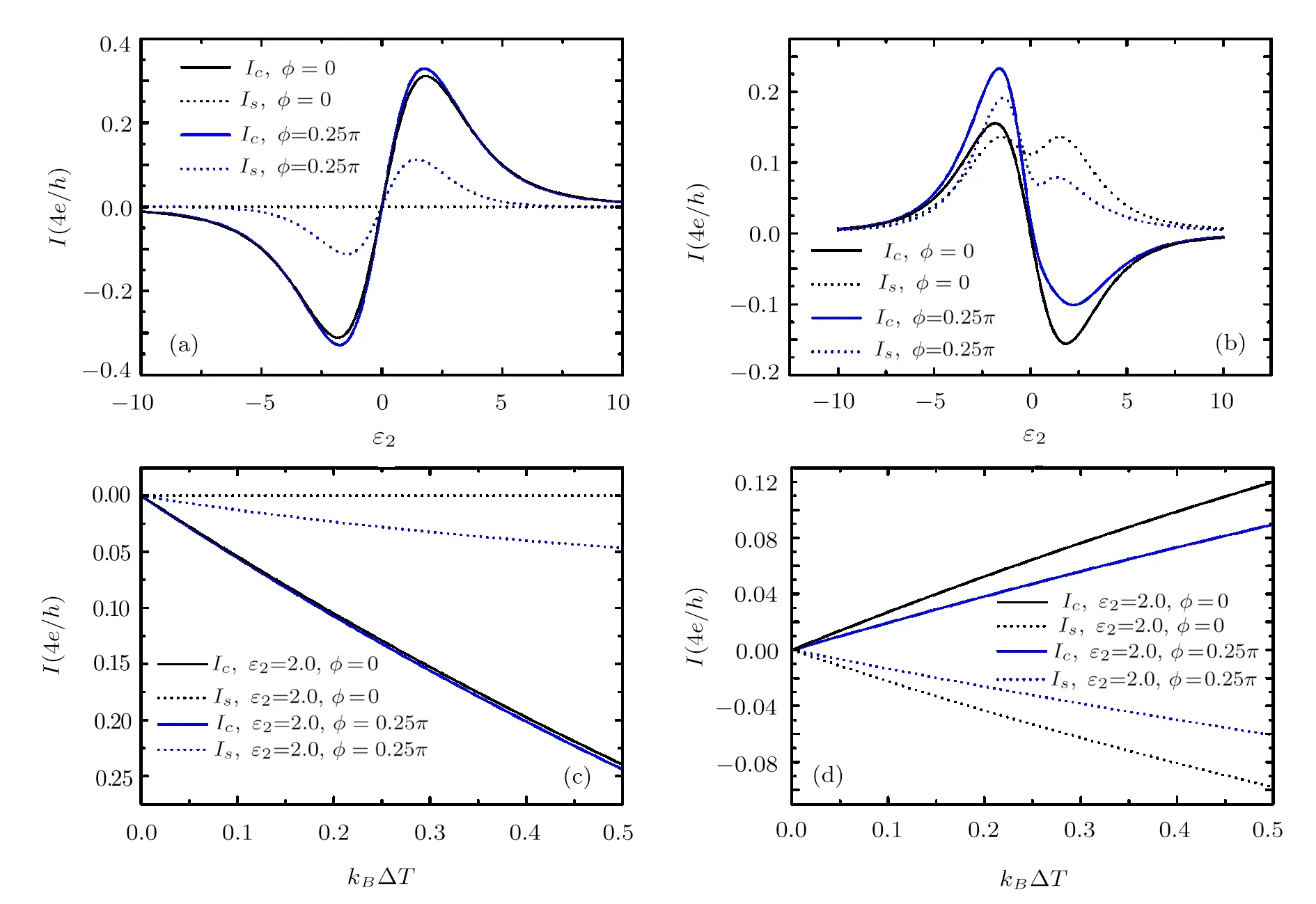
Fig.4 (Color online)The thermally driven charge and spin currents versus ε2for(a)kBTL=kBTR=1.0 and kBTM=0.5 and(b)kBTL=kBTM=1.0 and kBTR=0.5.The thermally driven charge and spin currents versus kB∆T for(c)and(d)The spin precession phase is set as ϕ =0.

Fig.5 (a)The charge and spin thermopowers versus ε2.(b)The charge and spin figure of merits versus ε2.(c)The ratioat ε=µL=0 versus ε2.The other parameters are chosen as kBTL=kBTR=1.0,kBTM=0.5,ϕ =0.25π,and ϕ =0.

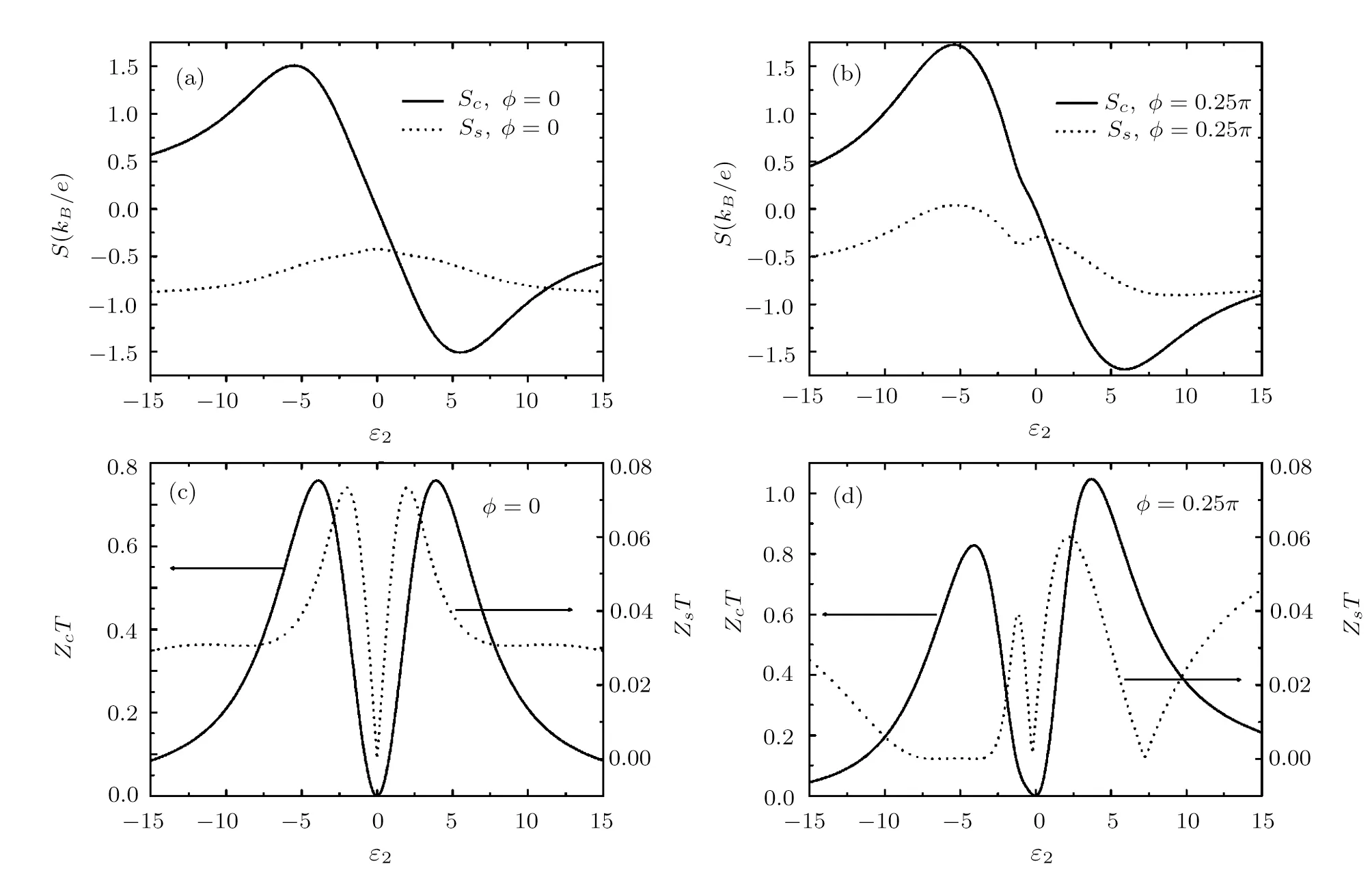
Fig.6(a)and(b)The charge and spin thermopowers versus ε2.(c)and(d)The charge and spin figure of merits versus ε2.The other parameters are chosen as kBTL=kBTM=1.0,kBTR=0.5,and ϕ =0.

4 Conclusion

In conclusion,we have explored the thermoelectric and thermospin transport in a three-terminal double-dot interferometer with one dot containing RSOI.The results evaluated by the non-equilibrium Green’s function technique show that some particular temperature distribution makes the generation of the thermal spin current demand the help of a magnetic flux.However,at other temperature distributions the magnetic flux is not indispensable for producing the spin current thermally.By appropriately adjusting the system parameters,the proposed device can work as a pure-spin-current or fully-spin-polarized-current thermal generator.For other two cases that only one terminal is kept at a temperature different from the others,the system under study resembles a two-terminal device,the defined spin thermopower is shown to be comparable to the charge one and the defined charge figure of merit is expected to exceed 1.These characteristics of the currents,thermopowers and figure of merits endow the considered setup with potential application values.Furthermore,some other interesting properties of the currents,thermopowers and figure of merits are also revealed in this paper.