锚索测力计偏心受压情况下的误差分析

张才连，冯 波

（1．浏阳市水务局，湖南 长沙 410300；2．南京卡尔胜水电科技有限公司，江苏 南京 210012）

预应力锚索由于加固深度大、加固力强，施工效率高等特性，在岩质边坡加固工程中有非常广泛的应用。在重要边坡的加固过程中，通常会选择一定比例的典型锚索安装锚索测力计，监测锚索张力的变化，以便对加固效果进行长期的监测，为边坡的稳定分析提供必要的数据支撑。众多资料和实际施工经验表明锚索测力计在锚索张拉、锁定过程中测到的张力与按千斤顶油压计算出来的张力有较大的差异，有时甚至超过20%。不少学者对造成这种差异的原因进行了分析，多数认为锚索的施工质量不好，锚索钻孔的中心线与锚索测力计的轴线不重合是造成这种误差的主要原因，也就是说锚索测力计是在偏心受压的状态下工作。由于锚索钻孔不可能完全顺直，如果借用钻孔有效圆的概念就是说由于钻孔的弯曲造成有效圆的孔径小于锚索钻孔孔径，就算有较大的有效圆，有效圆内能够容下一台锚索所有的钢绞线，但由于钢绞线的性质，在下索后对底部进行灌浆锚固时也不能保证都将锚索均匀锚固在有效圆内。因此锚索测力计在偏心受压状态下工作是普遍存在的现象。本文从使用最广泛的振弦式锚索测力计的结构出发，研究锚索测力计在偏心受压情况下的状态，通过必要的试验进行分析，希望找到这种误差最主要的原因，以便于指导锚索的施工。

1 振弦式锚索测力计校验与理论值对比

（1）锚索测力计校验。振弦式锚索测力计多数情况为4弦，结构图如图1所示，4根弦均匀布置在承压环侧面，当承压环受轴向压力产生变形时，弦的变形与承压环的变形满足变形相容条件，也即应变相同，从而引起钢弦自振频率的变化，可以建立钢弦自振频率与承压环轴向力之间的关系。这样可以通过测量钢弦自动频率的变化来计算承压环轴向力的变化，这是锚索测力计的测量原理。

锚索在张拉过程中当测力计实测值与按千斤顶压力的计算值存在较大误差时，有不少人认为是锚索测力计测量不准确，笔者不认同这种观点，曾对10台2000 kN的锚索测力计进行过复核，复核采取的线路如下。

（2）先在压力试验机上对锚索测力计进行精确标定，得到锚索测力计在各级荷载下的频率，从而可建立荷载与频率之间的关系，这也是锚索测力计最主要的出厂检验资料。

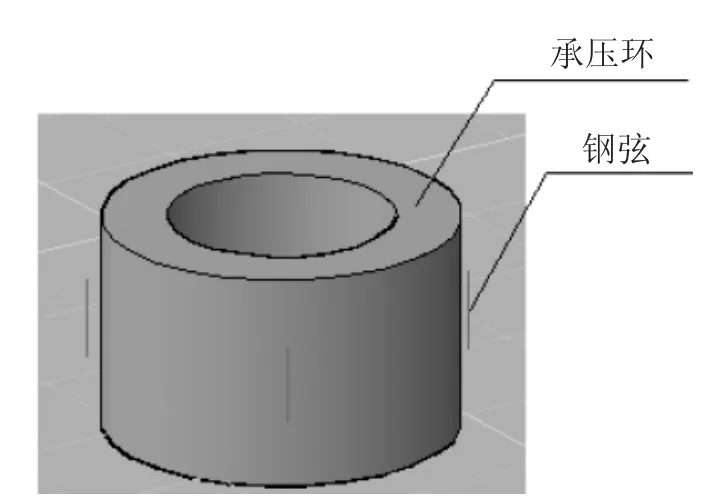
图1

（3）从上述试验得到锚索测力计的频率后，从锚索测力计的结构出发，按变形相容条件反算荷载，探求计算荷载与实际荷载之间的差异。

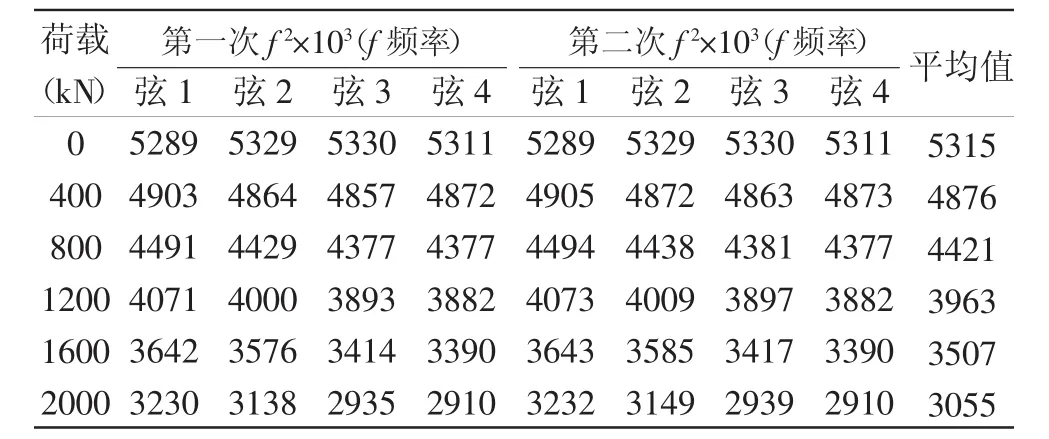
表1 锚索测力计标定资料

由上述标定可得到该锚索测力计荷载的计算公式为：

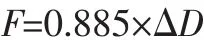
式中：F—荷载，kN；ΔD—频模的变化量。

（4）锚索测力计理论值计算。由于锚索测力计承压环和钢弦均在线弹性范围内工作，因此对承压环满足以下的关系：

式中：ε—承压环应变；E′—承压环弹性模量，Pa；F—承压环荷载，N；A—承压环受力面积，m2。

钢弦的自振频率公式为：

由（2）可以得到钢弦的应变为：

式中：L—钢弦的长度，m；ρ—钢弦的密度，kg/m3；f—钢弦自振频率，Hz；E—钢弦弹性模量，Pa。

根据变形相容条件，由（1）、（3）不难得到锚索测力计荷载的变化量与钢弦频率的变化之间的关系如下：

式中：ΔF—荷载变化量，N；f0—零荷载下的钢弦频率，Hz；f—某级荷载下的钢弦频率，Hz。

按（4）式计算表1中的荷载，并与实际输入荷载对比，结果如下表2所示。其中取E′=E，ρ=7850 kg/m3，钢弦的长度为锚索测力计的关键设计参数，此锚索测力计弦长L=53.00 mm，承压环内径95.00平共处mm，外径148.00 mm，高度120 m，均取f0和f的平均值。

表2 锚索测力计理论计算荷载与实际荷载对比

由上表可知，按钢弦与承压环变形相容条件及锚索测力计结构参数计算出来的理论荷载与实际荷载的误差最大为2.08%，这个误差是可以接受的。这也说明正规厂家生产的锚索测力计经出厂标定以后，其测值是比较准确的，不是锚索施工过程中测力计测量值与按张拉千斤顶计算值误差较大的主要原因。

藻细胞周边的水分由于受到藻细胞的束缚，其性质和未受到束缚作用的自由水有差别。藻泥中的水可被分为2种：由于藻细胞固体物质的存在导致其性质发生变化的束缚水和性质不受固体物质影响的自由水［12］。含水物质（如市政污泥）中的束缚水不能通过传统的脱水方法（如离心、絮凝或过滤）被脱除。

2 锚索测力计偏心受压时受力分析

锚索测力计的偏心受压有两种典型的工况：（1）锚索张紧后的合力与锚索测力计的轴线平行，但存在偏心距e；（2）锚索的合力与锚索测力计轴线存在夹角，如下图所示。

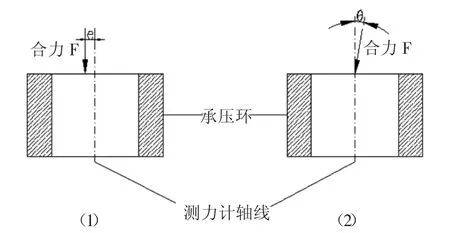
图2 锚索测力计两种典型工况

锚索测力计在工作时，多数情况是上述两种工况的组合，为便于分析问题，对上述两种工况单独进行分析。

3 存在偏心距e时的误差分析

对于第一种情况，采用在压力试验机上人为设置偏心距的方式进行分析（试验时设计了压力试验机与锚索测力计配合的传力块，便于设置偏心距），偏心距分别设置为2、5、10 mm，如下图 3所示。

测试用的锚索测力计仍然采用上述型号的锚索测力计，每个测试档位计算锚索测力计的计算值与压力机实际值之间的误差（锚索测力计计算时基准值试验开始前选取，试验温度保持不变），统计如下表3示。

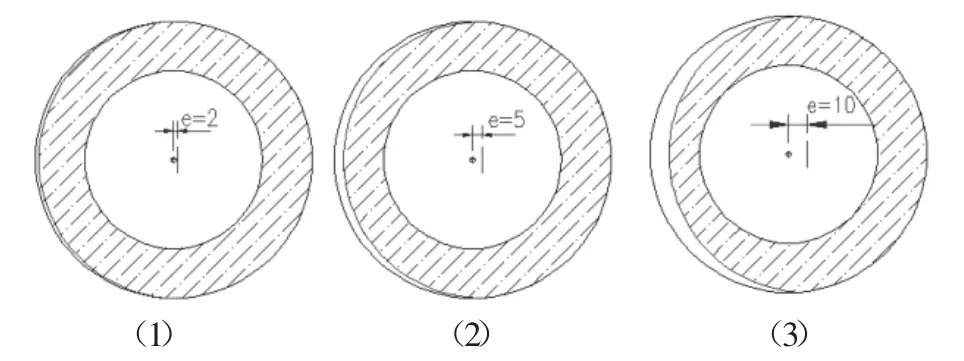
图3 锚索测力计偏心受压试验示意图

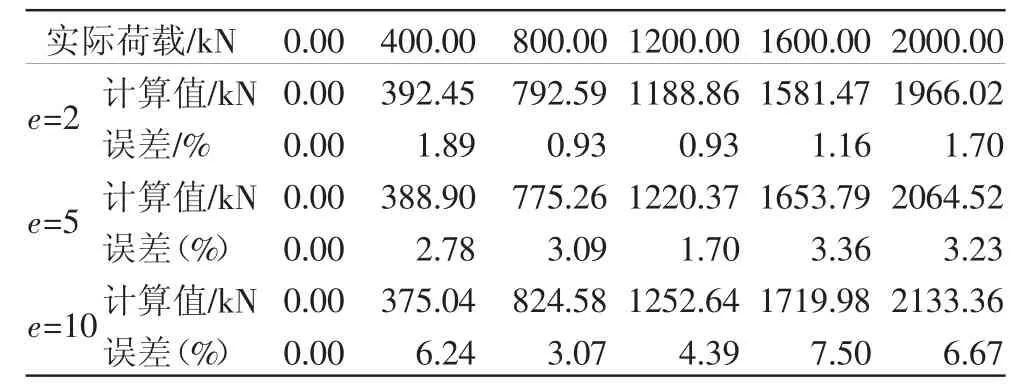
表3 锚索测力计偏心受压时测量误差统计表

由表3可知，对于试验的锚索测力计，在第一种偏心受压情况下，在试验室3种试验工况下最大误差为7.50%，这是在试验室情况下，压力机的压力通过传力块比较均匀地传到图2锚索测力计的阴影面积上，实际上在施工现场，工作锚的传力情况不可能有这么好，因此在同等的偏心距下，现场的测量误差可能还要大于本试验得到的误差水平。

锚索测力计在现场张拉过程中，容易保证工作锚与测力计的同轴度，但偏心距存在的主要原因并不是保证同心度就可以避免。我们知道钢绞线张力通过工作锚将力传递到锚索测力计上，钢绞线在工作锚上是对称分布的，但由于每根钢绞线上的张力不可能完全保持一样，这样对锚索测力计承压环而言就产生了偏心受压，同时受到弯矩的作用，产生测量误差。

4 存在偏心角θ时的误差分析

当存在偏心角θ时，由于荷载较大，不好在实验室模拟，因此拟用数值计算的方法进行分析。分析线路如下：

（1）建立有限单元模型，荷载以面力施加在承压环上，荷载与承压环法线方向的夹角为θ。

（3）由公式（3）理论计算弦在上述应变变化量时对应的频率变化量。

（4）对4根弦的变化量取平均值，代入锚索测力计厂家的计算公式，求得锚索测力计的计算荷载，并与建模时施加的荷载进行比较，分析误差范围。

数值计算时仍采用上述型号的锚索测力计建模，偏心角 θ分别取 θ=1°，θ=3°，θ=5°，荷载 Q 分别取 500、1000、1500、2000 kN（荷载转换成面力进行加载），对计算结果按上述（2）（3）（4）步骤进行分析，统计结果如表 4 所示。

由表4可知，从数值计算的结果来看，存在偏心角θ时，对锚索测力计的影响很大，偏心角越大测量误差越大，当偏心角为5°时，最大误差达到11.67%。虽然这是数值计算的结果，模型不能完全模拟现场实际情况，但也可以说明，偏心角是造成测量误差非常重要的原因，实际施工过程中应尽量减小偏心角，必要的时候可以检验锚垫板与钻孔之间的夹角（锚垫板法线与钻孔轴线方向的夹角即为偏心角）。

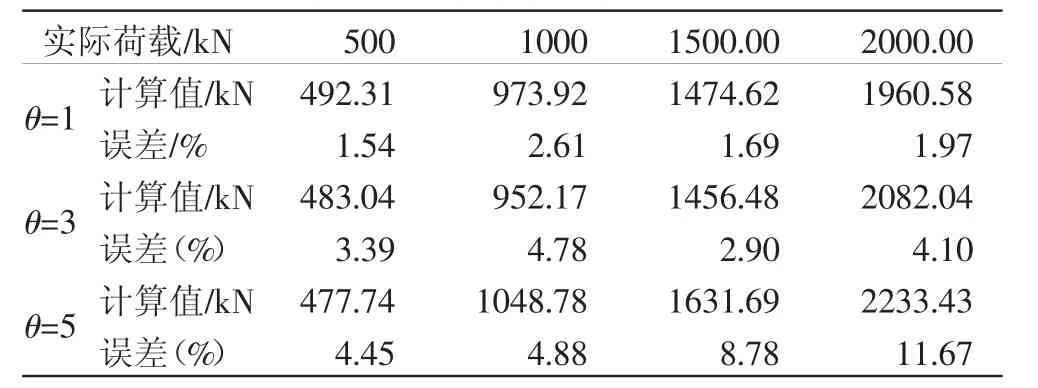
表4 锚索测力计存在偏心角时误差统计表

5 结语

锚索测力计是边坡、地下洞室加固过程中用得比较多的监测仪器，在施工过程中对锚索测力计测值与按张拉设备计算出来的测值之间的误差也有不少文献进行了分析，本文通过试验和数值计算分析认为，对于合格的锚索测力计在压力试验机上良好加载时，其测量值没有大的误差。当荷载存在偏心距或偏心角时其最终荷载误差明显过大，在这两种情况下，锚索测力计承压环的受力都不均匀，可能有部分承压环内力已经超过了材料的弹性极限，产生了塑性变形，承压环的应力与应变之间已经不是线性关系所致。要减小锚索测力计的测量误差，可以从以下两方面考虑：

（1）锚索测力计生产厂家在设计锚索测力时，承压环材料应该完全在线弹性范围内工作，当达到设计荷载时，承压环材料的弹性极限应该还有一定的余度，笔者认为不应小于20%，以避免偏心受压时承压环部分屈服，造成很大的测量误差。

（2）偏心距和偏心角的存在是锚索测力计误差的主要来源，应该做到钻孔平直，钻孔有效圆面积大，另外锚垫板外平面与钻孔的垂直度是关键的控制因素，必要的时候需要进行测定，减小偏心角θ。张拉过程中，各级应张拉均匀，使每束锚索受力均匀，减小合力的偏心距。