多云存储中保护隐私的数据完整性验证方案

2018-11-17任孟琦庞晓琼王田琪聂梦飞

计算机工程与应用 2018年22期

任孟琦，庞晓琼，王田琪，聂梦飞

中北大学大数据学院，太原 030051

1 引言

随着云计算的蓬勃发展，为海量数据提供云服务的云存储系统成为关注热点。用户将数据交由云服务提供商管理，能够有效减轻本地存储负担。然而，云存储[1]是一把双刃剑，它在为用户提供便利的同时也引发了安全性挑战，不可信云服务提供商会为了自身利益而隐瞒用户数据的丢失或损坏，造成数据的完整性破坏。因此，数据完整性验证技术成为云存储中保证数据安全的重要手段。

早期，Ateniese等人[2]提出数据持有性（Provable Data Possess，PDP）模型来验证云存储数据的完整性。模型中，用户通过概率抽查的方式发起对远端服务器的挑战，服务器返回与挑战相关的文件块和数据标签证明回应挑战，并由用户根据回应判断数据的完整性。之后出现了很多在此模型上拓展应用的数据完整性验证方案[3-5]，其中支持公开校验成为数据完整性验证的重要应用拓展，解决了用户作为审计个体计算能力有限的弊端。Wang等人[6]首次引入第三方审计（Third Party Auditor，TPA），提出支持公开审计的PDP方案。TPA的出现减轻了用户的计算负担，同时也带来了新的安全风险。审计过程中，TPA出于好奇可能与服务器进行多次交互从而获得用户数据的相关信息，造成用户的数据隐私泄露[7-8]。Hao等人[9]首次提出“针对TPA隐私性”的概念，并给出了可证明安全的PDP方案。Yu等人[10]在Hao等人基础上加强了方案的隐私性保护并进行了安全证明。文献[11]中Yu等人又提出了一种基于身份的支持完美隐私保护的数据完整性验证方案。目前，支持隐私保护的数据完整性验证方案已成为热门研究课题。

然而，上述方案大多在单用户单服务器环境下提出，如果简单地在多用户多服务器环境下拓展，则使方案效率十分低下。也曾有学者在多云服务器环境下针对方案的隐私性和效率进行了研究，但方案被指出存在安全性攻击。Zhu等人[12]提出多云协同存储并支持隐私保护的PDP模型，但方案被指出存在恶意云服务器攻击的威胁。He等人[13]构造了一个多用户多服务器环境下支持批量审计的PDP方案，但方案缺乏对服务器的安全性证明。Wang[14]提出基于身份的分布式存储PDP方案，该方案也被指出存在恶意服务器方欺骗的安全性问题。

针对上述问题，本文提出一种在多用户多服务器环境下支持批处理校验，同时保护用户数据隐私且针对服务器安全的数据完整性验证方案IDB-RDIC。

本文的创新点：所提方案对多用户多服务器环境下的数据支持高效的批处理校验，与可在多用户多服务器环境下简单拓展的方案[11]相比，降低了TPA和服务器端的通信开销与计算开销。同时本文方案还实现了针对TPA的隐私保护，并对服务器的安全性进行了证明。

2 IDB-RDIC结构模型和安全模型

2.1 结构模型

单用户单服务器环境下的数据完整性验证方案[11]可以简单地在多用户多服务器环境下拓展，拓展之后的结构模型图如图1所示。模型由四类实体构成，当多个用户向第三方TPA发送审计请求任务时，TPA只能为每位用户逐一校验其数据的完整性，由此带来极大的通信与计算开销。

图1 简单的多用户多云存储模型图

为了提高效率，本文方案支持对存储在多个云服务器上的多用户进行批处理校验，所采用的结构模型图如图2所示。模型由五类实体构成，具体阐述如下。

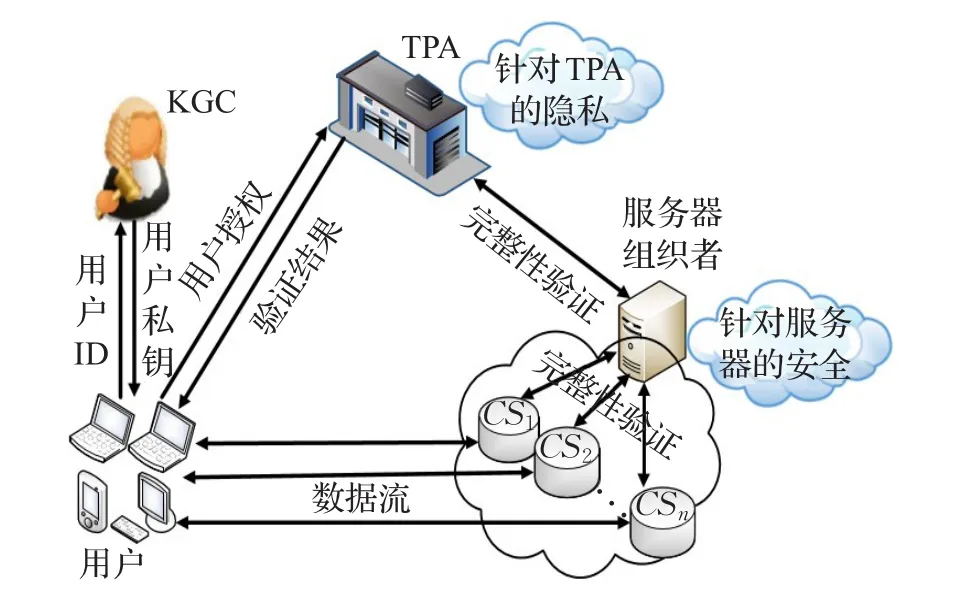
图2 IDB-RDIC结构模型图

用户：需要在不同的服务器上存储数据的多个用户，用户可以和云存储服务器通信来传输数据。

第三方审计（即校验者TPA）：获得用户授权的半可信代理，代替用户执行远程服务器上数据完整性验证的任务，并将验证结果返回给相应用户。

云存储服务器（CS）：由不同的云服务商CSP提供的服务器资源，具有强大的存储空间和计算能力，可以存储用户的数据信息并在收到挑战时计算拥有数据的证明。

服务器组织者（Organizer）：服务器CS和校验者TPA之间起连接作用的服务器，接受TPA的审计挑战并为被挑战的服务器分发挑战，聚合服务器返回的多个用户的数据块及标签证明，然后计算并返回最终回应给TPA。

秘钥生成器（KGC）：根据用户的身份计算用户私钥，然后通过一个安全的通道返回给相应用户。

2.2 安全模型

根据文献[11]中定义，方案IDB-RDIC的合理性和完美隐私性的模型定义如下。

定义1合理性（即针对服务器的安全性）。

（1）Setup：挑战者运行Setup算法，得到公开参数param和主私钥msk，将 param发送给敌手，私密保存msk。

（2）Queries：敌手对挑战者做一些提取Extract询问和标签TagGen询问。

①Extract Queries：敌手询问用户IDi的私钥。挑战者运行算法Extract得到私钥ski，将其发送给敌手。

②TagGen Queries：敌手对用户IDi询问文件Fi的数据标签，挑战者查询Extract并运行算法TagGen，生成文件Fi的标签集合，将其发送给敌手。

（3）ProofGen：敌手对文件Fi进行TagGen查询，并以用户身份IDi运行算法ProofGen。挑战者扮演TPA的角色，与敌手扮演的证明者角色进行交互，最后敌手得到挑战者的输出P。

则称敌手赢得了游戏。

定义2针对TPA的完美隐私性。

完美隐私是指TPA在和服务器交互过程时没有得到用户数据的任何信息。下面通过模拟器S来定义。假设存在一个多项式时间内的非交互模拟器S，对于公开输入IDi、chal、Tagi和非公开输入Fi，以下两个变量是计算上不可区分的：

则称方案针对欺骗性TPA∗具有完美隐私性。

3 IDB-RDIC方案

3.1 基础知识

（1）双线性映射：设G1、G2为阶为q（q是大素数）的乘法循环群，g为G1的生成元，则双线性映射e:G1×G1→G2满足：

①双线性：对于∀u,v∈G1和x,y∈Zq,有e(ux,vy)=e(u,v)xy；

②非退化性：e(g,g)≠1G2，其中1G2为群G2中的单位元；

③可计算性：对于∀u,v∈G1，存在有效的算法计算e(u,v)。

（2）离散对数的相等性：设G为阶为q（q是大素数）的乘法循环群，g1、g2均为G的生成元，如果P向V证明群元素Y1、Y2在生成元g1、g2上有相同的离散对数x，那么交互证明如下：

②V随机选择c∈{0 ,1}λ发送给P；

③P计算z=ρ-cx( )mod q，并返回z给V；

3.2 回顾ID-RDIC方案

ID-RDIC方案[11]在单用户单服务器环境下提出，方案的具体细节描述如下。

（1）Setup：输入安全参数k，KGC选取两个阶为q的乘法循环群G1、G2，构建一个双线性映射e:G1×G1→G2。KGC随机选取作为主私钥，主公钥设置为mpk=gα。KGC选择三个不同的哈希函数H1,H2:{0,1}*→G1和 H3:G2→{0,1}l。输出系统参数(G1,G2,e,g,mpk,H1,H2,H3,l,q)。

（2）Extract：输入主私钥α和用户身份ID∈{0,1}*,输出用户私钥。

（3）TagGen：用户将文件名为 fname的文件分成n个数据块，mi∈Zq,i=1,2,…,n；然后随机选取计算r=gη，并对每个数据块计算数据标签；最后将存放于服务器上。

（4）Challenge：校验者选取c个元素的子集合I⊆[1 ,n],并对 ∀i∈I,选取令挑战集合校验者随机选取计算，生成证明，将挑战发送给服务器。

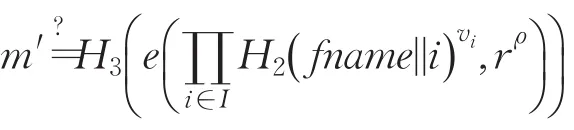
3.3 IDB-RDIC协议设计

本文构造了一个在多用户多服务器环境下支持批量校验用户数据的IDB-RDIC协议，协议由参数初始化(Setup)、密钥生成(Extract)、标签生成(TagGen)、挑战(Challenge)、证明(Prove)和批校验(BatchVerify)六个算法组成，并对挑战、证明和批校验算法进行了改进。其中，Challenge、Prove算法拆分为两个分算法执行，Challenge1、Challenge2及 Prove1、Prove2，BatchVerify算法用来实现对多个用户数据的批处理校验。图3为IDB-RDIC协议的数据传输图，算法详细步骤描述如下。

图3 IDB-RDIC数据传输图

（1）Setup(1k)→(params,msk)。算法输入安全参数k，KGC选取两个阶为q的乘法循环群G1、G2，构建双线性映射e:G1×G1→G2。令G1的生成元为g，KGC随机选取并设置主私钥msk=α,主公钥mpk=gα。KGC选择三个不同的哈希函数H1:{0,1}*→G1，H2:{0,1}*→G1和 H3:G2→{0,1}l。输出系统公开参数params=(l,q,G1,G2,e,H1,H2,H3,g,mpk),将msk私密保存。

（2）Extract(params,msk,IDi)→(ski)。算法输入主私钥msk和用户身份IDi∈{0,1}*及系统参数 params，输出用户私钥ski=H1(IDi)α，并安全地传送给相应用户。

DOi将文件块的索引集合表N={(i,j,k)}发送给服务器组织者Organizer，索引表包含用户索引i∈O，文件块索引和存放DOi第k个块的服务器索引。另外，DOi将值ri及其身份签名IDS(ri)也发送给Organizer。

（4）Challenge(params,{i,k},N)→(chal,chalj)。挑战阶段的算法分两步执行，具体如下：

①Challenge1(params,{i,k})→(chal)。校验者TPA随机选取c个元素的子集合I⊆[ ]1,n，并对每个k∈I，选取系数，令挑战集合为Q={( )}k,vk。TPA随机选取并计算c2=Zρ,生成知识证明TPA令总挑战为chal=(Q,c1,c2,pf),将chal发送给Organizer。

②Challenge2(chal,N)→(chalj)。Organizer验证知识证明的有效性，若有效，则根据存储的索引表N为被挑战服务器分发若干个分挑战chalj={ |(i,j,k),{vk}i∈Oj,j∈U,k∈Ij}。其中，U表示被挑战的服务器索引集合，Ij表示第 j个服务器上被挑战的数据块索引集合，Oj表示第 j个服务器上被挑战的云用户索引集合。

（5）Prove(p arams,{mijk},{σijk},{IDi},chalj) → (Pj,P )。证明阶段也由两部分算法构成：

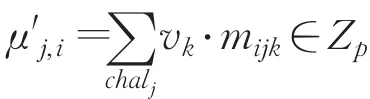
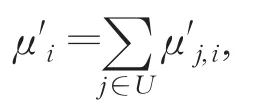
（6）BatchVerify( )params,{IDi},chal,P →1/0。TPA

4 IDB-RDIC安全分析

4.1 正确性证明

定理1如果服务器利用其上存储的数据块诚实地按照协议计算并返回相应的证明，那么该证明就可以通过TPA的校验，使等式（1）成立。

证明

证毕。

4.2 合理性证明

根据文献[11]，对方案IDB-RDIC的合理性证明如下。

定理2在一般性群模型和随机谕言机模型下，IDBRDIC方案是可证明安全的。

一般性群Gi表示为是两个独立的随机编码函数，p为素数。一般性算法是指没有利用群结构的算法，因此除了元素编码值以外，得不到其他任何信息。随机谕言机Oi,i∈{1 ,2}模拟群G1、G2的操作，输入元素，输出表示Oi上元素相乘的结果，输出表示相除的结果。另一个谕言机OE模拟双线性操作，输入G1中元素和，输出作为两个元素双线性运算的结果。

证明基于以上背景，下面证明本文方案在随机谕言机模型下针对一般性算法是可证明安全的。其中，敌手A扮演不可信云服务器的角色，且存在PPT模拟器S在与A进行||

I次交互后可提取出挑战的全部文件块值。

（1）Settings：S运行 Settings，得到公共参数 (l,q,，并将元素 g 的编码值 ξ1和一次的常量多项式对应，将元素mpk的编码值ξα与多元多项式α对应。

（2）Hash-Queries：A对用户IDi查询谕言机H1，S返回一个随机比特串ξIi，并与多项式Ii对应；A对文件块索引k查询谕言机H2,S返回一个随机比特串ξk，并与多项式k对应；A查询谕言机H3,S返回一个随机比特串值。

（3）Oracle-O1：A 将元素 ξF1、ξF2和两个整数 e1、e2发送给S，询问随机谕言机O1的结果，S查找是否有与元素ξF1和ξF2对应的多项式F1和F2存在。

①若不存在，S拒绝执行。

②若存在，S计算多项式F3=e1F1+e2F2并查找历史是否存在元素ξ∈G1，其对应的多项式为F3。若存在返回ξF3给A；若不存在，S随机选择一个比特串ξF3与多项式F3对应，然后将ξF3返回给A。

（4）Oracle-O2：与随机谕言机O1的操作相同。

（5）Oracle-OE：A将元素 ξF1、ξF2发送给S，询问随机谕言机OE的结果，S查找是否有与元素ξF1和ξF2对应的多项式F1和F2存在。

①若不存在，S拒绝执行。

②若存在，S计算多项式F3=F1⋅F2并查找历史是否存在元素ξ∈G2，其对应的多项式为F3。若存在返回ξF3给A，否则，S随机选择一个比特串ξF3与多项式F3对应并将ξF3返回给A。

（6）Extract Query：A将IDi发送给S，询问该用户私钥。S首先进行H1查询，得到与多项式Ii对应的元素ξIi，然后查找历史是否存在元素ξαIi，其对应的多项式为αIi。若存在，S发送ξαIi给A，否则，S随机选择一个比特串ξαIi与多项式αIi对应，并将ξαIi返回给 A。

（7）TagGen Query：A将身份IDi和文件块集合Mi=发送给S，询问文件块的数据标签。S对IDi进行Extract查询，得到与多项式αIi对应的元素ξαIi，并对文件块索引k进行H2查询，得到与多项式k对应的元素ξk，然后S随机选取比特串ξηi与多项式ηi对应并计算Fi,k=αIimik+kηi。S查找是否存在与元素ξFi,k对应的多项式Fi,k，若存在，S发送ξFi,k给A，作为文件块mik的标签，否则，S随机选择一个比特串ξFi,k与多项式Fi,k对应，并将ξFi,k返回给A。另外，S把元素ξηi和用户IDi的身份签名IDS()ri也返回给A。

（8）Challenge：A对用户IDi*及其文件块集合Mi*=发起挑战，要求敌手A之前未对IDi*进行过Extract查询。S随机选取挑战集合并对所有k∈I随机选取vk。S随机选取比特串ξc1与多项式ρ对应，选取随机比特串ξZ与多项式αIi*对应，选取随机比特串 ξc2与多项式 αIi*ρ 对应，将 ξc1、ξc2及知识证明 pf发送给A。

（9）GenProof：A返回值m′，群元素ri*和对其签名IDS(ri*)作为回应证明。

返回证明m′之前，A需要进行一些群操作的询问，在挑战阶段之前A会对群G1中元素进行询问，询问元素对应的多项式形式为：

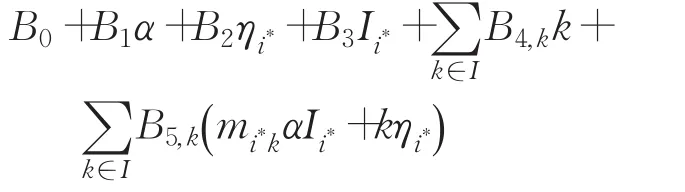
敌手A知道上式中所有系数。

A对已知的群G1中元素和元素值ρ查询随机谕言机OE并返回证明m′，其对应的多项式形式为：

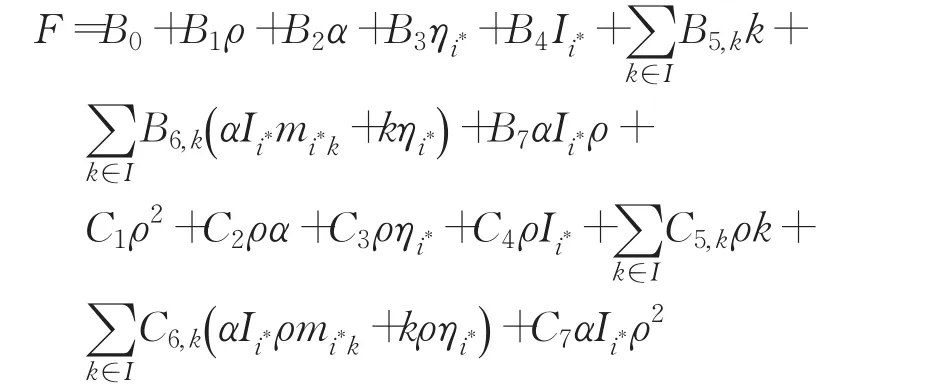
此时，A和S已知多项式F中所有系数。将多项式F与等式（1）右边元素对应的多项式联立，即：

4.3 完美隐私性证明

根据文献[11]，对方案IDB-RDIC的隐私性证明如下。

定理3 IDB-RDIC方案针对校验者TPA具有完美隐私保护性。

证明构造一个模拟器S回应校验者V的挑战。首先，因为ri和 IDS()ri不包含文件块的任何信息，所以可将{ri,IDS(ri)| i∈O} 发送给模拟器S。其次，S在收到V发送的挑战chal=(c1,c2,Q,pf )后，解析 pf:并从中提取值ρ。根据值ρ计算回应最后输出回应(m ′,ri,IDS(ri))i∈O给V。输出的回应与V和真实服务器交互得到的输出具有不可区分性，因此方案针对TPA实现了完美隐私。证毕。

5 IDB-RDIC性能及实验分析

5.1 性能分析

本文提出多用户多云存储环境下支持批处理校验的IDB-RDIC方案，并与文献[11]在多用户多服务器环境下可拓展的方案（简称为ID-RDIC方案）进行了性能对比分析，ID-RDIC的结构模型图如图1所示。本文分别从存储复杂度、计算复杂度和通信复杂度上进行对比，并假设m个用户被挑战，每个用户的文件块总数为n，每个用户被挑战的文件块数量为c。

（1）存储复杂度的比较

用户将自己的文件块及数据标签存储在云服务器CSj上，存储形式为：

本文方案IDB-RDIC增加了服务器Orgniser来执行分发挑战和聚合证明的任务，因此增加的存储内容为索引集合表N=(i ,j,k)和用户的身份签名ri||IDS(ri)，存储形式为：

考虑到椭圆曲线上的签名一般包含两个点，因此本文方案增加的存储复杂度为

（2）通信复杂度的比较

本文从挑战和证明两个阶段对比了本文方案IDBRDIC和ID-RDIC方案[11]的通信复杂度，如表1所示。现将对比结果分析如下：

挑战阶段，IDB-RDIC由两部分构成。在Challenge1中，TPA发送总挑战chal=( )c1,c2,Q,pf 给Organizer,其中c1、c2是两个群Zq中元素包含c个整数和c个Zq中元素，pf中包括2个Zq中元素，主要考虑群上元素的通信开销，Challenge1阶段的通信开销用比特串的长度表示为；在Challenge2中，Organizer将分挑战发送给CSj，包含c个群Zq中的元素，其通信开销为综上，IDB-RDIC方案挑战阶段的通讯复杂度为O(c)。在ID-RDIC方案中，需要分别为m个用户分发挑战，因此ID-RDIC挑战阶段的通信开销为，总体的通信复杂度为

证明阶段，IDB-RDIC也由两部分构成。在Prove1中，CSj向Organizer返回有关m个挑战用户的证明，其中 μ′j,i、σ′j,i为 Zq中元素，故Prove1的通信开销用比特串长度表示为在 Prove2中，Organizer向TPA返回证明 P={m′,{ri,，其中m′的比特串长度为l，签名的长度为320 bit，ri的比特串长度用表示，Pr ove2的通信开销为。综上，IDB-RDIC证明阶段的通讯复杂度为O(2 m )。在ID-RDIC方案中，服务器分别返回m个被挑战用户的证明所需的通信开销为，故其通信复杂度为O(m)。

表1 通信复杂度的比较

表2 计算复杂度的比较

综上所述，本文方案在证明阶段的通信复杂度略有增加，但在挑战阶段复杂度明显降低，因此IDB-RDIC拥有更低的通信复杂度。

（3）计算复杂度的比较

令P表示单个双线性对运算的开销，H表示单个哈希函数运算的开销，EG1、EG2分别表示群G1、G2上单个指数运算的开销，MG1、MG2分别表示群G1、G2上单个乘法运算的开销，MZp表示整数群Zp上单个乘法运算的开销，AZp表示整数群Zp上单个加法运算的开销，对比分析本文方案IDB-RDIC与ID-RDIC方案[11]的计算复杂度，如表2所示。

从表2中可看出，本文方案在用户端的计算复杂度上没有变，这是因为用户端的计算复杂度和文件块的数量成正比。但在TPA验证端和云服务器端上比ID-RDIC[11]方案拥有更低的计算复杂度。这是因为IDB-RDIC方案支持批处理校验，使得TPA验证端减少了两大主要计算开销，包括(m-1)次P运算及c(m-1)次EG1运算。服务器端也减少了(m-1)次P运算、EG1运算、EG2运算这些主要运算开销。

5.2 模拟实验

模拟实验使用的软硬件配置如下：

PC硬件配置：Ubuntu 16.04 LTS 32位操作系统，4 GB内存，Intel Core2Duo处理器。

软件配置：Miracl库、PBC库、GMP库。

实验设置10个用户的文件分散存储在10个服务器上，每个用户文件大小为2 MB，总挑战块数3 000～4 600（相应的每个服务器上挑战300～460），步长200，模拟对比IDB-RDIC方案和ID-RDIC方案[11]在云服务器端的计算复杂度，如图4所示。图5设置总挑战块数1 000～5 000，步长500，模拟TPA验证端的计算复杂度对比。

从图4和图5可得，IDB-RDIC方案显著降低了TPA端的计算复杂度，也降低了服务器端计算复杂度，实验结果与性能分析结果一致。特别地，当云服务器损毁数据块率为1%时，TPA挑战其上460个数据块，就能以99%的概率检测出服务器的损毁数据行为[15]。因此当总挑战块数为4 600时，IDB-RDIC方案的服务器计算证明时间开销为11.7 s，检测出10个服务器损毁数据行为的时间开销为1.18 s。