任意空间位置下改进的互感系数计算方法

熊慧 刘来 刘近贞

1. 天津工业大学 电气工程与自动化学院，天津 300387；2. 天津市电工电能新技术重点实验室，天津 300387

一、引言

近年来，无线能量传输技术在电动汽车、手持电子设备、工业制造以及植入式医疗设备等领域的应用给人们的生产和生活带来了巨大的便利，磁耦合谐振式无线能量传输技术在传输效率、有效传输距离以及安全性等方面有着独特的优势，所以在植入式医疗设备领域有着很广泛的应用前景[1-2]。

在无线能量传输系统的设计过程中，传输效率是衡量系统传输性能的指标之一，而互感系数是影响传输效率的关键性参数之一。由于植入式医疗设备的尺寸限制，接收线圈的尺寸也受到制约。在实际使用中，两个线圈之间的相对空间位置的变化也是不可避免的，比如说轴心偏移、横向偏移以及角度偏移。综上所述，线圈的尺寸以及线圈之间的相对空间位置的变化对互感系数的影响是设计人员在对系统优化过程中所必须考虑的。

对于两个空心线圈之间的互感系数的计算，已经有许多文献进行了研究。这些文献是基于椭圆积分[3-4]、近似公式[5]、贝塞尔函数[6]、聂以曼公式[7]以及毕奥-萨伐尔定律等方法[8]。

在线圈的空间位置方面：文献[3,6,8]研究的是同轴空心线圈之间的互感系数，文献[5,7]计算了不同空间位置下线圈之间的互感系数；在线圈类型方面：文献[4,7-8]研究的是螺线管线圈，文献[3,5,6]研究的是单层平面螺旋线圈。除此之外，一些学者提出了多层平面螺旋线圈结构，这种线圈结构可以在一定尺寸限制下通过提高线圈的互感系数和品质因数来提高传输效率[9-11]。虽然在无线能量传输技术的应用中，对互感系数研究的成果有很多，但是关于多层平面螺旋线圈之间互感系数的研究成果很少，因此对多层平面螺旋线圈之间互感系数需要进一步的研究。

本文根据聂以曼公式提出了一种改进的互感系数计算方法，将多层平面螺旋线圈的层数和匝数参数化，并使用ANSYS有限元仿真软件和测量实验验证了本计算方法的正确性，设计了精确测量两个线圈在轴心偏移、横向偏移和角度偏移情况下的互感系数的装置。本文所提出的理论模型不仅可以计算出两个不同相对空间位置下空心多层平面螺旋圆线圈之间的互感系数，而且同样可以适用于螺线管线圈和平面螺旋圆线圈。此外，该理论模型对无线能量传输系统中线圈参数的设计和优化具有参考意义。

二、互感系数的理论计算

1、单匝线圈之间的互感系数

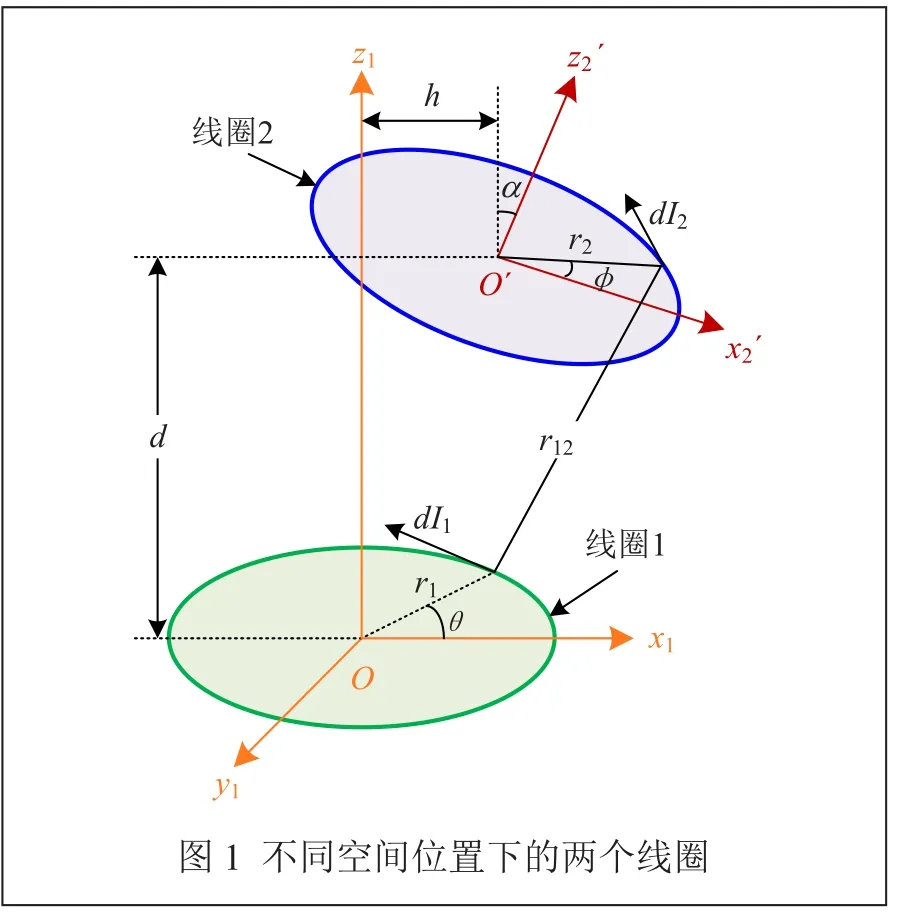
图1所示为处于不同空间位置下的两个单匝圆形细导线。假设线圈1位置不变，仅改变线圈2相对于线圈1的相对空间位置，则根据聂以曼公式，两个线圈之间的互感系数MS为：

其中，μ0—真空磁导率；

dI1、dI2—两个载流线圈的微元；

r12—两个微元之间的几何距离。

为了简化分析，本文将两个线圈之间的相对位置分解为三种单一的情况：轴心偏移、横向偏移和角度偏移。图1为不同位置下的两个线圈，其中d为轴心偏移距离，h为横向偏移距离，α为偏转角度，r1、r2分别为线圈1与线圈2的半径。则在笛卡尔坐标系下，微元dI1所在点在全局坐标系下的参数方程为：

相对于全局坐标系，微元dI2所在点在局部坐系下的参数方程为：

经过坐标变换之后得到微元dI2所在点在全局坐标系下的参数方程为：

根据空间中两点距离公式可以计算得出r12：

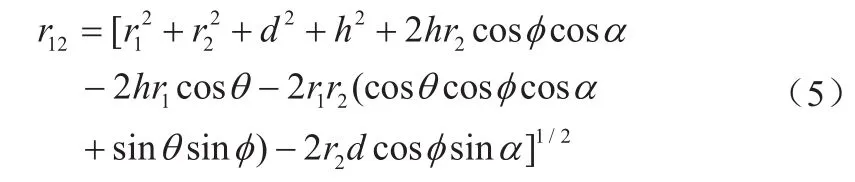
由公式（1）和（5）可以得到任意空间位置下单匝圆线圈之间的互感系数的计算公式[7]：

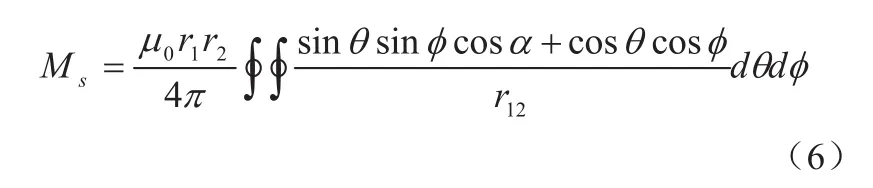
2、多匝线圈之间的互感系数

目前在无线能量传输系统中，大部分人使用的多匝线圈可分为两大类：第一大类是螺线管线圈，第二大类是平面螺旋线圈。

文献[7]使用聂以曼公式对不同空间位置下的螺线管线圈之间的互感系数ML进行计算，并验证了计算结果的准确性，其计算方法为：

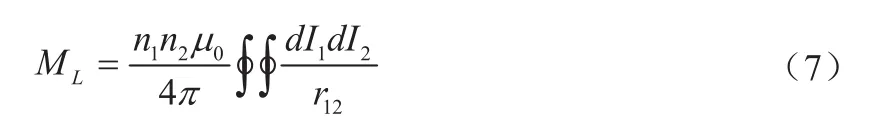
其中，n1、n2—线圈1、2的匝数。

文献[5]使用聂以曼公式的简化公式对单层平面螺旋圆线圈之间的互感系数MP进行计算，并验证了计算结果的准确性，其计算方法为：

其中，Mij—线圈1中第i匝和线圈2中第j匝之间的互感系数。

针对多层平面螺旋线圈之间的互感系数MD的计算，基于公式（7）和（8）的计算思想，本文从叠加原理的角度出发，提出一种改进的互感系数的计算模型。这种方法将多层平面螺旋圆线圈在径向上看作多匝平面螺旋圆线圈，在轴向上看作多匝螺线管线圈，所提出的计算模型为：

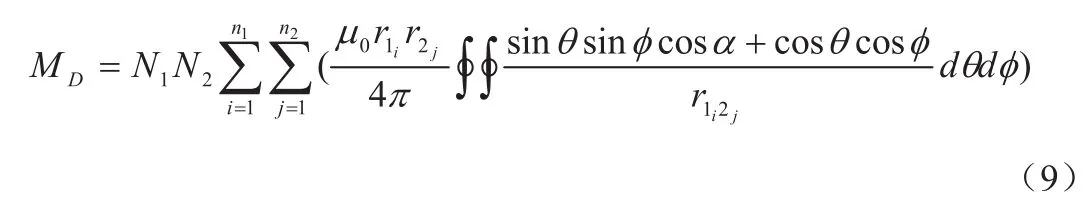
其中，N1、N2—线圈1和线圈2的层数；

n1、n2—线圈1和线圈2每层的匝数。

三、仿真和实验

1、有限元仿真

为了验证所提出计算方法的正确性，本文使用ANSYS有限元仿真软件对两个空心圆线圈之间的互感系数进行仿真求解，并设计了互感系数实验测量平台，实验中所选线圈参数与仿真实验保持一致。所设计线圈层数为2层，每层10匝，线圈的内半径为10.22mm，铜导线的直径为1.10mm。

ANSYS中的Plane53单元和Solid97单元均可对两个线圈之间的互感系数进行仿真求解，其中Plane53单元可用于二维轴对称磁场问题建模，仿真速度快、精确度高。Solid97单元适用于三维磁场问题，其功能与Plane53单元相似，更适用于两个线圈出现相对空间位置变化的建模仿真。根据Plane53单元以及Solid97单元各自的优点建立线圈仿真模型。图2为使用Solid97单元求解两个线圈出现横向偏移或角度偏移时，互感系数的变化情况下建立的仿真模型。

2、实验验证

图3为互感系数测量电路原理图，图中一次侧包含一个高频交流激励源和一个LC谐振电路，二次侧线圈开路。互感系数ME实验测量计算公式为[12]：

其中，V1、V2—线圈L1和线圈L2两端的电压。

为了简化分析，本文仅考虑了线圈间相对空间位置的变化对互感系数的影响，并未考虑工作频率等参数对互感系数的影响。

为了更精确的测量两个线圈发生相对空间位置变化时的互感系数，本文设计了一组互感系数

测量平台，并使用3D打印机将三个测量装置打印出来，所使用的打印材料为PLA塑料，对磁场不会产生影响。该平台对线圈空间位置变化下互感系数的测量均在一次侧线圈固定的前提下进行的，实验平台如图4所示。

四、结果

根据所提出互感系数计算方法，利用MATLAB软件，对轴心偏移、横向偏移和角度偏移三种情况下的互感系数进行理论计算并与仿真值和实验测量值进行对比验证，并分别计算出每组仿真值和实验值与理论值之间的相对误差。

1、轴心偏移

固定h=0mm、α=0°不变，仅使轴心偏移距离d在0mm～80mm范围内变化，使用Plane53单元对双层平面螺旋圆线圈建立仿真模型并进行互感系数的轴心偏离仿真，使用图4（b）测量装置进行实验测量。将得到的仿真数据和实验数据分别与理论计算数据进行分析对比，结果如图5所示。

从图5（a）和（b）两图的左纵坐标轴均可以看出，随着d的增加，互感系数逐渐减小。从右纵坐标轴可以看出，理论计算值与仿真值之间的相对误差低于1%，理论计算值与实验值之间的相对误差低于2%。

2、横向偏移

固定d=20mm、α=0°不变，仅使横向偏移距离h在0mm～20mm范围内变化，使用solid97单元对双层平面螺旋圆线圈建立仿真模型并进行仿真，使用图4（c）测量装置进行实验测量。将得到的仿真数据和实验数据分别与理论计算数据进行分析对比，结果如图6所示。

从图6（a）和（b）两图的左纵坐标轴均可看出，随着横向偏移距离的增加，互感系数逐渐减小。从右纵坐标轴可以看出，理论计算值与仿真值之间的相对误差低于1%，理论计算值与实验值之间的相对误差低于2%。

3、角度偏移

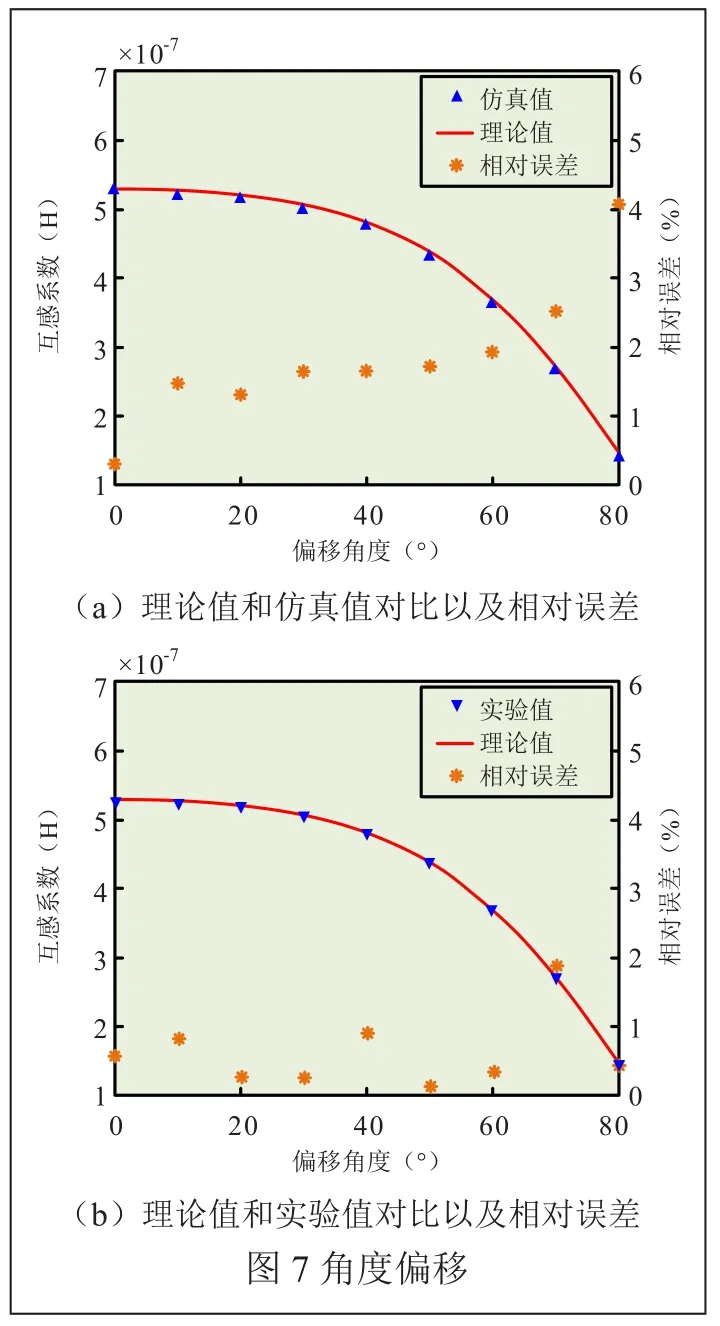
固定d=40mm、h=0mm不变，仅使偏移角度α在0°～80°的范围内变化。使用Solid97单元对双层平面螺旋圆线圈建立仿真模型并进行仿真，使用图4（d）测量装置进行实验测量。将得到的仿真数据和实验数据分别与理论计算数据进行分析对比，结果如图7所示。

从图7（a）和（b）两图的左纵坐标轴均可看出，随着偏移角度的增加，互感系数逐渐减小。从右纵坐标轴可以看出，理论计算值与仿真值之间的相对误差低于4%，理论计算值与实验值之间的相对误差低于2%。

在Ansys软件的仿真中，不同的网格剖分会带来离散误差，这是相对误差的主要来源。另外，本文通过多次测量求平均值的方法来减小实验过程中存在的随机误差。从图5 ～图 7中可以看出相对误差均低于5%，在工程允许误差范围之内。以上结果表明，本文所提出的计算方法，可以准确的计算出多层平面螺旋线圈之间的互感系数。

五、结论

本文分析了磁耦合谐振式无线能量传输系统，并得出影响传输特性的关键性参数。针对多层平面螺旋圆线圈提出了一种改进的互感系数计算方法，并且通过有限元仿真和实验测量验证了所提出计算方法的正确性。最后，这种计算方法还适用于不同空间位置下的螺线管线圈之间或者单层平面螺旋圆线圈之间的互感系数计算，为无线能量传输系统设计过程中线圈参数的优化提供了理论依据，具有一定的参考意义。