基于改进粒子群算法的风电并网的无功优化研究

易继泽，傅晓锦，陈建全

（上海电机学院，上海 200120）

0 引言

风能作为可持续、绿色的新能源被大幅度用于风力发电，但由于风的不确定性、不稳定性，使得风电系统的输出功率具有波动性[1]，因此当风电接入电网时，风电并网系统会对电网系统产生较大幅度的电压波动和闪变，同时，风电场装置中的电子器件也易发生谐振现象，容易发生风电的运行事故[2]。因此接入的风电会影响整个电力系统的电能质量以及安全稳定的运行，若不采取相应措施来解决这些问题，将会造成巨大经济损失，尤其是解决风电并网对电网稳定性影响的问题。目前，风电场并网的研究主要集中在风电场的低压穿越能力、风功率预测和风电场的无功装置安装的位置以及无功功率补偿上[3]。本文首先对风电并网带来负面影响、系统无功优化的数学模型、粒子群算法等各个方面进行了阐述与研究，其次指出了存在的问题和改进方法以及基于改善后粒子群算法的风电并网系统无功优化方案，最后通过MATLAB在IEEE 9节点风电系统中仿真验证了改进算法的有效性及实用性。

1 风电并网系统对于区域电网的主要影响

风电并网过程会对电网产生冲击，风机在连网之前处于空转状态，在启动、断开瞬间将会产生巨大的冲击电流（该值为电力系统额定电流的5～6倍）。当风力发电机系统与电网相连时，电网具备的感应负载特性使得电网络相当于一个巨大的电抗器，导致瞬时变化的电流将形成巨大的冲击电流，进而冲击区域电网，降低区域电网的稳定性，同时会导致网络损耗，从而使得电网运行效率变低[4-6]。

由于风速的不确定性的变化，风力发电机可能会导致无功功率的吸收。而且，由于风机的尾流效应、湍流和风速变化迅速将会引起的湍流会引起风功率的波动和风力机的频繁启停，最终这将影响系统正常运行[7-8]。风电的不稳定性势必引起电网电压变化，其主要表现为周期性的电压波动、电压骤降、电压闪变及电气设备损坏等[9]。

风电并网会影响区域电网的运行成本，由于风能不能有效控制，会严重破坏电网的有功功率平衡。为了保证风电并网后供电的可靠性，需要增加热备功率，以避免因输出变化而引起的有功功率短缺，从而实现电力系统的有功功率平衡。这是因为有功不足不仅会影响系统的有功功率平衡，而且基于工频静态特性对系统无功功率损耗有影响，改变无功电压平衡[10-13]。

2 无功优化的作用与数学模型

2.1 无功优化的作用

基于无功优化，对电网运行进行改进[14-15]：① 降低电网崩溃甚至停电的事故率，提高电网的电能质量以及运行安全性；② 将电网相关点的电压控制在标准范围内，确保电网发电机所发电量能够满足供电需求；③ 合理分配和减少电网的无功损耗，减少无功功率设备的使用，减少变压器、线路的负荷；④ 通过节能装置减少电能的损耗继而降低有功损耗，实现电网更加经济性运行；⑤ 通过合理安排无功补偿容量和位置，减少无功装置与无功电源的建设投资。因此，合理稳定电力系统的电压、优化系统无功功率以及提高电网电能质量是维持系统安全稳定运行的重要前提。

2.2 无功优化数学模型

无功优化问题是电力系统中较为复杂的非线性、多变量、多约束的一个规划问题,变量通常是离散变量和连续变量，这两种变量既有相互联系又有制约，约束条件中包括等式和不等式约束[16]。必须要保证无功补偿装置输入容量、变压器分接头的调节以及发电机端电压的协调合适等条件。而且收敛依赖于初始值以及变量的数量，这是一个非常复杂的问题。

无功优化常用的数学模型包括目标函数和约束条件两部分[17]。优化模型的通常数学模型为：

式中，u为控制变量；x为状态变量；f(u，x)为电力系统无功优化目标函数；g(u，x)为等式潮流约束条件；h(u，x)为不等式变量约束条件。

若在系统状态变量超出可行范围时，需对目标函数增添罚值：

式中，λ1、λ2为罚值常数，Mi为系统状态变量，Milim为状态变量限制值。

最后的目标函数为原始目标函数与罚值之和：

式中，F1为原始目标函数，ΔF 为罚值函数。

3 基本粒子群算法

3.1 算法理论

算法的基本原理是[18]：随机生成一定规模大小的初始粒子群。这些粒子在解空间中移动，且具有它们自己的当前位置和瞬时速度，粒子的维数等于控制变量的数目。粒子的位置是优化问题的可能解，并且速度对应于迭代期间产生的偏差量。将已知粒子位置值代入到适应值求解方程，得到当前位置处的粒子函数值，并用于评估粒子的质量。通过对所有最佳位置点的分析和比较，选择最佳的位置点。但是一般粒子将围绕该最佳点移动并通过连续迭代搜索获得全局最优解。在每次迭代中，每个粒子由遵循两个最优解的规则来确定其速度和位置：一个是单个粒子经历的最优位置，即单个最优解；另一个是当前的最优位置由粒子群总体找到的，则这个最优位置为全局最优解[19]。

若已知某粒子群个体总数为N，且每个粒子的搜索的空间维度为D维[20]，则：第i个粒子在该空间中，位置矢量为：xi=A（xi1,xi2,…xid,…,xiD）；速度矢量表示为：vi=（vi1,vi2,…vid,…,viD）；粒子当前的所有经历最优位置Pbest表示为：Pi=（Pi1,Pi2,…Pid,…,PiD；群体的全局最优位置解gbest为：Pg=（Pg1,Pg2,…Pgd,…,PgD）；在每次的循环中，每个粒子要调整自己的速度和位置将要用式（4）代入求解：

其中，ω为惯性权重，k为循环总数，c1、c2为学习因子，r1、r2为[0,1]范围内的随机值。

PSO算法对速度的约束条件[20]：

其中，vmax是粒子移动快慢的上限，vmin是粒子移动快慢的下限，为提高粒子的搜索精度，避免搜索到局部最优而无法跳出，必须合理选择vmax值。

3.2 粒子群算法改进的方案

上文所介绍的粒子群算法为未改进的算法，在标准粒子群算法中，根据粒子的收敛特性，粒子的收敛是以飞行轨迹的形式实现的。由于粒子速度的限制而使搜索的范围不能扩展到整个可行解空间，也因此导致了搜索空间的每个迭代步骤的有限区域。PSO算法由于其收敛性较为发散，因此最大的缺点弊端是不能保证完全搜索到全局最优解。可以通过改善PSO的收敛性来改进PSO算法，本文中采取非线性惯性权重的方法，则更新惯性权重ω和粒子速度v公式为

式中：ωa，ωb分别为惯性权重初始值与最后值，Mamax为粒子进行迭代时的最大迭代次数；pti为第t次迭代的个体极值；ptg为第t次迭代的群体极值，a1和a2为两个加速常数。

3.3 改进后PSO算法的原理流程图

改善后PSO算法原理流程图如图1所示：

图1 改善后PSO算法原理流程Fig.1 Improving the principle flow of PSO algorithm

4 改进后的粒子群算法在风电并网系统的无功优化中的应用

随着接入电网的风电容量逐渐增加，风电系统会导致电网电能质量下降，在严重的情况下，甚至会导致电网系统崩溃和停电。因此，本文采用改进后的粒子群算法，通过对变压器分接头的位置、风机端电压的大小和无功补偿容量以及无功装置的位置作为控制变量进行优化设置，达到稳定风电并网系统中的电压以及补偿系统无功功率来改善电网的电能质量和安全稳定运行。

以风电并网系统的网络损耗最小作为目标函数，则其表达式为

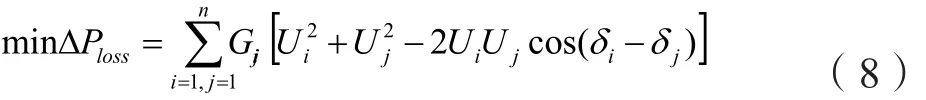
式中：i、j为节点编号；n为并网系统的节点总数；Gij为支路电导；Ui、Ui为节点i、j电压的幅值；δi、δj为节点i、j电压的相角。

以系统的潮流方程为等式约束条件：

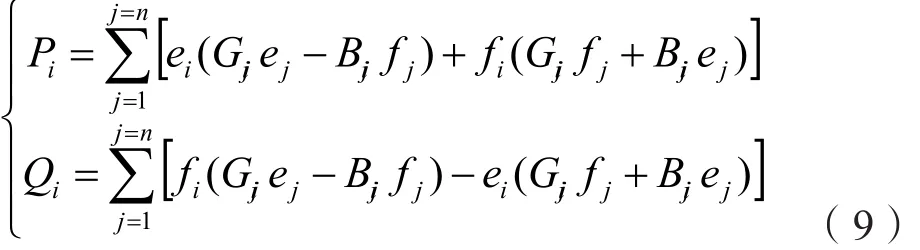
对于 PV 节点，还需增加约束方程：

最终优化结果的可行范围还需满足电压和无功安全性约束等条件：

在系统电压超出可行范围时，则有式 有：

最后风电并网系统的目标函数为有功功率损耗与罚值之和：

5 算例分析

为了验证改进粒子群算法的有效性和实用性，在MATLAB中对IEEE 9风电系统进行了仿真，并对改进算法前后进行无功优化后的有功损耗和节点电压进行了分析和比较。IEEE 9节点系统的拓扑结构如图2所示。有三个电源，九个节点和九个分支，三个分别连接到节点1, 2和3，将风力发电机分别接于节点 4、7、9，相关参数如表 1：

表1 不同数量的风机并网参数Table 1 Fan connected parameters

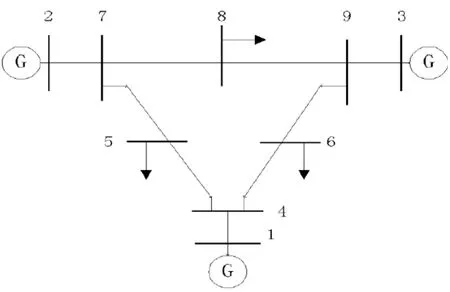
图2 IEEE 9节点风电系统拓扑图Fig.2 IEEE 9 node system topology

5.1 仿真结果

将原有粒子群算法应用于风电系统无功优化后的结果作为对照组与改进后的粒子群算法的仿真结果进行了比较。图3和4是改进前后粒子群优化算法的迭代收敛曲线。在表2中记录改善PSO前后优化后的结果。

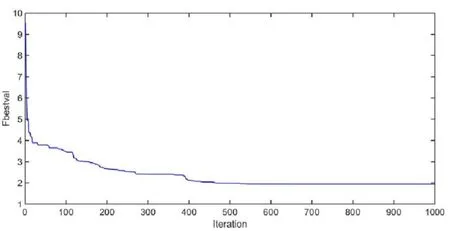
图3 改善前粒子群算法的迭代收敛曲线Fig.3 Improving iterative convergence curve of PSO algorithm

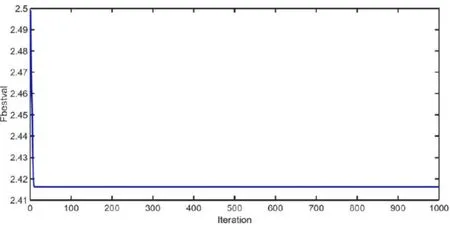
图4 改善后PSO优化算法迭代收敛曲线Fig.4 Iterative convergence curve of improved PSO optimization algorithm

在PSO改进前后优化后，分别记录有功损耗和主要控制变量，包括各发电机的无功输出、各发电机端的电压以及并联电容器的安装容量。相关数值如表2所示。

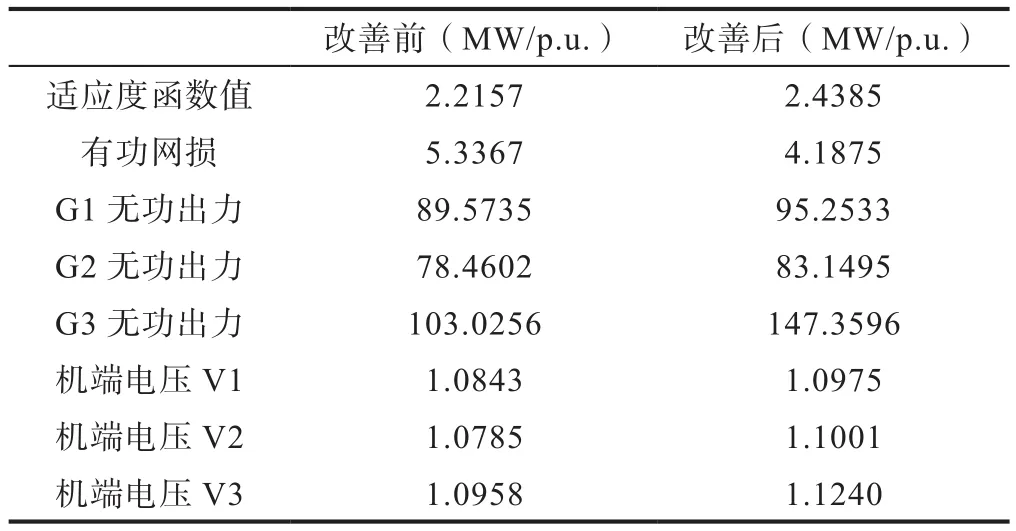
表2 改善PSO前后进行无功优化的结果对比Table 2 Simulation results of PSO optimization after node system improvement

针对PSO优化前的控制变量参数而言，改善PSO后无功优化系统中的因变量节点的电压也得到了优化。比较风电连入电网前后的节点电压以及改进前后PSO算法优化后的节点电压，绘制了上述对比的节点间电压表3和电压对比曲线图5，并进行对比分析。

根据以上数据，绘制成曲线图如图5所示。

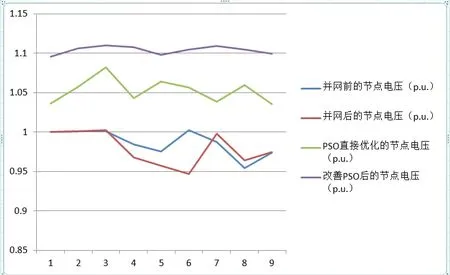
图5 改进前后PSO算法所得系统节点电压曲线图Fig.5 The PSO algorithm is used to optimize the voltage curve of the node before and after improvement

5.2 数据处理

由公式有：

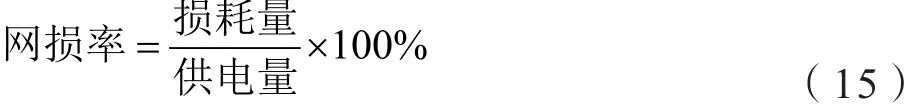
则在IEEE9节点风电并网系统中，根据潮流分析计算出接入风能后用改进PSO前后进行优化电力系统发电机的有功出力，最终算得各数据对比变化如表4：

表4 PSO进行优化前后各数据对比Table 4 Comparison of data before and after PSO optimization

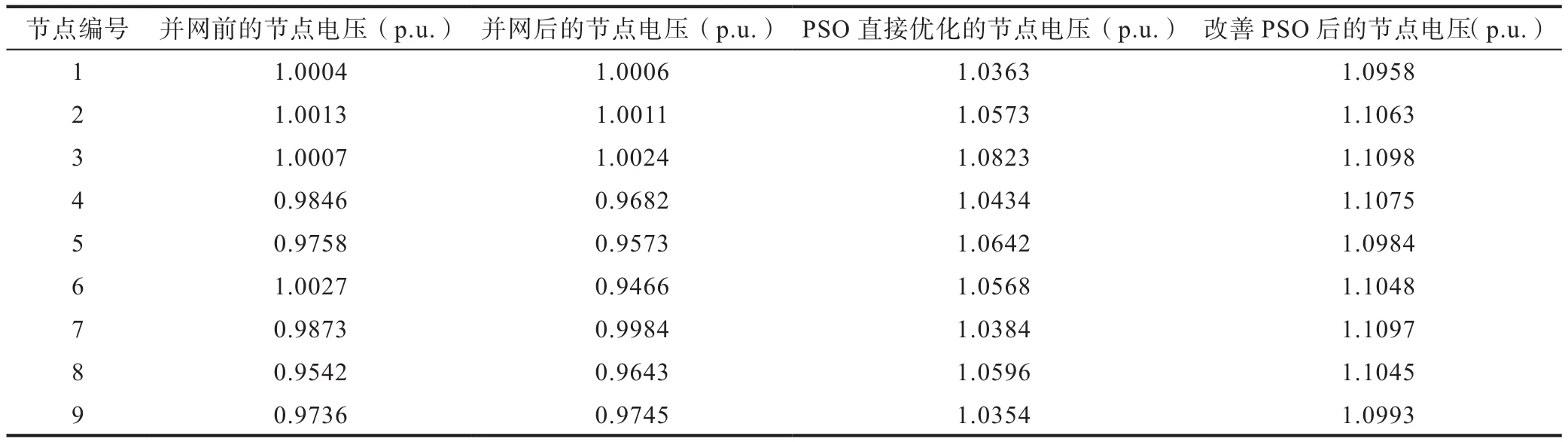
表3 9个电压节点风电系统的节点电压表Table 3 Node voltage meter of IEEE9 node system

5.3 结果分析

通过对比改善前后PSO进行无功优化后的网损值，可以得出这样的结论：经过改善PSO算法后再优化，风电并网系统的总有功损耗从5.2776MW下降至4.3658MW，下降了17.8474%，同时，网损率由改善PSO前的1.7278%下降了至1.3178%，降低了14.3046%。此外，图4中列图的趋势表明，系统节点电压比改进PSO之前的节点电压更稳定，并且改进算法后节点电压电平有效地增加，并且电压分布显著改善。以上结果还表明，本文提出的改进算法可以进一步降低系统损耗，而且能更有效地减小电压偏移，达到更好的优化效果。

6 结论

本文建立了风电并网系统的无功优化数学模型，并利用改进的粒子群优化算法对IEEE 9节点系统进行仿真和优化。结果表明改进算法具有较好的收敛性，通过比较改进前后算法的优化数据，发现优化后的网络损耗进一步降低，电压分布显著改善，从而改善了电力系统的电能质量以及达到电网稳定运行的条件，验证了改进的粒子群优化算法的有效性和实用性。