三角公式

◎任毓华

三角是中学生们学习数学的最基本内容之一，是继小学算术、初中代数之后的一块最基础内容；只要想一想在初中数学中，代数（学）内容和所占据位置，就不难领会作为高中数学内容的三角（学）了；而且，三角还作为一种工具（方法）直接或者间接地参与解决数学问题，譬如：复数中有其三角式、解析中直线和圆锥曲线的参数方程、求解三角形时候运用到正弦定理余弦定理、乃至物理上的振动、波……。三角公式是组成三角的主要内容之一、常被称作“三角恒等变换”、与三角函数联系紧密，掌握三角公式为提高数学推理能力和运算能力提供了广阔的空间和领域！

掌握三角公式，首先需要记住这些公式。下面分类汇总，有的配以“口诀”要领。

第一类：诱导公式

sin cos tan cot公式一 α±2kπ sinα cosα tanα cot处理的角α公式二 α±π -sinα -cosα tanα cot α公式三 -α -sinα cosα -tanα -cot α公式四 π-α sinα -cosα -tαnα -cot α公式五 π2+α cosα -sinα -cotα -tan α公式五 π α公式六 3π2-α cosα sinα cotα tan α公式六 3π2-α -cosα -sinα cotα tan α 2+α -cosα sinα -cotα -tan

第二类：同角三角函数的基本关系式

1、倒数关系

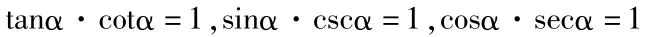
2、商的关系

3、平方关系

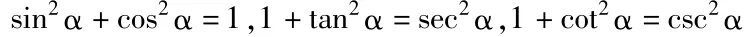
同角三角函数关系六角形记忆法：

构造以“上弦、中切、下割；左正、右余、中间1”的正六边形为模型。

倒数关系——对角线上两个函数互为倒数；

商数关系——六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。

平方关系——三个倒三角形中，上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。

第三类：包含两个角的三角函数式的公式（变换）

1、两角和与差的正弦、余弦和正切公式

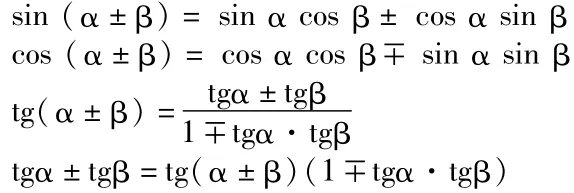
2．1二倍角的正弦、余弦、正切公式

2．2三倍角公式

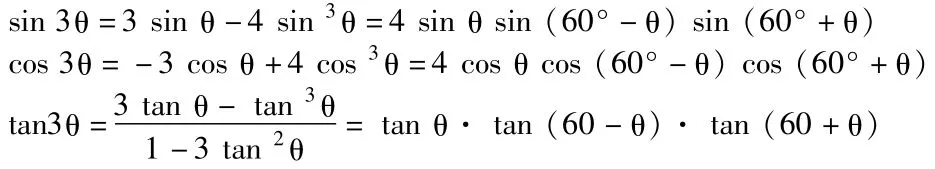
2．3万能公式；

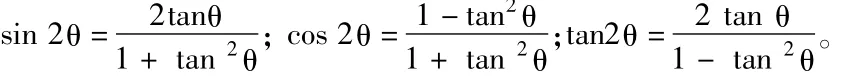
3、半角公式

有的地方又叫做降次公式。

4．1积化和差公式

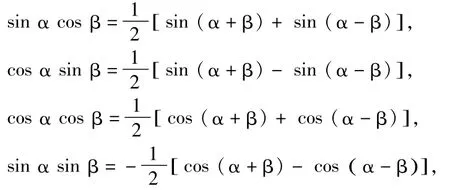
4．2和差化积公式

第四类：转化为形式Asin（ωx+φ）蕴含了化归思想的三角公式。

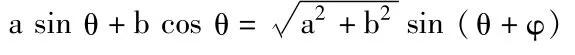
要熟练掌握三角公式，关键在于正确应用到解决问题之中。

分析：应用诱导公式，化简得-cosα．

分析：先用同角三角函数的公式得出cosα、cosβ，再用两角差的余弦公式求出coa（α-β），从而确定α-β的值。

解∵α、β均为钝角，∴cosα、cosβ均为负值，结合已知得 cosα＝-，由再余弦函数在第二象限为减函数，有α＜β得

分析：应用两个角的三角函数的公式，依次求出α+β，α+2β的值。

分析：由函数 f（x）的单调性知自变量的值，列得方程组：，从而得观察该方程组与cos（α-β）之间的联系，将sinα+sinβ＝-sin 360与cosα+cosβ＝-cos360两边平方相加，得sin2α+sin2β+2 sinαsinβ+cos2α+cos2β+2 cosαcosβ＝1结合公式 cos（α-β）＝cosαcosβ+sinαsinβ，可得其值为

分析：先化简函数式子，再确定周期等。

练习

一、化简：

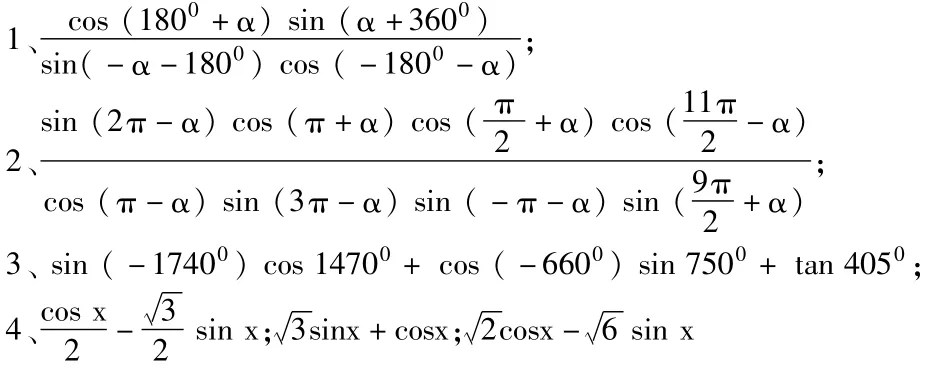
二、求值：

通过以上练习，里边总是蕴含着同角三角函数式的变换，两个角的函数式的变换等三角变换。

代数公式、三角公式（或者说“代数恒等变换、三角恒等变换”）皆是“只变其形不变其质”的。

变换是数学的重要工具。“只变其形不变其质”的三角变换，揭示外形不同但实质相同的三角函数式之间的内在联系。三角变换包括变换的对象，变换的目标，变换的依据和方法等要素。两角和与差的正弦、余弦和正切公式就是三角变换的基本依据。通过对这些公式的探求，以及利用这些公式进行三角变换，我们将在怎么样预测变换目标，怎么样选择变换公式，怎么样设计变换途径等方面作出思考，从而训练和提高了我们的思考能力、推理能力、运算能力。

思维有序性和表述条理性是三角变换的基本要求。

最后，概括一下代数变换和三角变换的关系，以加深对三角变换的认识：

代数式变换往往着眼于式子结构形式的变换。对于三角变换，由于不同的三角函数式不仅会有结构形式方面的差异，而且还会有所包含的角，以及这些角的三角函数种类方面的差异，因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系，并以此为依据选择可以联系起来它们的那个恰当公式，这是三角式恒等变换的重要特点。