稠油油藏水平井冷采试井数学模型研究
2018-11-15孙玉豹熊书权林珊珊张卫行
周 明,孙玉豹,熊书权,林珊珊,张卫行,姬 辉
(1.中海石油(中国)有限公司深圳分公司恩平油田作业区,广东深圳 518000;2.中海油田服务股份有限公司油田生产事业部,天津 300459)
矿场大量实践表明,由于流体黏度较大,稠油油藏冷采中的渗流不符合经典达西定律,存在启动压力梯度。目前国内外对水平井试井解释理论的研究或者没有考虑启动压力梯度[1,2],或者建立的水平井试井数学模型采用数值方法求解[3]。本文在前人研究基础上,基于源函数方法,建立存在启动压力梯度的水平井试井数学模型,并利用Newman乘积方法进行半解析求解,得到启动压力梯度对试井双对数曲线的影响规律。
1 稠油油藏水平井冷采物理模型分析
Newman乘积方法实际上是数学物理方法中的一种降维方法,它可将一个三维的定解问题等价分解成一维或二维的问题,只要满足以下两个条件:(1)分解后的三个一维问题(或一个一维问题和一个二维问题)中的源在空间上的交集(公共部分)应为原三维定解问题中的源形状;(2)三个一维问题(或一个一维问题和一个二维问题)中的外边界所包含的空间的交集(公共部分)应为原三维定解问题中的外边界所包含的空间。
因此,利用Newman乘积方法可将水平井试井井底压力求解这个三维问题转化为一个板源函数和一个线源函数的叠加(见图1,图2)。

图1 板源函数示意图

图2 线源函数示意图
板源函数的宽度为水平段的长度2L(见图1),板源函数的外边界假设可根据油藏实际情况做不同处理。无限大板源由无穷多的平面源组成,可由叠加原理而得到,表面圆柱源可视为一条线源绕一轴旋转而得到。
线源函数由两个无限大面源函数叠加得到(见图2),外边界假设可根据油藏实际情况做不同处理。根据存在启动压力梯度时压力叠加方式的论述[4],启动压力梯度只在线源函数中考虑。
2 稠油油藏水平井冷采源函数的建立及求解
通过上节的论述,存在启动压力梯度的稠油油藏水平井冷采压力响应源函数被归结为一个板源函数和一个存在启动压力梯度线源函数的叠加,即:
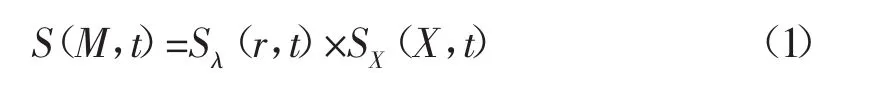
式中:S(M,t)-存在启动压力梯度的稠油油藏水平井冷采压力响应源函数;SX(X,t)-对应的板源函数;Sλ(r,t)-对应的存在启动压力梯度线源函数。
2.1 板源函数的确定
板源函数的各种形式在文献中已有列出[5],本文采用无限大板源函数,定义如下:

2.2 线源函数的确定
对于二维问题,由源函数求取压力变化分布Δp(M,t)的定义式为:

式中:pi-原始地层压力,atm;p(M,t)-压力分布,atm。
其两端对t求导,并转换为径向坐标,得:

所以得到已知压力分布时点源函数的确定公式:

为求压力分布,建立存在启动压力梯度的稠油油藏复合储层试井数学模型(见图3),假设条件如下:
(1)单相微可压缩液体;(2)等温流动;(3)油井半径为rw,考虑表皮因子S的影响;(4)油井生产前,地层中各点的压力均匀分布,内区和外区均为pi;(5)忽略井储、重力、毛管力的影响;(6)线性非达西渗流,考虑启动压力梯度λ;(7)地层径向复合、等厚、各向同性,井以一常产量q生产;(8)地层岩石微可压缩。
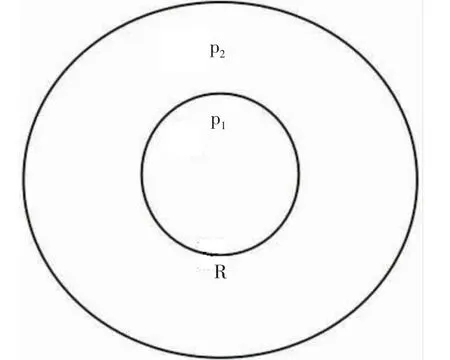
图3 稠油油藏复合储层示意图
无因次化后的数学模型为:

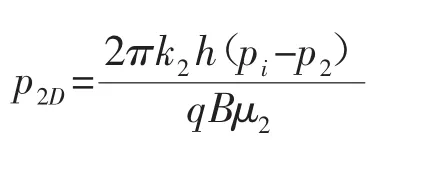

式中:k-有效渗透率,μm2;h-油层厚度,cm;p-压力,atm;q-产量,cm3/s;B-体积系数,无因次;rwe-等效井径,cm,rwe=rwe-S;rw-井筒半径,cm;S-表皮因子,无因次;λ-启动压力梯度,atm/cm;R-内区半径,cm;R'-无因次化后的R,cm;下标1、2-内区、外区。
内区和外区对应的Laplace空间压力分布为:



利用无因次定义式和Stehfest数值反演[6]将Laplace空间压力分布转化为实空间压力分布p1、p2后,按照(5)式所列方法,可求得对应存在启动压力梯度的线源函数 Sλ(r,t)。

联立(1)、(2)、(6)式,得到存在启动压力梯度的源函数。按照(3)式对源函数进行积分即可求取实空间不考虑井储的压力变化分布。再对压力分布进行数值离散、Laplace数值变换,利用杜哈美原理即可得到Laplace空间考虑井储的压力分布。再次使用Stehfest数值反演,即可得到实空间考虑井储的压力分布。
3 启动压力梯度试井响应规律分析
选取典型的稠油油藏水平井冷采基础参数(见表1),利用本文求得的稠油油藏水平井冷采井底压力解,对启动压力梯度试井响应规律进行分析。

表1 存在启动压力梯度水平井冷采基础参数表
启动压力梯度考虑10-3MPa/m、10-4MPa/m、10-5MPa/m三个水平,得到了对应的压力-压力导数双对数曲线(见图4)。分析图4,启动压力梯度对水平井冷采压力响应的影响规律表现为:主要影响测试中期、后期;启动压力梯度越大,压力-压力导数曲线后期数值越大,压力导数和压力曲线后期上翘越明显。
4 结论
(1)利用Newman乘积方法,将稠油油藏水平井冷采的源函数归结为一个板源函数和一个线源函数的叠加,利用不同外边界的板源函数和线源函数,即可构造出对应外边界条件的水平井冷采源函数。
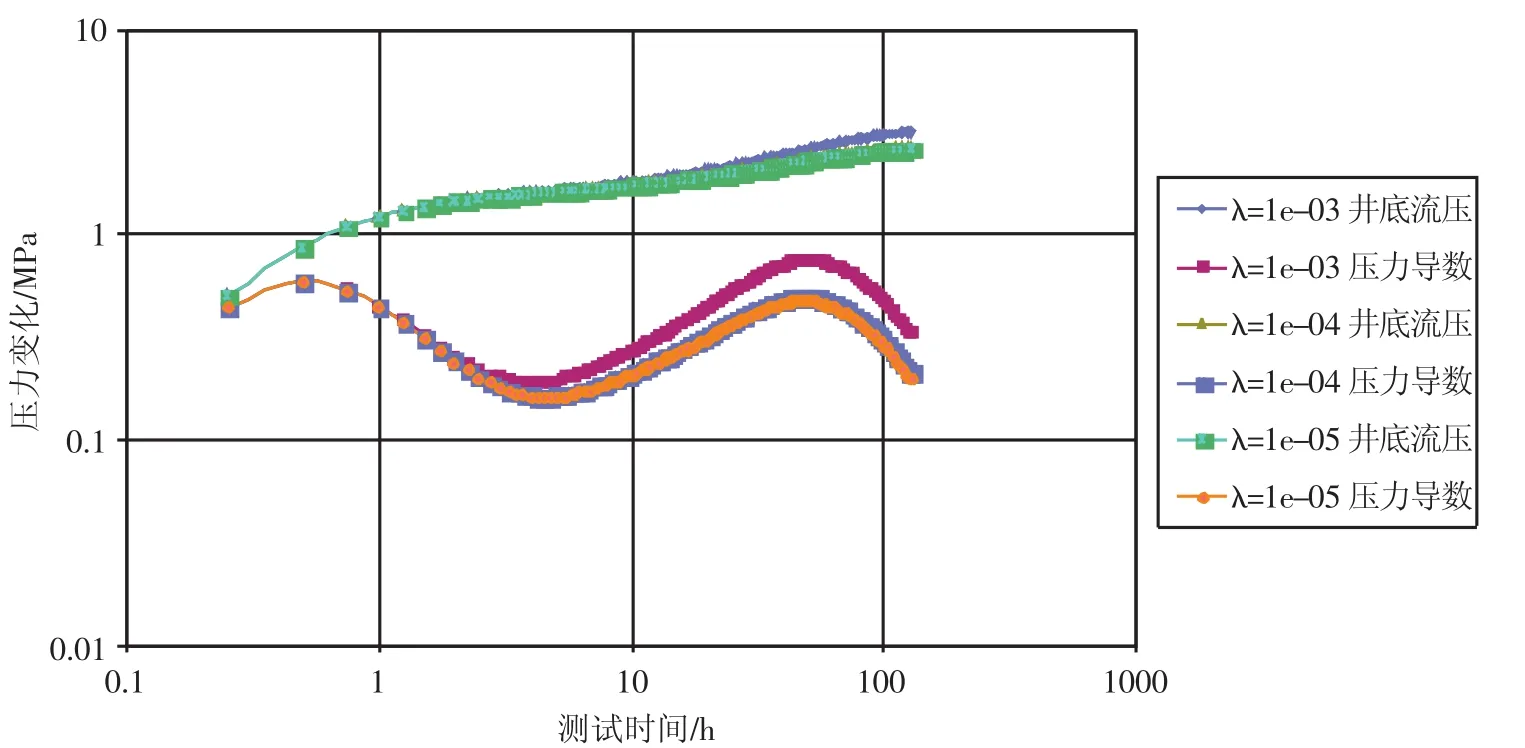
图4 不同启动压力梯度压力-压力导数曲线
(2)建立了存在启动压力梯度的线源函数,并利用Laplace数值变换、Stehfest数值反演、杜哈美原理等工具,可以方便地实现水平井压力分布的半解析求解。
(3)通过分析不同启动压力梯度稠油油藏水平井冷采压力响应规律,发现启动压力梯度越大,其对压力-压力导数曲线后期的影响越明显,压力-压力导数曲线后期上翘幅度越大。
