利用开普勒定律研究抛物线轨迹天体的运动时间——以第34 届全国中学生物理竞赛复赛试题第2题为例

蒲存瑶 李 裔 杨 浩 兰小刚

(西华师范大学物理与空间科学学院,四川 南充 637002)

1 引言

天体运动及相关知识是物理竞赛的考察重点之一,涉及椭圆、抛物线、双曲线等多种运动轨迹.[1,2]这其中由于椭圆具有很多特殊性质,因此处理椭圆轨迹天体运动时间的途径比较灵活多变,学生也较为容易提出解决方案.但对于抛物线轨迹天体,由于此类曲线不闭合,求解其运动时间则相对复杂些.往往需要借助微、积分等高等数学方法:首先求出位移与时间的微分关系,再对时间和位移分别积分.该方法对中学生来说是比较困难的.[3,4]接下来,我们以2017年第34 届全国中学生物理竞赛复赛试题第2题为例,先简要介绍下利用积分求解抛物线轨迹天体运动时间的方法.再详细介绍我们提出的一种基于开普勒定律,运用初等数学知识,求解抛物线轨迹天体运动时间的方法.

2 题目

(a) (b)

(1) 彗星先后两次穿过地球轨道所用的时间;

(2) 彗星经过C、D两点时速度的大小.

已知积分公式

-2a(x+a)1/2+C,

式中C是任意常数.

解法1:由于彗星的运动轨道为抛物线,其具有偏心率为1,机械能为0的性质,即

ε=1,E=0.

(1)

故彗星绕太阳运动的轨道方程为

(2)

根据彗星绕太阳运动过程中机械能守恒,[5]可得

(3)

(3)式中,V(r)=-GMm/r为系统的引力势能.

当彗星运动到近日点A时,其径向速度为0.设其到太阳的距离为rmin,由(3)式得

(4)

由(4)式及题设条件,可得近日点距离为

(5)

由(3)式还可得到

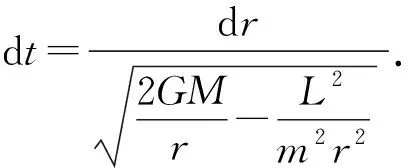
(6)

设彗星由近日点A运动到与地球轨道的交点C所需得时间为Δt,对(6)式两边积分,并利用(5)式得

(7)

对(7)式应用题设给出的积分公式,可得

(8)

便可求得彗星由近日点A运动到C点所用时间,其中RE、G、M皆为已知常数,最后根据对称性分析,可知彗星两次穿过地球轨道所用的时间为T=2Δt≈6.40×106s.

3 进阶研究

上述求解方法要求学生必须具备一定的微积分知识,且积分过程比较繁琐.尽管在题设中已给出相关不定积分公式,但由于本题求解过程和涉及的表达式较为复杂,学生在解题过程中很难得到与参考公式形式一致的不定积分公式.此外,就解题思路而言,绝大多数中学生也不习惯采用此类分析方法.接下来,我们提出一种基于开普勒定律,结合初等数学知识,处理此类问题的方法.

首先,由开普勒第二定律可知:行星与太阳的连线(矢径)在相等的时间内扫过相等的面积,[6]即vrsinθ=常数.因此,可利用彗星先后经过地球轨道上(C、D两点),并相对太阳所扫过总面积Se与彗星单位时间扫过面积Sv的比值,来计算彗星先后经过地球轨道所用时间Δt.

如图1(b)所示,彗星经过C、D两点相对太阳扫过面积,可视为抛物线弓形区域面积(S△eDA)与三角形CDS面积(S△CDS)之差,即

Se=S△eDA-S△CDS.

(9)

由阿基米德抛物弓形面积算法可知:[7]对于任意抛物线,若A是顶点,CD是垂直于对称轴的弦,则抛物线与弦CD围成弓形的面积就是△CDA面积的4/3倍.具体到本题中,即

其中

S△CDA=AE·CE,S△CDS=SE·CE.

(10)

令∠CSA=α,则SE=CS·cos(π-α)=-REcosα,将A、C点位置矢量代入曲线方程,可得cosα=k/RE-1.由此可得到以下关系

(11)

由(9)～(11)式,得出

(12)

(13)

由(12)、(13)式求得彗星先后两次穿过地球轨道所用时间为

(14)

代入相关数据,得出结果Δt≈6.40×106s.

4 总结

天体运动一直是高中物理竞赛的考察热点.但对于沿抛物线轨迹运动的天体,学生往往觉得比较棘手.其中一个重要的原因就是:对于抛物线这类非闭合曲线,学生缺乏足够的高等数学知识,来研究此类天体的运动规律.本文中我们提出了一种研究抛物线轨迹天体运动时间的方法,在求解过程中,充分的运用了中学生熟悉的开普勒定律,也不会涉及微、积分运算.本方法为研究抛物线轨迹天体的运动规律提供了一种新思路.

此外,原参考答案中的第(3)式的表述形式,容易让学生产生误解:是否可以将动能表示为径向分量与切向分量的形式?但实际上,动能是标量,不能够分解.因此我们建议先将该式表示为

(15)

再分别把径向速度和切向速度代入上述表达式,得到相关结果.这样显得更为严谨.