2018年北京高考物理第24题解析及其教学启示

2018-11-15吴广国

物理教师 2018年10期

吴广国邹斌

(1. 北京景山学校,北京 100006; 2. 中央民族大学理学院,北京 100081)

在普通高中物理课程标准(2017年版)中提出的物理课程基本理念,特别强调要注重体现物理学科本质,培养学生物理核心素养.并且新课程标准认为高中物理教学需要格外注重课程的时代性,关注科技进步和社会发展需求.反映当代科学技术发展的重要成果和科学思想,培养学生的社会参与意识和社会责任感.[1]2018年北京高考第24题以“中国天眼”世界上最大的单口径球面射电望远镜FAST为背景素材,[2]通过对相关知识的介绍,考查考生通过新情境获取信息,思考并解决问题的能力.

点电荷的电场强度与对应球面面积矢量的点积称为电场强度通量(简称电通量).在无源的球面上,电通量是一个守恒量.在此基础上,延伸到同一球面单位面积接收的来自天体电磁波功率与望远镜正对球面大小有关的思想,引导考生理解地球上不同口径的望远镜观测同一天体其接收的功率应该与它的接收面积成正比.最后与100m望远镜相比,其灵敏度大大提高,引导学生建立空间电磁辐射的物理模型,并从理论上大致预测FAST能观测到的目标天体的数目.试题设计巧妙,逐步引导考生领悟场和通量等基本物理概念.

1 2018年高考理综卷(北京卷)物理第24题原题

第24题原题如下.

(1) 静电场可以用电场线和等势面形象描述.

(a) 请根据电场强度的定义和库仑定律推导出点电荷Q的场强表达式;

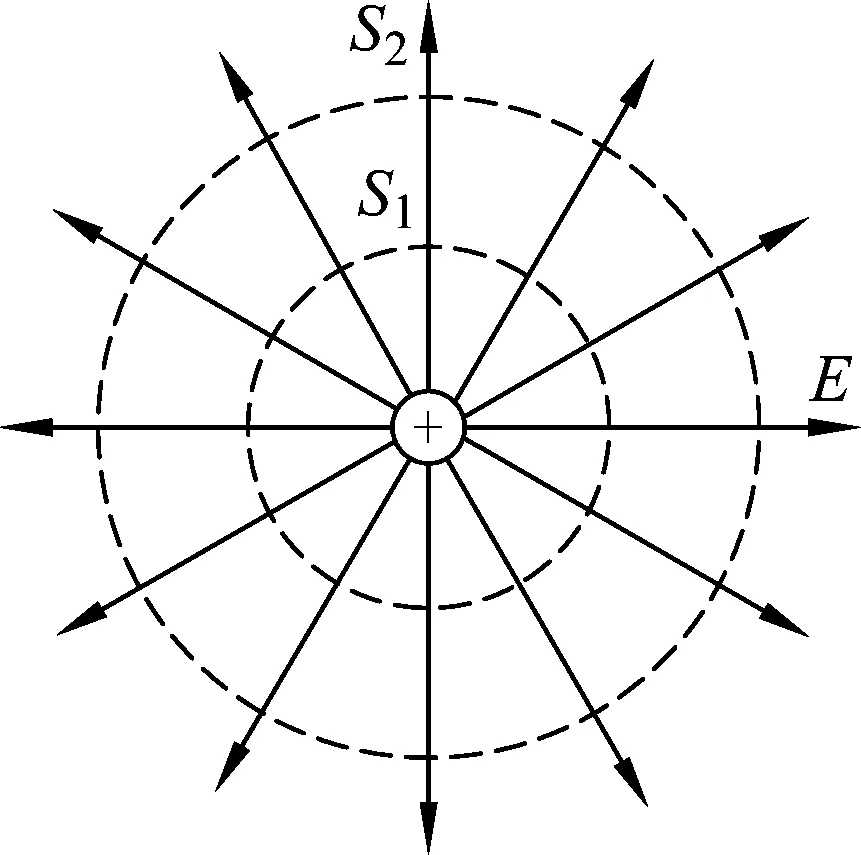
图1 正点电荷Q的电场线和等势面

(2) 观测宇宙中辐射电磁波的天体,距离越远单位面积接收的电磁波功率越小,观测越困难.为了收集足够强的来自天体的电磁波,增大望远镜口径是提高天文观测能力的一条重要途径.2016年9月25日,世界上最大的单口径球面射电望远镜FAST在我国贵州落成启用,被誉为“中国天眼”.FAST直径为500 m,有效提高了人类观测宇宙的精度和范围.

(a) 设直径为100 m的望远镜能够接收到的来自某天体的电磁波功率为P1,计算FAST能够接收到的来自该天体的电磁波功率P2;

(b) 在宇宙大尺度上,天体的空间分布是均匀的.仅以辐射功率为P的同类天体为观测对象,设直径为100 m望远镜能够观测到的此类天体数目是N0,计算FAST能够观测到的此类天体数目N.

2 对2018年高考理综卷(北京卷)物理第24题的解析和评述

(1) (a) 在距Q为r的位置放一电荷量为q的检验电荷.根据库仑定律检验电荷受到的电场力

(1)

由电场强度的定义

(2)

得

(3)

(b) 直观的解答方法:因为球对称,所以穿过两球面的电场线的条数相等,设为N0,则穿过两等势面单位面积上的电场线条数之比

(4)

深究本小问的物理科学本质,该小问十分巧妙地考查了电场强度通量(以下简称电通量)这一物理概念.

首先,高中物理教学一般会向学生介绍磁通量这一概念,并且考生也应该知道通过某一平面的磁通量的大小,可以用通过这个平面的磁感线的条数的多少来形象地说明.高中所讲的面积是平面的面积,磁场也是匀强磁场.类比于磁通量的概念,我们同样也可以用通过某个平面的电场线的条数多少来形象地描述通过该平面的电通量的大小.

其次,虽然本题的电场强度不是匀强电场,并且面积还是球面面积,但是题目巧妙设定了正点电荷激发的电场,由球对称性可知这种电通量正好等于电场强度大小乘以相应位置球面的面积.注意电场强度和面积都是矢量,电通量为这两个矢量的点乘,考虑球对称性,矢量点乘可以变成标量乘积的形式.则单位面积上通过的电场线条数与该点对应的电场强度大小成正比.所以利用第(3)式,该小问又可以解答为

(5)

需要说明的是,利用真空中静电场的高斯定理

(6)

可以计算闭合曲面电通量.由该定理可以很明显地看出,(4)式中穿过闭合球面的电场线条数正比于球心处的点电荷Q大小除以真空中的介电常数,即

(7)

所以教师可以从高斯定理入手,深刻理解(4)式的计算过程,挖掘其物理学科的本质.

(2) (a) 设直径为d=100 m望远镜,FAST望远镜的直径D=500 m.设该天体辐射功率为P0,该天体到地球望远镜的距离为L.一般可以认为天体辐射的波前为球面,来自某天体的电磁波到达地球时单位面积上的辐射功率乘以望远镜的“物镜”面积,就是望远镜能够接收到的功率,即

(8)

(9)

所以

(10)

即P2=25P.

(b) 探测器在探测信号时都有一个测量阈值,即单位时间内接受到的能量为Pt,望远镜接收到的功率小于该阈值Pt将不会被探测到.2018年高考理综卷(北京卷)的考题提到,“为了收集足够强的来自天体的电磁波,增大望远镜口径是提高天文观测能力的一条重要途径”,也就是说题目主要考虑增大望远镜口径这种单一因素来提高仪器的观测能力,默认两种望远镜的测量阈值相同.

图2 正入射的天体A和斜入射的天体B示意图

题干设宇宙大尺度,天体的空间分布均匀,并仅考虑辐射功率为P的同类天体.这样的理想化描述意味着在计算第(2)问全过程中都需要假设,在宇宙大尺度上天体辐射能量不会衰减,且不考虑广义相对论的影响.

设d=100 m的望远镜面积为S0,直径D=500 m的FAST望远镜的面积为S,设能够刚好探测到的天体A(正对于望远镜“物镜”的天体,如图2所示)到两个望远镜的最大距离分别为L0和L. 对于直径为d=100 m的望远镜的测量阈值为

(11)

同样,对于直径D=500 m的望远镜,其测量阈值为

(12)

由题意分析知,两种望远镜的测量阈值相同,有

(13)

所以

(14)

考虑望远镜可以适当转向所要观测的空域,并且地球是在不断的自转.这样,即使原本不正对望远镜的天体B可以通过适当的办法让它正对望远镜.在一定的时间范围内(比如说1天),我们可能实现对宇宙全空间的探测(以望远镜为球心,立体角为4π).此时,一个望远镜能观测到的此类天体数目正比于以望远镜为球心、以最远观测距离为半径的球体体积(这是非常理想的情况).即能够探测到的宇宙空间体积之比为

(15)

考虑在宇宙大尺度上天体的空间分布是均匀的,有

(16)

得N=125N0.

对上述结果我们可以作如下两个方面的进一步探讨.

① 南仁东教授在“FAST 的进展”一文中提到位于北半球的FAST的天顶角为40°.[2]即使考虑地球自转的运动,实际上FAST也很难做到对全空域进行观测.在这种情况下,FAST观测的空域体积与其所能观测的最大距离L是什么关系呢?

我们暂时仅考虑地球自转的情况.考虑到地球自身的半径远远小于L,所以可以把地球看成一个质点,作为球坐标系的原点.这里我们以地球赤道平面为球坐标系的xOy面,以指向北极星的地轴为z轴正方向,如图3所示.考虑到望远镜可以在地球经线方向上作适当的调整,以利于观测,所以在剖面图上望远镜的测量范围可以认为是一个扇形,如图3中阴影部分所示.我们不妨假设FAST能探测到的同类天体位于球函数坐标β≤θ≤γ范围内,用Matlab软件可以画出立体示意图,如图4所示.在图4中,各坐标轴上的数值均以L为单位.

在球坐标系下很容易计算出,这种情况下FAST观测的空域体积为

(17)

由上式可以看出,β≤θ≤γ范围基本不变的情况下,观测的空域体积与最大距离L3次方成正比.

图3 地球自转使得FAST能探测到的空域剖面图

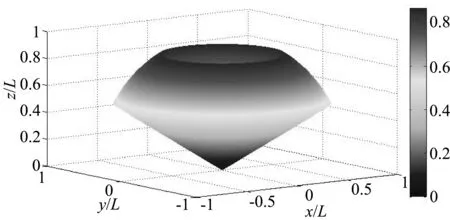
图4 地球自转使得FAST能探测到的空域立体示意图

即使进一步考虑地球公转的因素,因为地球的公转轨道半径依然远远小于FAST观测的最大距离L,所以还是可以把绕太阳公转的地球看成质点,上述推导过程和结论保持不变.

② 如果认为望远镜是静止的,即不考虑望远镜适当可以转向和地球的运动,或者考虑在很短的观测时间内(如1min内),望远镜还没有调整观测方向,此时望远镜能观测到的同类天体的范围是什么样的,其对应的体积还与L3或者L03成正比吗?

为此我们以FAST观测为例,假设有一辐射功率也为P的天体B相对FAST不是正对的. 同样不考虑广义相对论的影响,相对于辐射天体B的望远镜“物镜”平面的有效平面面积为Scosα,如图2所示.则在同样距离下,FAST接收到的来自于天体B和天体A辐射功率是不相同的.可以大致判断出来,随着α角的增大,望远镜能够观测到的辐射功率均为P的最远天体的距离在减小.

以下简略地给出这种理想情况下FAST可以观测到的天体范围和数目.考虑到天体A在FAST的正上方,距离设为L,天体B在其斜上方,到FAST的距离设为l.天体A和天体B均为FAST所能探测到的最远同类天体.则有

(18)

整理得

L2cosα=l2.

(19)

设FAST所在的位置为坐标原点,其正上方为z轴正方向,望远镜“物镜”平面为xOy面,在图2中设向右为y轴正方向.我们不妨先在yOz平面讨论问题,由几何关系可以看出,当y>0,z>0时B的坐标与距离l的三角函数关系为

y=lcosα,z=lsinα.

(20)

且有

(21)

将(20)式中的两式平方并相加,然后与(21)式一起代入(19)式中,整理得到

(22)

利用Matlab软件画出(22)式的函数曲线,如图5所示.

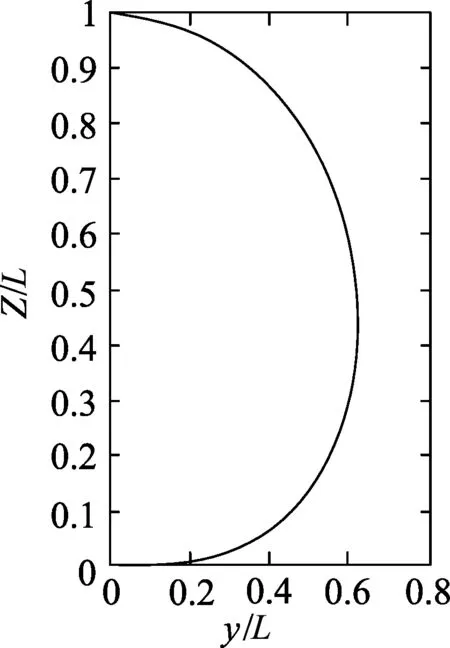
图5 静止的FAST所能探测到最远天体范围的二维剖面图

假设FAST静止,其探测的同类天体相对于z轴为旋转对称的.所以静止的望远镜能观测到的辐射功率P的同类天体最远范围为类似一个鸡蛋形状的立体图形,如图6所示(利用Matlab软件绘制).在图6中,FAST处于坐标原点处,各坐标轴上的数值均以L为单位.

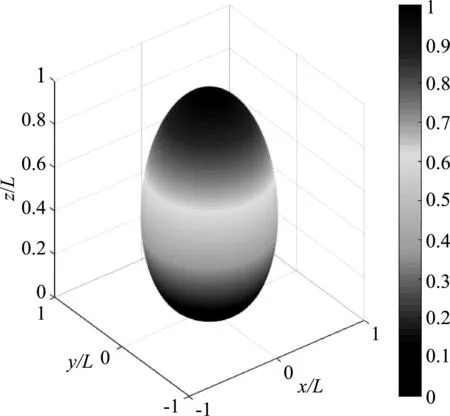
图6 静止的FAST看到的具有相同辐射功率的最远天体范围示意图

考虑对称性,图6的立体图形在某个z高度的切面为圆形,圆的半径r可以由(22)式给出

(23)

则最远天体范围的体积可以通过积分得到

(24)

即该体积依然与L3成正比,(16)式中N=125N0的结论依然是成立的.

由以上的讨论中可以看出,如果孤立的、静止的看待望远镜探测问题,将使第(2)题(b)的解答过程陷入困境,相关数学工具可能也是高中学生并不掌握的.只有考虑望远镜可适当进行调节,并且假设望远镜可以进行全空域的观测这种理想情况存在,将第(2)题(a)小问中以天体为几何中心转变为(b)小问中以望远镜为几何中心,转换解题思路,才能比较快速地解答2018年北京高考压轴题的最后一问.

3 教学启示和总结

本题第1问根据基本物理规律库仑定律和电场强度的定义来求解空间点电荷电场强度的表达式,题目较为简单.而电场线条数背后隐含着电场强度通量这一概念,这里更是用静电场的问题在隐含考查静磁场的相关概念.在教学过程中,特别要注意基本物理概念和规律的学习,引导学生多思考电场和磁场的异同点,深刻理解“场”这一重要的物理概念.

第2问(a)中,其实已经引导着我们得出,望远镜的面积变大,会使同一个天体辐射到达望远镜的功率变大.而作者认为(b)中最核心的信息为① 在宇宙大尺度上,天体的空间分布是均匀的,这就告诉我们天体个数与体积成正比; ② 望远镜等探测仪器探测到天体是有一个测量阈值,原来能有辐射到达小面积的望远镜而无法被探测到,面积大了以后,接收到的能量达到阈值后就能够被探测到,从而增加探测到的天体数目.

阈值的思想和概念在考试题目中并没有给出,对考生来说,这也是本题需要格外注意的地方.在日常的教学过程中,如何使学生能够理解并掌握这种物理本质?这不是通过做了多少题目能够训练出来的.比如我们在学电流时,知道有安培、毫安、微安、纳安甚至皮安等电流的单位,那如果我们用普通实验室的电流表能否测出1 nA的电流呢?显然对于任何测量仪器来说,有一个测量阈值的概念存在.再比如我们用欧姆表的×10 k挡位来测量电阻值约是10.0 Ω的电阻,显然该挡位的测量阈值偏高,所以我们才需要去换较小档位进行测量.

总之,在学生获得知识的过程中,特别要注重基本物理概念和物理规律的形成和建立的过程,深刻理解引入物理概念和规律的必要性.对于基本的物理实验器材和设备,要切实理清其根本原理和物理本质,这也是注重物理学科的时代性,关注科学前沿与科技进步的基础和前提.