谁知盘中题 道道皆辛苦——关于法拉第电磁感应定律应用的高考试题赏析

罗振国

(福建省泉州市石狮第一中学，福建 泉州 362700)

法拉第电磁感应定律是电磁学的核心内容,一直都是高考考查的热点与难点,然而近年来高考试题中出现了不少关于“盘”的试题,有法拉第圆盘、阿拉果圆盘、圆环等等．这些试题立意精巧,另辟蹊径,对考生的能力要求较高．考生如果没有认真分析和深入理解其中内涵,很难得分的．本文笔者将从电磁感应的重点关键词进行分类,试图寻找问题的本质区别,希望能对大家有所帮助．

1 谁是电源?

法拉第电磁感应定律中,电源是关键,只有找到了电源,区分了电路,我们才能有效地解题运算.下面这道例题将让我们领略一下电源与电路的关系．

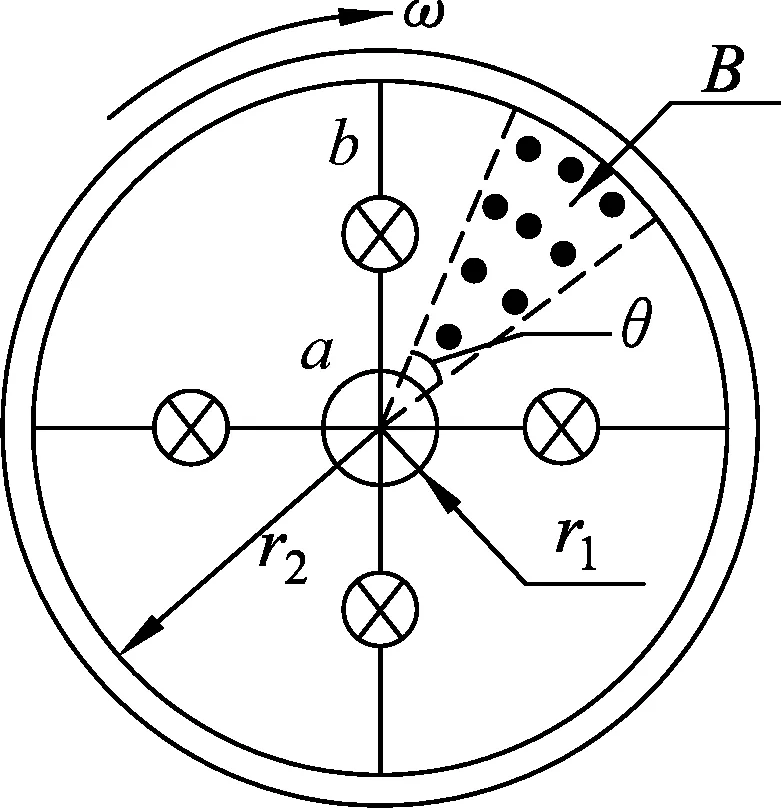
图1

例1.(2012年高考浙江卷第25题)为了提高自行车夜间行驶的安全性,小明同学设计了一种“闪烁”装置,如图1所示,自行车后轮由半径r1=5.0×10-2m的金属内圈、半径r2=0.40 m的金属内圈和绝缘辐条构成．后轮的内、外圈之间等间隔地接有4根金属条,每根金属条的中间均串联有一电阻值为R的小灯泡．在支架上装有磁铁,形成了磁感应强度B=0.10T、方向垂直纸面向外的“扇形”匀强磁场,其内半径为r1、外半径为r2、张角θ=π/6．后轮以角速度ω=2πrad/s相对于转轴转动．若不计其他电阻,忽略磁场的边缘效应．

(1) 当金属条ab进入“扇形” 磁场时,求感应电动势E,并指出ab上的电流方向;

(2) 当金属条ab进入“扇形” 磁场时,画出“闪烁”装置的电路图;

(3) 从金属条ab进入“扇形” 磁场开始,经计算画出轮子转一圈过程中,内圈与外圈之间电势差Uab-t图像;

(4) 若选择的是“1.5 V、0.3 A”的小灯泡,该“闪烁”装置能否正常工作?有同学提出,通过改变磁感应强度B、后轮外圈半径r2、角速度ω和张角θ等物理量的大小,优化前同学的设计方案,请给出你的评价．

答案：E=4.9×10-2V.

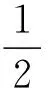
根据右手定则判断可知电流方向由b到a的．

图2

(2) 经过分析,将ab条可看做电源,并且有内阻,其他3根看做外电路,如图2所示.

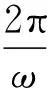
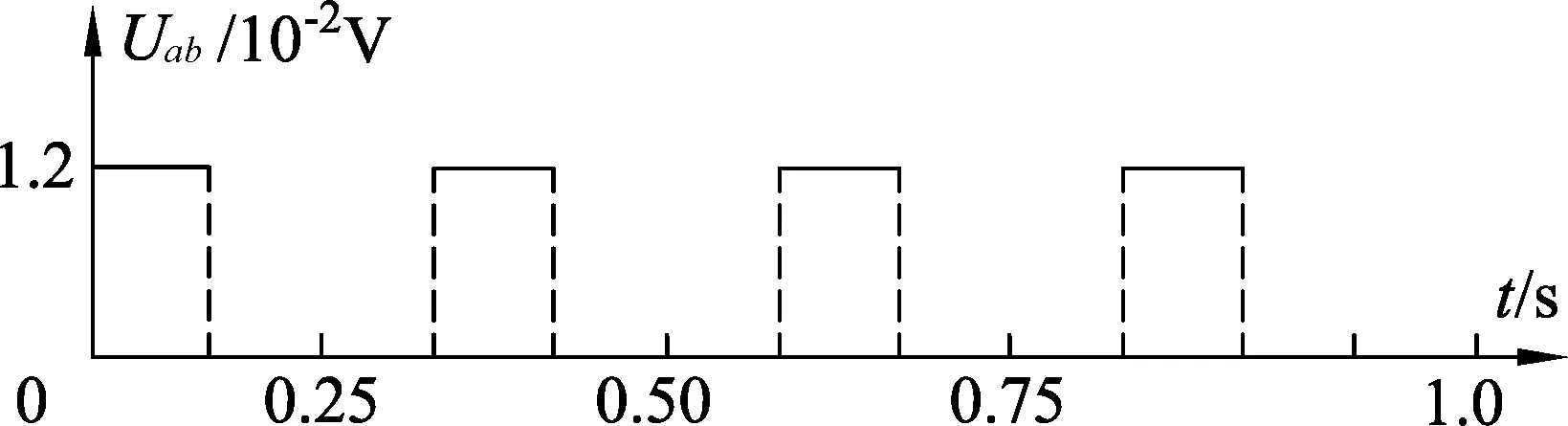
图3

(4) 小灯泡不能正常工作,因为感应电动势为E=4.9×10-2V，远小于灯泡的额定电压,因此闪烁装置不可能工作．

B增大,E增大,但有限度;r增大,E增大,但有限度;ω增大,E增大,但有限度;θ增大,E不增大．

2 正转反转不相同?

按理说,圆盘问题中正转与反转只能影响电流的方向,不会改变电源的大小,以及电流的大小,但是我们不能以偏概全,让我们看看下面这道高考试题．

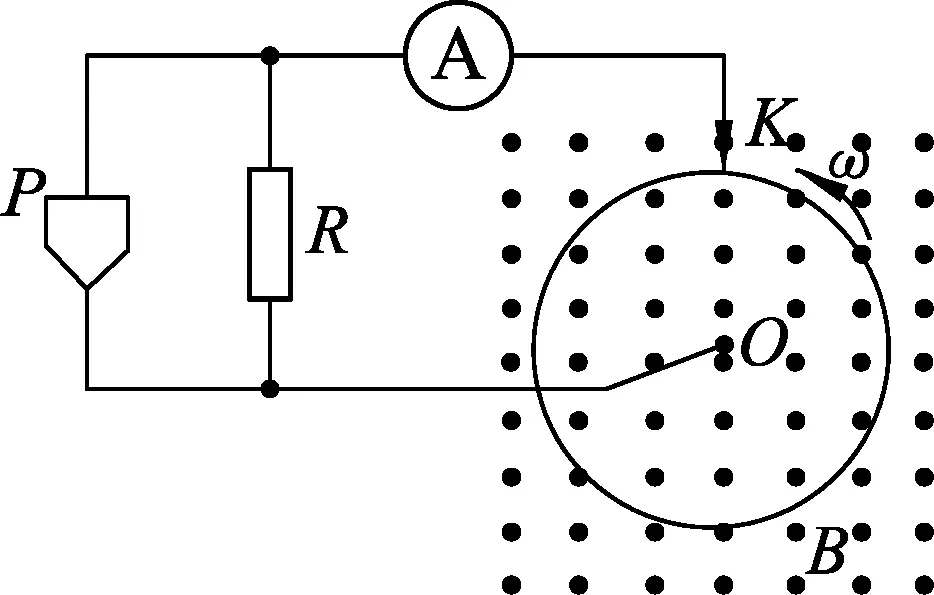
图4

例2.(2013年高考广东卷第36题)图4所示,在垂直于匀强磁场B的平面内,半径为r的金属圆盘绕过圆心O的轴承转动,圆心O和边缘K通过电刷与一个电路连接．电路中的P是加上一定正向电压才能导通的电子元件．流过电流表的电流I与圆盘角速度ω的关系如图5所示,其中ab段和bc段均为直线,且ab段过坐标原点．ω>0代表圆盘逆时针转动．已知R=3.0 Ω,B=1.0 T,r=0.2 m．忽略圆盘,电流表和导线的电阻．

(1) 根据图5写出ab、bc段对应的I与ω的关系式;

(2) 求出图5中b、c两点对应的P两端的电压Ub、Uc;

(3) 分别求出ab、bc段流过P的电流IP与其两端电压UP的关系式．

考点:电磁感应、欧姆定律、并联电路规律、直线两点式.

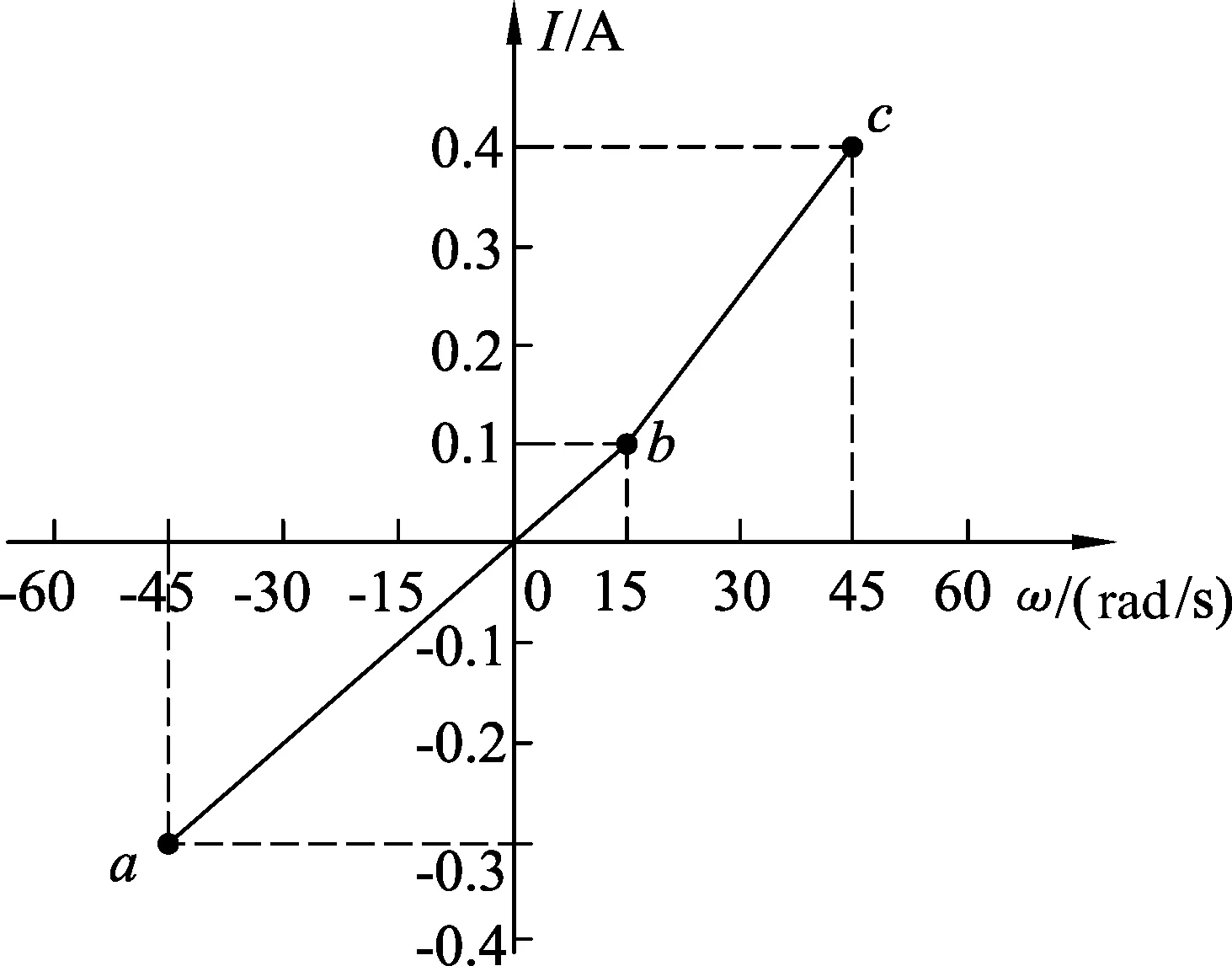
图5

解析: (1) 图像得出3点坐标:O(0,0)，b(15,0.1)，c(45,0.4).

由直线的两点式得I与ω关系式

当ω=15 rad/s时,产生的电动势为E=0.02×15 V=0.3 V．

当ω=45 rad/s时,产生的电动势为E=0.02×45 V=0.9 V．

忽略圆盘电阻即电源忽略内阻,故UP=E,可得

Ub=0.3 V,Uc=0.9 V．

(3) 由并联电路知识有

I=IP+IR.

(1)

(2)

我们会发现,正转与反转的原因使得电路中电流发生变化,单向导通的电子元件受到很大的影响,何况该电子元件还需要一定的正向的电压才能导通,因此使得整个电路的工作环境受到很大的制约．

3 谁让它转?

1824年,法国科学家阿拉果的“圆盘实验”让这个神奇的磁针转动起来了,然而到底是谁让它转起来了呢?这个问题困扰了当时科学家很多年．英国物理学家法拉第从1825年开始研究这个实验,直到1831年前后经历了6年时间才弄清了这个问题,证实了法拉第电池感应定律的正确性,足以说明这里面的曲折艰辛之处,要弄清这个问题非得下一番功夫不可．

图6

例3.(2015新课标Ⅰ-19)1824年,法国科学家阿拉果完成了著名的“圆盘实验”,实验中将一铜圆盘水平放置,在其中心正上方用柔软细线悬挂一枚可以自由旋转的磁针,如图6所示,实验中发现,当圆盘在磁针的磁场中绕过圆盘中心的竖直轴旋转时,磁针也随着一起转动起来,但略有滞后,下列说法正确的是

(A) 圆盘上产生了感应电动势.

(B) 圆盘内的感应电流产生的磁场导致磁针转动.

(C) 在圆盘转动的过程中,磁针的磁场穿过整个圆盘的磁通量发生了变化.

(D) 圆盘中的自由电子随圆盘一起运动形成了电流,此电流产生的磁场导致磁针转动.

答案： (A)、(B).

考点： 电磁感应现象;磁通量;涡流.

解析： 因为当磁体和导体之间的相对运动在导体内产生出了感应电流,而感应电流产生的磁力又会与磁体的磁力相互作用,从而使磁体一起转动起来,具体是当铜圆盘在小磁针的磁场中转动时,半径方向的金属条在切割磁感线,发生电磁感应现象,在铜圆盘的圆心和边缘之间产生感应电动势,选项(A)正确.圆盘在径向的辐条切割磁感线过程中,内部距离圆心远近不同的点电势不等而形成感应电流即涡流(根据圆盘转向的不同以及磁极的不同,感应电流从轴心流向边缘或从边缘流向轴心),而感应电流产生的磁力又会与小磁针的磁力相互作用,从而使小磁针一起转动起来,故选项(B)正确.圆盘转动过程中,圆盘位置、圆盘面积和磁场都没有发生变化,故磁场穿过整个圆盘的磁通量没有变化,选项(C)错误.圆盘本身呈中性,不会产生环形电流,(D)错误．

4 磁场部分覆盖与全部覆盖不一样？接外电路与不接外电路不一样？

都不接外电路时,圆盘全部处在磁场中与圆盘部分处在磁场是有本质的区别．前者是有电压没电流,没有热量消耗,盘会做匀速转动;而圆盘部分处在磁场中,则该部分充当电压,其他部分充当电阻,形成回路,将有涡电流产生,引起能量损耗,圆盘做减速转动．同样道理,如果盘不接外电阻,也是属于有电压没电流,不会有热量消耗．如下面两个例题所示．

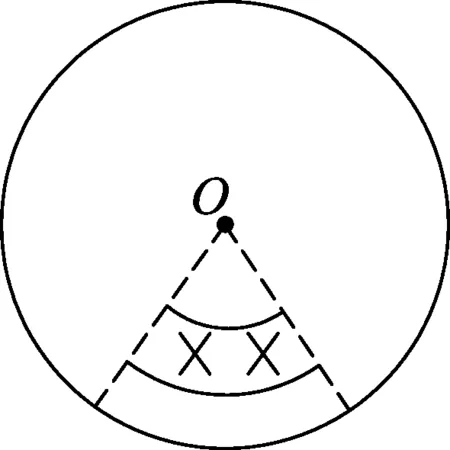
图7

例4.(2015年山东高考卷第17题)如图7,一均匀金属圆盘绕通过其圆心且与盘面垂直的轴逆时针匀速转动．现施加一垂直穿过圆盘的有界匀强磁场,圆盘开始减速．在圆盘减速过程中,以下说法正确的是

(A) 处于磁场中的圆盘部分,靠近圆心处电势高.

(B) 所加磁场越强越易使圆盘停止转动.

(C) 若所加磁场反向,圆盘将加速转动.

(D) 若所加磁场穿过整个圆盘,圆盘将匀速转动.

答案： (A)、(B)、(D).

解析： 由右手定则可知,处于磁场中的圆盘部分,靠近圆心处电势高,选项(A)正确.根据E=BLv可知所加磁场越强,则感应电动势越大,感应电流越大,产生的电功率越大,消耗的机械能越快,则圆盘越容易停止转动,选项(B)正确.若加反向磁场,根据楞次定律可知安培力阻碍圆盘的转动,故圆盘仍减速转动,选项(C)错误.若所加磁场穿过整个圆盘则圆盘中无感应电流,不消耗机械能,圆盘匀速转动．选项(D)正确.因此，选项(A)、(B)、(D)正确．

图8

例5.(2016年全国新课标Ⅱ卷第20题)法拉第圆盘发动机的示意图如图8所示.铜圆盘安装在竖直的铜轴上,两铜片P、Q分别与圆盘的边缘和铜轴接触.圆盘处于方向竖直向上的匀强磁场B中.圆盘旋转时,关于流过电阻R的电流,下列说法正确的是

(A) 若圆盘转动的角速度恒定,则电流大小恒定.

(B) 若从上向下看,圆盘顺时针转动,则电流沿a到b的方向流动.

(C) 若圆盘转动方向不变,角速度大小发生变化,则电流方向可能发生变化.

(D) 若圆盘转动的角速度变为原来的2倍,则电流在R上的热功率也变为原来的2倍.

答案： (A)、(B).

解析： 将圆盘看成无数幅条组成,它们都在切割磁感线从而产生感应电动势出现感应电流:根据右手定则圆盘上感应电流从边缘向中心,则当圆盘顺时针转动时,流过电阻的电流方向从a到b.

5 圆环与圆盘不一样?

圆盘与圆环看起来不一样,磁场覆盖的面积缺了一部分,但是圆盘与圆环都可以理解为旋转切割,匀速旋转时切割棒的速度是线性变化,我们可以用平均速度来等效替换,从而根据法拉第电磁感应定律E=BLv快速求解,所以从这个思维角度入手,圆盘与圆环是等价的．

图9

例6.(2014年高考全国2卷第25题)半径分别为r和2r的同心圆形导轨固定在同一水平面内,一长为r,质量为m且质量分布均匀的直导体棒AB置于圆导轨上面,BA的延长线通过圆导轨中心O,装置的俯视图如图9所示,整个装置位于一匀强磁场中,磁感应强度的大小为B,方向竖直向下,在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻(图中未画出)．直导体棒在水平外力作用下以角速度ω绕O逆时针匀速转动,在转动过程中始终与导轨保持良好接触．设导体棒与导轨之间的动摩擦因数为μ,导体棒和导轨的电阻均可忽略．重力加速度大小为g．求

(1) 通过电阻R的感应电流的方向和大小;

(2) 外力的功率．

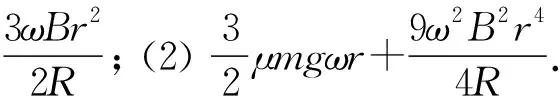
解析： (1) 在Δt时间内,导体棒扫过的面积为

(1)

根据法拉第电磁感应定律,导体棒产生的感应电动势大小为

(2)

根据右手定则,感应电流的方向是从B端流向A端,因此流过导体又的电流方向是C端流向D端.由欧姆定律流过导体又的电流满足

(3)

联立(1)—(3)式可得

(4)

(2) 在竖直方向有

mg-2FN=0.

(5)

式中,由于质量分布均匀,内外圆导轨对导体棒的正压力相等,其值为FN,两导轨对运动的导体棒的滑动摩擦力均为

Ff=μFN.

(6)

在Δt时间内,导体棒在内外圆导轨上扫过的弧长分别为

l1=rωΔt.

(7)

l2=2rωΔt.

(8)

克服摩擦力做的总功为

Wf=Ff(l1+l2).

(9)

在Δt时间内,消耗在电阻R上的功为

WR=I2RΔt.

(10)

根据能量转化和守恒定律,外力在Δt时间内做的功为

W=Wf+WR.

(11)

外力的功率为

(12)

由(4)—(12)式可得

(13)

解题点拨： (1) 掌握导体棒扇形切割原理; (2) 掌握电磁感应中等效电路的处理方法; (3) 掌握电磁感应现象中的能量转化分析．