风洞天平动态特性多阶惯性补偿技术研究

艾 迪, 许晓斌, 王 雄

(1. 中国空气动力研究与发展中心, 四川 绵阳 621000; 2. 中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室, 四川 绵阳 621000)

0 引 言

随着高超声速技术的发展，高超声速风洞中测量动态过程气动力的需求不断增多，对应变天平动态特性的要求也随之提升。如果测力系统振动频率落入气动力频域或附近，就会引起测力系统振动，导致天平信号中包含高频噪声和振动引起的惯性干扰量，影响应变天平动态测量精度。高频噪声可通过低通滤波器去除，因此，提高应变天平动态测量精度的关键是减少惯性力对天平测量结果的干扰。

目前，解决这一问题的方法主要是天平信号补偿，即将天平信号中的惯性力分量补偿掉。国内外学者广泛采用惯性补偿测力技术[1-5]，也有研究人员提出了数字补偿测力技术[6-8]，但尚未应用于风洞试验。惯性补偿就是在测力系统上安装加速度计，利用加速度信号解算出天平信号中的惯性力分量，然后从天平信号中扣除以得到真实气动力。目前较为普遍的补偿算法是将加速度信号乘以补偿矩阵得到惯性力分量，但由于测力系统的振动往往是多个不同频率振型的叠加，这种方法只能补偿信号中的主频分量，对非主频分量几乎无影响，限制了补偿精度进一步提高。

本文在传统的惯性补偿算法基础上，提出一种新的补偿策略：由于测力系统振动是由各阶主振动叠加而成，可将加速度计信号分解为各阶主振动信号(即模态分解)，然后分别对各阶主振动对应的天平信号进行补偿，最后将各阶补偿结果叠加得到最终的补偿结果，该补偿方法可称为“多阶惯性补偿方法”。

小波分析具有多尺度分辨率的特点[9]，常常用来对谐波信号进行检测和提取[10-12]。本文根据测力系统固有频率分布情况，采用离散小波变换和重构进行振动信号的模态分解。

为了理论研究的简便和直观，文献[13]将激波风洞的测力系统简化为固支的等截面悬臂梁模型。然而，对于常规高超声速风洞测力系统，模型的质量特性往往无法忽略，因此本文将尾支撑和天平简化为等截面悬臂梁，模型简化为悬臂梁自由端附加的集中质量。由于振动引起的惯性干扰量在实际结构中的分布与简化模型类似，可以通过简化模型定性地研究振动对气动力测量的干扰规律以及加速度惯性补偿技术。

本文首先采用理论方法阐述自由振动下各阶振型对气动力的干扰及分布规律，基于悬臂梁自由振型对应的气动力和加速度分布规律提出多阶惯性补偿方法，给出相应的“多阶惯性补偿公式”；进而通过数值软件仿真悬臂梁模型自由振动过程，采用离散小波变换得到各阶加速度分量，将其和理论补偿系数代入多阶惯性补偿公式，得到补偿结果，以检验多阶惯性补偿方法的可行性。

1 测力系统建模

高超声速风洞测力系统由模型机构、支杆、应变天平和飞行器模型组成，如图1所示。由于模型机构的刚度和质量远远大于其他部分，因此可以将模型机构与支杆连接视为固支，将支杆、应变天平和模型简化为带集中质量的等截面悬臂梁，如图2所示。天平可看作悬臂梁某截面，为了表述方便，悬臂梁截面的弯矩和剪力等效为天平信号中的俯仰力矩和法向力，并称为“气动力”。由于振动对法向力/侧向力和俯仰力矩/偏航力矩测量干扰更为突出，本文主要对悬臂梁的横向振动进行讨论。

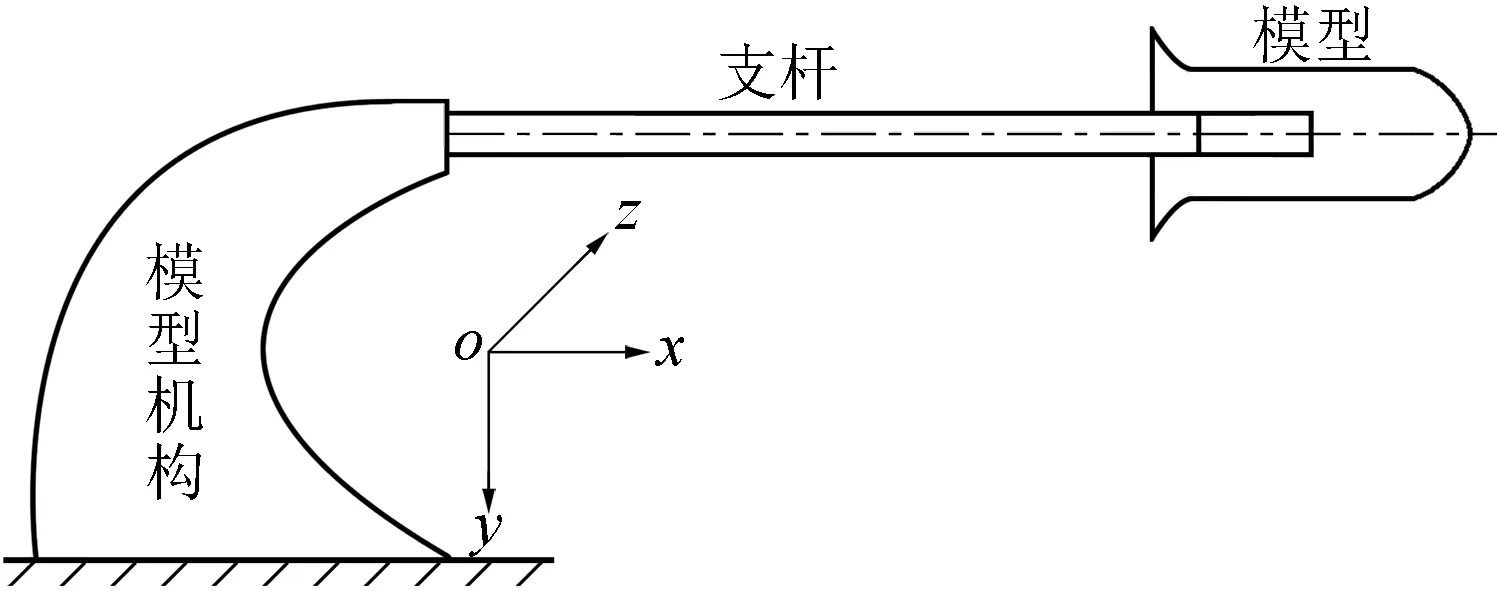
图1 风洞测力系统示意图

根据实际情况，本文对简化模型作如下合理假设：(1) 测力系统受力以及振动产生的变形均在线弹性范围内；(2) 由于有效试验时间较短，可忽略阻尼引起的振动衰减；(3) 测力系统振动幅值为小量，不影响实验模型姿态，并忽略流动和结构变形的耦合作用；(4) 支杆-天平结构实际长细比大于10，忽略剪切变形和转动惯量的影响，悬臂梁为欧拉-伯努利梁。

图2中规定悬臂梁固支点为原点o，轴向为x方向，长度为l，挠度为y(x,t)，弹性模量为E，截面中心矩为I，线密度为ρ，集中质量为m。

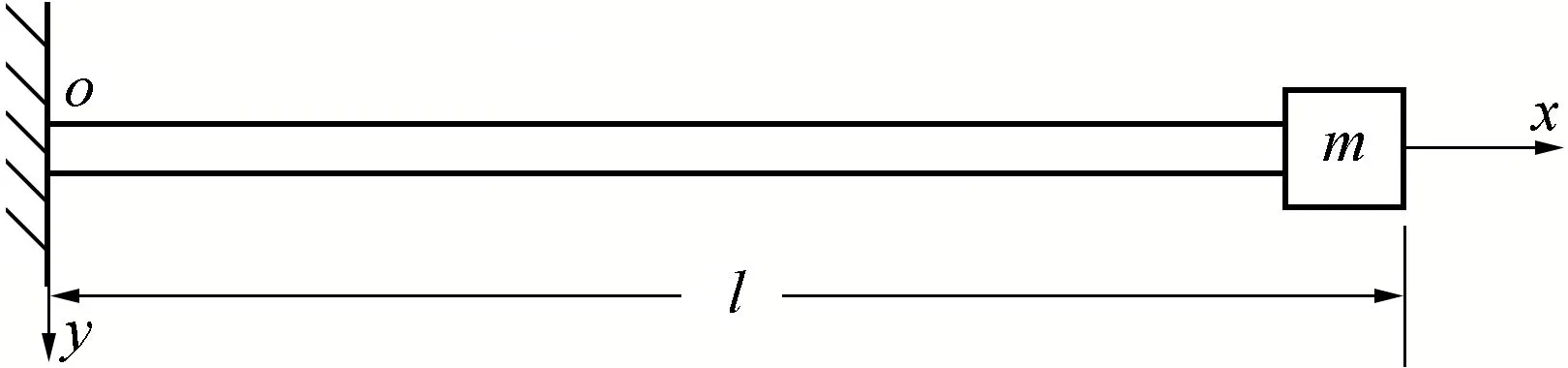
图2 带端部质量的悬臂梁模型

悬臂梁的自由振动方程为：

(1)

根据分离变量法，其通解[14]为：

y(x,t)=Y(x)r(t)

(2)

式中：

其中，Y(x)为主振型函数，r(t)为主坐标函数。

对于本文的悬臂梁模型，根据其边界条件得：

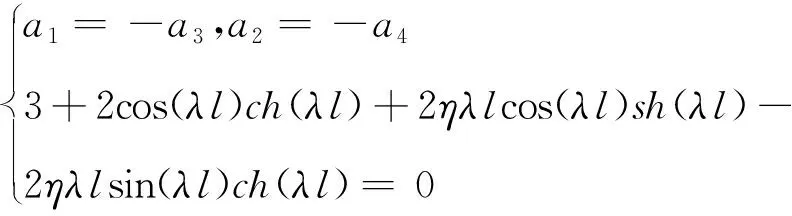
(3)

式中η=m/ρl，称为质量比系数。求解式(3)中的超越方程，可求得λi(i=1,2,3…)的值，则：

(4)

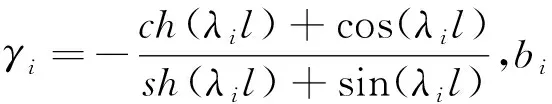
根据振型叠加法，悬臂梁系统的自由振动解可写为级数形式：

(5)

由式(5)可得，悬臂梁各地的俯仰力矩M、法向力Q和加速度A分别为：

(6)

2 自由振动惯性干扰分析与多阶惯性补偿方法

2.1 自由振动各阶振型的惯性干扰分析

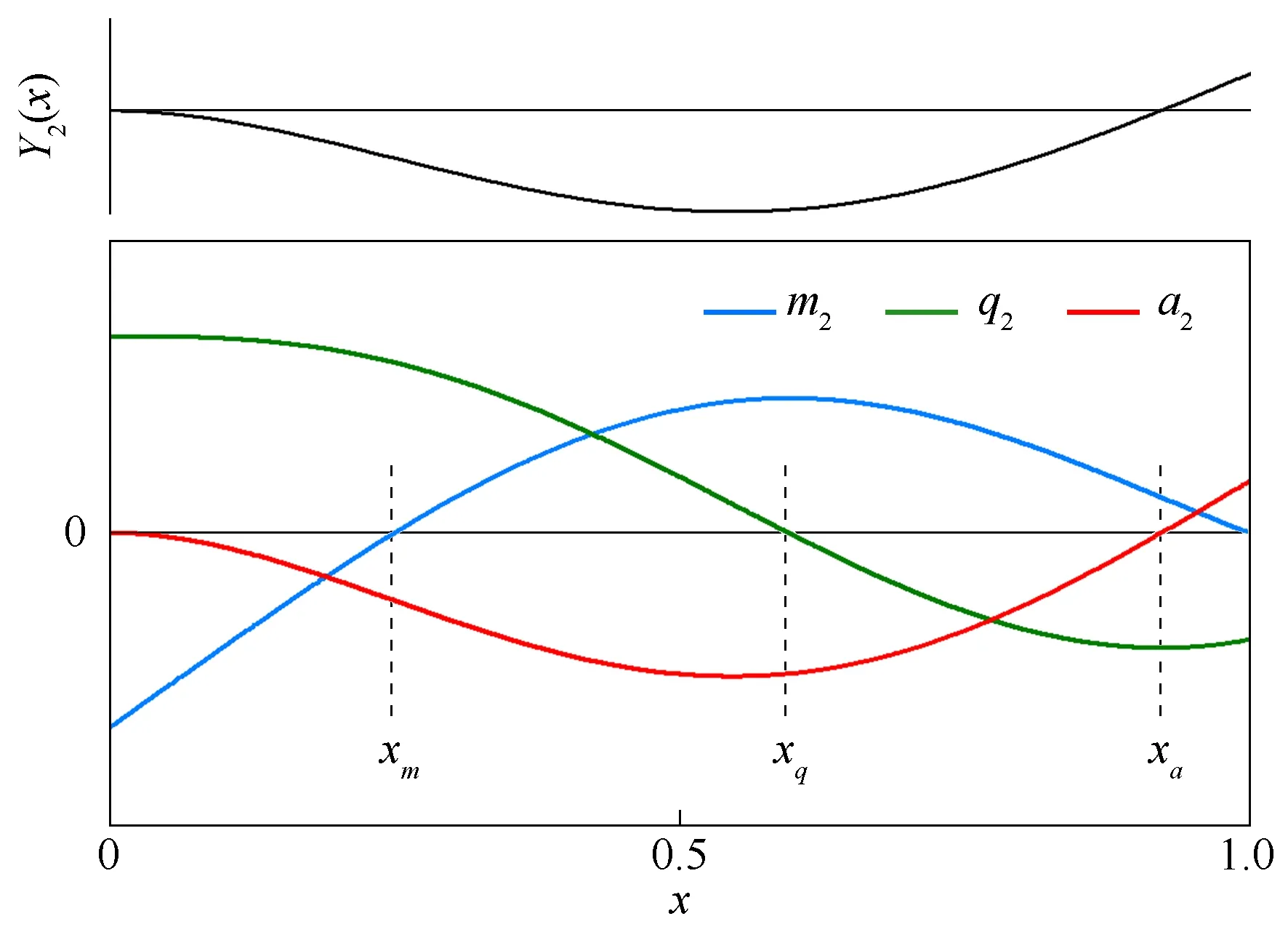
结合俯仰力矩、法向力和加速度的级数表达式(6)，得到自由振动第i振型对应俯仰力矩Mi、法向力Qi和加速度Ai为:

(7)

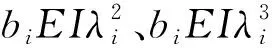
(8)

式中,mi、qi和ai只与λi有关，而从式(3)的超越方程可以看出λ取决于质量比系数η。

以常规高超声速风洞标模测力试验为例，标模质量和天平-支杆总质量之比约为1∶2，即η=0.5，其一、二阶主振型对应的俯仰力矩、法向力和加速度分布如图3所示。

(a) 一阶振型

(b) 二阶振型

图3 测力系统自由振动振型及对应的俯仰力矩分布mi(x)、法向力分布qi(x)和加速度分布ai(x)

Fig.3Forcemeasurementfreevibrationshapeandcorrespondingdistributionofpitchingmomentmi(x),normalforceqi(x)andaccelerationai(x)

分析图3可知：

(1) 对于第i阶振型，总存在i-1个非端部的“零点位置”。图3(b)中,x=xm、x=xq和x=xa分别为俯仰力矩、法向力和加速度的零点。若天平处于俯仰力矩或法向力的零点，则振动对天平俯仰力矩或法向力测量结果没有影响，原则上不需要进行补偿，或者补偿系数为零；如果加速度计处于零点位置，则加速度计无输出、无法对气动力进行补偿，为了避免发生这种情况，应使加速计安装避开各阶“零点位置”。

(2) 各阶振型对应的气动力和加速度分布并不一致，因此不同振型对应的气动力-加速度补偿关系也不相同。

传统惯性补偿方法是将加速度计(位置在x=xA)测量的加速度乘以一个补偿系数得到惯性力，然后与天平(位置在x=xB)所测得的气动力相加，得到消去惯性干扰的气动力，即:

(9)

式中,MT、QT分别表示传统方法补偿后的俯仰力矩和法向力；M、Q为原始俯仰力矩和法向力；KMA、KQA分别表示为俯仰力矩-加速度补偿系数和法向力-加速度补偿系数；A为加速度。

根据上述分析中的第2点，不同振型对应的加速度补偿关系并不一致，除非振动只包含单一振型，显然这与真实振动情况相违背。传统惯性补偿方法无法同时满足自由振动各阶补偿关系，反而会使某些振型的补偿出现错误，造成误差。

2.2 多阶惯性补偿方法

为了实现自由振动各阶振型差异化补偿，达到精确补偿的目的，本文提出多阶惯性补偿方法，具体内容如下:

设天平位置在x=xB处，加速度计位置在x=xA处，对于第i阶振型，补偿关系为:

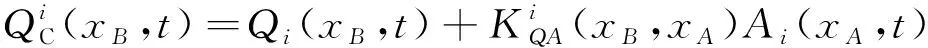
(10)

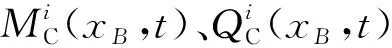
然后将各阶振型补偿后的气动力相加，可得补偿结果，即多阶惯性补偿公式:

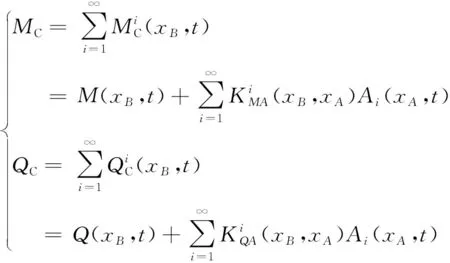
(11)

在自由振动中，输入的气动力为零，因此各阶振型补偿后的气动力也为零，即:

(12)

将式(12)和式(7)代入式(10)中，可得第i阶自由振型补偿系数为:

(13)

3 仿真验证

3.1 仿真验证方法

为了进一步说明多阶惯性补偿方法的可行性，本文采用有限元软件“ABAQUS”仿真悬臂梁受脉冲载荷激发冲激响应的自由振动过程。计算悬臂梁指定截面的弯矩、剪力和加速度作为天平和加速度计的输出，然后利用离散小波变换和重构分解加速度信号，最后代入多阶惯性补偿公式，得到多阶惯性补偿结果，其中补偿系数可由式(13)求得。

数值仿真采用的悬臂梁模型基本参数为:长度l=1m，矩形截面尺寸0.05m×0.05m，材料为F141钢，弹性模量E=190GPa，密度ρ=8000kg/m3；天平位置xB=0.8×l；设置一个加速度计，位置xA=0.7×l，每间隔Ts=0.0001s记录一次气动力和加速度数据，即采集频率Fs=10000Hz；质量比系数为η=0.5，在集中质量上施加单位冲量作为脉冲载荷，使其获得初速度v=0.1m/s。

本文用小波分析方法处理振动信号，其具有时域和频域同时局部化和多尺度分辨的功能，非常适合非平稳信号的处理。设信号占据最高频率空间V0，对于一个正交多分辨率分析，有…Vj+1⊂Vj…V1⊂V0，可知Vj+1是Vj的真子空间，则:

Vj=Vj+1⊕Wj+1

(14)

其中，Wj+1为Vj+1的正交补空间。Vj+1也称为Vj的低频子空间，表现了Vj对应频带的低频部分，为近似信号；Wj+1称为Vj的高频子空间，表现了Vj对应频带的高频部分，为细节信号。显然这种分解可以持续进行，有:

V0=W1⊕W2…⊕WJ⊕VJ,J∈N

(15)

上式表明原始信号可用一系列的细节信号和近似信号叠加而成，同时表明分解结果可以保证信号的完全重构。由此可以将加速度信号(以A表示)进行J层小波分解为:

(16)

式中,AaJ为第J层近似信号，Adj为第j层细节信号。

3.2 结果分析

由上述悬臂梁模型基本参数进行理论分析，可以算出各阶振型对应的λi和ωi，代入式(13)，可得多阶惯性补偿系数，如表1所示。

表1 多阶惯性补偿系数Table 1 Multi-order inertial compensation coefficients

图4为悬臂梁冲激响应的加速度信号，可以看出：在初始时刻，加速度信号有较大范围的波动(因为初始时刻超高频分量没有完全衰减)；此后，加速度信号迅速趋于平稳震荡。由于初始时刻非常短暂，并不会对气动力补偿结果造成较大的影响。

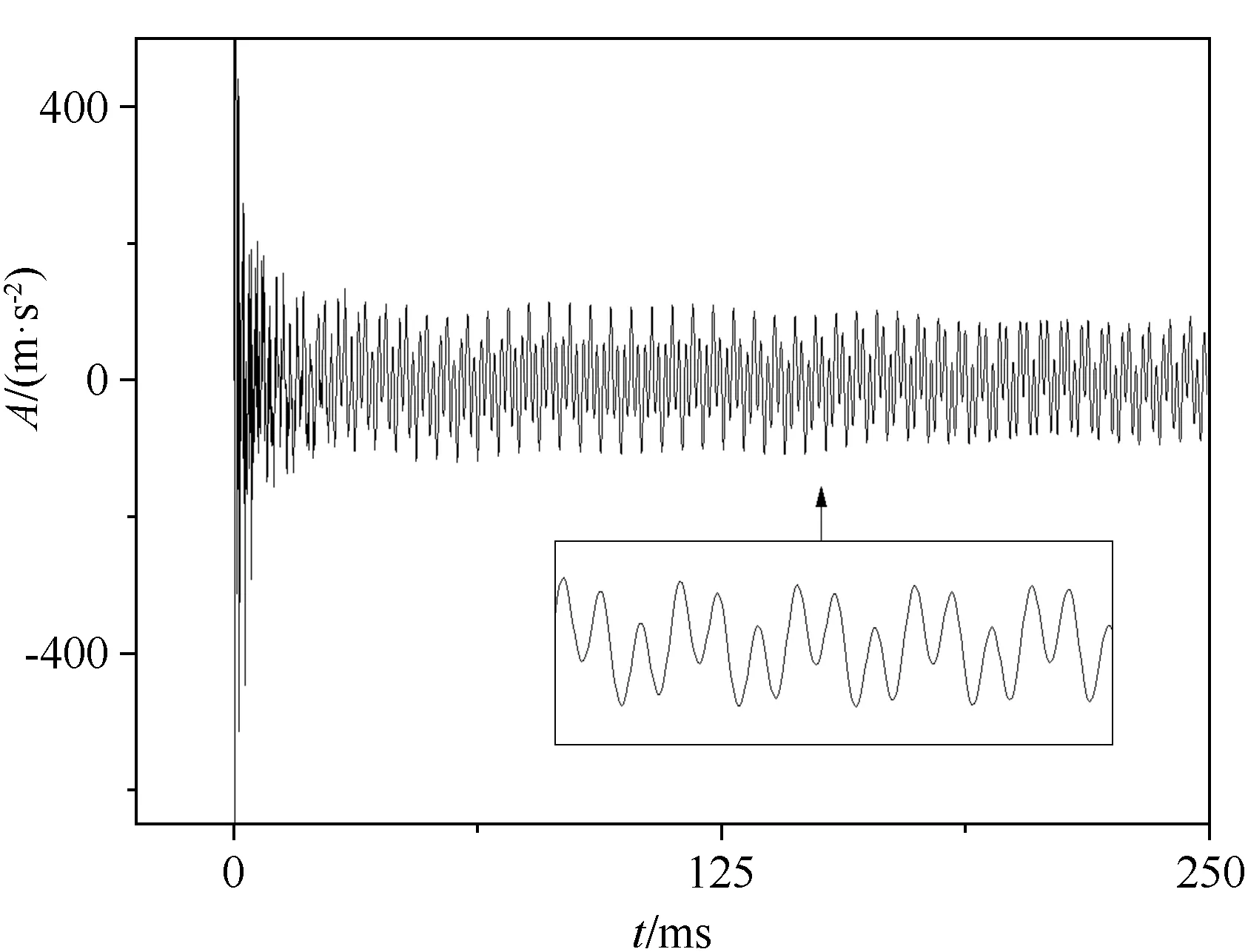
图4 冲激响应加速度信号

对“采集”到的天平和加速度信号进行频谱分析，如图5所示，可见天平和加速度信号的能量主要集中在前3阶频率，因此对悬臂梁前3阶惯性力补偿即可达到比较理想的效果。

根据加速度信号的前3阶固有频率分布情况(采集频率Fs=10000Hz)，采用“dmey”小波进行6尺度变换与重构。根据离散小波子空间频域划分方法，加速度信号第1阶、第2阶和第3阶固有频率分别落在第6层近似信号、第5层细节信号和第4层细节信号对应的频域，因此经过小波分解后，前3阶加速度信号可以相互分离，如图6所示。

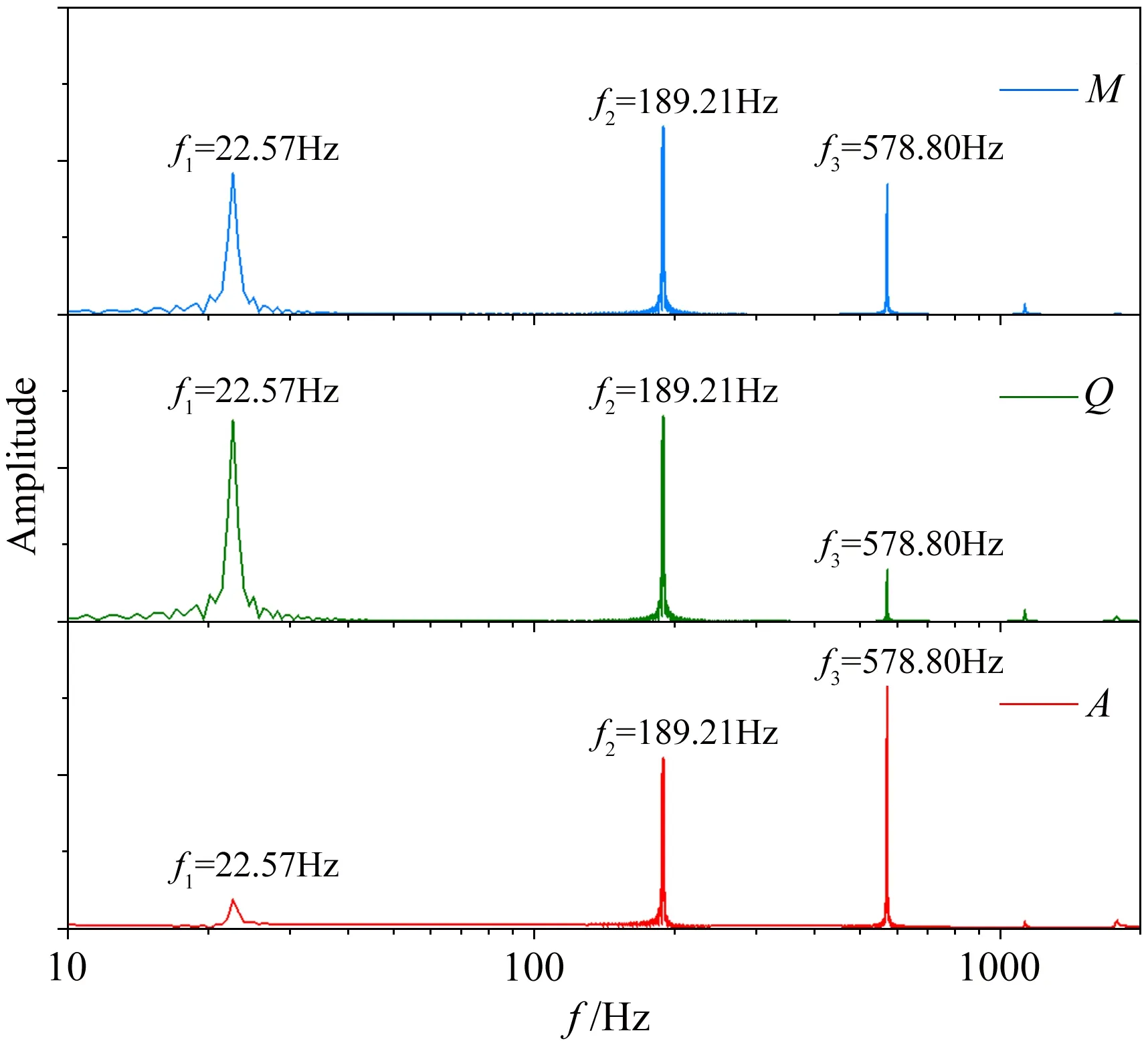
图5 天平和加速度信号频谱分析

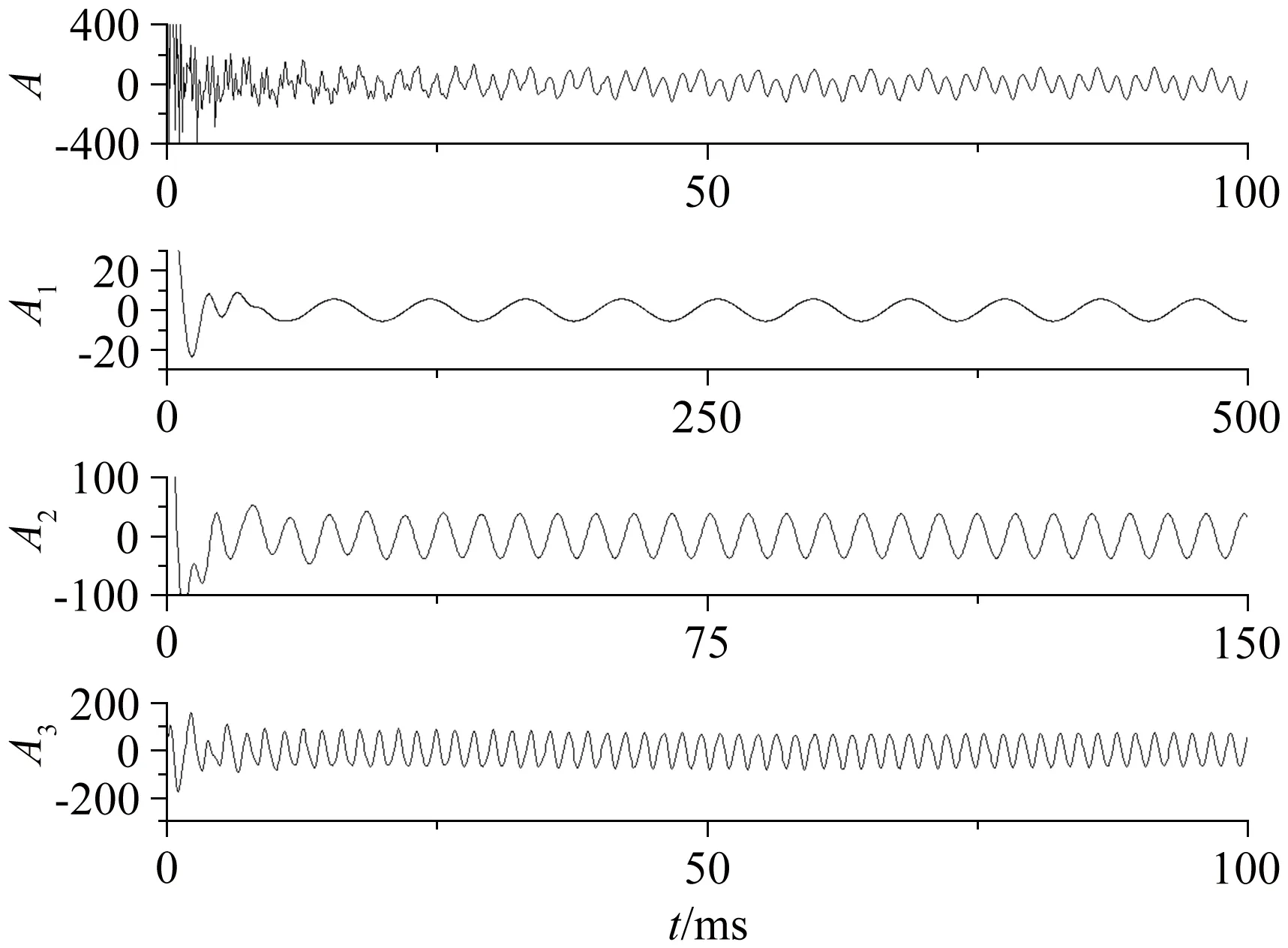
图6 加速度信号小波分解

将加速度模态分解结果和表1中的补偿系数代入式(11)中，得到气动力的多阶惯性补偿结果；而将天平和加速度信号代入式(9)中，利用最小二乘法拟合公式(9)，得到传统方法的补偿系数；反过来将补偿系数和加速度信号代入式(9)中，可得到传统方法补偿结果，如图7所示。图7中M和Q表示天平原始数据，MT和QT表示传统方法补偿结果，MC和QC表示多阶惯性补偿结果。

可以看出：(1) 相比传统补偿方法，多阶惯性补偿方法进一步降低了天平震荡的幅值，缩短了天平的稳态时间，提高了天平的响应速度。(2) 采用单个加速度计的传统补偿方法只能补偿或部分补偿气动力的单一频率分量，而多阶补偿方法对气动力的前3阶频率分量都能补偿;如果进一步提高多阶惯性补偿的阶数，可以使其补偿精度更高。(3) 采用理论补偿系数进行多阶惯性补偿，良好的补偿效果验证了理论分析的正确性。

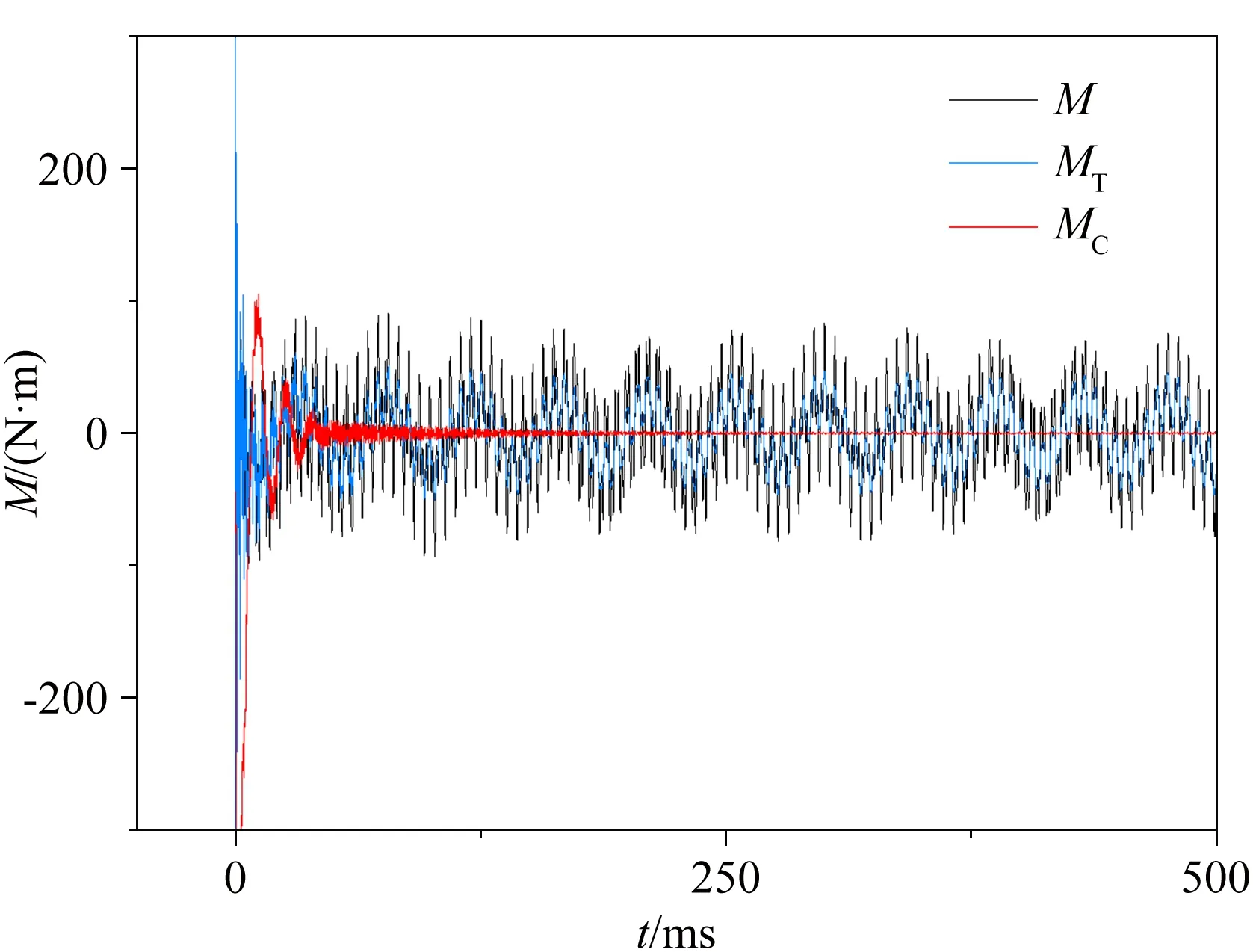
(a) 俯仰力矩

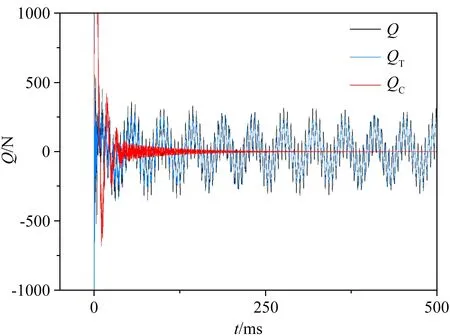
(b) 法向力

4 结 论

本文应用振动力学理论对测力系统简化模型自由振动特性进行了研究，根据不同振型振动干扰与加速度分布规律不一致的特点，提出了多阶惯性补偿方法。多阶惯性补偿方法解决了传统方法对天平信号多频振动干扰补偿精度不高的问题，进一步提高了天平的动态特性。在后续工作中，应进一步研究测力系统受强迫载荷下的振动特性以及补偿方法；如果使用多个加速度计进行动态补偿，如何应用多阶惯性补偿方法以及如何布置加速度计的相对位置,可作为下一步研究重点。