基于γ-Reθ转捩模型的高超声速 复杂构型转捩模拟
2018-11-15易淼荣赵慧勇乐嘉陵
易淼荣, 赵慧勇, 乐嘉陵
(中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室, 四川 绵阳 621000)
0 引 言
边界层转捩现象对航空领域中的摩阻和热流具有重要影响。对于高超声速吸气式飞行器来说,若流入进气道的边界层为层流,则有可能因逆压梯度和激波边界层干扰而引起流动分离,但湍流边界层在抵抗分离方面具有优势。因此,为了提高飞行稳定性,同时增加燃烧室内燃料和氧气的混合,经常会在进气道前体上安装强制转捩装置,以促进边界层在进入唇口之前转捩为湍流。然而,尽管对边界层转捩现象的研究已经长达一个多世纪,人们仍然不能确切地给出什么情况下边界层会由层流转捩成为湍流,特别是在高超声速复杂构型下,由于受到太多因素(湍流度、雷诺数、马赫数、粗糙度、钝度、壁温、几何构型等)及各种因素之间互相耦合作用的影响,使得转捩预测更加困难。
现阶段,有多种数值方法可以用来进行边界层转捩研究。DNS和LES被用来研究典型状态下的基本转捩机制和详细的转捩过程[1-2];LST和PSE 则被用来研究非稳定波的形成和发展历程;转捩准则则在总结大量实验数据的基础上,用简单的形式给出转捩位置[3-4],如NASP的尖前缘平板转捩准则:Reθ/Mae=305[5]。目前来看,半经验的eN方法在工程上的应用最为广泛,但是eN方法也有几个致命缺陷:由于其基于线性稳定性理论,故难以处理较为复杂的构型,更无法模拟粗糙颗粒诱导的转捩;同时N因子的确定也需要大量的试验数据,而且其在不同马赫数、不同构型下的具体数值也不一样;而且,来流湍流度本是影响转捩的一个重要因素,但在eN方法中却没有任何体现。相反,基于RANS模型发展而来的工程转捩模型,则因其具有较好的鲁棒性且易于与现有的湍流模型框架融合而在最近越来越得到人们的重视,其中,Langtry和Menter[6-8]基于SST湍流模型,提出了一种基于经验耦合的间歇因子转捩模型——γ-Reθ模型。在该模型中,所有的计算都是基于局部变量,没有任何沿流线积分的操作,因此可以轻易地对复杂构型进行模拟,Langtry将该模型应用于大量低速工程算例。由于γ-Reθ转捩模型只是为把基于经验关系式的模型结合进一般CFD方法中提供了一个框架,而具体的物理机制均包含在经验关系式中,因此很多研究者在其框架下针对各种不稳定机制对模型进行修正,从而适应不同情况下的转捩模拟。如Watanabe[9]通过类比Görtler不稳定性和横流不稳定性,引入类似于Görtler数的Kohama参数,Krumbein[10-11]针对三维边界层,通过求解Falkner-Skan-Cooke近似解引入横流转捩动量厚度雷诺数,各自提出了基于该框架下能够模拟横流模态的转捩模型。Langel[12]则通过引入“粗糙幅度” 的输运方程发展了能够反映壁面粗糙度影响的修正版本。在高超声速领域,Krause[13]和Zhang[14]分别提出了可以应用于高超声速情况下转捩预测的经验关系式及相应的修正,并都将其应用于Ma8.3的双楔平板模型,得到了与试验吻合较好的壁面压力分布。Cheng[15]则添加了一个针对压力梯度的修正因子,对Ma7.93的7°尖锥进行了模拟,研究了来流湍流度和网格对计算结果的影响。Bensassi[16]模拟了Ma8的7°尖锥模型,得到了与试验一致的壁面热流分布。但是,目前并没有见到该模型在更复杂构型上的应用,如光滑壁面或安装有转捩带的高超声速进气道构型。
本文基于Langtry和Menter的γ-Reθ模型,进行一些必要的修正,建立一套适用于高超声速情况下的转捩预测方法。通过较为简单的三维构型自然转捩和粗糙颗粒诱导强制转捩的算例对模型进行了验证。将修正的模型应用于X-51A前体边界层自然转捩和强制转捩的研究中,通过与试验结果进行比较,表明本文建立的方法能够较好地进行高超声速复杂构型中的自然转捩和强制转捩预测。
1 数值计算方法
1.1 流场求解器
本文的γ-Reθ模型是基于一套有限体积大规模并行结构网格Navier-Stokes求解器AHL3D建立的。该求解器由中国空气动力研究与发展中心吸气式高超声速技术研究中心开发,能够对理想气体和化学非平衡状态下的混合气体进行求解[17-18]。时间积分采用 LU-SGS,无粘通量采用重构-推进方法,重构采用 3 阶MUSCL插值,推进采用Steger-Warming和AUSMPW+格式,粘性通量采用改进的Gauss定理计算。湍流模型为Menter的SST双方程模型。
1.2 γ-Reθ转捩模型
Langtry和Menter[6]提出的γ-Reθ转捩模型主要基于间歇因子γ和转捩起始动量厚度雷诺数Reθt的输运方程。γ方程用来控制转捩程序,其源项由临界动量厚度雷诺数Reθc和最大涡雷诺数Rev之间的关系来控制,而Reθc又与Reθt存在对应关系。Reθt则被当做一个输运标量,主要思想就是使用经验耦合关系式得到边界层外的Reθt,并且允许Reθt通过输运方程扩散到边界层内去。具体形式如下:
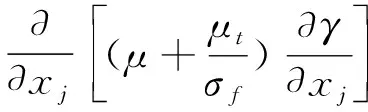
(1)
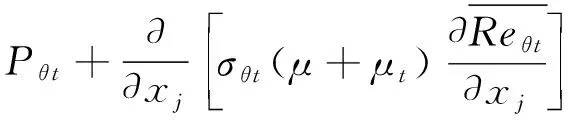
(2)
Pγ=Flengthca1ρS[γFonset]0.5(1-ce1γ)
(3)
Eγ=ca2ρΩγFturb(ce2γ-1)
(4)
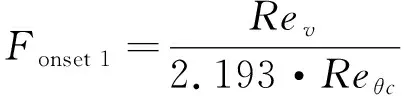
(5)
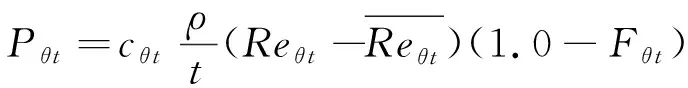
(6)
Reθ t=F(Tu)F(λθ)
(7)

(8)
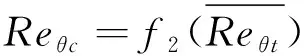
(9)

(10)
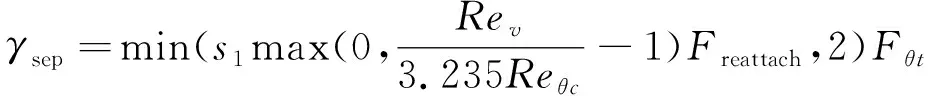
(11)
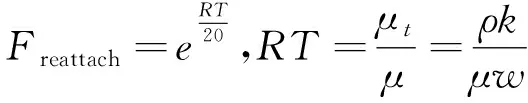
(12)
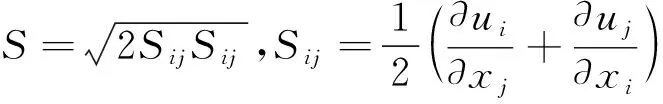
1.3 针对模型的修正
原始的转捩模型是针对低速情况提出的,因此不能直接应用于高超声速情况下的转捩预测,这个模型一经提出,很多研究者均在其框架下针对各种情况对模型的Reθc和Flength进行修正,前者用来修正转捩起始位置,后者用来修正转捩区域长度。如Krause和张晓东均提出了该框架下能够应用于高超声速情况下的经验关系式。Krause[13]的修正如下:
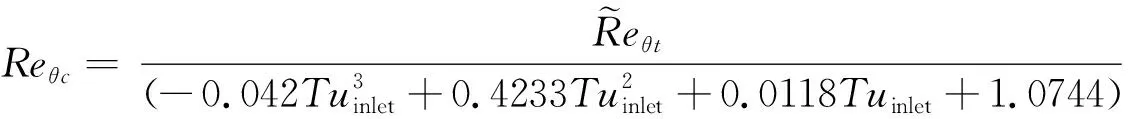
(13)
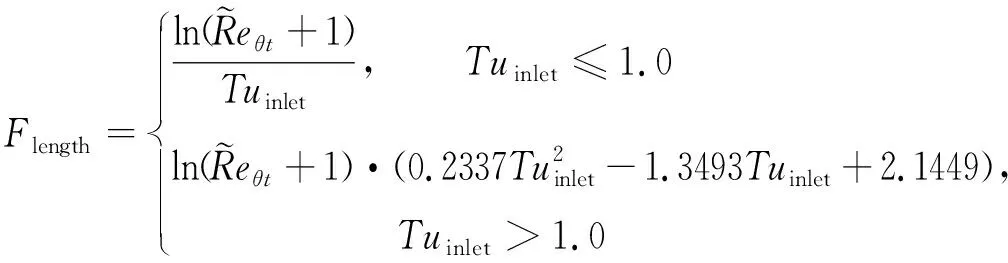
(14)
将来流粘性比RT∞设置成0.001,因此Tu在到达模型前缘时均衰减到了一个很小的值,通过将Tuinlet加入到经验关系式中来体现不同来流湍流度对转捩的影响规律,经过系列低速平板的标定后,应用于Ma8.3下双楔模型试验的转捩预测中,得到的壁面压力系数与试验吻合较好,显示出高超声速情况下预测转捩的潜力。尚庆[19]也采用该修正关系式对双楔模型进行了更进一步的研究,其结果显示基于该修正关系式的γ-Reθ转捩模型能够在压力系数、热流Stanton数和分离区大小上与试验吻合良好。
张晓东[14]的修正则如下所示:
张晓东还基于Reshotko[20]对高超声速试验中Reθ t与边界层外缘马赫数Mae关系的总结,利用当地马赫数对模型进行了马赫数修正,以适应不同Ma数下的转捩预测情况:
Ma∈[0,12]
(17)
张晓东也对双楔模型进行了与试验吻合较好的模拟。
本文利用文献[21]中的进气道构型,采用二维计算对转捩模型进行考核及修正。进气道外压缩形式为四波系平面顶压,流道全长为550mm,本文模拟其唇口之前压缩面的情况,模型构型及网格如图1所示。来流条件如表1所示,表中case3模拟的是在距前缘88mm的第一道压缩面上安装了高度为1mm的钻石型转捩装置的试验结果,转捩带的具体参数可参考文献[22],由于是二维模拟,转捩带构型模化为矩形。计算时为了更好地与试验对比热流值,壁面温度根据实验测量结果分段给定。对比用到的试验数据来自于文献[21-22]。

图1 高超声速进气道二维模型及网格示意图
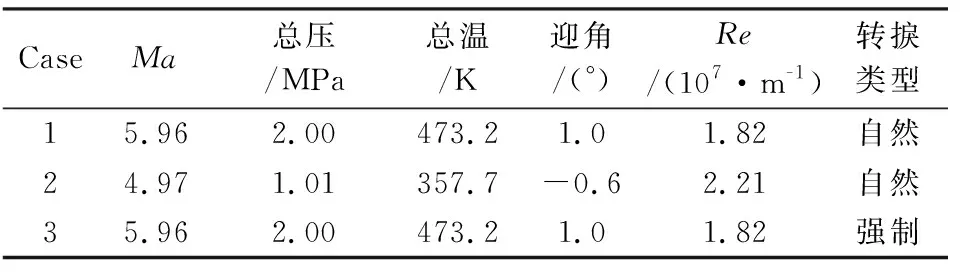
CaseMa总压/MPa总温/K迎角/(°)Re/(107·m-1)转捩类型15.962.00473.21.01.82自然24.971.01357.7-0.62.21自然35.962.00473.21.01.82强制
试验在FL-31风洞中进行。FL-31属于常规噪声风洞,根据一般的认识,常规噪声风洞的来流湍流度约为1%的量级。在case1情况下,Menter、Krause及张晓东三种版本的经验关系式在不同来流湍流度下的计算结果与试验结果比较如图2所示。从图中可以看出,Menter版本和Krause版本在来流Tu=0.03时(图中Tu0.03表示来流湍流度为0.03%,RT1表示来流湍流粘性比μt/μ为1),转捩位置仍早于试验值,明显过早地预测了转捩的出现。因此,在本程序框架下,Menter版本和Krause版本将无法正确模拟FL-31风洞湍流度水平下的转捩,更无法模拟静音风洞或飞行试验条件等低湍流度情况下的转捩,而张晓东版本则能在本程序框架下正确反映FL-31风洞的来流湍流度的量级,因此选取张晓东提出的经验关系式作为本文采用的版本。
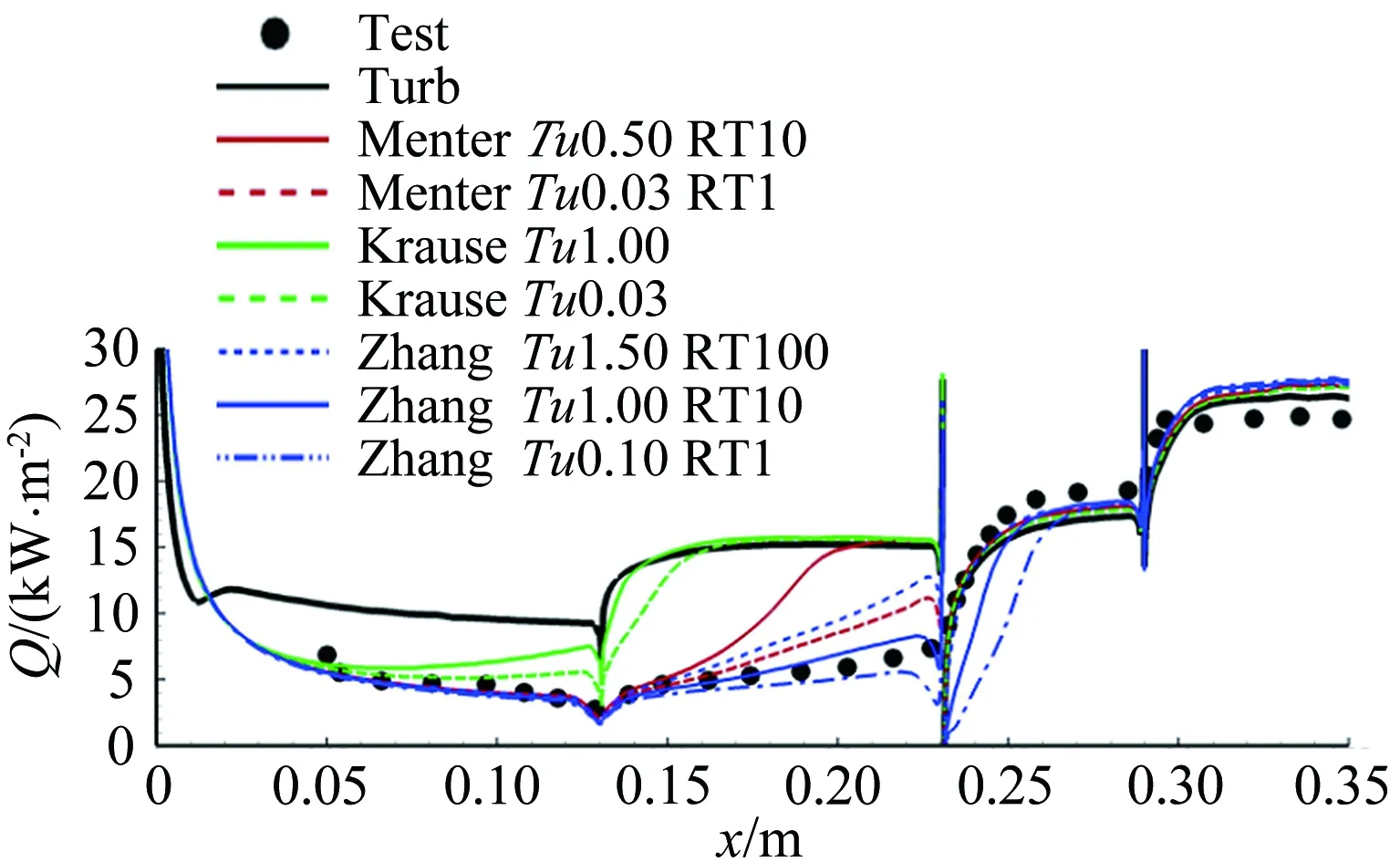
图2 不同计算方法得到的热流分布(case1)
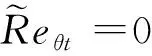
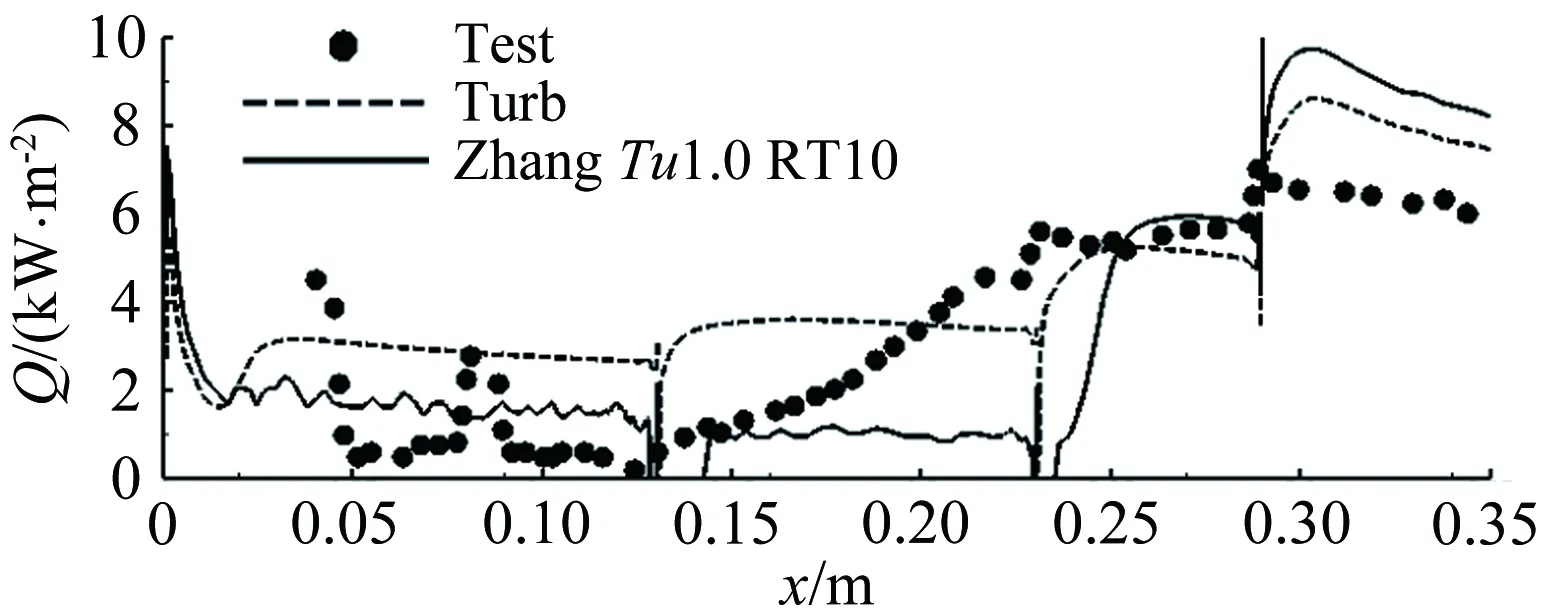
图3 自然转捩热流分布(case2)

图4 强制转捩热流分布(case3)
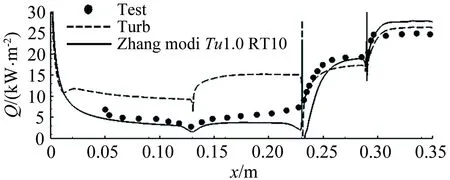
图5 自然转捩热流分布(case1,修正后的模型)
Fig.5Heatfluxdistributionofnaturaltransition(case1,modifiedmodel)
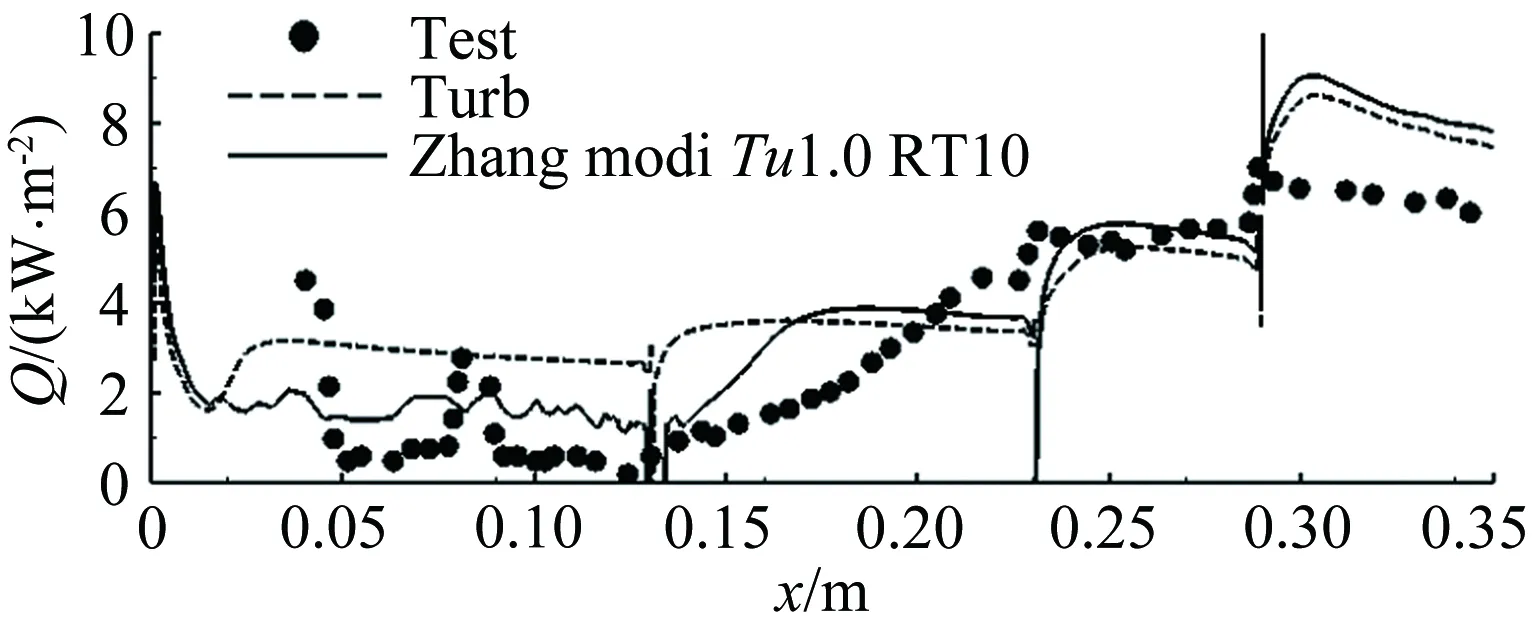
图6 自然转捩热流分布(case2,修正后的模型)
Fig.6Heatfluxdistributionofnaturaltransition(case2,modifiedmodel)
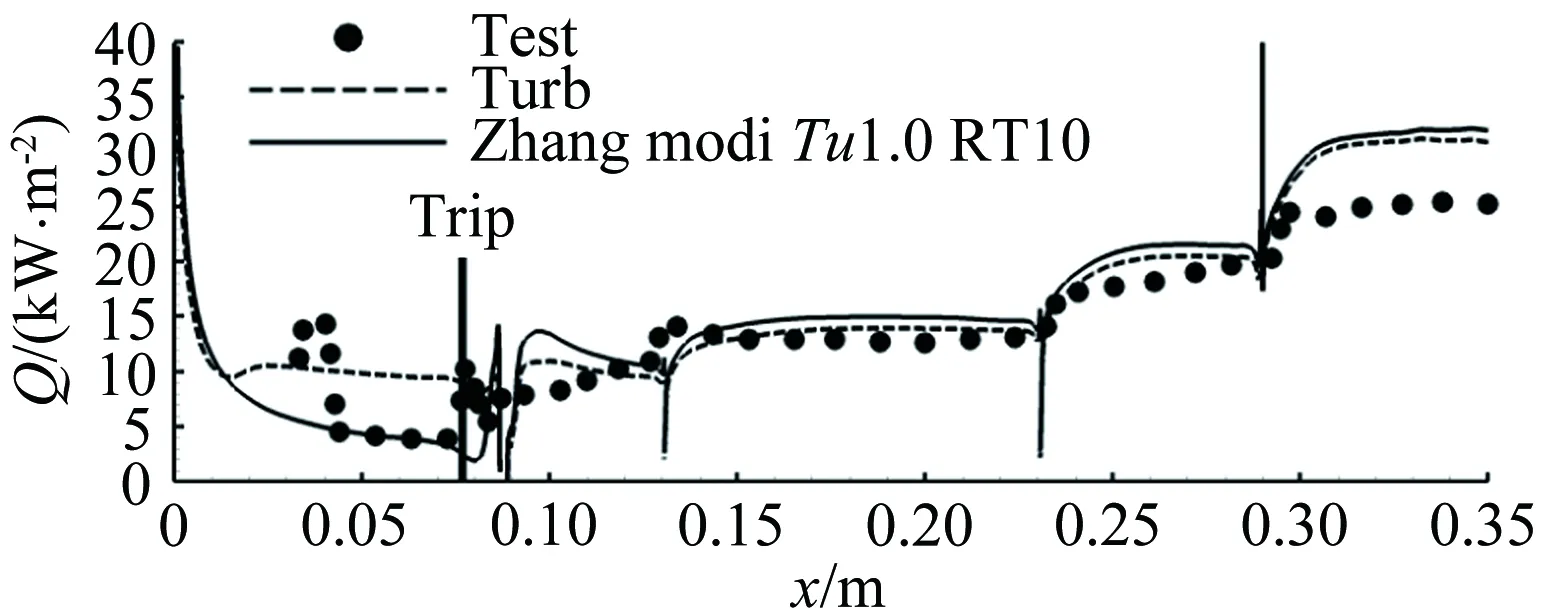
图7 强制转捩热流分布(case3,修正后的模型)
Fig.7Heatfluxdistributionofforcedtransition(case3,modifiedmodel)
修改后的k-w方程为:
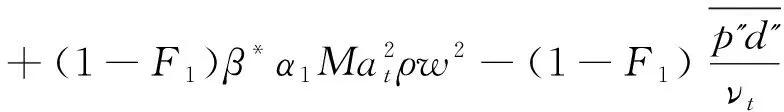
(18)
其中:
α1=1.0,α2=0.4,α3=0.2
两个经验关系式为:
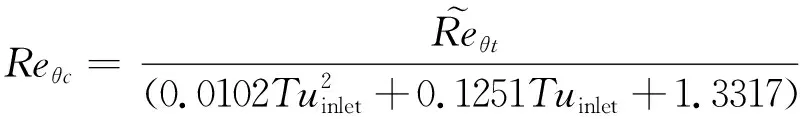
(19)
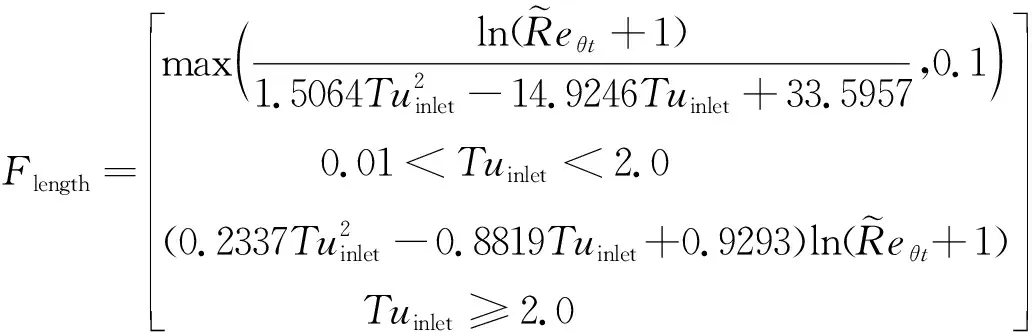
(20)
此外,对Reθ t的修正改为:
Ma∈[0,12]
(21)
1.4 网格无关性验证
将修正后的转捩模式在1.3节中的二维构型中进行网格无关性验证。选取1.3节中的case2,并以1.3节中的网格为base网格,网格在第一至第四道压缩面的流向上分别布置了121、61、41、65个网格点,在法向上布置了141个网格点,第一层网格距离壁面0.001mm。总的网格量约为6万。再在此基础上在法向加密1.5倍得到v1.5网格,在法向和流向各加密1.5倍得到v1.5-s1.5网格。3套网格的计算结果如图2所示。从中可以看出,3套网格计算得到的热流几乎重合,可认为转捩模型此时已经达到网格无关性。
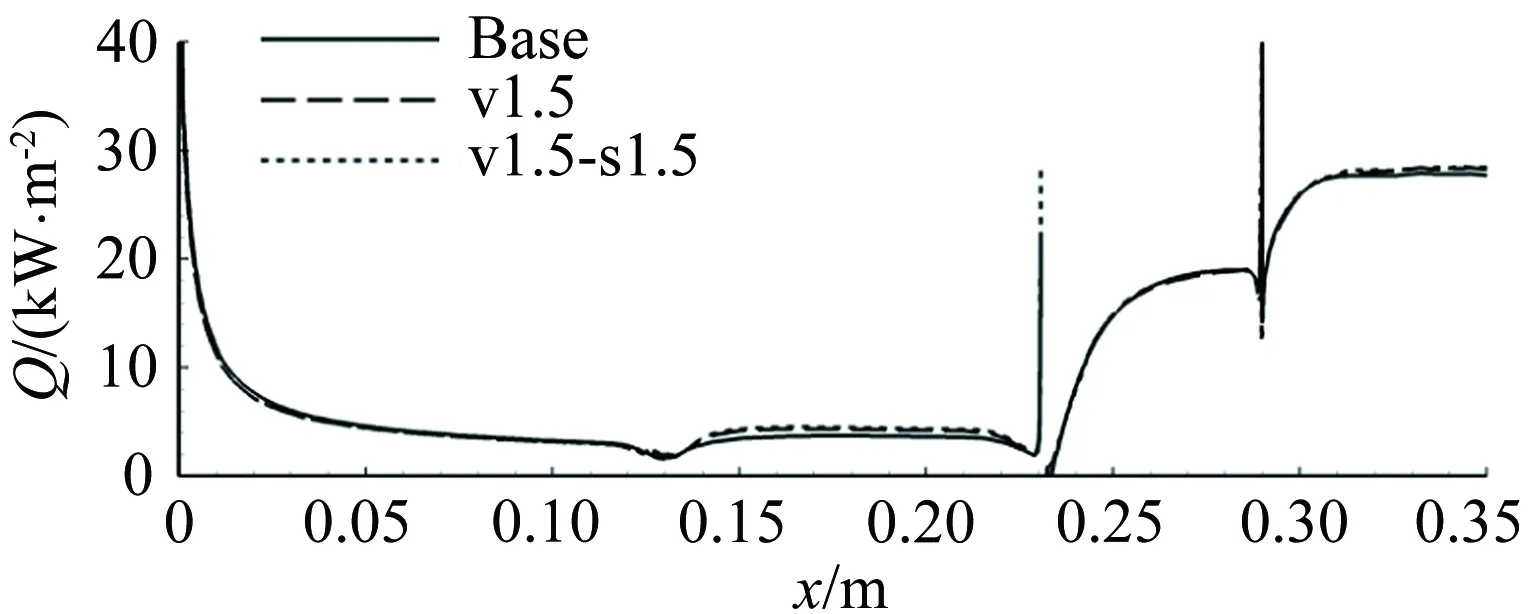
图8 多套网格计算结果(case2,修正后的模型)
2 计算结果与分析
由于上一节对模型进行的修正都是以二维计算为基础,为了验证其是否能够适应更宽的马赫数、雷诺数范围及三维复杂构型的转捩预测,选取了Ames的全尺寸升力体构型在有迎角情况下的转捩,验证模型对高超声速三维构型自然转捩的预测能力;通过Ma6平板上单个粗糙颗粒诱导转捩的算例,验证模型对粗糙颗粒诱导强制转捩的预测能力。最终,将模型应用于X-51A进气道构型的转捩模拟当中。
2.1 Ma7.4 下 Ames 的 all-body 试验
Lockman[24]对Ames研究中心的all-body三维升力体提供了一个完整的高超声速三维实验,模型是一个用于高超声速巡航的通用升力体外形。实验是在Ames的3.5英寸高超声速风洞开展的。模型示意图见图9。模型全长0.9144m,具有75°后掠角的尖三角翼形状。全体是一个主轴比4的椭圆锥,后体的横截面是具有直边的椭圆形。实验条件如表2所示。网格拓扑如图10所示,保持壁面第一层y+<1,网格量约为150万。来流湍流度设为 0.5%。

表2 全尺寸升力体模型风洞试验来流条件Table 2 Test conditions for the all-body model
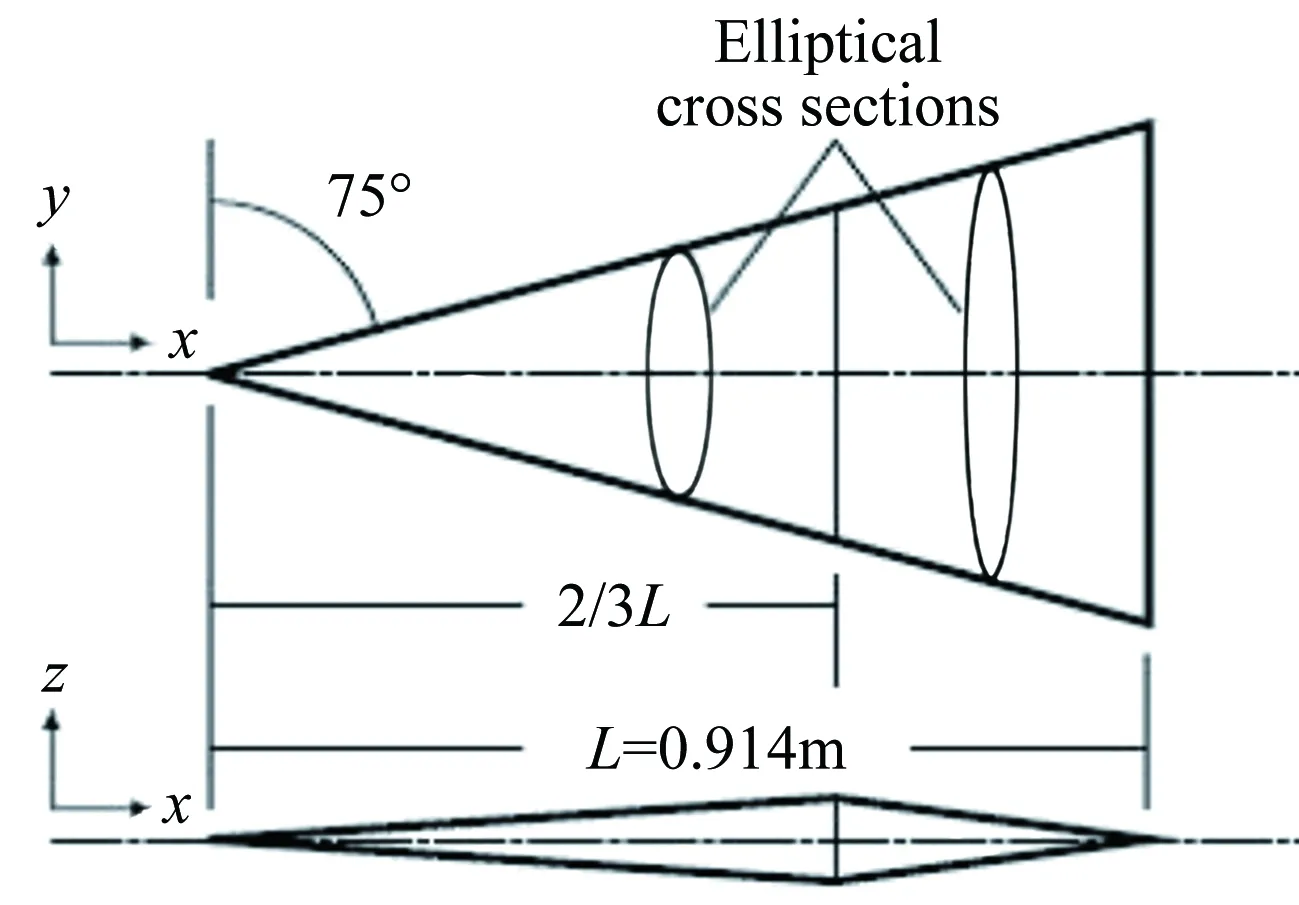
图9 全尺寸升力体模型示意图
图10 全尺寸升力体模型网格示意图
试验测量了迎风面和背风面表征热流的Stanton数,即St,其定义为:
ρ∞和U∞分别表示来流密度和速度,Hw为壁面上流体的焓值,Ht表示来流总焓。
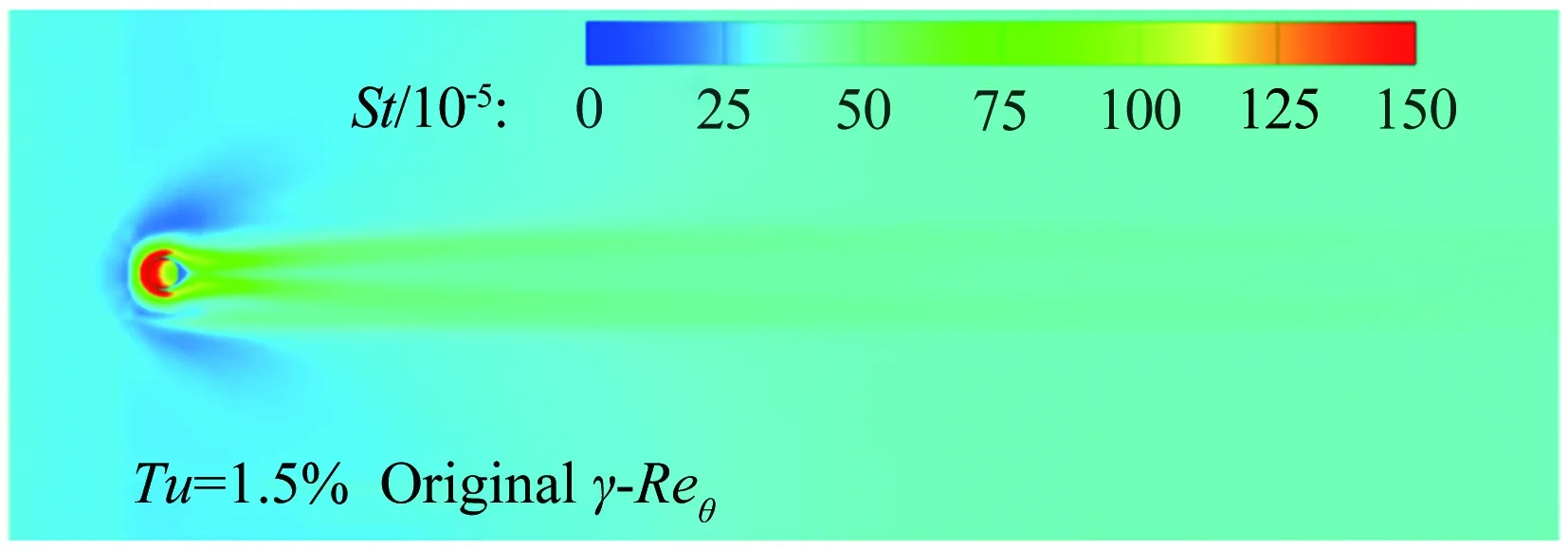
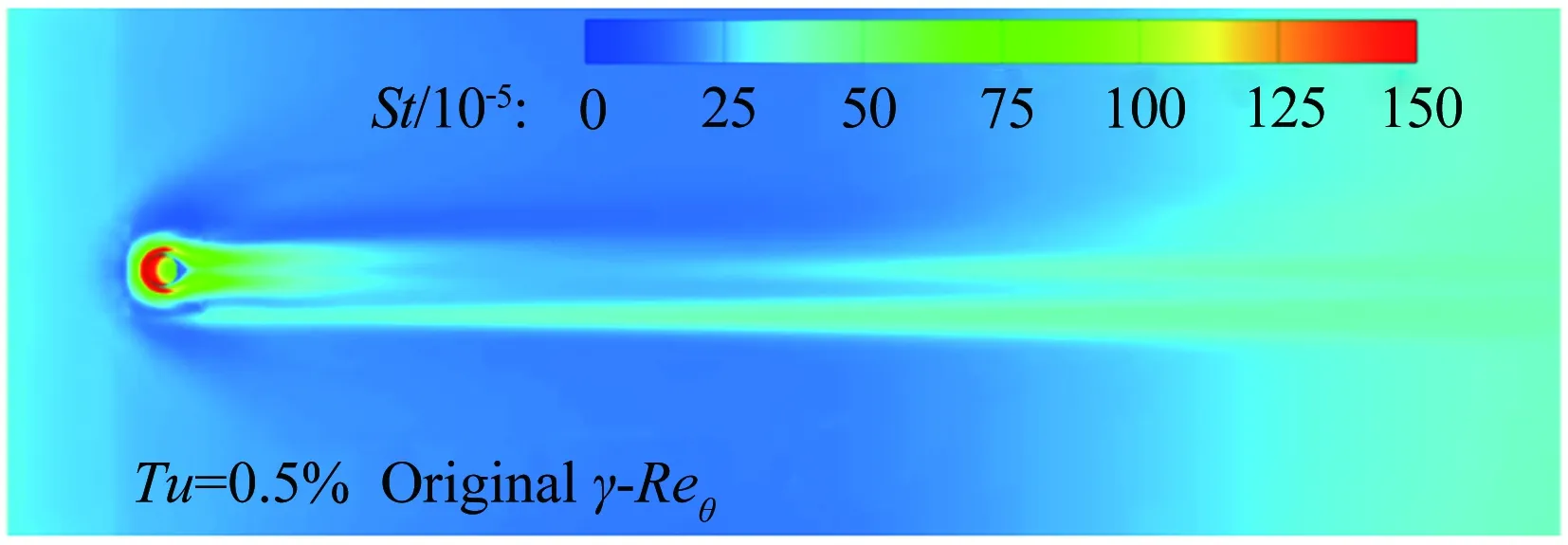
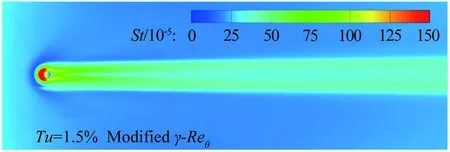
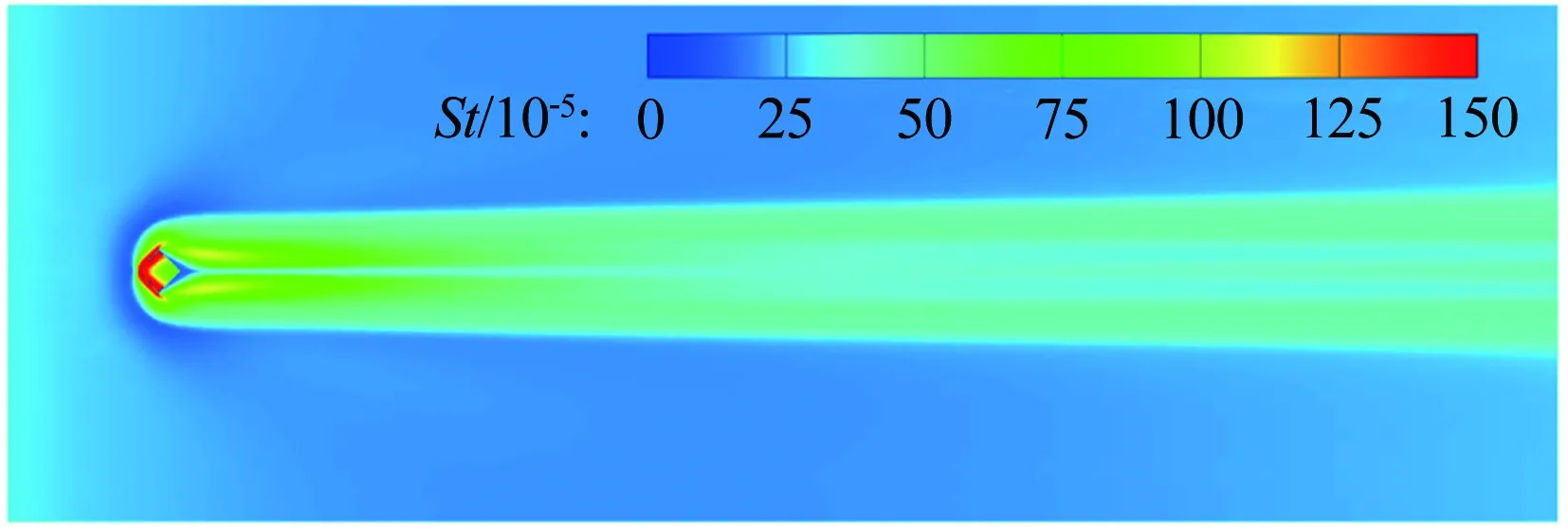
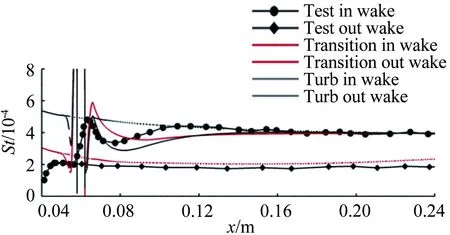
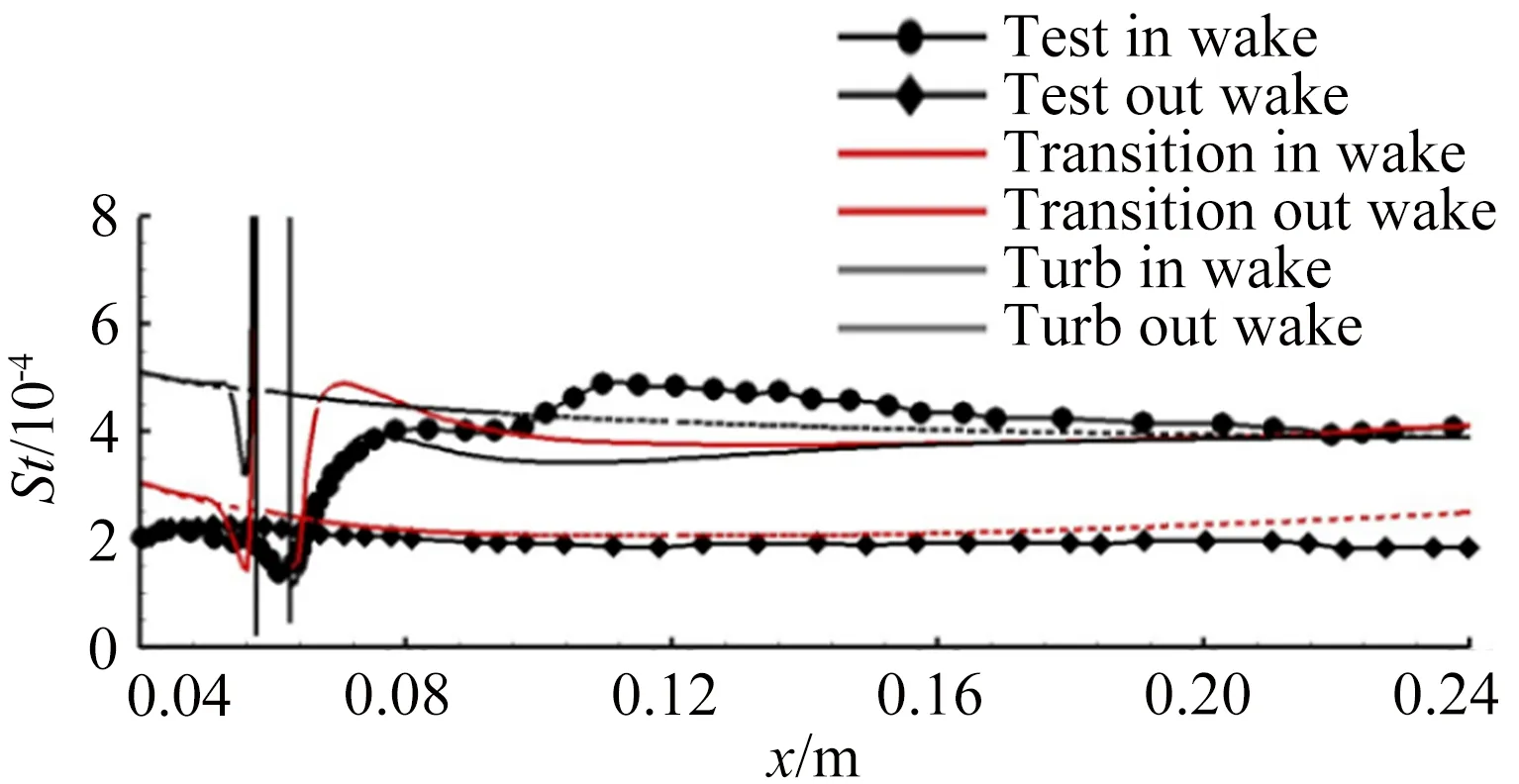
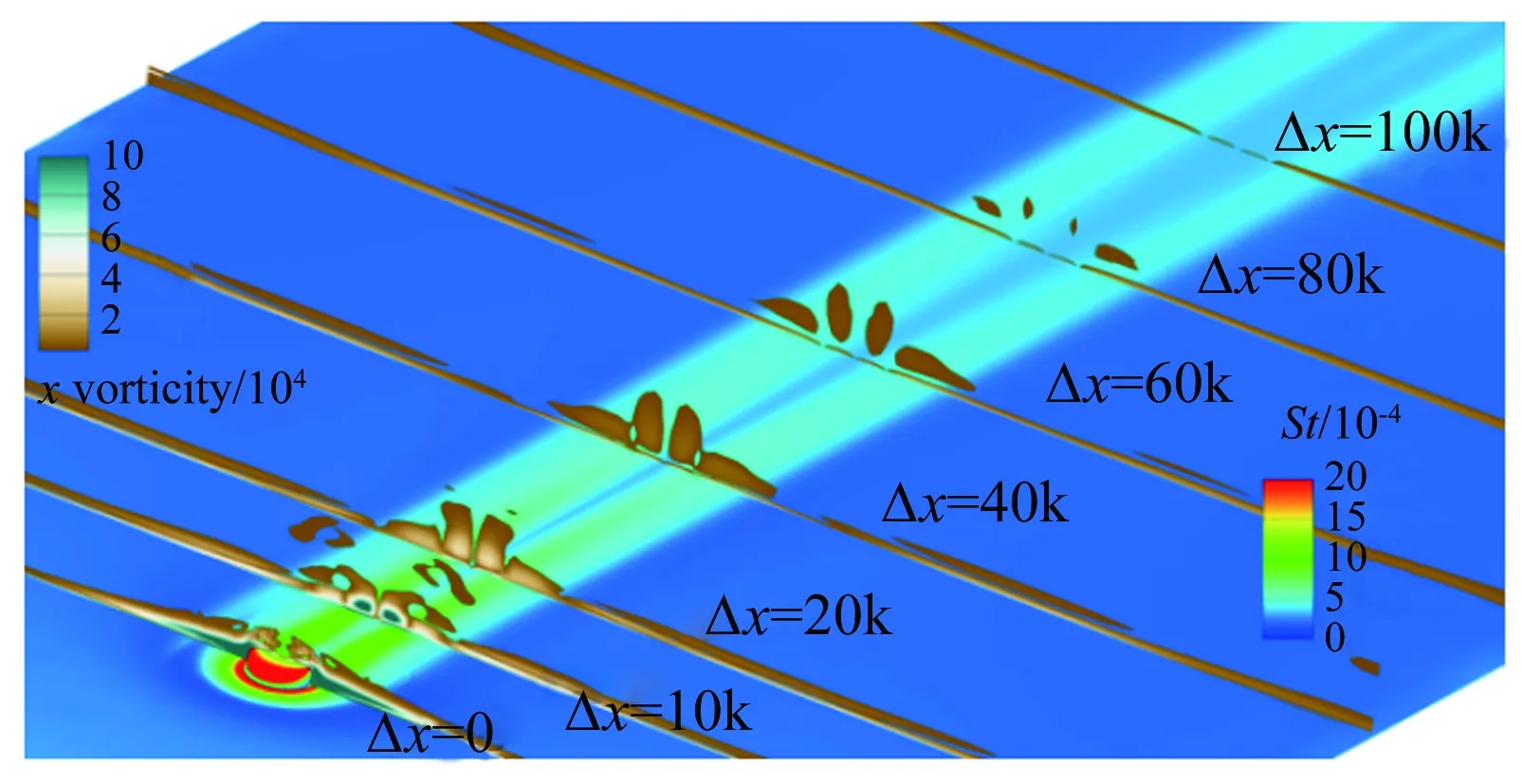
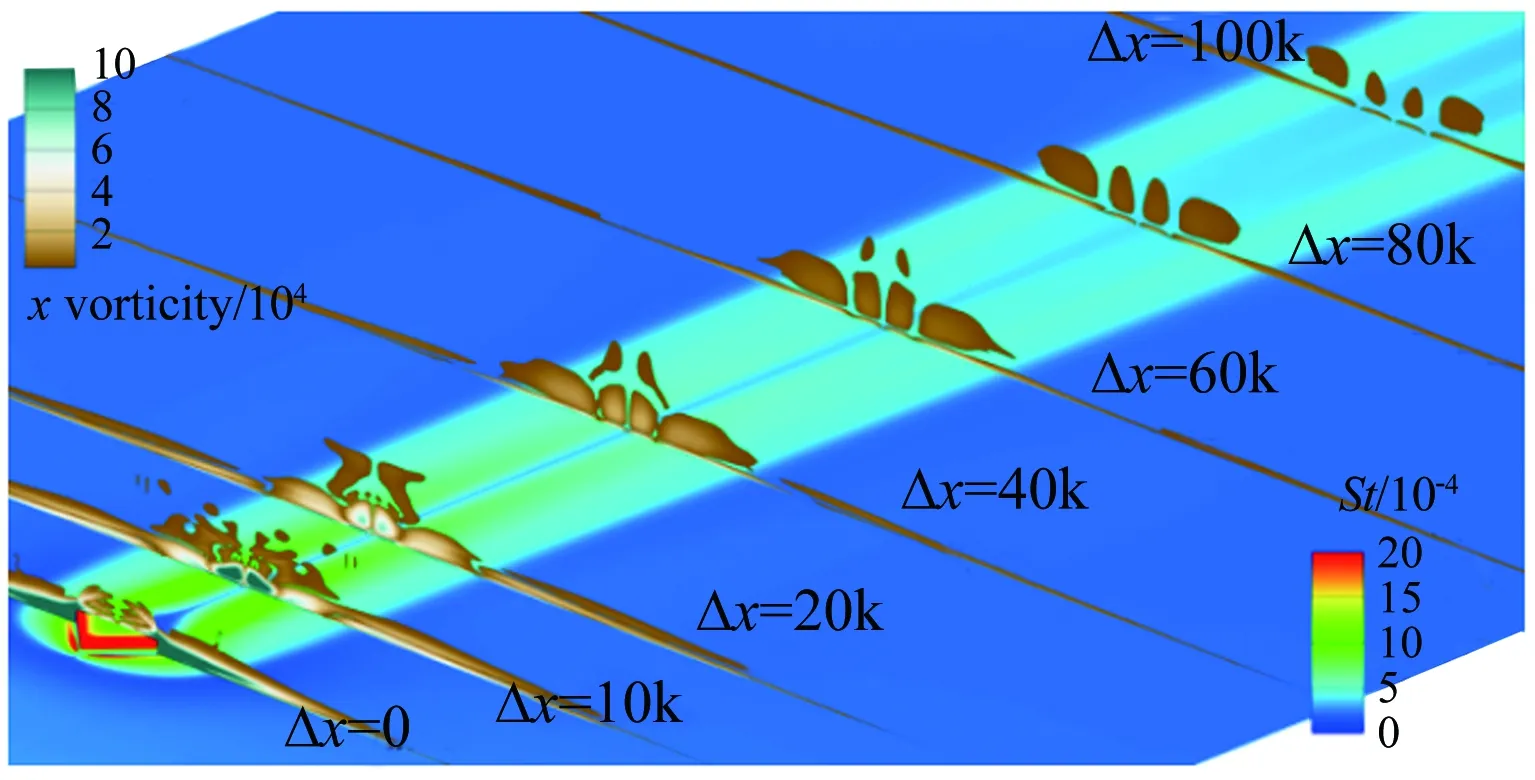
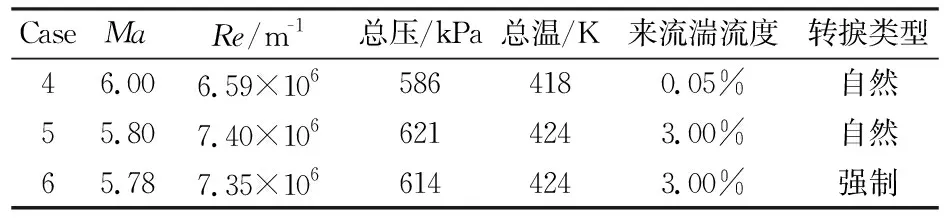
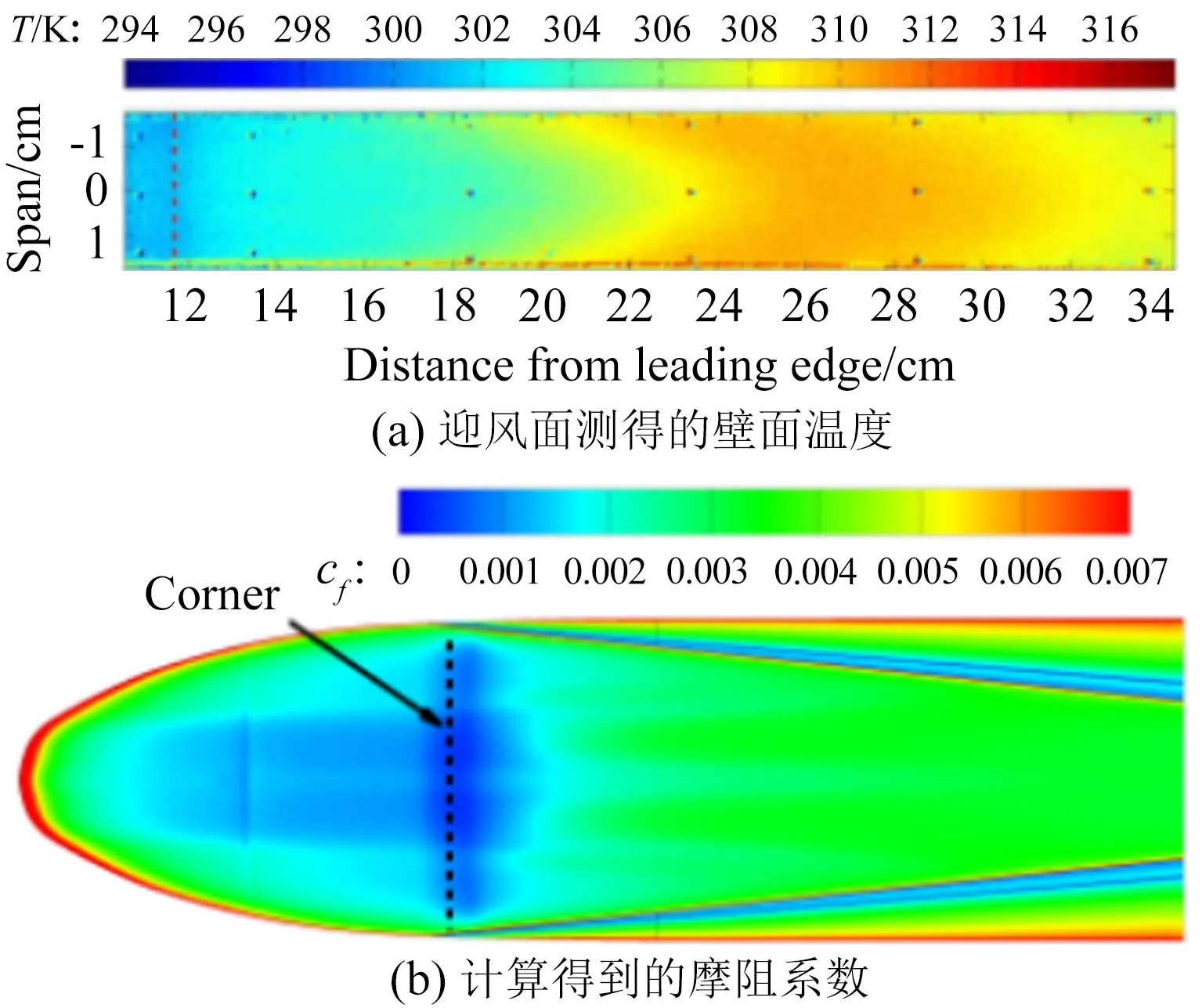
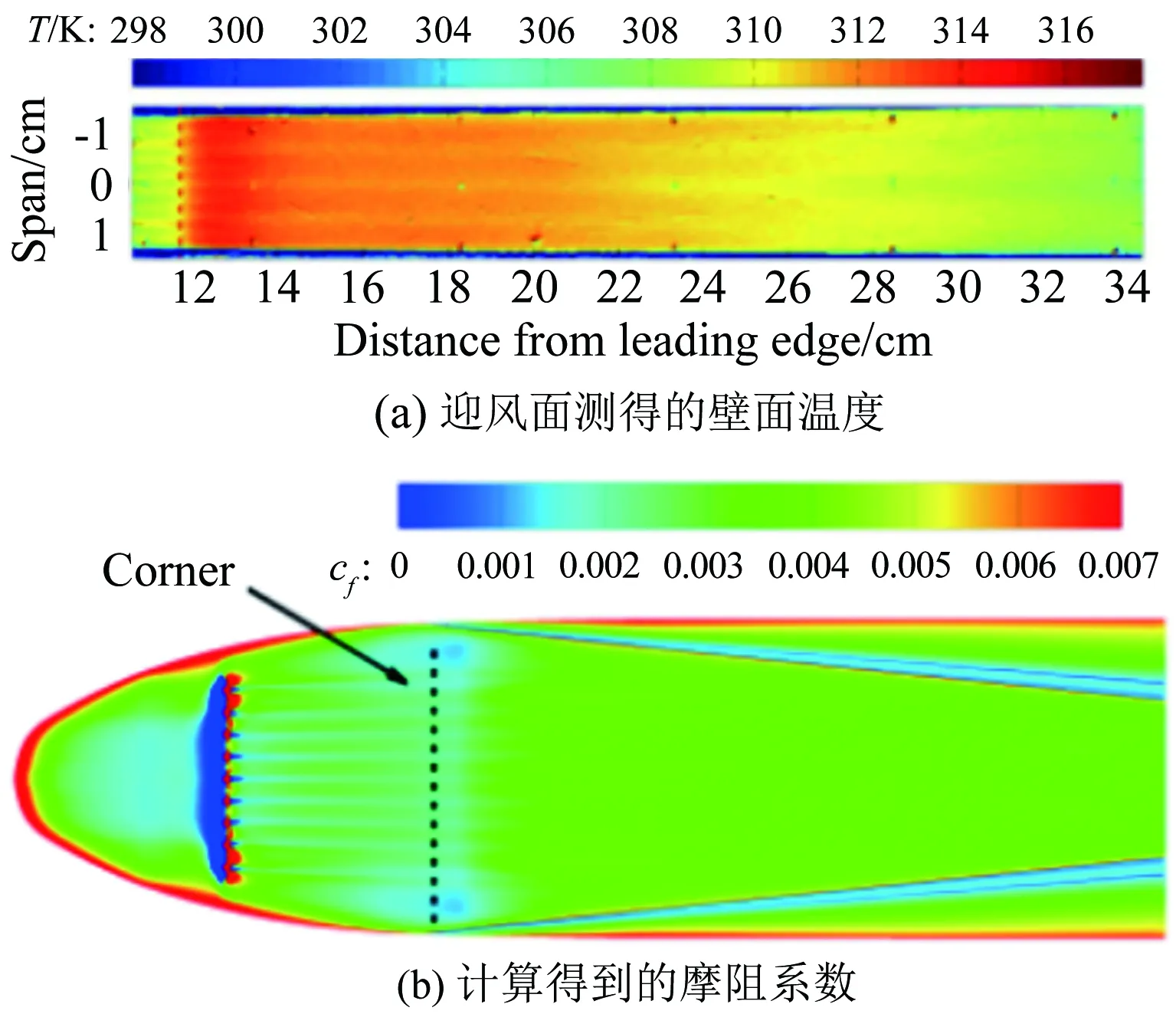
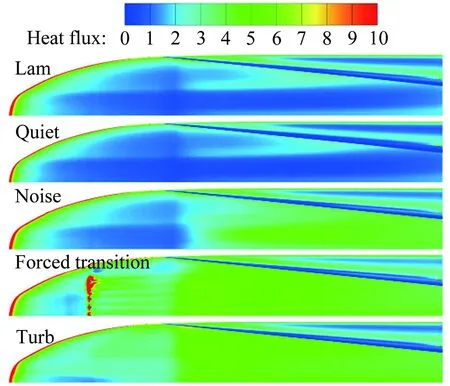
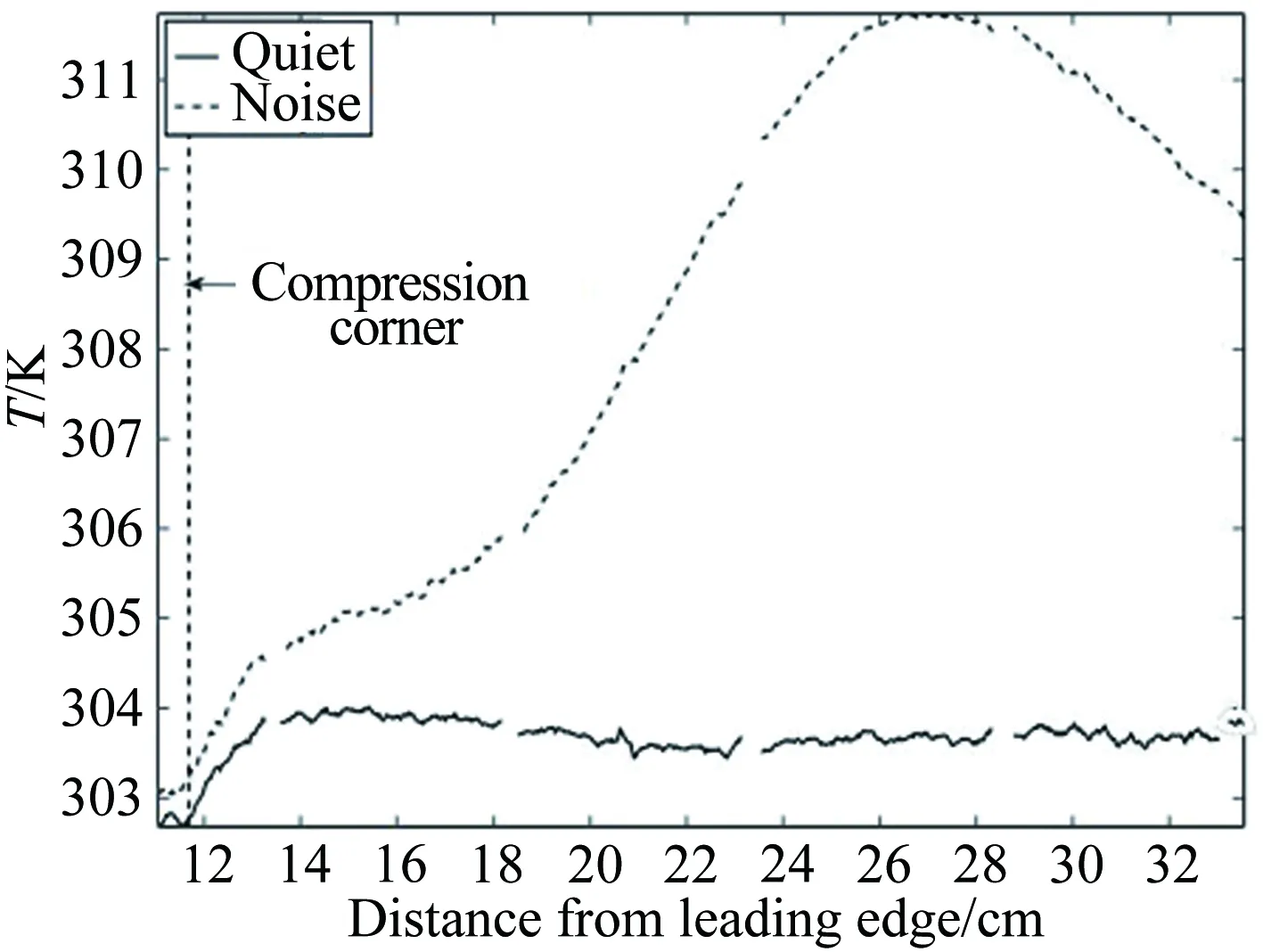
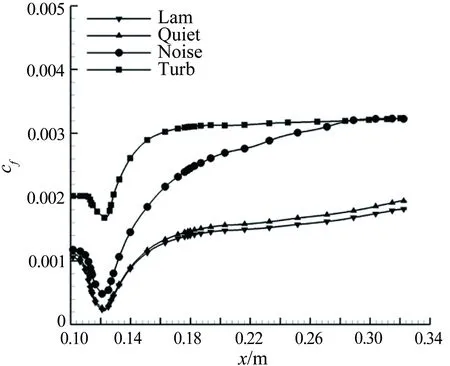
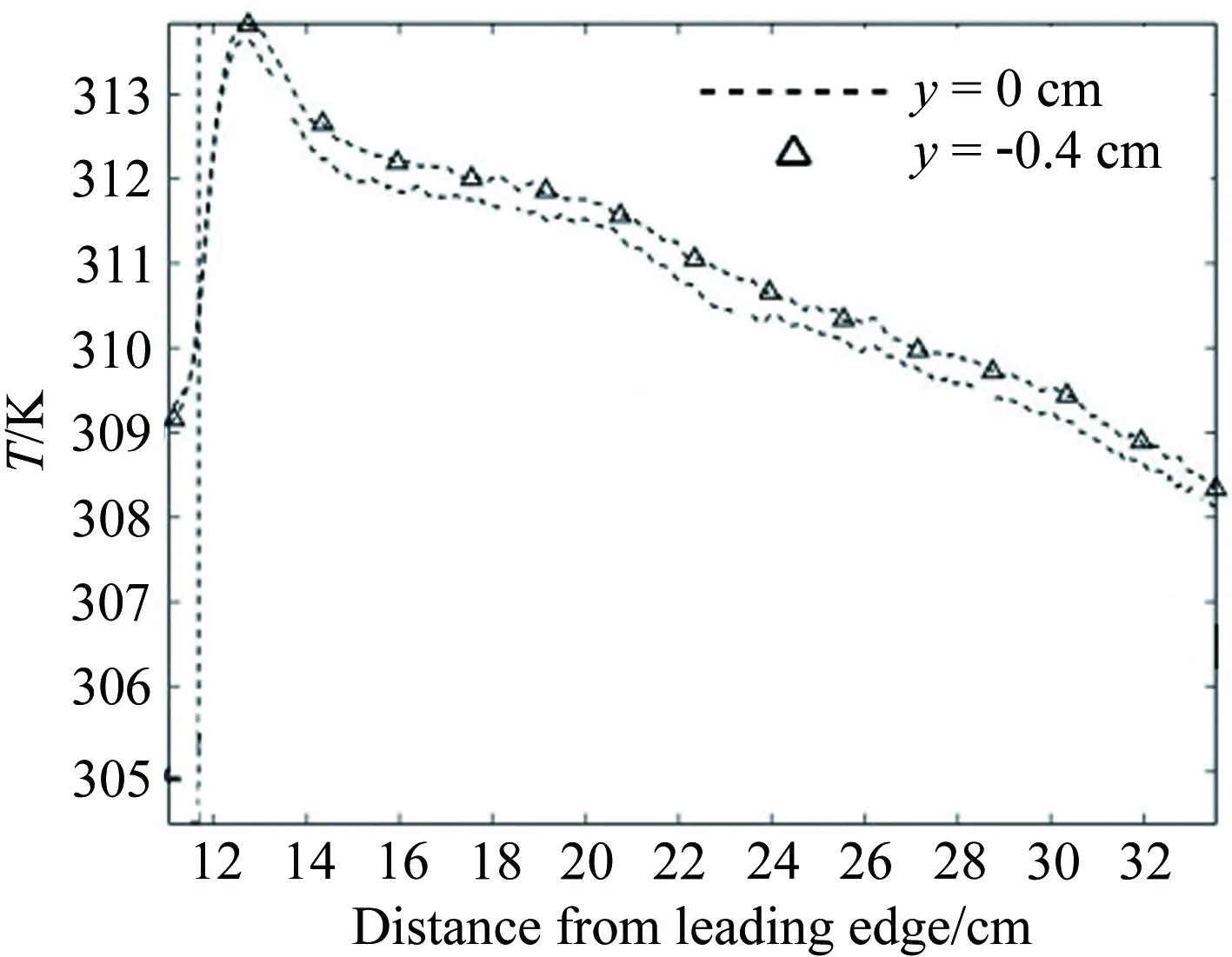
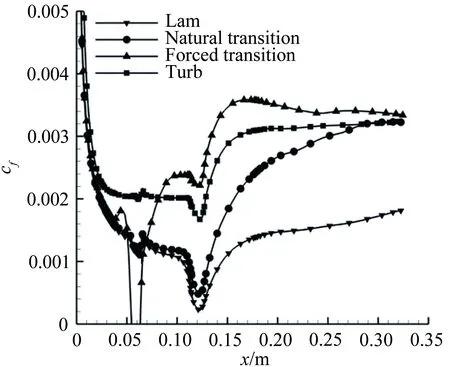
图11为中心线St数分布,对于迎风面,测量到的St数显示转捩大概在距前缘0.25m的位置发生,但是原始的γ-Reθ模型给出的转捩位置却在距前缘0.06m左右,这是由于高马赫数和可压缩性导致了转捩起始动量厚度雷诺数的增加,而这一增加效果在原始的转捩模型中被忽略掉了,因此转捩位置被大大前移。所以原始的转捩模型和全湍流下的 SST 模型均在x=0.25m的上游区域给出了远高于试验值的热流。而本文修改的模型,不仅准确地捕捉到了转捩的位置,壁面热流也与试验吻合较好。转捩结束位置的热流大约是层流区的3倍,并且要稍高于全湍流计算的结果。对于背风面,由于壁面温度与恢复温度比较接近,热流值都比较小,因此不同模型得到的热流相差不大。图12所示为迎风面的St数分布和摩擦力线。原始的γ-Reθ和全湍流 SST 模型给出了相似的St数分布。本文修改的模型计算结果则显示:在上游区域,热流情况基本与层流结果一致, 0.23m 图11 中心线St数分布 Fig.12Stantonnumberdistributionandfrictionforcelinesofthewindward Tirtey和Chazot[25-26]在VKI H3高超声速风洞中对单个粗糙颗粒诱导平板转捩情况进行了一系列试验研究。粗糙颗粒构型包括圆柱形、钻石形、斜坡形和半球形,本文选取圆柱形和钻石形粗糙颗粒在高雷诺数下的情况进行模拟。模型如图13所示,一块长 290mm、宽100mm,前缘钝度 0.5mm的平板,在距前缘60mm处安装了一个粗糙颗粒,粗糙颗粒细节如图13(b)所示,其中a=4mm,对于圆柱形粗糙颗粒,k=1.02mm,对于钻石形粗糙颗粒,k=0.83mm。来流马赫数为 6,来流单位雷诺数为2.7×107/m,来流总压3.1MPa,总温为500K,壁温在试验开始时均为(292±2)K,试验结束后层流区最大温升为4K,湍流区最大温升为12K,由于这里壁温变化都不大,因此选取300K为壁面温度。粗糙颗粒附近的网格如图14所示,第一层壁面y+<1,网格量为500万左右。来流湍流度设为 1.5%。 (a) (b) 图14 粗糙颗粒附近网格示意图 此算例中St数定义为: Tt表示总温,Tw表示壁温。圆柱形粗糙颗粒尾迹区的红外热试验和计算的St数分布对比如图15、16所示,试验和本文修正的γ-Reθ转捩模型均显示粗糙颗粒诱导的尾迹区的热流明显超出了非尾迹区,而对于原始的γ-Reθ模型,尾迹区和非尾迹区均出现了转捩现象,当来流湍流度被修改为 0.5% 时,非尾迹区在下游阶段仍出现了转捩现象,而尾迹区的转捩现象却比试验更靠后。这表明原始的γ-Reθ转捩模型不仅对自然转捩的预测比实际情况早,而且对粗糙颗粒对转捩的促进作用模拟不够。而修正后的模型克服了以上两个缺点,在尾迹区和非尾迹区均给出了与试验吻合较好的结果。将修正后的模型计算得到的尾迹区和非尾迹区的St数取出,与试验值以及非尾迹区的全湍流值进行对比,如图17所示。当流体流过粗糙颗粒后,尾迹区的壁面热流出现了一个快速增长区,之后由于分离涡的作用,其值降低到一个较低值,而后再慢慢增长到全湍流值。St数在尾迹区的值是非尾迹区的2.5~3倍。由于全湍流计算结果中粗糙颗粒后缘的尾迹区也有一个热流值较低的区域,因此可认为转捩在粗糙颗粒后缘就已经完成。试验与计算的对比显示:修正的模型可以模拟粗糙颗粒诱导转捩的整个过程,也能较好地预测壁面热流。但是,在试验中,随着尾迹区的流体向下游流动,非稳定结构在展向发展明显,因此转捩区域越来越宽,而在本文的计算中,转捩区域在展向的发展却比较缓慢。图16(a)、(b)和图17(b)显示的是修改后的模型模拟钻石形粗糙颗粒的情况,结果与圆柱形粗糙颗粒比较类似。 (a) 红外热试验结果 (b) 计算结果 (c) 计算结果 (d) 计算结果 图15 红外热试验和计算得到的St数分布(圆柱形粗糙颗粒诱导转捩) Fig.15Infra-redvisualizationandcalculatedStantonnumberdistributionforcylinderroughnesselements (a) 红外热试验结果 (b) 计算结果 图16 红外热试验和计算得到的St数分布(钻石形粗糙颗粒诱导转捩) Fig.16Infra-redvisualizationandcalculatedStantonnumberdistributionfordiamondroughnesselements (a) 圆柱形粗糙颗粒 (b) 钻石形粗糙颗粒 Fig.17ComparisonofStnumberinandoutofwakeregionforcylinderanddiamondroughnesselements 图18则为粗糙颗粒下游流向涡的发展情况,其中展向切片上显示的是流向涡量的大小|ωx|(只显示了|ωx|>2000s-1的情况)。从图中可知,对于两种形式的粗糙颗粒,下游均发展形成了由粗糙颗粒后缘发展起来的主涡和粗糙颗粒两侧形成的次涡,并在继续向下游的发展过程中慢慢耗散掉,流动则转捩为湍流。但本文的计算结果显示其流向涡破碎之后并没有往展向有明显的拓展,因此转捩区域在展向也并未出现明显的展向拓展,考虑到尾迹导致的转捩位置区域很靠前(图15(a))和很靠后(图15(c))时,尾迹往展向的发展速度均很缓慢,因此这可能是由于计算方法中耗散过大致使未能捕捉到足够的尾迹流动细节造成的。而过大的耗散则是因雷诺平均引入的湍流粘性和MUSCL插值造成较大的数值耗散共同导致的。 (a) 圆柱形粗糙颗粒 (b) 钻石形粗糙颗粒 Fig.18Developmentofstreamwisevortexdownstreamoftheroughnesselements 目前已有的转捩预测方法虽然很多,但是研究的多为平板、圆锥等简单构型,而针对高超声速进气道构型进行完整模拟的还比较少。王亮[27-28]用其提出的三方程转捩模型对X-51A 20%缩比模型在普渡大学Ma6静音风洞中的自然转捩试验结果进行了模拟,结果显示该转捩模型抓住了静音状态下流动一直保持为层流的特征,也较准确地刻画了噪声状态下的转捩起始位置,但是在转捩结束位置上与试验结果还存在较大差别。Orlik[29]则采用了风洞试验与数值模拟相结合的方法,研究了一个高超声速前体的自然转捩情况,其计算采用的是基于线性稳定性分析的eN方法,由于对扰动增长率的积分并不是从中性线上开始的,而是从距前缘1.33mm的固定位置开始,因此积分起始位置的N值是未知的,造成了对N值的刻画出现较大的不确定性。本文希望能够针对进气道模型同时对自然转捩和强制转捩进行模拟,从而考核本文建立的转捩模型对高超声速复杂构型的转捩预测能力。 Brog[30]在 Boeing/AFOSR Mach-6静音风洞中采用 20% 的缩比模型对X-51A进气道转捩情况进行了一系列试验研究。主要研究了噪声对光滑壁面的自然转捩和粗糙颗粒诱导的强制转捩的影响。模型如图19所示。模型总长34.42cm。为评估本文的模型对复杂构型转捩的模拟能力,计算了3个算例,并将计算结果与试验数据进行了对比。计算设置如表3所示。由于没有偏航角,为节省计算量,只计算了一半的模型,在中心面上采用对称边界条件。光滑壁面模型的网格为400万左右,安装了钻石形转捩带的模型网格量为600万左右。壁面第一层网格y+小于 1。试验结果显示壁面温度在整个试验过程中变化很小,因此将壁温设为300K。湍流度在噪声条件下为3.0%,静音条件下为0.05%。由于3个算例的马赫数和雷诺数都非常接近,其壁面摩阻和热流差别也很小,因此在计算全层流和全湍流结果时,只计算了case5,并用其来判断3个算例的转捩位置。 图19 20%缩比X-51A前体构型示意图 CaseMaRe/m-1总压/kPa总温/K来流湍流度转捩类型46.006.59×1065864180.05%自然55.807.40×1066214243.00%自然65.787.35×1066144243.00%强制 图20为噪声情况下模型迎风面测量得到的壁面温度与计算的摩阻系数。试验与计算结果均在压缩拐角之后开始上升,但测量的壁面温度显示转捩位置在中间最靠后,在两侧区域最靠前;而计算结果显示转捩区域在展向分布较为均匀。从图21可知,安装了转捩带后,测量的壁面温度在压缩拐角之前就明显大于光滑壁面情况,计算得到的摩阻系数则在转捩带之后立即上升到较高值,表明转捩位置位于压缩拐角和转捩带之间。 图20 迎风面测量得到的壁面温度和计算得到的摩阻系数(case5) Fig.20Measuredsurfacetemperatureandcalculatedskinfrictionforwindwardsurface(case5) 图22为迎风面 case4~case6的壁面热流及 case5的全层流和全湍流情况。静音条件下,热流分布与层流情况基本一致,表示转捩并没有发生;噪声情况下,拐角之后出现了明显的热流抬升,即转捩现象。而安装了钻石形转捩带之后,转捩位置被推到了转捩带和压缩拐角之间的位置。热流结果与摩阻系数得到的结论吻合。摩擦力线则显示:在层流和静音模式下,由于压力梯度的作用,进气道下表面有明显的横流溢流,会导致进入进气道的流量降低;而对于全湍流或者转捩的状况,这样的横向流动得到了较为明显的抑制,有利于提升进气道捕获流量。在图23中,噪声条件下,计算的中心线热流显示转捩一经过压缩拐角就开始,而在x=0.28m的位置完成。测量的壁面温度显示转捩起始于压缩拐角,结束于x=0.27m的位置。而静音条件下计算与试验结果都显示没有出现转捩现象。在静音和噪声情况下,试验与计算得到的转捩起始和结束位置均吻合较好。图24中,在中心线位置,计算的摩阻系数和测量的壁面温度在压缩拐角的位置均已经超过了光滑壁面的情况,进一步表明边界层在压缩拐角之前就已经转捩为湍流。从计算结果可知,转捩带将转捩完成位置前推到了距前缘0.08m的位置。 图21 迎风面测量得到的壁面温度和计算得到的摩阻系数(case6) Fig.21Measuredsurfacetemperatureandcalculatedskinfrictionforwindwardsurface(case6) 图22 计算得到的迎风面热流对比 (a) 测量得到的壁面温度 (b) 计算得到的摩阻系数 图23 中心线上测量得到的壁面温度和计算得到的摩阻系数(case4, case5) Fig.23Measuredsurfacetemperatureandcalculatedskinfrictionofthecenterline(case4,case5) (a) 测量得到的壁面温度 (b) 计算得到的摩阻系数 图24 中心线上测量得到的壁面温度和计算得到的摩阻系数(case6) Fig.24Measuredsurfacetemperatureandcalculatedskinfrictionofthecenterline(case6) 在 RANS 求解器框架下,通过添加可压缩性修正,修改分离诱导转捩参数,并对经验耦合关系式进行修改,搭建了针对高超声速情况下的γ-Reθ转捩模型。用原始的γ-Reθ模型和修正后的模型对Ma7.4的 Ames 全尺寸模型和Ma6的单个粗糙颗粒诱导平板转捩进行了计算。 结果显示:原始模型在计算自然转捩时,转捩位置过于靠前,而且不能捕捉粗糙颗粒对转捩的促进作用;而修正模型克服了原始模型的这两个缺点,得到了与试验比较一致的结果。最后,将修正后的模型应用于20%缩比X-51A前体进气道模型的自然转捩和强制转捩计算,结果显示模型能够反映高湍流度和粗糙颗粒对转捩的促进作用,表明该模型有望应用于高超声速复杂构型自然转捩和强制转捩的预测研究。 当然,由于该模型目前仅将来流湍流度作为来流扰动条件,而高超声速来流扰动中的湍流度、扰动频率、扰动模态均可影响转捩位置,因此,如何使模型更有效反映来流扰动,特别是来流压力扰动发展成为第二模态后对转捩的影响,有待进一步研究。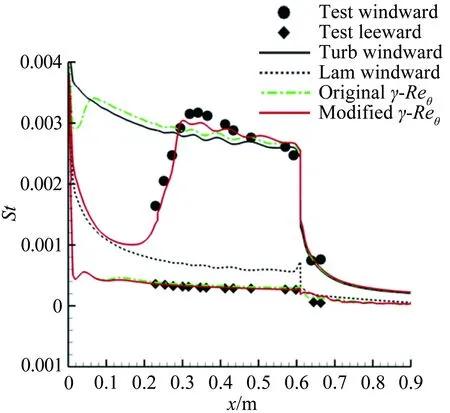
2.2 Ma6平板上单个粗糙颗粒诱导转捩



2.3 20% 缩比X-51A前体模型在BAM6QT中的转捩

3 结 论
