基于图像处理的服装样板轮廓提取

周 佳，宗雅倩，刘其思，徐平华,2，桑振聪

( 1.南通大学 纺织服装学院，江苏南通 226019；2.南通大学 杏林学院，江苏南通 226019 )

服装样板是在现代服装工业生产中进行画样裁剪和产品缝制过程中的依据，也是检验产品规格质量的直接标准[1]。在现代化工业生产中，对外来样板的精确识别需求越来越大，同时对样板尺码缩放等再加工过程的效率提出了巨大的考验。因此，是否能将纸质样板实物快速精准的提取并且转换成为计算机中可编辑的数据形式成为了样板轮廓提取的关键。

本文将通过MATLAB编程，实现样板边缘轮廓的提取、优化，使原本硬质卡纸形式的实物样板转化成理想的计算机样板图。计算机样板图的输出大大减少了服装样板在日常像素储存中所占用的空间，并可将数据传输至AutoCAD软件中进行相应的编辑，给实际工业生产带来了极大便利，服装样板轮廓提取具有重要的研究和市场应用价值。

1 基于总变差的数字图像预处理

由于图像受到各类环境噪声的干扰，图像质量会有一定程度的退化下降。因此，对图像进行降噪处理是十分必要的。在对样板的预处理中，本文将利用总变差模型对图像进行预处理，将干扰项消隐，最终使得样板图像具有更清晰的视觉效果。

一幅受到干扰的图像可以分解为图像U和加性随机噪声W。

其中加性随机噪声是一种高斯白噪声，具有零均值，方差为σ2，并且包含噪声的图像的全变分比无噪声的图像明显加大，最小化全变分可以消除噪声[2]。

图像U的全变分定义为梯度幅值的积分形式：

(1)

(2)

因此，约束项的选取尤为关键。.

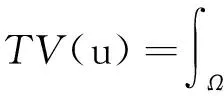
(3)

以下图中服装样板图像为例(图1所示)，图1(a)样板中含括了一些无价值的线条信息，通过算法对图像进行消隐去噪后，得到图1(b)，可以消除干扰线条，获得更清晰的服装样板。

图1 服装样板(a)及去噪效果图(b)

2 利用Canny算子对样板进行边缘检测

图案的边缘提取问题，即根据图像亮度信息提取和表示出具有显著变化的位置，最后保留图像的主要结构信息[4]。而服装样板的边缘提取也属于这类问题。常见的边缘检测算法包括Roberts边缘检测、Sobel边缘检测、Prewitt边缘检测等，但都或多或少地存在着一定的问题。如Roberts算子虽然简单明了,运行快速且方便，尤其是对具有陡峭的低噪声图像的反应最好,但结果中会存在伪边缘，不能够如实地反映服装样板的真实情况；Sobel算子和Prewitt算子虽然检测边缘的范围更广，但也存在着伪边缘，而且检测出来的边缘线较粗，更放大了噪声[5]。在相对复杂的图像中使用这些算法，会使得结果出现更明显的断点，且无法完全提取出服装样板。而Canny算子则在以上方面表现较为出色。因此，本文经过比较分析后，最后利用Canny算子对预处理后的图像进行边缘检测。主要步骤如下：

(1)去噪声。对于没有经过处理的原始图像，任何边缘检测算法都用之无效。因此，要对样板图像进行最初的去噪或杂质消隐处理，本文利用之前提到的总变差图像滤波处理来对原始样板图像进行去噪处理。

(2)梯度计算。利用导数算子找到图像灰度沿着两个方向的导数GX、Gy，然后就可以分别求出梯度的幅值和方向[6]：

(4)

(5)

(3)梯度方向确定。首先，获得图像的边缘方向，并将模板边缘的梯度方向粗略地划分为若干个角度，并根据角度找到像素梯度方向的相邻像素。

(4)遍历图像。如果像素的灰度值与梯度方向上的两个像素的灰度值相比不是最大的，则像素的灰度值被设置为0，即该像素点位置不是边缘[7]。

(5)用累计直方图计算两个阈值。任何大于高阈值的像素点位置一定是边缘，反之同理。如果检测结果在高低两个阈值之间，判断在像素的相邻像素中是否存在超过高阈值的边缘像素，如果有的话则是边缘，反之则不是[8]。

3 样板边缘骨架细化

骨架是可有效地反映出原物体形状的连通性和拓扑结构而由单个像素点组成的重要几何特征。通常，获取图像骨架的过程即是“细化”图像的过程。使用对象的骨架来描述对象是一种强调对象的结构特征并提高内存使用和数据压缩率的好方法[9]。在本文中利用MATLAB的骨架提取算法，将经过形态学修复的样板轮廓进行骨架提取，使其细化为一维曲线，便于样板数据的矢量化存储。

3.1 基于数学形态学的边缘骨架提取

在利用改进的Canny算法提取样板边缘后，基于数学形态学提取边缘骨架。数学形态学的骨架化方法，是基于数学图论的学科，主要思想是通过一定形态的结构元素测量和提取图像中的相应形状，以便进行图像分析和识别[10]。图像经过数学形态学的处理，不但可以使原图像数据信息简单化，而且可以去除不相关的信息，保留根本的形状属性，并且具有原生的并行实现的结构优点，最后得到连续、准确的骨架。

根据最大圆盘算法的定义，两组结构元素分别为：

A={A1,A2,A+3,A+4},B={B1,B2,B3,B4} (6)

前者用于去除西北、东北、东南和西南角的点，后者用于去除北、东、南和西方向上的点，如图2所示。在图中，＊表示被引用的中心点，1表示目标图像的点，0表示背景图像，x表示目标图像或背景图像[11]。

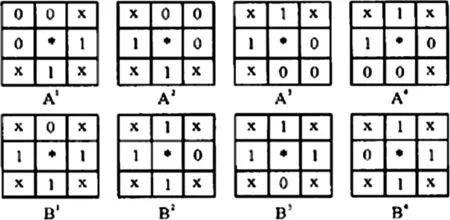
图2 结构元模板

3.2 骨架细化处理

结构元B对集合A的细化可表示为A⊗B,它可以根据命中或未命中变换来定义：

A⊗B=A-(A⊗B)=A∩(A⊗B)C

(7)

通过应用数学形态学细化算法来细化图像，主要步骤如下：

(1)目标图像A细化成Y，用A→Y；

(2)作A=A⊗Bi，其中i从1取到8；

(3)如果A=Y，迭代结束，否则执行步骤(4)；

(4)A←Y，再执行(2)步骤。

经数学形态学细化后的样板骨架如图3所示，得到单像素连通的样板骨架，大大缩减了样板的存储量。

图3 样板骨架

3.3 轮廓边缘优化

边缘的完整性对后期图像的处理起到关键作用。因此，对分割后的图像进行修复就显得十分重要。本文利用形态学运算来修复边缘图像。形态学运算主要包括开运算和闭运算[12]。

先进行腐蚀而后膨胀的过程称为开运算。结构元B对集合A的开操作，表示为A∘B，定义如下：

A∘B=(AΘB)

(8)

先进行膨胀而后腐蚀的过程称为闭运算。结构元B对集合A的闭操作，表示为A·B，定义如下：

A·B=(A⊕B)ΘB

(9)

具体以下图为例，图4中(a)图为对样板进行预处理，边缘提取和骨架细化后的图，由于样板边缘相隔较近，导致出现连接现象，而且在样板边缘出现凸起、不平整等现象。通过形态学运算，将图4(a)中的问题进行了较好的修复，如图4(b)所示，最终能够输出光滑连续的曲线，这为后续操作提供了坚实的基础，具有重要意义。

(a) (b)

4 矢量化数据格式输出

由于样板轮廓将会被运用到工业制版中，因此需将所得到样板轮廓通过图形交换文件保存为AutoCAD能够识别的格式DXF，以便后续处理。DXF是Autodesk公司为了在AutoCAD与其它软件之间交换CAD数据而开发的CAD数据文件格式[13]。

在制版过程中，大多使用AutoCAD进行制版，且DXF格式文件中代码本身就具有良好的可读性，方便用户修改。因此，本文将所得样板轮廓保存为DXF格式，最后利用VisualC++编制程序，将保存DXF格式的矢量化数据传输到CAD制版系统中。

5 实验结果及分析

本文采用MATLAB编程，选用普通服装样板作为测试样，利用上述方法进行服装样板轮廓提取、优化。图5(Ⅰ)为分割后的样板边缘，图5(Ⅱ)为骨架提取细化后的样板轮廓，图5(Ⅲ)为优化后的样板轮廓。

Ⅰ 样板边缘

Ⅱ 样板骨架轮廓

Ⅲ 样板轮廓优化

从实验结果中，可以看出改进的Canny算法能够较为准确完整地分割出样板的边缘，在提取边缘轮廓的骨架并细化时，可以从结果中看到虽然提取出的骨架具有一定的连贯性，但是在骨架的若干部位还存在一定的奇异点及凸起；而在轮廓优化中，则很好地解决了这一问题，使得单像素样板轮廓连贯准确。

6 结语

本文采用MATLAB编程，利用改进的Canny算法用于检测和分割平滑处理后的服装样板，并利用骨架提取算法来细化样板的轮廓。在实际应用中有很大的应用价值。而样板轮廓的提取输出则大大减少服装样板原始存储中所占用的存储空间，并可将数据传输至AutoCAD软件中进行相应的编辑，带来了极大的便利。