基于局部敏感哈希的导航星库快速搜索算法
2018-11-14朱海龙梁斌张涛
朱海龙, 梁斌, 张涛
(清华大学 自动化系, 北京 100084)
星敏感器具有姿态测量精度高、自主工作能力强和可靠性高等优点,已经成为各类航天器首选姿态测量设备。根据工作场景不同,星敏感器的工作模式可以分为全天球自主工作模式和星跟踪模式2种[1]。在初次进入工作状态或者故障恢复后,星敏感器没有任何先验姿态信息,进入全天球自主工作模式。此时星敏感器通过其光学系统获取星图,计算出星点在星图中位置,然后构造出识别模式,并且与导航星数据库中存储的识别模式进行搜索匹配,识别出星图中的导航星,进而确定航天器瞬时姿态信息。在得到先验姿态信息后,星敏感器就进入星跟踪工作模式,此时星敏感器可以利用在全天球自主工作模式下获取的先验姿态信息和航天器的运动方程,快速更新航天器姿态信息。可以看出,如何在全天球自主工作模式下准确快速地识别出导航星是星敏感器稳定可靠工作的关键。
目前,已经有许多全天球自主工作模式下的星图识别算法提出,典型的算法有三角形识别算法[2]、Pyramid识别算法[3]和栅格识别算法[4]等。在这些算法及其改进算法中,导航星数据库的搜索速度是决定星图识别算法效率的核心因素。Liebe提出的三角形算法中选用"边角边"识别模式,直接建立星图识别数据库,通过直接遍历搜索进行星图识别[5]。由于三角形识别模式维度较低,在导航星数量多的情况下会导致误匹配率高和识别速度慢。为提高星图识别的鲁棒性,Mortari等人提出Pyramid星图识别算法,通过增加一个角距来判断星图识别的唯一性。为了提高星图识别速度,Mortari等人对星角距升序排列,提出k-vector区域搜索算法[6],该算法的搜索速度比遍历查找算法提高了10~50倍。张广军等人提出基于径向和环向特征的星图识别算法[7],该算法在星点位置误差1个像素的情况下识别成功率达到97.57%,并且通过线性数据库搜索方法,提高了星图识别速度。江洁等人对张广军等人提出算法进行改进[8],提出冗余径向和环向特征识别模式,通过冗余编码方式,降低星等和星点位置噪声对星图识别的影响,但是在识别速度方面略慢于张广军等人提出的算法。杨君等人通过2级压缩技术将导航星分布的二维数组压缩成一维数组,然后建立Hash映射实现导航星表快速搜索,实现了导航星表的无冗余存储,提高导航星的搜索速度[9]。张磊等人在改进三角形识别算法过程中,用哈希方法散列星角距和相对星等差,提高了识别速度[10]。熊雪等人在研究多视场星图识别技术中,利用哈希查找的方法快速访问分块存储的星对角距,识别速度提高了11倍左右[11]。Rao等人利用星角距值在坐标系 轴的投影建立哈希函数,进而提高星角距数据库的搜索速度[12]。郭磊利用双哈希表方式存储和访问导航星数据库,利用拉链法处理冲突,降低哈希表冲突率,并提高了搜索速度[13]。利用哈希表建立和访问导航星数据库,时间复杂度能够达到O(1),明显优于遍历查找方法、二分查找方法和k-vector区域搜索方法,这些方法的时间复杂度分别是O(n),O(log(n))和O(k)。但是哈希搜索算法是一种典型的空间换时间的方法,导航星数据库的存储量会随着访问时间的降低而快速增加。因此如何在提高导航星数据库搜索速度的同时尽可能降低导航星数据库的存储容量,是本文主要的研究方向。
由于星图成像存在各种噪声,在已有的星图识别算法中,通常是建立“一对一”的星图识别模式数据库,即在星图识别数据库中有且仅有一个识别模式与星图中构造的识别模式对应匹配。因此,这种方式建立的数据库在受到噪声影响时,不仅影响星图识别成功率,还影响星图识别速度。本文选用有序星点集作为星图识别模式,考虑角距误差对星图识别速度的影响,提出基于局部敏感哈希的快速星图识别算法,以角距误差限为基准对星图识别数据库中星角距进行量化,建立实际角距与待匹配角距之间的映射关系,利用整数哈希函数散列得到的映射值,把每个识别模式的中心星点对应的编号对应于多个哈希值,建立“一对多”的星图识别模式数据库,即在星图识别数据库中,存在多个识别模式与星图中构造的识别模式匹配,可以有效提高星图识别的速度。
1 导航星库构建
星图识别模式及其数据库是影响搜索速度的基础因素,本文选用有序星点集(ordered star points set,OSPS)作为星图识别模式,建立星图识别数据库。
1.1 有序星点集星图识别模式
星点s0的有序星点集星图识别模式如图1所示,定义pat(s0,S,Fi)(i=0,…,k)为星点s0的有序星点集星图识别模式,其中s0为主星点,S为主星点s0的有序星点集,Fi(i=0,…,k)为S中每个星点的特征。

图1 有序星点集星图识别模式
在选定主星点s0后,利用s0近邻算法,选取s0(s0小于星敏感器视场角的一半)范围内到星点s0最近的s0颗星,选择s0颗星中距离星点s0最近的星为参考星点s0。以s0为起点,按照顺时针顺序对s0颗星排序,就可以得到星点s0的有序星点集s0。对于s0中每个星点s0,都可以用星点之间的角距表示其特征s0。可以分为以下几种情况:
1) 主星点s0的特征为F0={e0,i}(i=1,…,k);
2) 参考星点s1的特征为F1={ek,1,e0,1,e1,2};
3) 星点si(2≤i≤k-1)的特征为Fi={ei-1,i,e0,i,ei,i+1}
4) 星点sk的特征为Fk={ek-1,k,e0,k,ek,1}
其中,e表示星点之间的距离星角距,下脚标表示星点的编号。按照星点有序集S中星点的顺序把每个星点的特征Fi组合起来,就可以得到星点s0的有序星点集星图识别模式pat(s0,S,Fi)(i=0,…,k)。
1.2 星图识别数据库
在星敏感器光电系统探测范围内,按照一定原则筛选后的恒星是可用于星图识别的导航星。假设可用于星图识别的导航星的数量为M,按照恒星编号顺序排列后,可以得到星敏感器的星图识别数据库如图2所示。其中第1列为主星点的编号,第2列和第3列分别是主星点的赤经和赤纬,第4列为主星点的有序星点集模式特征F(i)(i=1,…,M)。

图2 有序星点集星图识别数据库
根据1.1节对有序星点集星图识别模式的定义,星角距存在重复现象。因此,为了降低星图识别数据库的存储量,每个星点的有序星点集模式特征F(i)的存储格式如图3所示。其中,k表示主星点s的最近邻星点数量,Di(i=1,…,k)表示每颗近邻星点的信息,包含星编号、到主星点的角距e0i和到下一颗近邻星点的角距ei,i+1。

图3 单星点有序星点集识别模式存储格式
2 局部敏感哈希快速搜索算法
星图识别的本质是在星图识别数据库中搜索匹配星图中构造的识别模式,由于导航星数量众多且每个星图识别模式中包含多个星点特征,因此需要设计快速搜索算法提高星图识别速度。此外,由于实际星图中获得的识别模式存在误差,因此可以把星图识别模式在星图识别数据库内的搜索匹配过程认为是最近邻搜索问题。本文提出适用于星图识别数据库快速搜索的局部敏感哈希算法,可以在存在误差的情况下,快速搜索匹配星图识别模式,进而识别出导航星,提高星图识别速度。
2.1 星图识别局部敏感哈希映射原理
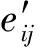
(1)
式中,n′和n分别表示实际角距与理想角距对应的量化值,则当n′∈{n-1,n,n+1}时,就可以认为该星角距匹配成功。假设有N个角距同时匹配成功时可以认为该星图识别模式匹配成功,则在星图识别数据库中就会存在有3N个星角距量化值组合判定星图识别模式匹配成功。

图4 局部敏感哈希映射原理示意图

2.2 哈希表建立过程
根据所需要识别的角距数量的不同,可以把星图识别数据库中的星图识别模式组合成3N个可以匹配的识别模式。图5给出了利用局部敏感哈希原理对星图识别数据库内识别模式的哈希表建立过程,具体的实现过程如下:
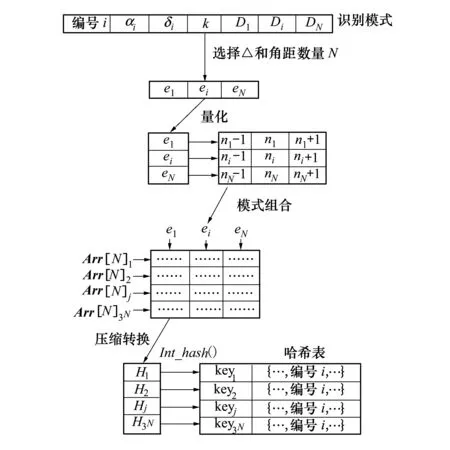
图5 星图识别数据库哈希表建立过程
1) 选择星图识别的角距误差限Δ和需要识别的角距数量N;
2) 在星图识别模式中,选择需要量化的N个角距,并且按照公式(1)进行量化,得到量化后的角距值n1,…,ni,…,nN;
3) 把每一个角距量化值集合{ni-1,ni,ni+1}按照角距选择顺序排列组合,然后以16位形式存储到数组Arr[N]i中;
4) 为了压缩存储空间,把Arr[N]i中的数利用CRC32转换为32位整数Hi
5) 采用整数哈希函数对Hi进行散列,每个哈希表key值对应的value是有序星点集模式的中心星点对应的星编号的集合,即
(2)
在角距量化的过程中,每一个角距通过公式(1)转换为一个16位的整数,在选择N个量化角距的情况下,量化后的识别模式需要占用的存储空间为16×N位,因此为了压缩存储空间,本文采用了CRC32编码的方式,把量化后的识别模式Arr[N]i转换成32位的整数Hi。然后,本文引用STLport 5.2版本中的整数哈希函数,把由识别模式转换得到的32位整数Hi散列到哈希表中。
按照上述哈希表的建立过程,对每个导航星对应的星图识别模式逐个转换,就可以建立星图识别数据库对应的哈希表。
2.3 哈希表搜索过程
建立了星图识别数据库以及对应的哈希表之后,就可以进行星图识别。在得到实际星图后,通过星点质心定位算法确定星图中恒星的位置,构造每个星点的有序星点集识别模式,然后按照局部敏感哈希映射原理,得到有序星点集识别模式对应的哈希值,在星图识别数据库内搜索匹配,完成星图识别。具体的哈希表搜索过程如图6所示。

图6 哈希表搜索过程
具体的搜索过程可以表示为:
1) 在星图中构造有序星点集模式,并选择其中N个角距作为搜索特征;
2) 以Δ为基准量化N个选定角距,然后按照顺序存入对应的数组Arr[N]′中;
3) 把Arr[N]′利用CRC32方式编码压缩,得到对应的32位整数H′;
4) 采用建立哈希表时使用的整数哈希函数对H′进行散列,得到对应的哈希值key′;
5) 查找导航星数据库哈希表,是否存在与key′对应的哈希值。若不存在,则识别失败。如果存在,检查此哈希值对应的星编号集合是否唯一,如果唯一,则星图识别成功;如果不唯一,则在对应的集合内进行线性搜索,进行星图识别。
在建立的星图识别数据库哈希表中,每一个星图识别模式都存在多个哈希值。通过建立这种“一对多”的星图识别方式,可以在星图识别模式存在误差的情况下,快速匹配星图识别模式,识别出导航星。
3 仿真实验结果与分析
3.1 仿真条件
仿真实验中选择Sky2000星表中亮度高于7.0等星作为导航星,共有11 003颗导航星,建立有序星点集识别模式的半径为r=5°,仿真计算机的CPU为Intel Core i7-4770MQ,仿真环境为Microsoft VS2008,其他仿真参数如表1所示。

表1 仿真实验参数
通过蒙特卡罗方法随机生成1 000个视场指向并仿真星图。根据分析可知,角距误差限Δ和需要识别的角距数量N是影响哈希表最主要因素。根据仿真条件可知,单个像元对应的角距为:
(3)
仿真中以像素对应的角距为基准进行量化。在哈希表中,如果哈希值对应的主星点编号不唯一,定义此哈希值存在冲突,定义存在冲突的哈希值数量与占总哈希值数量的比值为冲突率。
3.2 仿真结果
星角距误差限和选择匹配的星角距数量是影响本文算法的主要参数。利用本文提出的算法,对仿真生成的1 000幅星图进行识别,可以得到在不同角距误差限和选用不同角距匹配数量情况下的结果如表2~表4所示。

表2 Δ=epixel条件下不同角距数量的仿真结果
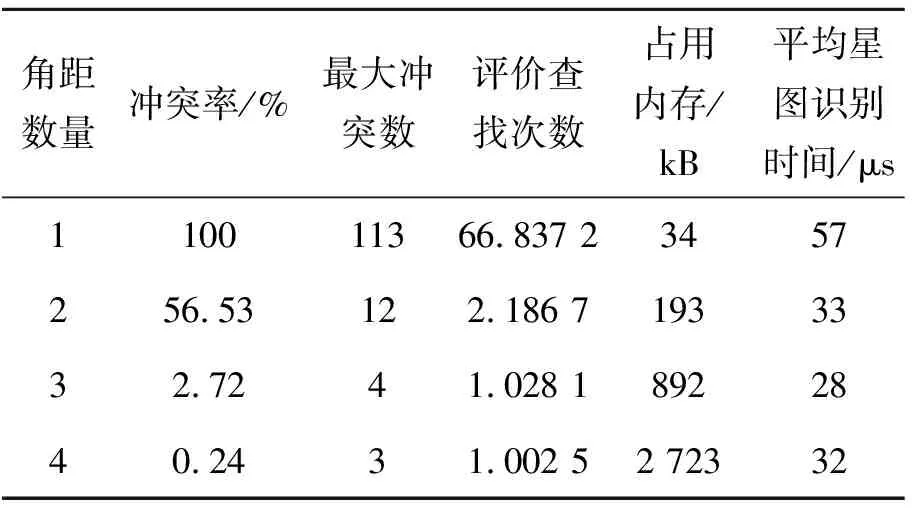
表3 Δ=2epixel条件下不同角距数量的仿真结果

表4 Δ=3epixel条件下不同角距数量的仿真结果
通过仿真结果可以看出:
1) 在同样星角距误差限的情况时,选用星角距的数量为N=1和N=2时,虽然哈希表占用存储空间比较低,但是哈希表的冲突率比较高,最大冲突数量也比较高。在N=3和N=4时,哈希表的冲突比较低,每个哈希值最大冲突数量为3,平均查找次数基本接近与1,但哈希表占用存储空间比较大;
2) 在选择同样匹配星角距数量情况下,随着星角距误差限的增大,哈希表冲突率、最大冲突数量、平均查找次数增多、哈希表占用的存储空间以及平均星图识别虽然都是呈现递增的趋势,但是影响不显著。
3.3 仿真结果分析
通过仿真结果可以看出,角距误差限Δ在不同的情况下,对搜索速度结果影响不显著。因此本文提出算法可以提高星图识别对角距误差限的容忍能力和鲁棒性。在选择角距数量N=1和N=2时,由于存在比较高的冲突率和最大冲突数量,不适合选择建立哈希表。在N=4的情况下,哈希表的冲突率和最大冲突数量都是最低的,但对应的哈希表占用存储空间也非常大。虽然在N=3的情况下建立哈希表的冲突率相对于N=4的情况下略高,但是最大冲突数、平均查找次数以及平均星图识别时间都非常接近,而且哈希表占用的存储空间仅为N=4的情况下的30%,因此选择N=3是比较适合建立导航星快速搜索哈希表。
本文提出的局部敏感哈希搜索算法的时间复杂度为O(1),与传统哈希算法相同。但是传统算法建立的是星图识别模式中角距对应的哈希表,因此对整个星图识别模式匹配过程,至少需要完成多个角距的搜索匹配。本文提出算法则需要完成一次搜索就可以完成星图识别模式的匹配。虽然本文提出算法在时间复杂度上与传统哈希算法一样都是O(1),但是在星图识别过程中,本文提出算法的识别速度优于传统哈希算法。在星图识别模式中需要匹配角距数量N=3的情况下,本文搜索算法与传统哈希算法的对比结果如表5所示。

表5 哈希搜索算法性能对比分析
4 结 论
星敏感器是以恒星为探测目标的高精度姿态测量设备,具备独独立自主工作能力强和可靠性高等有点,已经广泛应用在各类航天器。其中星图识别是影响星敏感器获取初始姿态速度的关键步骤。基于传统哈希算法的星图识别算法是目前已有算法中识别速度最快的,为进一步提高星图识别速度,本文提出基于局部敏感哈希的快速星图识别算法,在考虑星图识别误差的影响情况下,建立星角距的局部敏感映射关系,以星图识别角距误差限为基准,量化星图识别模式中角距,利用整数哈希函数建立“一对多”的星图识别模式哈希表,可以通过哈希表直接快速匹配星图识别识别模式,提高星图识别速度。总体上讲,本文提出的基于局部敏感哈希的快速星图识别算法具有以下特点:
1) 虽然本文提出算法的时间复杂度与传统哈希算法相同,但是在需要匹配同样星角距数量情况下,本文提出算法的识别速度比传统哈希算法快3.4倍左右,哈希表占用内存量约为传统哈希算法1.3倍;
2) 本文提出快速星图识别算法在识别速度方面有很好的鲁棒性,受到星角距误差影响比较小;
3) 考虑工程应用的情况,可以选择星角距误差限为1个像素对应角距,角距数量N=3,此时星图识别过程中哈希表的冲突率为0.74%,平均搜索次数为1.007 4,星图平均识别时间22 μs,哈希表存储容量904 kB。
