基于Peters-ONERA模型的失速颤振特性研究

2018-11-14梁佳骅白俊强李国俊

西北工业大学学报 2018年5期

梁佳骅, 白俊强, 李国俊

(西北工业大学航空学院, 陕西西安 710072)

失速颤振是一种气动弹性失稳现象,常见于高空长航时(HALE)飞行器的大柔性机翼、直升机的桨叶以及涡轮机的叶片上[1]。失速颤振现象不仅会降低飞行器的气动效率,而且会导致结构的疲劳甚至破坏。由于失速颤振常常伴随着以流动分离为特征的动态失速现象,因此具有很强的气动非线性[2]。考虑到失速颤振问题存在着复杂的非线性因素以及研究人员对失速颤振机理缺乏深入的理解,因此有必要对失速颤振问题开展更加深入的研究工作,以便为失速颤振主动控制提供理论基础和技术支撑。

在当今的气动弹性研究领域中,将计算流体力学(computational fluid dynamics,CFD)与计算结构力学(computational structure dynamics,CSD)耦合是进行非线性颤振分析的重要手段之一[3]。然而由于实际工程问题的复杂性,所构建的物理模型往往十分复杂,CFD/CSD方法存在耗时长、效率低等劣势[4],而其中主要的计算代价来源于非线性气动力的求解。这使得CFD/CSD方法难以广泛适用于失速颤振的研究工作中。

为了简化气动力,Peters等人[5]基于Glauert分解方法发展了非定常气动力的有限状态(finite-state)理论和入流(induced-flow)理论。相比其他气动力模型,该方法计算精度较高,工程实际应用性较强。此外,该方法具有时域表达形式,可以加入动态失速修正项来模拟非线性气动力。当前针对二维翼型已经提出了一些较为成熟的半经验失速模型,例如ONERA失速模型和Beddoes-Leishman失速模型等。文献[2]总结了当前工程和研究中常用的失速模型,其中ONERA模型形式较为简单,应用较为广泛。ONERA模型通过适当的线性有理近似,将动失速气动力表达为一个二阶非线性常微分方程的形式。此外,ONERA模型以线化气动力系数和静态气动力系数之差作为输入量,可以描述气动力的延迟效应和超调效应。

Peters等人[6]采用ONERA失速模型对直升机叶片的动态失速问题展开了研究。Mcalister等人[7]基于ONERA失速模型对二维翼型动态失速中的非定常气动力响应进行预测,并与实验值进行对比。大量研究结果表明ONERA失速模型可以较好地模拟动态失速中的非定常气动力。Tang等人[8]通过引入小角度假设,将ONERA模型转化到拉氏域中获得线性非定常气动力,并从频域角度对失速颤振问题展开研究。研究结果表明气动弹性系统在大攻角下的失稳模态发生了转换,但研究人员并未对此开展更加详细的机理解释。Laxman等人[9]基于ONERA失速模型对二元机翼的混沌响应特性进行研究。Beedy等人[10]基于谐波分解方法和Levenberg-Marquardt非线性最小二乘法,发展了一种拟合ONERA非线性参数的新方法,并基于此进行失速颤振边界的预测。

在国内,刘湘宁等人[11]采用ONERA失速模型,结合谐波平衡法,研究了大展弦比复合材料机翼的颤振稳定性。刘廷瑞[12]采用ONERA失速模型,基于H∞鲁棒控制进行风轮机叶片的失速颤振抑制研究工作。任勇生等人[13]采用ONERA模型进行了复合材料薄壁梁的非线性气弹稳定性研究工作。孙智伟等人[14]首次综合考虑了Peters气动力模型和ONERA失速模型,提出了一种新的适用于失速颤振研究的气动力模型,并结合鲁棒控制开展了颤振抑制方面的研究工作。

上述大多是基于ONERA失速模型开展的失速颤振边界预测和主动颤振抑制研究工作,鲜有研究工作者基于Peters-ONERA模型,对大攻角下的失速颤振临界特性和不同初始攻角下气动弹性系统的分岔现象展开研究。此外,基于Peters-ONERA模型对失速颤振中静气弹求解稳定性的研究工作也很少见。本文基于Peters-ONERA气动力模型,建立了系统的状态空间方程。首先通过动态失速算例验证了气动力模型,并研究了亚松弛迭代对静气弹求解稳定性的影响;其次通过频域方法对大攻角下的失速颤振临界特性展开研究;最后通过时域方法研究了失速颤振中的极限环振荡和分岔现象,并研究了初始扰动对系统响应的影响。

1 气动力建模

本节基于Peters气动力模型和ONERA失速模型分别对线性气动力和非线性气动力进行建模。由于上述气动力模型都具有时域表达形式,因此易于和结构运动方程耦合,形成完备的状态空间形式。

1.1 Peters线性模型

图1展示了一个具有两自由度的典型二维翼型。其中Q为气动中心,P为刚心,G为重心。结构坐标系参考原点取在刚心P处,浮沉位移h向下为正,俯仰位移θ抬头为正。刚心P在翼型弦长中点后ab处,其中a为无量纲长度,b为半弦长。

图1 典型两自由度二维翼型

气动弹性系统关于弹性轴的升力和力矩的线性部分如下[15]:

(1)

在方程(1)中,ρ代表大气密度,U为无穷远来流速度,α0代表翼型的初始迎角。在线性升力L0的表达式中,第一项为无环量升力,其依赖于翼型的速度与加速度;第二项为有环量升力,其通过λ0考虑了翼型后缘尾涡的影响。其中λ0表示平均入流诱导速度,Peters将其近似用有限个入流状态量来表示[5]:

λ0=0.5bTλ

(2)

式中，λ满足如下微分方程[15]:

(3)

1.2 ONERA失速模型

在ONERA模型中,Γn(n代表升力L或者力矩M)表示由于失速带来的附加环量,可以通过二阶常微分方程表示。需要指出的是,方程(4)的力矩参考点是翼型的四分之一弦长位置。

(4)

在方程(4)中,气动力的非线性特性可以通过输入值ΔCn(n代表升力L或者力矩M)得到。而ΔCn是关于攻角α的函数,一般通过实验方法或者CFD方法得到。半经验参数ξn,ωn和ηn(n代表升力L或者力矩M)分别代表了气动力阻尼、频率,以及气动力延迟。参数可以表示成如下形式(n代表升力L或者力矩M):

ξn=ξ0+ξ2(ΔCn)2

ωn=ω0+ω2(ΔCn)2

ηn=η0+η2(ΔCn)2

(5)

为了得到方程(5)中各个系数的典型值,必须基于某个特定翼型的实验结果或CFD结果进行参数辨识。Beedy等人[10]认为由非定常升力响应数据拟合得到的非线性参数可以用于非定常力矩的预测。如表1所示,给出了部分ONERA非线性参数的典型值[16],其中Ma代表无穷远来流马赫数。

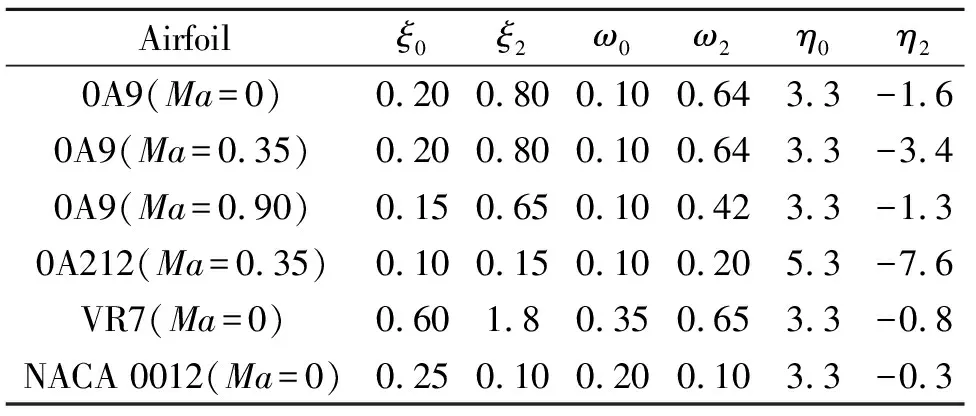
表1 ONERA非线性参数的典型值

综合以上讨论,可以得到气动弹性系统关于弹性轴处的总升力和力矩:

(6)

式中,Cl0和Cm0表示在零攻角下翼型的升力和力矩系数,L0和M0为气弹系统关于弹性轴升力和力矩的线性部分,具体形式可参照(1)式。

孙智伟[17]认为,忽略阻力不会对动力学特性的定性分析产生较大的影响;张健等人[18]指出,如果不需要精确地预测颤振边界和系统极限环响应,可以忽略阻力因素。本文中没有考虑阻力因素,可以在一定程度上简化气动力模型的复杂程度。

2 气动弹性系统求解方法

对于图 1所示的气动弹性系统,基于Lagrange方程可以得到结构运动方程的矩阵形式表达如下[19]:

(7)

式中,M代表质量矩阵,G代表阻尼矩阵,K代表刚度矩阵,δ代表广义位移,f代表作用在系统上的广义力。

为了得到气动力控制方程与结构运动方程的全耦合形式,便于失速颤振问题的分析,将广义气动力f写成如下的矩阵表达形式[14]:

(8)

式中，δ代表广义位移。

(9)

在方程(9)中,矩阵H0和H1的阶数和λ的维数有很大关系。为了保证计算的精度,λ的维数可以取4～8[5],但λ的维数取得过大可能会导致数值不稳定[20]。文献[14]建议取维数n=6。

方程(9)即为气动弹性系统状态空间方程的完整形式。从时域分析的角度来说,此问题转化为一阶非线性常微分方程组的求解问题,可以选用多种求解技术,本文采用欧拉预估-校正方法进行时域推进求解;从频域分析的角度来说,此问题转化为矩阵特征值的求解问题,本文通过求解矩阵H1的特征根得到了系统的特征根轨迹。值得注意的是,由于矩阵H1是一个非线性矩阵,因此为了进行根轨迹分析,需要对矩阵H1进行线性化处理。本文采用雅克比矩阵法对H1进行线性化处理。

3 算例分析

3.1 动态失速算例验证

Mcalister等人[7]指出,在减缩频率k小于0.15的情况下,ONERA失速模型对非线性气动力的模拟具有一定的可信度。对于更高的减缩频率,工程上一般不给予考虑,因为实际机翼也很难达到如此之高的振动频率[17]。

图2 升力系数迟滞曲线对比图(α=10°+15°sinωt)

本文选用减缩频率k分别为 0.1和0.05的2个算例进行研究,采用欧拉预估-校正方法对气动力进行时域推进求解。图2给出了数值解和实验值对比图。由图2可知,当减缩频率为0.1和0.05时,数值模拟结果在上、下行与实验值吻合较好。此外,该模型对失速攻角位置的预测能力具有一定的可信度。这与Mcalister等人得到的结论是一致的。然而,该模型未能很好地捕捉到实验结果中的尖点区域。这是因为基于ONERA失速模型得到的结果在数学上是严格的二阶导数连续解,其无法模拟突跳的尖点等不可导区域。但从总体上来说,当引入ONERA失速模型后,失速后气动力的变化趋势和变化现象都能够被比较清晰地捕捉到。

3.2 考虑亚松弛迭代的静气弹问题研究

对于非线性颤振问题,无论是在频域内进行特征根轨迹分析,还是在时域内进行推进求解,首先应得到系统在某一条件下的初始稳态解,即静气弹求解问题。本小节通过一个算例,对比采用不同迭代方法得到的静气弹结果,以说明亚松弛迭代在静气弹求解中的意义,并采用亚松弛迭代法,给出不同初始攻角下,系统的静气弹解随来流速度的变化曲线。

对于图1的气动弹性系统式(9)给出了系统的状态空间形式。为了得到系统的静气动弹性控制方程,只需要将所有关于时间的导数项全部置零,最终得到系统的静气动弹性控制方程如下[14]:

(K-A3)·δ=F2Γ+C0

D2Γ+D0=0

(10)

式中,K为刚度阵,C0为零攻角气动力系数矩阵,δ为广义位移向量,Γ为失速气动力向量。需要注意的是,矩阵D0和D2是关于广义位移向量δ的复杂分段函数。如果在(10)式的第二式中直接将Γ解出,并带入第一式中去求解δ,算式将非常复杂。故本文采用迭代方法对两式进行依次间接求解。

以文献[8]中的算例为例,如图3所示展示出静态气动力系数随攻角变化曲线。

图3 静态气动力系数曲线

由图3可知,翼型的静失速攻角为13°。静态升力和力矩系数曲线的斜率在此处都有突变。图 4展示出采用简单迭代法和亚松弛迭代法得到的结果,其中亚松弛因子取0.4,翼型的初始攻角为18°,图中虚线代表了失速攻角的位置。

电力电缆设备故障的类型比较多，在当前技术应用中需要做好具体技术分析工作，结合系统本身流程要求和探测要求等，在故障分析的过程中采用循序渐进的方式进行处理。最重要的是强化系统日常维护处理，保证电力电缆设备发挥稳定性，为行业进步奠定基础。

图4 静气弹收敛历程对比图

当采用简单迭代法,静气动弹性解在来流速度为14.5 m/s和15.0 m/s时,均有不同程度的振荡。这是由于当来流速度为14.5 m/s和15.0 m/s时,解在静失速攻角附近反复迭代。而一旦涉及非线性迭代,差值过大将导致迭代过程的不稳定。当采用亚松弛迭代法时,系统解的稳定性提高,收敛曲线变得光滑。在来流速度为14.5 m/s和15.0 m/s时,解收敛到一个稳定值。然而,当来流速度为14.0 m/s时可以看出,当采用简单迭代法时,解在第三步已经收敛;当采用亚松弛迭代法时,解在第十步才基本收敛。采用亚松弛迭代法固然可以提高系统解的稳定性,但同时也会降低系统解的收敛速度,需要权衡考虑。

采用亚松弛迭代技术,通过数值模拟预测在不同初始攻角下,系统静气弹解随来流速度的变化情况,亚松弛因子取0.4。如图5所示展示出计算结果,其中点划线代表了失速攻角的位置:

图5 系统静气弹解变化曲线

由图5可知,当初始攻角一定时,来流速度越大,气动载荷越大,系统的静气弹解数值的绝对值也就越大;在来流速度一定时,初始攻角越大,曲线的斜率越大,表明静气弹解的发散速度越快。值得注意的是:每条曲线在13°处的斜率都是不连续的,斜率有明显下降。这是因为:当俯仰位移小于静失速攻角时,系统中的气动力只有线性气动力的参与;当俯仰位移大于静失速攻角时,非线性气动力将参与迭代过程,这将导致曲线斜率的突变。由于非线性气动力的参与,当攻角增加时,气动力增加趋势有所减缓,从而减缓了系统静气弹解的发散趋势。

3.3 失速颤振的颤振临界特性研究

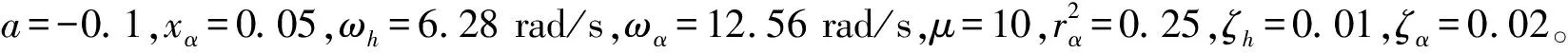
图6给出了系统在初始攻角为0°时的频域响应结果。其中a分支代表俯仰模态;b分支代表沉浮模态;c分支代表线性气动力项;d分支代表尾涡脱落项;e分支代表了非线性气动力项。

由图6a)中的根轨迹图可知,随着来流速度的增加,系统的俯仰模态分支a穿过虚轴,而A点对应的来流速度为16.9 m/s。此时系统由于俯仰模态失稳而发生颤振。从图6b)可以看出,在颤振临界点附近区域,系统的沉浮模态和俯仰模态频率在不断靠近,具有典型的经典颤振特性。此外,线性气动力c在B点的失稳代表着系统的静气动弹性发散,对应的来流速度为22.9 m/s,即系统静气弹发散速度为22.9 m/s。

下面研究大攻角下的系统响应。如图7～9所示,展示了初始攻角为25°,32°和35°时的系统频域响应结果。从图7～9可以看出,在大攻角情况下,系统颤振特性和经典颤振特性是不相同的。

图6 初始攻角为0°系统频域响应结果图7 初始攻角为25°系统频域响应结果

图8 初始攻角为32°系统频域响应结果图9 初始攻角为35°系统频域响应结果

当翼型的初始攻角为25°时,由图7a)的根轨迹图可知,在颤振边界附近,系统的非线性气动力模态分支e有失稳的趋势,系统的俯仰模态分支a穿过虚轴失稳。从图7b)可以看出,在颤振临界点附近,系统的俯仰模态分支a和非线性气动力模态分支e频率在不断靠近,表明系统的俯仰模态和非线性气动力模态有耦合的趋势。

当翼型的初始攻角为32°时,由图8a)的根轨迹图可知,随着气动力非线性的增强,系统的俯仰模态分支a和沉浮模态分支b相互吸引,根轨迹有相互靠近的趋势,但此时系统依然发生的是由于俯仰模态失稳主导的失速颤振。

当翼型的初始攻角为35°时,由图9a)的根轨迹图可知,系统的俯仰模态分支a和沉浮模态分支b继续相互吸引靠近,最终发生模态分支交换。此时系统从俯仰模态失稳转变为沉浮模态失稳。由图9b)可以看出, 在颤振临界点附近,系统的沉浮模态分支b和非线性气动力模态分支e频率在不断靠近,这表明系统的沉浮模态和非线性气动力模态有耦合的趋势。

综上所述,在翼型大攻角的失速颤振问题中,非线性气动力模态与结构模态的耦合作用可能导致结构模态失稳,从而诱发系统的单自由度颤振。

3.4 失速颤振的极限环振荡和分岔现象研究

本小节依然采用3.3小节的结构参数,进行失速颤振的极限环振荡和分岔现象的研究。图10给出了系统在初始攻角为14°,来流速度为10.1 m/s和10.7 m/s时的时域响应结果。

图10 不同来流速度下的系统响应

对于经典颤振问题,当来流速度超过颤振临界速度时,系统响应幅值为无限大值,此时系统发生了动气弹发散现象。对于失速颤振问题,当来流速度超过颤振临界速度时,系统响应幅值为有限值,此时系统处于极限环振荡状态,如图10b)所示。极限环振荡是非线性系统的典型特性。当飞行器结构发生极限环振荡时,虽然不会导致飞机的直接解体和破坏,但会带来较为严重的飞机结构疲劳问题。

图11 不同初始攻角下的系统分岔曲线

图11展示了不同初始攻角下,系统俯仰模态幅值随来流速度变化的分岔曲线,其中取初始静气弹平衡位置为零位置。每条分岔曲线都以小振幅的颤振临界状态为起始端,动气弹发散状态为结束端。当翼型的初始攻角为6°时,俯仰模态振幅在来流速度超过颤振临界速度后急剧增大,出现超临界霍夫分岔,幅值范围较小;当初始攻角增加到8°和14°时,俯仰模态振幅在来流速度超过颤振临界速度后增速减缓,同时模态幅值范围变大;当初始攻角增加到18°时,俯仰模态振幅在来流速度超过颤振临界速度后有一个小的阶跃,此后模态幅值增速略有增加。当初始攻角增加到28°和30°时,俯仰模态振幅的变化趋势和小攻角时十分相似。

综上所述,初始攻角的改变会显著影响系统俯仰模态的振幅分岔曲线特性。

3.5 初始扰动对系统响应的影响研究

当考虑失速颤振时,气动弹性系统本身作为非线性系统,其响应会受到初始扰动的影响。为此,有必要研究初始扰动对气动弹性系统响应的影响。在本算例中,依然采用3.3小节的结构参数,通过改变初始扰动值得到系统的响应情况。在数值模拟时,取初始静气弹平衡位置为零位置,初始攻角为25°。如图12所示给出了系统在不同初始扰动下俯仰模态幅值随来流速度的变化曲线。其中图12a)为全局图,图12b)为图12a)中圆圈区域的局部放大图。

图12 不同初始速度扰动下的系统响应

在初始扰动为2×10-3时,系统受到的外界扰动较小,当来流速度在6.3 m/s到6.8 m/s范围内时,系统做小幅值的极限环振荡,而当来流速度在6.8 m/s到7.3 m/s范围内,系统响应是收敛的,模态幅值为0;当来流速度超过7.3 m/s时,模态幅值又迅速大幅度增加。当初始扰动为0.1,0.05和0.02时,系统受到的外界扰动有所增大,俯仰模态幅值曲线几乎是完全重合的。在来流速度为6.3～6.8 m/s范围内时,系统做小幅值的极限环振荡。而当来流速度在6.75 m/s附近时,模态幅值迅速大幅度增加,此后沿着光滑的曲线逐渐上升,系统响应继续持续着极限环振荡状态,并未出现收敛现象。

综上所述,当初始扰动在0.02到0.1范围时,系统对扰动变化的敏感度较弱;而当初始扰动在2×10-3到0.02之间时,系统对扰动的变化非常敏感。当系统的初始扰动变大时,系统原先稳定的状态可能被激发为极限环振荡状态。