基于单目视觉多视图平面点位置的最优估计

丁尚文，王纯贤

（1.合肥工业大学 宣城校区基础部，宣城 242000：2.合肥工业大学 宣城校区机械工程系，宣城 242000）

基于单目视觉多角度测量的平面点位置最优估计是机器视觉研究的经典问题，同时也是机器人定位[1-2]，航天器交会对接[3-5]等技术的重要研究内容。

该方法主要基于多视图利用图像点特征解算相机坐标系相对世界坐标系的位置与姿态。文献[6]利用三焦点张量方法实现对机器人运动位置与姿态估计。文献[7]提出基于多视图的移动机器人视觉位置与姿态轨迹跟踪方法。为了实现车辆的位姿估计，文献[8]提出面向三视图几何相关约束的的视觉辅助导航和惯性导航系统相融合的方法。文献[9]利用三视图几何相关约束条件实现对相机相对世界坐标系下的相对位姿估计。文献[10]基于双目视觉方法对航天器间的位姿测量展开研究。文献[11]采用双目视觉测量方法对未知的空间物体在相机坐标系下的位姿给出估计算法。

空间平面点的定位较多地利用相机标定技术获得空间目标在世界坐标系下的位置。具体方法是将投影矩阵分解成得到相机内参数和外参数（旋转矩阵和平移），利用相机标定方法确定出相机参数，然后利用投影点的图像坐标重建特征点在世界坐标系下的位置[12]。由于相机标定误差的影响，以及分解形式不唯一性尤其是内参数的求解不稳定性，从而导致不同视角下重建的特征点坐标不完全相等。针对空间点的位置估计问题，在此提出基于单目视觉多角度测量的平面点位置最优估计。

1 坐标系建立和基本方程

1.1 坐标系建立

相机成像模型由针孔成像原理得到，相机标定是指建立相机图像像素位置与现实世界特征点位置之间的对应关系，由已知特征点的图像坐标和世界坐标求解相机的模型参数。在此就相机参数标定涉及到的4个坐标系建立给予详细描述，坐标系之间的关系如图1所示。

图1 四个坐标系相关位置Fig.1 Relative position of four coordinate systems

1）图像坐标系（l，u，v），简称（l）系。 计算机内的图像由一系列排列有序的像素点组成，坐标原点位于图像左上角，水平向右为u轴正方向，垂直向下为轴正方向，图像坐标（u，v）表示像素点在图像中的行列位置，单位为像素。

2）成像坐标系（i，x，y），简称（i）系。 （i）系被称作图像的物理坐标系。原点位于成像平面的中心点，水平向右为x轴正方向，垂直向下为y轴正方向，坐标（x，y）表示像点在图像中的物理位置，单位为mm。

3）相机坐标系（c，x，y，z），简称（c）系。 将相机的光心设为坐标原点，相机的光轴为z坐标轴、x轴和y轴分别平行于成像坐标系的横、纵轴，z坐标轴正方向方向符合右手坐标系法则。

4）世界坐标系（w，X，Y，Z），简称（w）系。 选择物体上的某一点作为坐标原点，X，Y和Z坐标轴的选取符合右手坐标系法则。

1.2 符号和基本方程

P=[X，Y，Z ]T表示在（w）系下的三维坐标，对应投影点用p=[u，v ]T表示。它们的齐次坐标对应记为。由针孔成像模型[7]，可得到

式中：s为非零尺度因子；［R，t］为（c）系相对（w）系的旋转矩阵、平移向量；α，β分别为摄像机在u方向、v 方向上的有效焦距；（u0，v0）为摄像机的主点坐标；λ为倾斜因子。

通常，假设在（w）系下的平面方程设为Z=0，为避免标记混淆，在此用表示平面模型的点表示平面模板特征点对应的图像齐次坐标。记ri表示旋转矩阵的R第i列（i=1，2，3），根据式（1），可以得到平面点与投影点对应的投影矩阵[12]，即

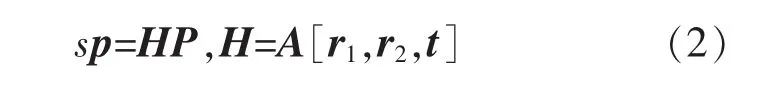
2 平面点最优估计模型与求解

利用式（2）将平面点与投影点对应的投影矩阵分解为

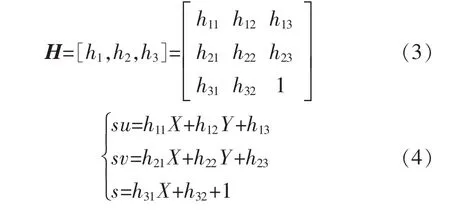
令 h′＝［h11h12h13h21h22h23h31h321］，则有

为了精确得到投影矩阵，建立基于像素坐标误差的目标函数，即

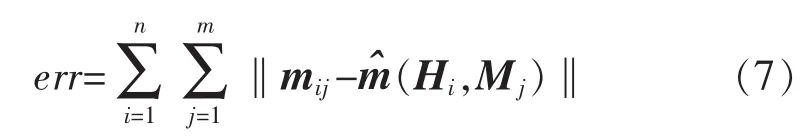
式中：mij为三维场景中第i个物点在第j幅图像上的图像坐标；Hi为第i幅图像与特征点之间的投影矩阵；Mj为平面上第 j个特征点空间坐标。中投影矩阵Hi的初始值可通过式（6）得到。采用非线性算法求解满足目标函数条件的最优值，即得到投影矩阵。利用投影矩阵，通过特征点的图像坐标，得到特征点在相机坐标系下的坐标，即

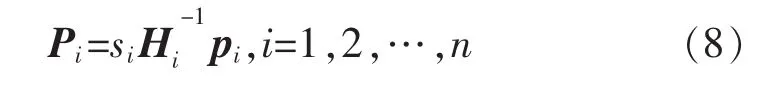
设 Pi点的坐标为，则Pi点的齐次坐标为

通过以上公式，可以发现不同的角度得到的单一矩阵不同，估计出来的特征点Pi点的横、纵坐标值存在着误差。假设特征点P在世界坐标系下的齐次坐标为，则其估计值应满足

对目标函数求偏导，即有下式成立：

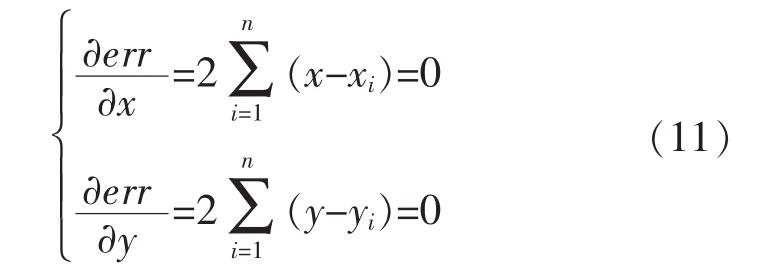
得到P点横、纵坐标的最优估计值为

利用式（12），可以得到空间平面内特征点P的位置。

3 试验测试

3.1 仿真试验验证

为了验证新线性算法有效性，文中使用了虚拟相机进行了仿真验证，并将本文试验结果与文献[12]的试验结果进行比较。

仿真试验参数如下：相机最大分辨率为2048×1536 像素；相机图像传感器大小为（6.4×4.8）mm2；相机内参数真值为f=8 mm；图像传感器中心在成像坐标系下的坐标为（Cx，Cy）=（3.3，2.5）；相机镜头水平和垂直方向上的畸变系数为k1=1，k2=1。平面图像特征点位置如图2所示。

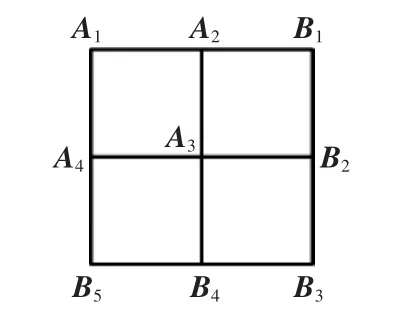
图2 仿真平面靶标位置Fig.2 Simulation plane target position

选取图2中至少4个特征点作为相机参数标定点[12]，例如：A1［0，0，0］，A2［10，0，0］，A3［10，10，0］，A4［0，10，0］。其余特征点位置分布在图2中所标注的位置。在此待验证的平面内特征点位置坐标分别为B1［20，0，0］，B2［20，10，0］，B3［20，20，0］，B4［10，20，0］，B5［0，20，0］。

虚拟相机从不同角度拍摄3幅图像。实际检测到成像点ai′的坐标受噪声影响存在误差，在此对获取到成像点 ai′的坐标（xai′，yai′）添加白噪声，白噪声从0增加到10个像素，步长为1像素。采用2种方法重建出的特征点坐标仿真如图3所示。

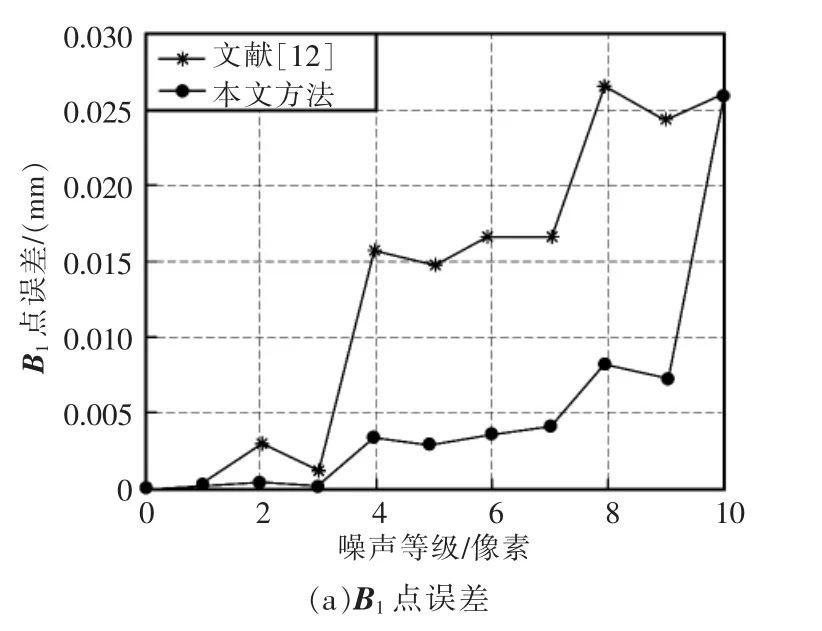
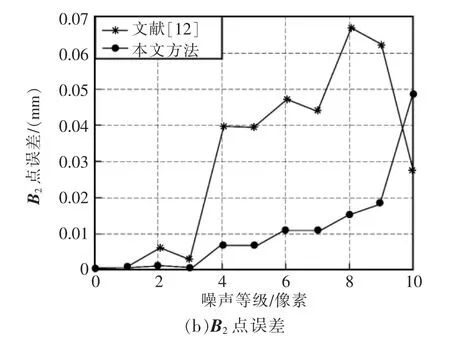
图3 特征点位置误差Fig.3 Feature points position error

由图3（a）可见，利用本文线性算法得到的特征点坐标的估计值与真实值误差平方和不超过0.025 mm；通过文献[12]方法得到的特征点坐标的估计值与真实值误差平方接近0.028 mm。

由图3（b）可见，利用本文线性算法得到的特征点坐标的估计值与真实值误差平方和估计值不超过0.05 mm；通过文献[12]方法得到的特征点坐标的估计值与真实值误差平方和接近0.07 mm。

3.2 位姿测量试验与分析

为了验证基于单目视觉多角度测量的平面点位置最优估计方法结果的可靠性和精度，在此对平面内特征点从不同视角拍摄3幅图像，试验中使用的平面模板如图4所示。

图4 平面模板图像特征点位置Fig.4 Feature point position of plane template image

相机参数如下：相机最大分辨率为像素；相机图像传感器大小为（6.4×4.8）mm2；相机焦距为 f=8 mm。

在图4中，左上区域内的4个特征点为解算投影矩阵的特征点，它们在（w）系下的坐标分别为A1［0，0，0］，A2［50，0，0］，A3［50，50，0］，A4［0，50，0］；随机选取的平面内4个特征点分布在图4中浅色所标注的位置上。待验证的平面内浅色的特征点位置坐标分别为 B1［60，60，0］，B2［80，80，0］，B3［100，100，0］，B4［120，120，0］。本文提出新方法所获得试验结果，与利用文献[12]方法获得试验结果进行比较，结果见表1。

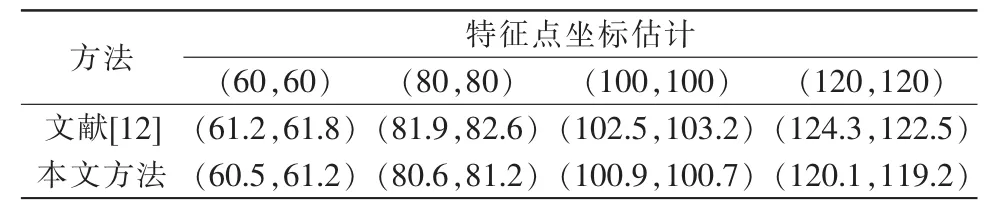
表1 两种方法重建点坐标估计Tab.1 Reconstruction of point coordinate estimation by two methods

由表可知，采用文献[12]方法获得特征点坐标（120，120）的误差为 4.3 mm；如果采用本文所提最优误差估计方法最大误差不超过0.8 mm，4个特征点坐标估计值误差最大不超过1.2 mm。可见，后者的特征点坐标估计精度高，能够有效降低不同视图下的随机误差的影响。

4 结语

空间平面点的定位较多的利用相机标定技术获得空间目标在世界坐标系下的位置。本文所提基于单目视觉多角度测量的平面点位置最优估计方法，利用投影矩阵，直接得到平面点的位置。采用本文的最优误差估计方法最大误差不超过1.2 mm，特征点坐标估计精度高，能够满足视觉测量的要求。后续的研究将着重于利用双目视觉测量三维点坐标以及最优点坐标估计问题。