Storm启发式均衡图划分调度优化方法

2018-11-14简琤峰张美玉

小型微型计算机系统 2018年11期

简琤峰,卢涛,张美玉

(浙江工业大学计算机学院数字媒体技术研究所,杭州 310023)

1 引言

面向移动互联网和大数据应用的实时数据流式处理技术[1,2]成为近年来相关研究领域的热点.Storm[3]提供了一种优秀的实时大数据流式计算模式得以广泛应用.但随着深入应用,其在资源和任务的调度策略上存在的问题也越来越突出:通信代价作为影响流式数据处理效率的重要因素,Storm调度器没有将其作为考虑因素;自带的均衡调度器会导致负载不均;并行度参数需要手动配置;无法根据集群运行状况对任务重调度等问题直接影响Storm集群的运行性能.

针对上述问题,文献[4]提出基于Topology结构的Offline调度器与基于Traffic的Online实时调度器,其中Offline调度器通过检测Topoloy结构一次性分配任务,而Online调度算法则实时检测负载与延时并应用了改进的贪心算法,优化Storm实时计算性能,实现动态调度;该文提出的算法仅考虑了通讯代价,而没有考虑到负载均衡.文献[5]设计了一个基于流量感知(Traffic aware)而优化调度的改进了整个Storm框架,事实上也是重点优化了通信代价这个维度,改进后的框架称之为T-Storm,相同任务下能够减少30%的服务延时.文献[6]借助Metis工具对任务的Topology进行多层K划分[7,8],自适应分层调度改进Storm.文献[9]通过感知本地资源的利用率以及网络延时来最大化Storm的吞吐量.文献[10]提出利用GPU来提升Storm计算能力的方法.在国内,阿里云对Storm进行的优化,称之为JStorm;其在网络IO、线程模型、资源调度、可用性及稳定性上做了持续改进,已被越来越多企业使用.

但是已有文献的优化中尚存在一些问题,如文献[4]使用贪心策略减小通信代价容易导致局部最优;文献[5]的基于流量感知(Traffic aware)的调度优化策略,仅优化了通信代价这个维度;文献[6]采用的图分方式相比于前面的方式有更好的全局优势,但图分时没有考虑顶点权重,负载均衡上存在问题.

本文首先为Storm建立调度模型,将Topology归结于带权图,以减小通信代价并保证负载均衡为目标,提出基于启发式均衡图划分算法的调度策略;以负载检测数据作为调度器的输入,实现动态调度、动态并行参数优化和重调度优化;通过Topology结构分析实现静态任务分配.最终减少集群节点间的数据发送率,并且保持节点间负载均衡;实现减少数据处理延时,提升集群吞吐量,优化整体性能的目标.

2 问题与建模

2.1 问题

1)不考虑通信代价

Storm的EvenScheduler的调度策略没有考虑通信代价.通过一个简单的实验来分析通信代价对集群性能的影响.实验环境参阅第四部分说明.实验使用Throughput Test topology,它是一个共有4个组件的链式Topology,用于吞吐量测试.实验测量一个消息元组Tuple从Spout出发到最后处理完成所花费的平均时延,在实验中为保证节点不会过载,因此将Spout的发送间隔时间设置为了5 ms,还设置的组件的并行度为1,即一个组件实例只有一个Executor负责,这样该Topology一共需要8个Executor(1 spout+3 bolt+4 ack个).观察和分析如下:

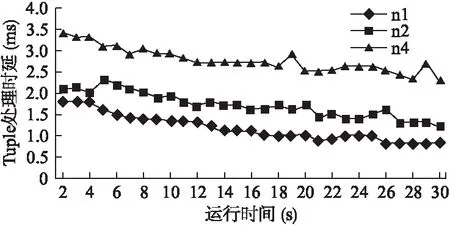
图1 通信代价对Tuple时延的影响

实验结果如图1,所有实验组都为Executor分配4个Worker,其中n1组表示这4个Worker分在同一节点,因此这些Worker之间没有网络间通信;n2组表示4个Worker被均分到2个节点,开始出现网络间通信;n4组表示4个Worker被均分到4个节点,网络间通信的代价进一步增大.从图中可以看出Tuple处理时延由n1至n4依次增大,在这个试验中n1与n4组由于增加的通信代价,Tuple处理时延增加了75%至近2.5倍.

2)负载不均

EvenScheduler中的排序策略的缺陷会导致任务分配失衡,这个均衡策略对于单个Topology的组件是均衡分配的,但无法保证每个节点的计算负载相对均衡.

3)参数配置难

在实际Topology t提交时,有两个需要手动设置的参数Worker并行度NUMw(t)和组件并行度NUMe(t).其中NUMe(t)的值则由公式(2)根据每个组件的并行度设置得到.

由于不清楚具体Topology的资源占用,在Topology应用开发时无法知道这些参数的最优配置.因此开发者在开发完Topology时需要手动监视运行时负载情况,然后根据经验调整.此外一些应用的负载跟用户访问有关,这些配置可能需要随时改变.

4)无法根据运行情况调整分配

Storm的调度器都是静态的分配任务,没有办法根据集群的运行状态动态调度.在集群运行时,Storm默认的调度器的作用除了为新提交的Topology,就是对异常挂起的Worker而被搁置的Task重新分配Worker.我们还需要在集群运行过程中根据负载情况实现实时调整分配.

2.2 优化目标

针对上述问题,本文提出以最小化通信代价为前提,尽量保持负载均衡的优化目标,以此来改进Storm集群的运行效率,提高整体性能.并且通过对集群节点的性能检测,可以随时重调度以调整分配结构,同时根据性能数据还可以调整Topology中的并行度参数,实现Topology结构的并行优化.

2.3 调度模型及优化方案

为达成上述优化目标,首先需要确立Storm的调度模型.Storm集群为主从结构,集群上运行的应用是Topology.如图2所示,Topology结构为一个有向无环图,箭头为数据传递方向.

图2 Topology结构示例

对于一个含有m个工作节点Storm集群N={nx|x∈[1,m]},每个节点nx配置有Sx个Slot,那么集群的计算资源即Slot集合R表示为:R={sxy=|x∈[1,k],y∈[1,Sx]},sxy为节点nx的第y个Slot.集群中一共有NUMr(N)个Slot资源:

(1)

对于即将提交至集群的Topologyt,若组件数量为NUMc(t),第i个组件ci的并行度参数记作PARALL(ci).即运行的Task数量,为了简单起见,本文约定一个Executer执行一个Task.在这种情况下,t的实例Task数量等于其所需的Executer数量,为:

(2)

对于t而言,若它的Worker并行度参数配置为NUMw(t),那么资源调度要做的就是:对于t的NUMt(t)个Task实例均分配给NUMw(t)个Worker,并将Worker分配到相应节点的相应Slot.这样,对t的资源调度可以表示为:

f(E)→W,g(W)→R

(3)

其中,函数f表示Executor到Worker的映射,函数g表示Worker到Slot的映射.上述E、W分别表示执行Task的Executor集合和容纳Executor的Worker集合.一次资源调度需要满足以下要求:1)t占用的Worker数应该小于等于集群的Slot数量;2)而对于函数f来说,t的Executer一般均匀地分配到Worker;3)当前研究版本(即0.9.0)的Storm不允许两个不是同一个Topology的Executor被分配到同一个Worker.

为优化该调度过程,需要建立性能采集器,并实现一个动态调度器以根据运行情况实时调度.Topology在Storm集群运行过程中会产生一些运行状态数据,通过建立性能采集器,可以获取组件的Executor之间在单位时间发送的Tuple数量、Executor线程的CPU时间.

其中性能检测采集器[4]设计如图3所示,Worker是运行Topology的工作进程,Executor是执行Task的线程.通过在每个Worker进程中注册一个性能监视线程,就可以检测这些Worker中各Executor工作负载及Tuple转发量.

图3 负载检测模型

Topology在附加了运行时的检测数据后,得到如图4所示的t的拓扑结构.其中椭圆表示一个Topology组件,小圆表示运行组件实例Task,小圆内数字则是计算代价(Executor线程的CPU时间),小圆的角标“[]”是其顶点ID;有向箭头是数据流向,而箭头上的数字则表示通信代价(Executor之间在单位时间发送的Tuple数量).假设NUMw(t)=k,表示根据配置t分到了k个Worker.

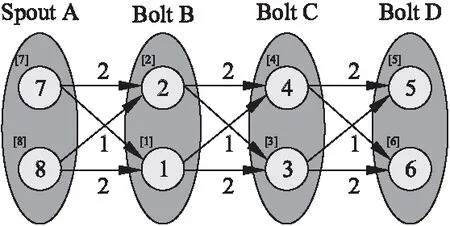
图4 一个链式Topology

我们将计算代价视作有向图的顶点权重,通信代价视作有向图的边权,那么调度问题可以视作一个图均衡划分问题,而动态体现在这张图需要随着性能检测数据的变化调整划分方式.由于有了性能数据,在动态调度器中还可以根据这些数据对Topology的并行度参数做一定的优化.

3 基于图划分的动态调度

3.1 启发式图划分算法

1)相关定义

上述方案指明了Topology的调度可以视作图划分.约定如下定义:

定义(3-1).带权图的最小化割权均衡k划分(本文中简称均衡图划分):给定一个带权图G=(V,E)和划分数k,k是正整数.其中V为图G的顶点集,E为其边集;代表了连接顶点u和顶点v的边,给定顶点u,ω(u)表示顶点u上的权值.同样,给定顶点u、v,ω(u,v)表示连接顶点u和v的边的权值.将V划分成k个不相交子集Vi,i=1…k,连接不同子集的边权之和最小化,且每个子集Vi中的子集点权满足:

(4)

ω(Vi)=ωe+α

(5)

其中上述的ωe即顶点子集权重的期望值,因此α越小,表示划分得越均衡.

定义(3-2).将带权图划分后,连接两个不同子集的边权之和称为割权.

2)均衡划分算法

针对上述提出的调度模型,本节提出了启发式算法K-PART来寻找带权的划分.根据优化目标,要求划分后各分组计算量差异最小,且最小化通信代价.因此所提算法K-PART划分策略是保证子集点权近似均衡的条件下,采用最大化子集内边权的策略[11]来最小化子集间的割权.假设要构建的k个子集分别是V1…Vk,算法首先将所有顶点移动到Vk中,同时计算子集点权的期望值ωe;然后逐个构建k-1个子集.构建子集Vi,i=1…k-1时,每次从Vk中取出使Vi子集边权增益最大的顶点v,放入Vi,直到Vi的子集点权到达条件.

构建子集Vi流程如下:输入参数是图G(V,E),k为划分数.首先是初始化计算,根据参数计算顶点子集点权的期望值ωe,初始化一个空的子集Vi,并且将图G所有的顶点都放在子集Vk中.然后开始为Vi分配顶点,为保证结果多样性,先随机从Vk中选择一个顶点vi到Vi;此时vi∈Vi,在Vk中与vi有邻接关系的点都被加入候选顶点的集合S,从S中选择一个vj,使得Vi子集边权增益最大,同时Vk中所有vj的邻接顶点被加入到S中.然后接着从S中取下一个使Vi子集边权增益最大顶点,直到满足条件ωe+α.到子集V1…Vk-1建立完成后,Vk中剩余顶点都属于Vk.其中顶点vj带给Vi的子集边权的增益是指,顶点vj从候选集S移动到Vi后,与移动之前所有属于Vi的顶点的边权和之差,即:

gain(v)=∑u∈Viω(u,v)-∑u∈Vkω(u,v)

(6)

算法形式化描述如下:

Input:G(V,E)、k

Output:Result={V1,…,Vk}

1 Start:

3 FOR(i=1;i<=k-1;i++)

4 S=ø,Vi=ø,v=null;

5 WHILE (ω(Vi)<=ωe)

6 IF(Vi==ø)

7 v=random(Vk);

8 ELSE

9 v=MAX(gain(u),u∈S);

10 ENDIF

11 Vi+=v,Vk-=v;

12 S+=Neighbor(v,u,u∈Vk);

13 END WHILE

14 Result+= Vi;

15 ENDFOR

16 END

3)平衡性调整策略

使用K-PART调度之后还是会带来分配不均的问题,还是由划分策略导致的.因为图是按照顶点来划分的,特别是在顶点数和划分数的比值接近1的时候(当然我们不考虑小于1的情况,这样没有意义),由于挑选的时候仅按照子集边权增益选取,并且每个子集都会在大于期望值时停止,当划分Vk-1时候选集已没有可分顶点了或者没有剩余顶点给Vk,亦或者Vk的子集点权远小于期望值.

因此本文再提出一个K-PART之后的平衡性调整策略,基本思想是:在最大子集点权的子集(作为候选集)中,选择一个使那个最小子集点权的子集的边权增益最大的点,移动到最小子集点权的子集中.迭代次数为图的顶点数量的倍数,称之为迭代倍率.这里用倍率来计算迭代次数,是为了期望每个点在单位迭代倍率下都有可能被遍历到.此外,当最大子集点权的子集仅包含一个元素时,则将次大子集点权的集合作为候选集.

定义(3-3)迭代倍率:在本文的平衡性调整策略中,迭代倍率就是被划分图顶点数量的倍数.

具体流程如下:K-PART的划分结果Result和迭代倍率Mul作为平衡性调整策略的参数.将Result={V1,…,Vk}结果集中的元素按照子集点权从小到大排序,那么Vmax=Result[k-1],Vmin=Result[0];它们分别对应公式(4-5)中的Vk和Vi,取Vmax中元素代入公式,找出一个使增益最大的顶点v,将v移动到Vmin,完成一次迭代;当Vmax中仅一个元素,则将次大集赋给Vmax.重复上述操作直到迭代NUM(V)*Mul次.

算法形式化描述如下:

Input:Result={V1,…,Vk}、Mul

Output:Result={V1,…,Vk}

1 Start:

2 FOR(i=0;i<=Mul*NUM(V);i++)

3 Result=sort(Result);//sort by ∑v∈Viω(v)

4 Vmax=Result[k-1];

5 Vmin=Result[0],idx=Result.size();

6 WHILE(Vmax.size==1&&idx--!=1)

7 Vmax=Result[idx];

8 ENDWHILE

9 v=MAX(gain(u),u∈Vmax);

10 Vmin+=v,Vmax-=v;

11 ENDFOR

12 END

当然,这个策略也会影响划分在通信代价上的优化,需要有一定的权衡.参阅第四章的实验.

3.2 仿真实验

1)实验条件描述

实验中采用随机带权图,给定数量的定点数与边数,它们的边随机与顶点关联,边权和顶点权重都被随机设置为1～100的整数.并且以如下指标来评价结果的优劣:

①割权比:衡量通信代价的优化程度,割权比是割权与图的总边权之比,值越小表示通信代价越小.割权比计算如下

cutRate:

(7)

②标准差与最大偏差率

这两个指标用户衡量划分均衡度.这里的标准差特指图划分子集后,将每个子集的子集点权作为统计样本计算得到的标准差.而这个最大偏差率则用来评价某些个体相比于期望负载的最大偏差,最大偏差率计算方式如下:

(8)

2)自身对比实验

自身对比实验用于测试迭代倍率对K-PART算法对划分效果的影响.自身对比实验的基本流程如下:1)随机生成带权图10张;2)每张图在不同迭代倍率的情况下分别做10次划分对比;3)整理实验结果,统计计算每次实验的各个指标.实验中随机生成的10张图都为G(24,36);划分数固定为k=3,迭代次数Mul从0增长到9倍,其中0表示不进行迭代.实验结果如图5所示.

从图5(a)的结果反映了随着迭代倍率增加,割权比会有少量的增加;从图5(b)和图5(c)的结果看出,随着迭代倍率的增加,子集点权的标准差和最大偏差率都有大幅度减小.

3)对照组实验

对照组实验用于比对本文算法与其他调度策略在输入不同复杂度的带权图及不同划分数的情况下的分配效果.比较对象是:1)K-PART:本文算法;2)T-PART:文献[4]基于Traffic的OnlineScheduler中的划分算法;3)M-PART:文献[6]基于Metis的P-Scheduler;

为了方便对比,本文统一重新实现对照组调度器的算法,并且输入相同格式的Topology图数据进行实验.

图5 迭代倍率对划分效果的影响

实验1.流程如下:1)随机生成10张带权图,划分数k逐渐增加;2)分别使用上述算法进行调度,每个算法都会对每张图作10次划分;3)对调度结果进行评估统计,计算每组指标的平均值.实验中图都为G(24,36),划分数k从2增加到24,平衡性调整的迭代次数Mul=0或者Mul=5.实验结果如图6所示.

从图6的实验结果可以看出,当划分数从2开始增加到接近总的顶点数时,各个算法的割权比和最大偏差率都会有上升趋势,权重标准差相对稳定(除了M-PART),这意味着划分的通信代价优化和均衡度都会变差.在划分数为顶点数的1/2及以下时,K-PART(Mul=0)的划分效果都是比较优秀的;K-PART(Mul=5)和T-PART次之,而M-PART也不错,但其结果非常不稳定.当划分数比顶点数趋向于1时,K-PART(Mul=5)的割权比也趋向于1.这是因为这里图划分算法是按顶点为单位开始划分的,因此在划分数比顶点数趋向于1时,由于K-PART平衡性调整策略的作用,使得每个子集仅包含1个元素,因此割权等于总边权.K-PART(Mul=0)和T-PART以减少割权比优先,因此在达到一定程度时优先保证了割权比;M-PART似乎走了减少割权比的极端,割权比占优的M-PART在均衡度上将会大打折扣,分析发现其产生大量空集.

实验2.流程如下:1)随机生成10组固定顶点数,边数依

图6 划分数对划分效果影响

次增加的带权图,每组10张图;2)分别使用上述算法进行调度划分,每个算法都会对每张图作10次划分;3)对调度结果进行评估统计,计算每组指标的平均值.实验中带权图顶点数固定12,边数从15开始增加,步进3;每个边数的小组各10张图,划分数k固定为3,平衡性调整的迭代次数Mul=0或者Mul=5.实验结果如图7所示.

图7 图连接复杂度对划分效果的影响

由图7的实验结果可以看出,图的连接复杂度并没有明显影响算法对划分结果中的割权比、标准差与最大偏差率指标.同时上述10组实验中,本文算法K-PART在平衡性调整迭代倍率Mul=0的实验组的划分割权比一直是最小的,因此它对通信代价的优化程度在这几组中是最好的;在平衡性调整迭代倍率Mul=5的实验组中,划分的均衡度一直是最优的.

4)实验结论

①在所对比的试验中,本文算法的划分效果优于对比算法;其中Mul>0时,在均衡度上占优,Mul=0则在割权比上占优;②所有对比的算法中,划分数与顶点数的比值越小,划分效果越好;③对于本文算法,平衡性调正策略迭代次数越多,分配越趋于均衡;但是会损失一些割权比上的优化.

3.3 动态调度策略

1)调度策略

根据前文对调度的定义,它包含f(E)→W和g(W)→R两步.在满足调度必要性的条件判断之后开始执行调度.第一步f(E)→W的本质上是根据t的配置生成E、W,利用前文提出的K-PART算法将E均匀划分,分配到W中.第二步g(W)→R则需要完成将第一步中得到的Worker总集合W按照设定目标分配到物理节点集N.

最后在调度生效之前,还需做进一步调整.算法遍历各节点的Worker,如果在同一个节点存在多个同一Topology的Worker,还可对其Executor执行一次均分.满足调度必要规则条件时生效这次调度.

调度生效的必要规则如下:在调度之前,调度器根据性能监测数据计算节点间Tuple发送率和均衡度指标;调度器计算新的分配方案之后,利用旧的性能监测数据估算这两个性能指标,当估算值都优于原指标时,开始实施重调度.算法形式化描述如下:

2)动态并行参数优化

Storm的并行度参数主要有三个:Worker并行度参数和Executor并行度参数以及Task并行度参数,后两者的乘积为组件的并行度;由于本文只考虑一个Executor只运行一个Task的情况,则Executor并行度等于组件的并行度.Worker并行度参数表示为一个Topology分配的Worker数量,对于这个参数,只要在资源允许的条件下是越大越好的.同一个Topology的不同组件的并行度参数就不能像上述Worker并行度参数那样设置了.

本文实现的动态调度器中,对于组件的并行度参数优化策略如下:

①输入:Executor负载数据,Topology结构t;

②分组计算:对Executor按照所属组件分组求和,得到组件的CPU计算量L;

③求比:对于属于t的任意组件ci和组件cj,如果数据由ci向cj传递,且L(ci):L(cj)=a:b,则PARALL(ci):PARALL(cj)=a:b;

④整合优化:整合组件间并行化参数比,将并行化参数之和等比扩大到Worker进程的线程数推荐值(10～15,该值是Storm开源软件作者Nathan给出);

⑤生效:遍历t的组件,修改其并行度参数.

3)重调度优化

动态调度策略根据当前的性能数据计算出新的分配方案后,面临一个Worker重新分配部署的问题.重新部署时需要先将相应Worker关闭,在新的节点的相应Slot重新开启.这是一个相对消耗资源的过程,并且会带来服务中断.因此在实施重调度优化的目标是:减少重调度对计算服务的影响,实现平滑的重新分配.

本文提出的重调度优化的基本思想是减少Worker迁移数,在迁移数不能减少的情况下优先移动计算量小的Worker,并且对Worker分批迁移.

具体流程如下:

①输入:以集群当前分配表Acur与动态调度策略得到的新分配表Anew为输入;

②待重调度集Sreassign:Acur中的每个Worker遍历比较Anew中Worker的Task分配,Acur中Worker的Task发生变化的Worker移动到待重调度集Sreassign;

③待重调度集Sreassign:Acur中的Worker按照Node分组,并按照Worker数量对Node分组由大到小排序;每次取出第一组,如果该组中的Worker在Anew中位于同一个Part,则不操作继续取下一组;否则取出改组中计算量最小的Worker放入Sreassign,直到该组中的Worker都对应到Anew中的同一个Part;

④迁移Worker:首先从Sreassign中随机取出一个Worker记作当前迁移对象Q,根据Anew找到Q应当分配到的Acur中Node分组,如Q的Task与Acur中不一致则重新分配Task,然后关闭一个Node分组中一个属于Sreassign的Worker,并由Q替换且从Sreassign移除,分配完后将被关闭的Worker记作Q.直到为Sreassign空.

4 实验与分析

4.1 实验环境

实验在一个由安装ESXI6.0系统的Dell R710服务器上的虚拟化集群进行.服务器的基本配置如下:CPU:Intel(R)Xeon(R)X5650,2.67GHz×6 core×2;RAM:128GB;1Gbps×4的网卡以及2个1T硬盘组成的磁盘阵列.

虚拟节点的配置是:每个虚拟节点CPU为2.67GHz×4 core、RAM为4GB,并用1Gbps的网络连接;操作系统是Ubuntu 14.04 X86_64(Linux 4.2.0).集群布置如表1所示.

表1 Storm节点配置

为了记录Topology运行时数据,专门设计了一个Topology,该Topology基于Word Count Topology[12].该Topology一共有4个组件,Worker的默认配置数为8,组件的默认设为并行度为4.为方便实验,本文对其进行了以下改造:1)在该Topology的每个组件初始化方法中增加性能监视器的注册,每个处理方法中通信Tuple统计;2)为了采集Tuple处理时延和吞吐量,在Spout发送消息时增加发送时间戳字段,并在Storm的可靠性保障中的ACK接口实现中增加时间差计算和消息计数.另外,为保证时间相关的测量数据的准确性,集群所有节点配置了NTP时间同步协议来同步集群时间.

4.2 评价指标

本文用如下指标评价性能:1)Tuple处理时延,即指一个Tuple从Spout发出后,直到处理完全后Spout收到Ack信号所花费的时间,反映集群的响应效率,该指标越小越好；2)单位时间Tuple处理量,即每秒处理的Tuple个数,反映集群的吞吐量,该指标越大越好.

本文用均衡度与节点间Tuple转发率指标评价调度效果.均衡度是性能采集器采集的各节点的CPU计算量的标准差,节点间Tuple转发率的值等于通过网络发送Tuple数量和集群所有Tuple数量之比.这两个指标相当于图均衡划分中的标准差与割权比,调度效果的评价指标越好,越有利于实际性能指标的提升.

4.3 对比实验

实验中给出的指标数据由本文实现的性能监视器保存在性能数据库中的数据整理得到.比较对象是:

1)KPartScheduler:由本文算法实现的动态调度器;

2)OnlineScheduler:文献[8]基于Traffic的在线实时调度器;

3)EvenScheduler:Storm中自带的均衡调度器.

1)调度器指标

图8为集群运行时的节点间CPU计算量的标准差.由图可知,在当前给定实验环境下KPartScheduler和OnlineScheduler在均衡度方面相差不大,但是EvenScheduler在均衡度上要明显差于前两者.

图9为集群运行时的节点间Tuple发送率.由图可知,在当前给定实验环境下KPartScheduler在通信代价优化上要优于OnlineScheduler,EvenScheduler对通信代价的优化是最差的,分别比KPartScheduler、OnlineScheduler调度器差5、3个百分点.

2)性能指标对比

图10为集群运行时的Tuple处理时延.由图可知,在当前给定实验环境下,KPartScheduler调度器下的集群Tuple处理时延随着系统运行中的不断重调度,处理时延越来越小;OnlineScheduler在前期收敛速度快,迅速达到的较优状态,但是系统最终稳定时,KPartScheduler调度下的Tuple处理时延要低于OnlineScheduler.而EvenScheduler在分配Topology后一直保持相对稳定的运行状态,且最终在Tuple处理时延性能上被前两者超越.

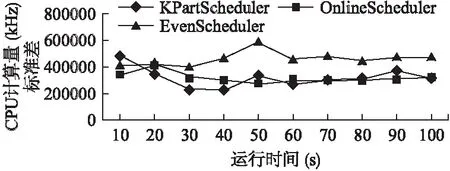
图8 集群节点间计算量标准差

图9 节点间Tuple发送率

图10 运行时Tuple处理时延

单位时间Tuple处理量就是集群吞吐量的反映.图11为集群运行时单位时间Tuple处理量.由Topology开始运行到运行状态趋于稳定,KPartScheduler和OnlineScheduler下的吞吐量相差不大,到后期KPartScheduler出现一定的优势.运行前期OnlineScheduler以最快的速度达到较优状态.