导数与函数的最大（小）值教学设计

沈蓉蓉

课型：新授课。

课时：2课时。

教具：多媒体。

教材：北师版选修2-2。

教学方法：启发、探究式教学。

教学模式：课堂互动教学。

教学目标：

（一）知识与技能

1.理解函数最值的概念、最值与极值的关系。

2.掌握求函数最值步骤。

3.通过建立函数模型，掌握用导数解决实际问题中的最优化问题。

（二）过程与方法

体会从特殊到一般的方法，培养学生观察、猜想、归纳、概括的能力。

（三）情感价值观

让学生在用导数处理问题时感悟数学方法，激发学生自主探究的精神。

教学重点：用导数求函数的最值。

教学难点：实际问题中的数学建模思想。

教学环节：

一、复习引入

1.判定极大、极小值的方法。

2.极大值一定大于极小值吗？

3.求极值的步骤。

师生互动：

师：提问学生。

生：回答问题。

设计意图：复习巩固，为本节课做铺垫。

二、问题探究

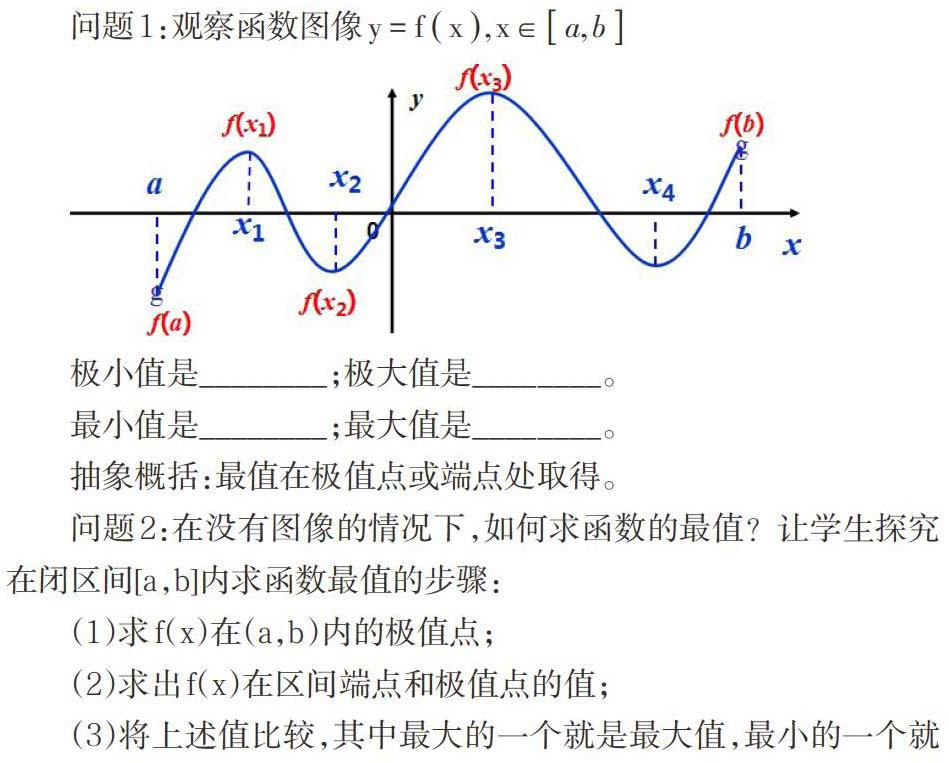
问题1：观察函数图像[y=fx，x∈a，b]

极小值是________；极大值是________。

最小值是________；最大值是________。

抽象概括：最值在极值点或端点处取得。

问题2：在没有图像的情况下，如何求函数的最值？让学生探究在闭区间[a，b]内求函数最值的步骤：

（1）求f（x）在（a，b）内的极值点；

（2）求出f（x）在区间端点和极值点的值；

（3）将上述值比较，其中最大的一个就是最大值，最小的一个就是最小值。

师生互动：

师：引导学生观察图像，提出问题。

生：回答问题。

师：PPT展示，引导学生总结规律。

设计意图：①由图直观地展示极值、最值的區别和联系；②由特殊到一般，从有图到没图，让学生分析、总结归纳求函数最值的步骤；提高自身抽象概括的能力。

三、实例分析，师生互动

活动1：课本66页例4。

生：小组讨论分析例4。

师：板书解题过程。

活动2：变式训练：将上面例题区间[-2，2]改成[1，4]。

生：板书解题过程。

活动3：课本67页例5（实际应用题）。

生：小组讨论写出解题过程。

师：投影仪展示学生答案。

设计意图：①通过例题让学生掌握利用导数求函数最值的步骤；②进一步加强对求最值步骤的掌握；③通过此题掌握最值在实际问题中的应用。

四、课堂练习，巩固新知

1.判断（正确的打“√”，错误的打“×”）。

（1）函数的最大值一定是函数的极大值。（ ）

（2）开区间上的单调连续函数无最值。（ ）

（3）函数f（x）在区间[a，b]上的最大值和最小值一定在两个端点处取得。（ ）

2.函数f（x）=2x-cos x在（-∞，+∞）上（ ）

A.无最值 B.有极值 C.有最大值 D.有最小值

3.已知函数f（x）=-x3+3x2+m（x∈[-2，2]），f（x）的最小值为1，则m=________。

师生互动：

生：自主完成。

师：叫部分学生回答。

设计意图：及时巩固所学内容，并加强提高。

五、课堂小结

1.极值、最值的区别与联系。

2.求函数最值的步骤。

六、课后作业

必做：课本69页习题3-2A组2、4题。

选做：已知函数f（x）=+2lnx，若当a>0时，f（x）≥2恒成立，如何求实数a的取值范围？