高超声速翼型气动特性设计与研究

，

(1.中国飞行试验研究院飞机所，陕西西安710089；2.中国飞行试验研究院航电所，陕西西安710089)

随着高超声速飞行器的高速发展及人类对地外空间探索活动的日益频繁，对于现代高超声速飞行器的设计，只保证高超声速状态下的气动性能，早已无法满足未来高超声速飞行器性能的需求。具有更宽速域的优良的气动特性已经成为高超声速飞行器发展的必然趋势[1-2]。这就要求高超声速飞行器需要从地面起飞，经历低速、跨声速、超声速阶段，直至高超声速巡航等多个飞行阶段都具有优良的气动性能。

国内外关于翼型的气动优化设计方面的工作[3-6]大多只考虑单一速域的气动特性，并没有兼顾低速以及跨、超和高超声速气动特性。而西北工业大学韩忠华教授、宋文萍教授团队利用自主开发的基于代理模型的多目标多约束高效通用优化程序“SurroOpt”[7-8]，设计了一种能够兼顾跨声速和高超声速气动特性的翼型并申请了一项专利[9-10]。该翼型在保证高超声速高升阻比的同时，跨声速特性也能得到满足，初步探索了高超声速翼型兼顾跨声速气动特性的可能。

本文基于RANS的CFD数值模拟方法，开展了高超声速翼型的气动特性设计与研究，设计了具有更加优良的低速、跨声速气动特性的高超声速翼型。

1 流动控制方程及设计方法

本文采用基于RANS的CFD数值模拟方法。其中CFD计算正确性验证在文献[9]中有详细介绍，本文不再赘述。

本文采用代理优化方法，优化设计流程如图1所示。其中翼型的参数化采用8阶直接CST参数化方法[11-12]。

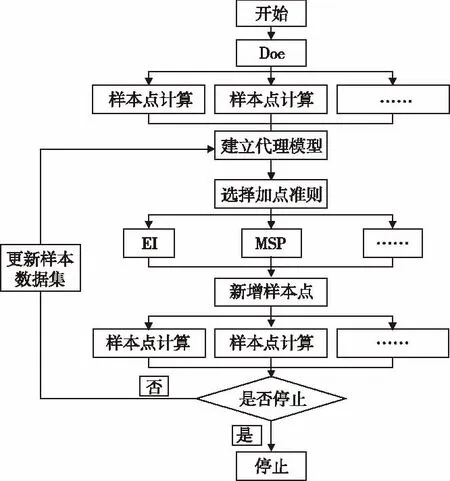
图1 代理优化方法流程图

2 高超声速翼型优化设计

文献[9]和[10]中设计了一种具有独特的下表面靠前缘处为反“S”型和下表面靠后缘处为“S”型特征的新翼型(NPU-Hyper-04)，能够兼顾跨声速和高超声速气动特性。为了再次提高翼型在低速、跨声速状态下的气动性能，以文献[9-10]NPU-Hyper-04翼型为基准翼型，分别以下列两个优化方案对其开展高超声速翼型优化设计研究：1)以翼型跨声速的最大升阻比为优化目标，以低速、超声速和高超声速状态下的升力系数和升阻比为气动约束进行优化设计；2)以翼型低速的最大升力系数为优化目标，以跨声速、超声速和高超声速状态下的升力系数和升阻比为气动约束进行优化设计。具体的设计工况为：

1)低速设计状态：H=0 km，Ma=0.2，Re=4.66×106，α=5°；

2)跨声速设计状态：H=9 km，Ma=0.8，Re=7.6×106，α=1.5°；

3)超声速设计状态：H=10 km，Ma=1.5，Re=1.28×107，α=4°；

4)高超声速设计状态：H=26 km，Ma=6，Re=4.23×106，α=5°。

优化方案一的数学模型表述为：

maxKl，Ma=0.8

s.t. (1)KMa=0.2>0.9×K0，Ma=0.2

(2)KMa=0.8>0.9×K0，Ma=0.8

(3)KMa=1.5>0.9×K0，Ma=1.5

(4)Cl，Ma=0.2>0.9×Cl0，Ma=0.2

(5)Cl，Ma=0.8>Cl0，Ma=0.8

(6)Cl，Ma=1.5>0.9×Cl0，Ma=1.5

(7)Cl，Ma=6>0.9×Cl0，Ma=6

(8)|t-t0|<0.02t0

优化方案二的数学模型表述为：

maxCl，Ma=0.2

s.t. (1)KMa=0.2>K0，Ma=0.2

(2)KMa=0.8>0.9×K0，Ma=0.8

(3)KMa=1.5>0.9×K0，Ma=1.5

(4)KMa=6>0.9×K0，Ma=6

(5)Cl，Ma=0.8>0.9×Cl0，Ma=0.8

(6)Cl，Ma=1.5>0.9×Cl0，Ma=1.5

(7)Cl，Ma=6>0.9×Cl0，Ma=6

(8)|t-t0|<0.02t0

其中，KMa=0.2、KMa=0.8、KMa=1.5和KMa=6分别为翼型在低速、跨声速、超声速和高超声速下的升阻比，Cl，Ma=0.2、Cl，Ma=0.8、Cl，Ma=1.5和Cl，Ma=6为翼型在低速、跨声速、超声速和高超声速下的升力系数，t为优化翼型的厚度。下标 “0”的为基准翼型的力系数和翼型厚度。

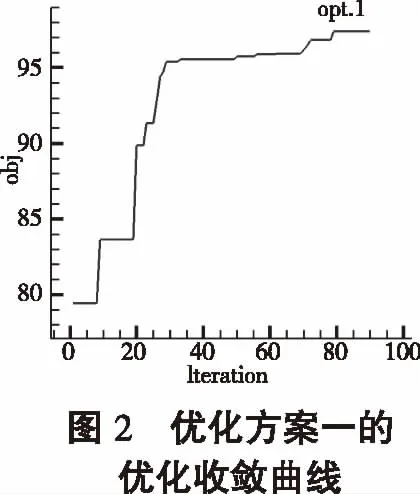
图2和图3为优化方案一和方案二的优化收敛曲线。可以看出两种优化问题都已收敛。图4为基准翼型与两种优化翼型的几何外形对比图。可以看出，两种优化翼型都保持了基准翼型的外形特征，相比于基准翼型，两种优化翼型前倒圆半径略微增大，前缘下表面弯度变小，后缘下表面弯度变大；其中，优化翼型二的前缘下表面弯度更小。

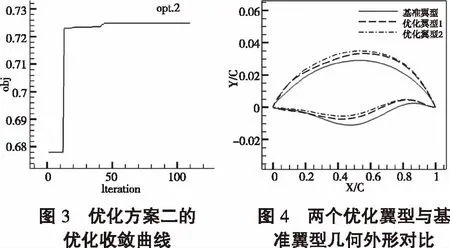
图5为基准翼型与两种优化翼型的压力系数分布对比图。图6至图9为基准翼型与两种优化翼型在亚、跨、超声速和高超声速状态下的压力云图对比。跨声速状态下，优化翼型一上表面的低压区更大，优化翼型二的上表面会产生双激波；由于两个优化翼型与基准翼型一致的外形特性，即双“S”型特征，因此在超声速和高超声速状态下的压力分布也基本一致，但是两个优化翼型后缘弯度的增大，在高超声速状态时，下表面压力增大，而前倒圆半径的增大，也导致了两种优化翼型超声速和高超声速前缘下表面压力的减小，以至于气动性能的降低。

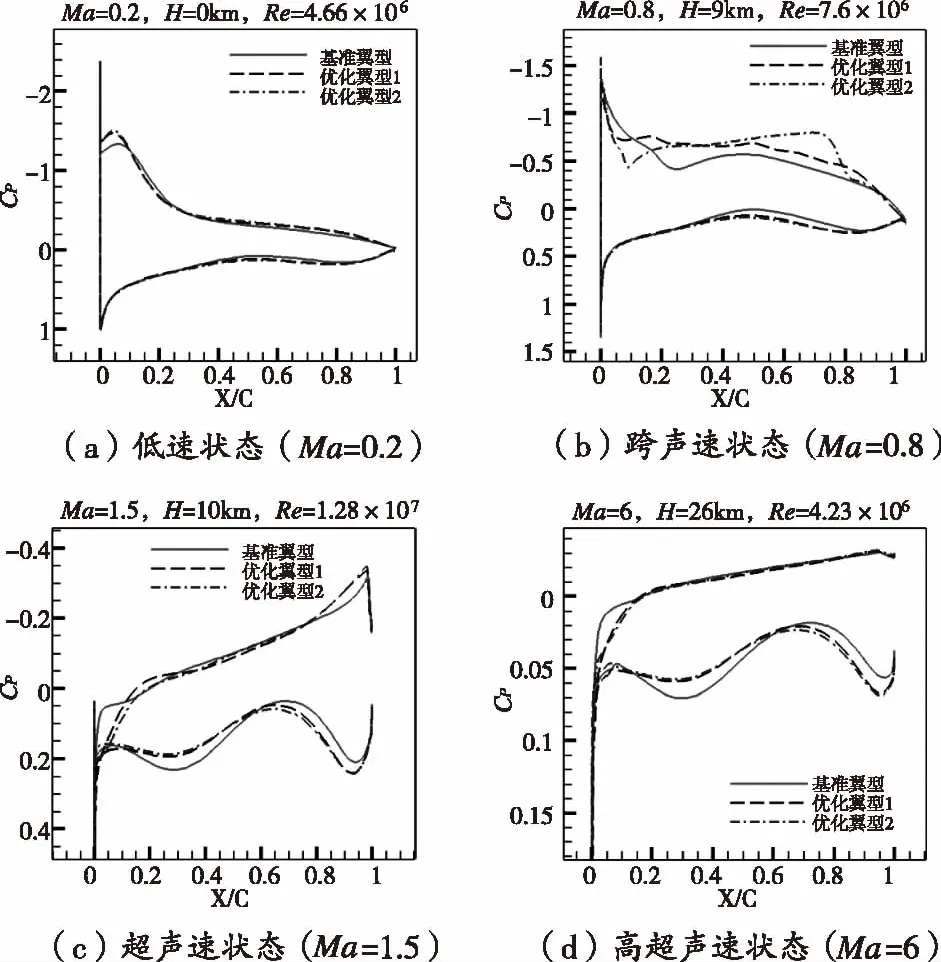
图5 两种优化翼型与基准翼型压力系数分布对比图

图6 低速计算状态下两种优化翼型与基准翼型压力云图 对比图(Ma=0.2，α=5°)

图7 跨声速计算状态下两种优化翼型与基准翼型压力云图对比图(Ma=0.8，α=1.5°)

图8 超声速计算状态下两种优化翼型与基准翼型压力云图对比图(Ma=1.5，α=4°)

图9 高超声速计算状态下两种优化翼型与基准翼型压力云图对比图(Ma=6，α=4°)

图10至图13分别为两个优化翼型与基准翼型在亚、跨、超声速和高超声速状态下的气动力特性对比。表 1和表 2为不同速域下两个优化翼型与基准翼型在计算攻角下的气动特性对比。可以明显看出两个优化翼型在亚、跨声速下的气动特性明显优于基准翼型，而在超、高超声速状态下，两个优化翼型的气动特性比基准翼型有所降低。低速状态下，两个优化翼型的升力系数均高于基准翼型，其中优化翼型二的升力系数更大，高出基准翼型8.19%；基准翼型与两个优化翼型的阻力系数相差不大；而两个优化翼型在低速状态的升阻比远大于基准翼型。跨声速状态下，两个优化翼型的升力系数也都高于基准翼型，三者的阻力系数基本相当；优化翼型一在跨声速状态的升阻比远优于基准翼型，计算状态下高出基准翼型23.45%。优化翼型一在跨声速时(Ma=0.8，α=1.5°)最大升阻比达到97.4018，优化翼型二在低速计算状态下(Ma=0.2，α=5°)的升力系数达到0.7187。以低马赫数为设计点的两个宽速域翼型，在亚、跨声速范围内表现出了良好的气动性能。

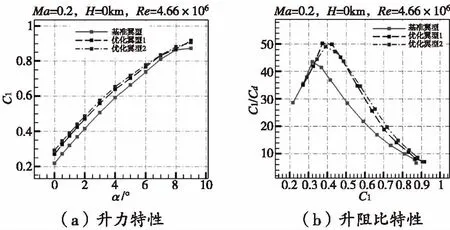
图10 低速状态下两种优化翼型与基准翼型的气动力 特性对比(Ma=0.2)

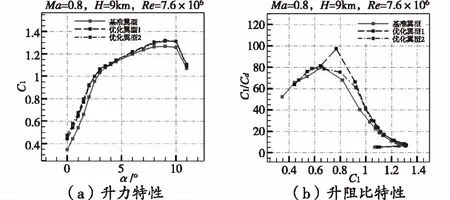
图11 跨声速状态下两种优化翼型与基准翼型的气动力 特性对比(Ma=0.8)

图12 超声速状态下两种优化翼型与基准翼型的气动力 特性对比(Ma=1.5)

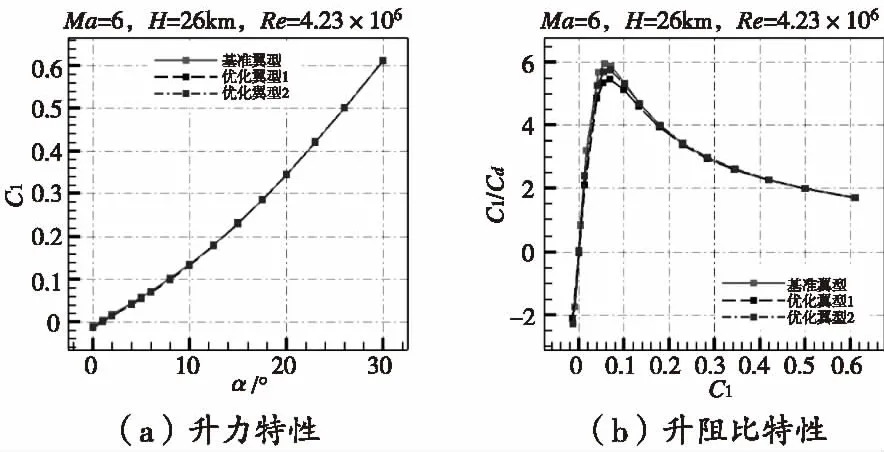
图13 高超声速状态下两种优化翼型与基准翼型的气 动力特性对比(Ma=6)

在超声速和高超声速状态下，基准翼型与两个优化翼型的升力系数和阻力系数相差不大。而在优化设计中，为了获得低速和跨声速状态下优良的气动特性，必然要牺牲部分超声速和高超声速的气动特性，所以两个优化翼型在超声速和高超声速计算状态下的升阻比略小于基准翼型，但是随着攻角的增大，三种翼型的升阻比相差不大。超声速计算状态下，优化翼型一的升阻比小于基准翼型9.47%，优化翼型二的升阻比小于基准翼型9.94%；超声速计算状态下，优化翼型一的升阻比小于基准翼型10.1%，优化翼型二的升阻比小于基准翼型4.13%。

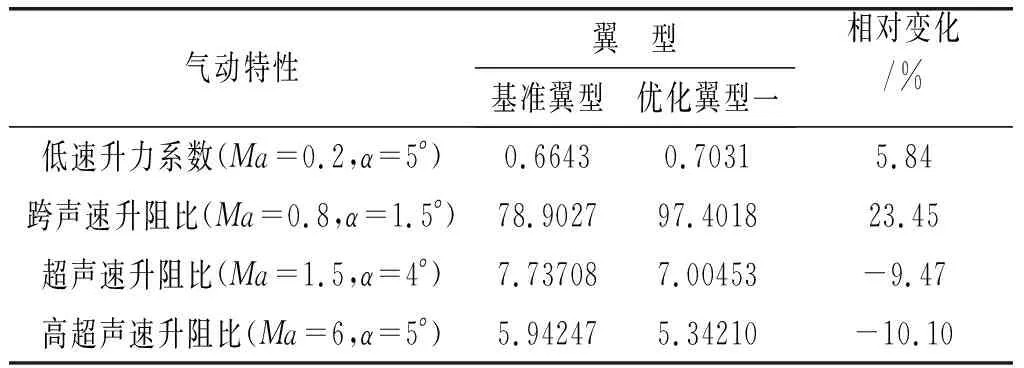
表1不同马赫数下优化翼型一与基准翼型气动特性对比

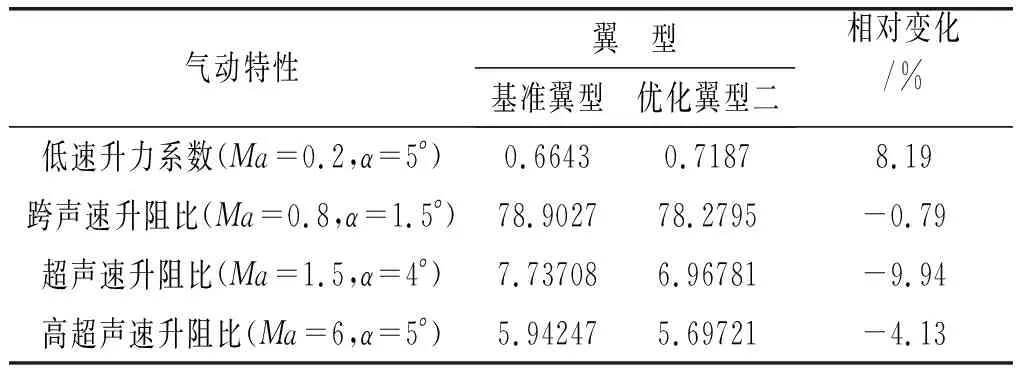
表2不同马赫数下优化翼型二和基准翼型气动特性对比

图14为典型状态下两个优化翼型与基准翼型的气动力系数随马赫数的变化对比图。可以看出，在亚、跨声速阶段，优化翼型二具有更大的升力系数，跨声速状态下优化翼型一具有更大的升阻比，两个优化翼型在亚跨声速气动特性得到明显提升；之后随着马赫数增大，基准翼型的升力系数和升阻比始终略高于两个优化翼型，但差距并不大。

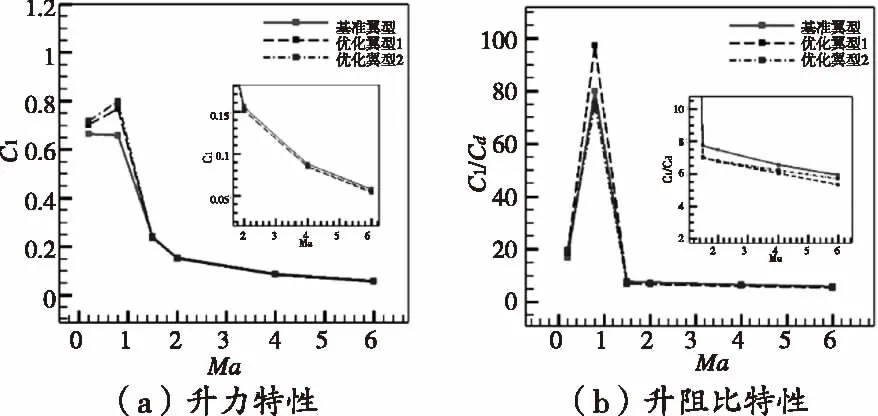
图14 两种优化翼型与基准翼型的气动力系数随马 赫数的变化对比

3 结论

本文开展了高超声速翼型气动特性设计研究，设计出了两种具有更加优良的低速、跨声速气动特性的高超声速翼型。通过对两种优化翼型进行综合对比分析，得出以下两点研究结论：

1)本文优化得到的两个翼型在亚、跨声速状态下的气动特性相较于基准翼型得到大幅度提升，在超声速、高超声速状态下的气动特性略有降低，但是差距并不大，实现了从低速到高超声速内整体气动性能的提高。

2)翼型在低速和高速下的气动特性是相互矛盾的，为了使设计者最关心的速域状态下的气动特性得到明显的提升，必然会损失一部分其他速度域的气动特性。