基于模糊数学理论的预制梁场规划建设及施工管理
2018-11-13梁允伟
梁允伟
(广西路建工程集团有限公司,广西 南宁 530001)
0 引言
随着我国经济的高速发展和综合国力的不断增强,国家对于基础设施的需求也与日俱增,其中,高速公路建设得到了空前的发展。在高速公路建设过程中,桥梁建设是必不可少的环节。在桥梁工程施工过程中,一般都是在预制梁场中制作预制梁,这是因为采用预制梁结构具有施工方便、施工效率高、施工周期短、便于现场管理等特点。同时,在预制梁场内制作的成品梁经过运输和吊装安放到设计位置上,其质量与生产进度直接影响整个工程质量与工期进度[1]。因此,在桥梁的施工期,对于预制梁场的选址以及设计都是极其重要的。针对预制梁场的选址与设计内容包括两个方面:预制梁场的宏观选址与细观设计。本文基于模糊数学的相关方法与应用,利用多属性模糊决策理论对预制梁场场内布置方案进行评价,建立模糊多属性决策模型进行计算分析,并验证其是否与项目实际相符合。
1 预制梁场选址的基本原则与影响因素
1.1 预制梁场选址的基本原则
通常,在主体工程的施工过程中,虽然预制梁场是作为附属工地,但是其选址的好坏影响着整个工程的工期进度以及施工成本。因此,通过对国内外工程实例的预制场选址分析,总结预制梁场选择位置时须遵守的原则:
(1)预制梁的生产与桥梁主体工程的施工之间不能相互干扰、相互影响。
(2)应在施工区范围内或者施工区附近选择合适的场地作为预制梁场。
(3)预制梁的制作受制作材料的影响,为方便施工,应与工程主体材料相互利用。
(4)地形和地质条件满足预制梁的生产要求并能尽量减少临时工程量。
1.2 预制梁场选址的影响因素
除了遵守上述几项原则之外,预制梁场选址根据项目的生产、进度、工期以及成本的不同要求,其位置选择有很大的区别。因此,在这里总结以下几个方面的因素影响[2]:
(1)场地因素,是否具有合适作业面积的场地。
(2)运输因素,对外交通和对内交通条件是否便利。
(3)费用因素,在保证预制梁的生产效率和质量的前提下,工程成本控制是施工单位考虑的主要目标。
综上所述,一般情况下预制梁场选址思路如图1所示。
2 三角模糊决策模型
目前模糊数学的相关方法在工程施工中已经广泛应用,不断参照具体适用工程,其研究已经取得巨大的成功[3]。我们可以利用多属性模糊决策理论对预制梁场场内布置方案进行评价,建立模糊多属性决策模型进行计算,并验证其结果是否与项目实际相符合。
2.1 建立评价指标体系
根据预制梁场布置的依据以及影响因素分析,设计方案评价体系见图2。
(1)生产安全性:指预制梁场的场内布置设计是否能够保证施工人员安全。
(2)基本生活条件:劳动者在整个工程顺利进行中属于不可缺少的部分。
(3)生产便利程度:根据预制梁生产工序的要求,安排合理的空间布局,在生产预制梁时各种资源的使用有比较好的流水作业线路,避免回流作业,增加成本。
(4)对外交通:若对外交通方便快捷,显然能够增加生产效率,有利于成本控制。
(5)内部交通:预制梁生产是一个连续的过程,各个相关功能区的运输需方便快捷,并且尽可能减少运输距离,提高工作效率,节约成本。
(6)梁体运输:在预制梁场设计布置时,必须将梁体运输的运输工具、道路情况充分考虑以满足生产施工需求。
(7)机械化程度:为了提高预制梁场的生产效率,预制梁场在设计的时候应该最大限度发挥机械设备的作用。
(8)土地利用率:预制梁场的布置应该因地制宜,力求以最小的布置用地达到最大的生产力度,满足项目工程的需要。
(9)梁台和模具利用率:通过比较精确的定量分析得到合理的生产设计,保证工程能够按时按质完成目标。
(10)租地与征地费用:通常是采用租赁的形式来获得场地使用权,要合理地进行租地与征地,在不影响工程进度的情况下,尽可能地节约成本。
(11)场地平整费用:不同的地段,因其地质情况不同可能平整地面的费用也不相同,因此,在合理满足工程需要的情况下,须尽量减少土地的平整费用。
(12)设备运行和劳动力成本:合理地对机械设备和人工劳动力需求进行分析,得到最适合的配比,达到比较好的成本控制目标。[4]

图2 评价指标体系示意图
2.2 构造模糊决策模型
模糊多属性决策模型相对于传统的经典多属性决策模型来说,多了一个模糊因子,使最后的决策更加合理。下面对该模型进行定义:令被评价的方案的集合为C={C1,C2,…,Cm},每一个方案都有一个自己的属性,故令属性集为D={D1,D2,…,Dn},与此同时,每一个属性的重要程度不一样,因此令其相对重要程度权重的集合为ω={ω1,ω2,…,ωn},但是,在实际的应用中,指标属性和其权重一般都是语言描述的,有的描述很准确,有的就比较模糊,例如:“不行”表示确定不好,“可能”则表示很模糊,因此,必须利用模糊子集或模糊数来度量这些指标属性和权重,将具有不确定性的属性指标、权值和语言描述等都定义成相应的模糊子集或模糊数。其模糊指标矩阵可以定义为R:
(1)
于是模糊决策矢量可表示为:
W=ω⊙R={w1,w2,…,wn}⊙

(2)

2.2.1 建立综合三角模糊数互判矩阵
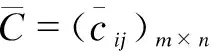

(3)

2.2.2 计算评价指标的三角模糊数权重
(4)
2.2.3 建立综合三角模糊数属性评价矩阵
一般情况下,我们将传统的评价语言转化为具体的数字来表示。但是,数字一旦定下就是一个固定不变的精确值了。然而,对于评价来说,过度的精确评价显然是不现实的,也不客观。因此,为了追求更高的准确性和客观事实性,本文利用三角模糊数来对语言变量进行描述。为了让计算更加简便,建立权重相同的三角模糊数等级,此处与语言描述相对应的三角模糊数等级见表1。

表1 语言描述和三角模糊数的转换关系表
每位专家根据三角评估指标,结合表1中的模糊语言变量数量,建立综合三角模糊数评估方案得分矩阵,然后通过综合模糊评估方法的叠加获得专家权重,综合三角模糊数评估方案得分矩阵如表2所示。
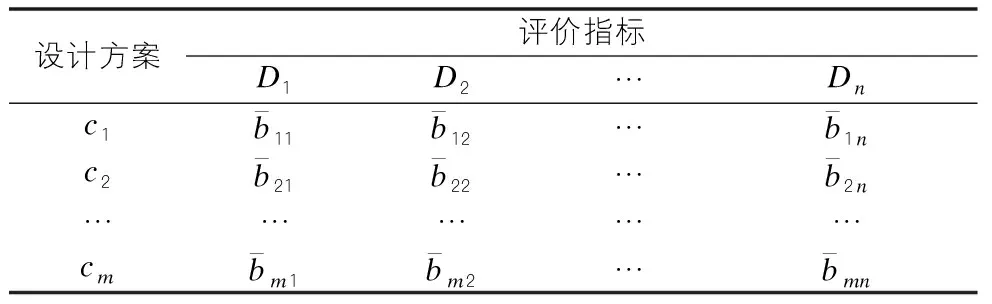
表2 综合三角模糊数评估方案得分矩阵表

2.2.4 计算三角模糊数总评结果

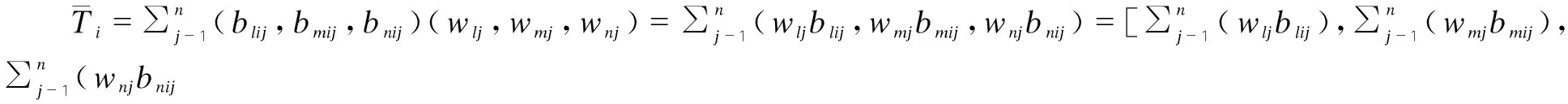
(5)
2.2.5 对被评价方案总评结果的三角模糊数进行排序决策

(6)

3 应用实例
广西某高速项目标段,沿线地质条件复杂,是该项目最为突出的一个特点。途经喀斯特岩溶地貌区,山岭重丘区,地面起伏大,山体陡峭、沟壑冲槽分布广泛。为了满足高等级公路所需的技术标准,克服各种不利地形,该高速公路主线的桥梁隧道总长超过70 km,桥隧比高达34.3%,这一比重仅次于河池至百色高速公路。
对常见的预制场以及广西某高速项目标段预制梁场的布置设计进行评价,分析得到三个预制梁场的布置方案中最符合工程实际需求的布置方案,并对其最后的结果评价,辅助决策者做出正确的选择。在评价之前,应该找到具有一定权威的专家组成专业评分小组:三位专家的评分结果组建三角模糊互补评价指标矩阵,另有五名专家建立属性评分矩阵。[5]方案分析如下:
3.1 建立综合三角模糊数互判断矩阵

3.2 计算评价指标三角模糊权重
根据公式(3)、(4),利用MATLAB编程进行数据计算,最终得到关于评价指标的三角模糊数权重值,见表5。
3.3 建立综合三角模糊属性评分矩阵
专家打分后,对评分结果进行汇总分析,假设每位专家都具有相同的权威性,方便计算,取等权重wr=1/3,计算结果如下页表6所示。

表6 综合三角模糊数评价矩阵表
3.4 计算三角模糊数总评分值
根据公式(5),对专家判断信息进行汇总分析得到评价对象的最终三角模糊总评分值如表7所示。

表7 三角模糊总评分表
3.5 计算评价对象的三角模糊数总分值的期望值排序
根据公式(6),计算评价对象的三角模糊数期望如表8所示。

表8 三角模糊总评分的期望值表
最后,决策者可以根据表8中的评价对象的总体评估水平的预期值和项目实际情况做出全面的决策。如果仅考虑本文所列指标,应选出具有最高预期值的方案,符合项目实际情况。
4 结语
本文在总结施工经验的基础上,系统分析了基于模糊数学理论的道路桥梁工程预制梁场的选址与设计。主要研究结果如下:
(1)对比分析了各类型预制梁场特点,总结预制梁场选址的原则与影响因素。
(2)分析预制梁场场内细观布置的影响因素,从工作环境、交通条件、资源利用、生产成本等四个方面建立预制梁场场内细观布置方案的评价指标体系,考虑细观布置方案属性指标的随机性与模糊性,运用三角模糊数方法,构建预制梁场场内细观布置方案优选模型。
(3)以广西某高速公路中第二标段项目为实例,利用上述模型进行预制梁场的宏观选址和细观场内布置方案优选,并与项目实际布置情况进行对比分析,验证了本文理论模型的可行性与合理性。
