稳态流下非饱和土地基承载力模型
2018-11-13陈茜程大伟
陈茜,程大伟
(1.陕西理工大学 土木工程与建筑学院,陕西 汉中723001; 2.长安大学 环境科学与工程学院;旱区地下水文与生态效应教育部重点实验室,西安 710064)
地基承载力问题是土力学的经典问题之一[1-3],可用极限平衡法和极限分析法进行分析。作为典型公式的普朗德尔无重介质地基极限承载力公式,在建立地基极限承载力和滑动面的基本物理概念和分析途径上具有重要作用。
岩土工程中所遇土体多为非饱和土,降雨或地下水位抬升往往引起土体内含水量和吸应力的变化[4-7],从而对非饱和土地基承载力产生影响。近年来,学者们通过试验研究和理论分析对非饱和土地基极限承载力开展了大量研究。张常光等[8-9]在对现有非饱和土抗剪强度进行拓展的基础上研究了基质吸力均匀分布和线性分布下地基极限承载力和地基临界荷载。李艳等[10]以三剪统一强度准则及非饱和土双应力状态变量抗剪强度公式为基础,推导了非饱和土条形地基太沙基极限承载力的计算公式。马少坤等[11]利用增量加载的有限元法,对比分析不同饱和度对刚性和柔性地基承载力的影响。孟长江等[12]以Fredlund和包承纲非饱和土强度公式为基础,分析了考虑常吸力条件下的非饱和土地基承载力。侯建军等[13]通过平板载荷试验和静力触探,分析浸水前后黄土地基承载力损失规律。已有研究往往忽视了非饱和土中吸应力剖面非线性特点对地基承载力的影响,或者缺少关于吸应力剖面非线性特点对地基极限承载力影响的机理分析。
笔者拟在对普朗德尔基本假定进行补充的基础上,推导稳态流下能够考虑吸应力剖面影响的地基极限承载力公式,分析不同地下水位埋深和比流量对地基极限承载力的影响。
1 基本假设与模型
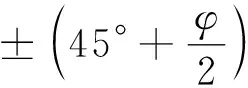

图1 无重介质滑动面Fig.1 Slip surface of weightlessness
文献[14]基于普朗德尔假定及普朗德尔所确定的滑动面形式,利用刚体平衡方法获得了与普朗德尔地基极限承载力相同的解答。具体做法是,将地基中滑动土体沿Ⅰ区和Ⅲ区中线切开,如图2所示,取土体OCEGO作为隔离体,利用静力平衡,即对极点A的合力矩为零进行求解。其中,OA边为待求极限承载力pu,AG边为侧荷载q,OC边为朗肯主动土压力pa,GE边为朗肯被动土压力pp,对于饱和土土压力沿深度方向均匀分布(图2中虚线所示),CE边为粘聚力c及正压力与摩擦力的合力为R。稳态流下非饱和土主动土压力分布具有明显的非线性分布特点[15],如图2中实线所示。
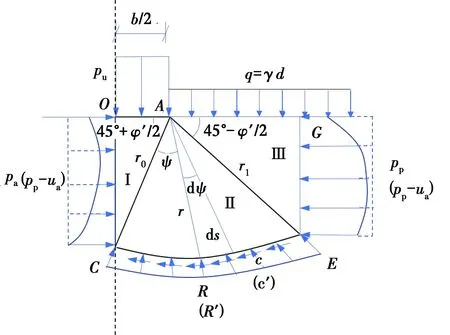
图2 力矩平衡法求极限承载力Fig.2 Balance force method for ultimate bearing capacity of soil
为了便于将普朗德尔地基极限承载力公式拓展到稳态流下非饱和土地基承载力计算情形,作如下补充假定和修正假定:
1)地基土滑动面符合普朗德尔所确定的滑动面形式,可用刚体平衡方法求解。
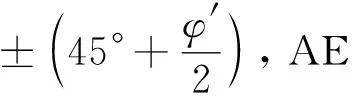
r=r0eψtan φ′
(1)
式中:r为对数螺旋线任意点到极点A的距离;r0为对数螺旋线初始半径;ψ为射线r与r0夹角;φ′为有效内摩擦角。
3)仅考虑竖向稳定渗流的影响,则OC边为朗肯主动土压力(pa-ua)、GE边为朗肯被动土压力(pp-ua)分别为[15]
χ(ua-uw)(1-Ka)
(2)
χ(ua-uw)(Kp-1)
(3)
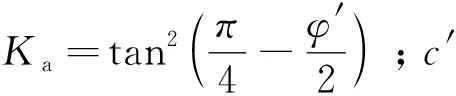
稳态渗流条件下吸应力χ(ua-uw)的解析分布函数[15]为
χ(ua-uw)=-
(4)
式中:α和n是Van Genuchten模型拟合参数;q为比流量即降雨量或蒸发率;ks为饱和渗透系数;γw为水的重度;z为到地下水位处的距离。
4)滑动面CE边为有效粘聚力c′及正压力与摩擦力的合力R′,R′指向A点。
由于隔离体处于静力平衡状态,各边界面上的作用力对极点A取矩,应满足
∑MA=0
(5)
其中,几何关系为
OA边长度
(6)
OC边长度
(7)
对数螺旋线初始半径
(8)
对数螺旋线终止半径
(9)
GE边长度
(10)
AG边长度
(11)
弧面CE边上有效黏聚力对极点A产生的力矩Mc′可由式(12)求得。
(12)

(13)
AG边上侧向荷载q对极点A产生的力矩Mq为
(14)
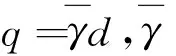
OA边上地基极限承载力pu对极点A产生的力矩Mpu为
(15)
OC边上朗肯主动土压力(pa-ua)对极点A产生的力矩Mpa为
(16)
式中:l为任意点处的力臂长度。为了便于求解稳态渗流条件下吸应力χ(ua-uw)的解析分布函数,将式(16)转化为对深度z积分,则有
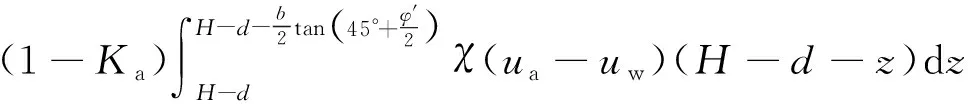
(17)
式中:d为基础埋深;H为地下水位埋深。
同理可得,GE边上朗肯被动土压力(pp-ua)对极点A产生的力矩Mpp为

(18)

将式(13)、(14)、(15)、(17)、(18)代入式(5)可得
Mpu+Mpa=Mq+Mpp+Mc′
(19)
整理并化简,则有

(20)
对比稳态渗流条件下非饱和土地基极限承载力式(20)与饱和土普朗德尔地基极限承载力公式可以发现,由于饱和土吸应力χ(ua-uw)为0,式(20)能退化到与饱和土普朗德尔地基极限承载力公式完全相同的形式,表明建议的稳态渗流条件下非饱和土地基极限承载力具有合理性。
2 计算与分析
稳态流下非饱和土的吸应力垂直分布规律主要受比流量q、地下水位埋深H、渗透系数ks、Van Genuchten模型拟合参数αv和n等因素控制。算例中取基础宽度b为2 m,基础埋深d为1.5 m,土的干重度γd为14.7 kN/m3,有效内摩擦角φ′为20°,有效黏聚力c′为10 kPa,残余含水量θr为0.03,饱和含水量θs为0.2,饱和渗透系数ks为5×10-8m/s,Van Genuchten模型拟合参数αv为0.04 kPa-1和n为3,用于计算分析不同比流量q和地下水位埋深H对地基极限承载力的影响。
首先计算分析不同地下水位埋深H对地基极限承载力的影响。取比流量q为-5×10-9m/s,负号表示入渗,地下水位埋深分别为3.6、4.6、5.6、7.6、8.6、9.6、10.0 m,则相应的地基极限承载力与地下水埋深关系如图3所示。

图3 地基极限承载力与地下水埋深关系Fig.3 Relationship between ultimate bearing capacity of soil foundation and groundwater
图3所示的地基极限承载力与地下水埋深关系表明,稳态流下非饱和土地基极限承载力随地下水位埋深的减小呈先递减再增大的变化趋势。这主要是因为,在比流量q相同的稳态流情况下,地下水位的变化实质上使得滑动土体处于不同的吸应力剖面区段,而稳态流下吸应力剖面具有明显的非线性特征。当地下水位埋深为10 m时,对于无粘性土、粉土以及粉质黏土,吸应力随深度增加呈现出先增大至某个峰值然后减小的特点[15],可依次分为吸应力增大区段、吸应力峰值附近区段和吸应力减小区段。算例中地下水位埋深为10 m时吸应力剖面如图4所示,图中10 m处为地表。地下水位埋深减小,会使得滑动土体依次处于吸应力增大区段、吸应力峰值附近区段和吸应力减小区段,从而导致地基极限承载力随地下水位埋深的减小呈先递减再增大的变化趋势。

图4 吸应力剖面
在计算分析不同比流量q对地基极限承载力的影响时,取地下水位埋深为5.6 m,比流量q分别为-5×10-12、-5×10-11、-5×10-10、-1×10-9、-5×10-9、-1×10-8、-2×10-8m/s,则相应的地基极限承载力与比流量关系如图5所示。
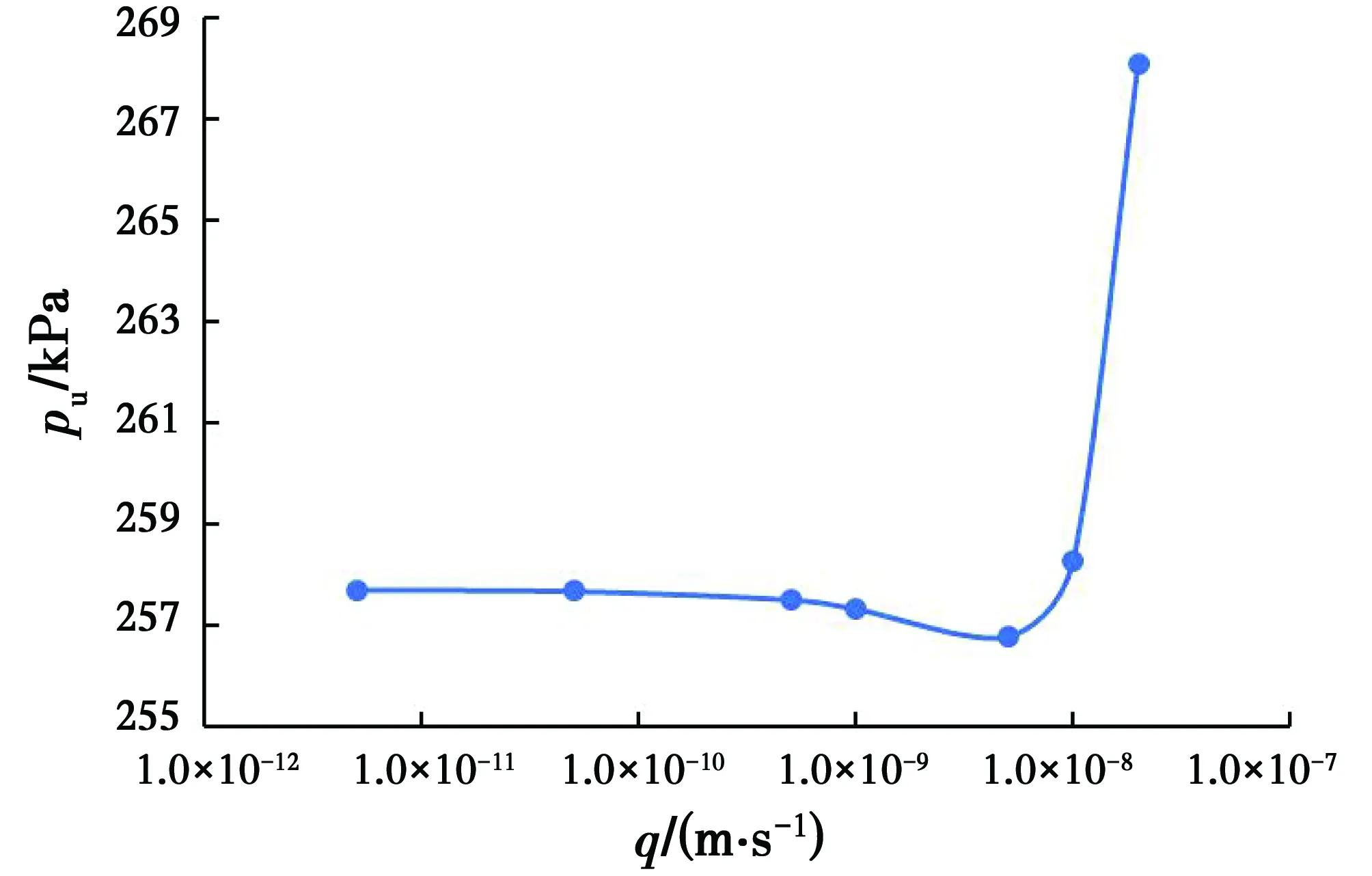
图5 地基极限承载力与比流量关系曲线Fig.5 Relationship between ultimate bearing capacity of soil foundation and specific
图5所示的地基极限承载力与比流量关系表明,稳态流下非饱和土地基极限承载力随比流量的增大呈先减小再增大的变化趋势。这主要是由于比流量增大引起滑动土体所在范围的吸应力呈现出非线性变化规律造成的。在算例中,不同比流量q条件下的吸应力剖面如图6所示,地表位于5.6 m处,滑动土体的Ⅰ区在2.7~4.1 m区间,Ⅲ区在2.3~4.1 m区间。由图6可见,在这两个区间内吸应力均随比流量的增大呈现出先增大后减小的趋势,从而导致地基极限承载力随比流量的增大呈先减小再增大的变化趋势。
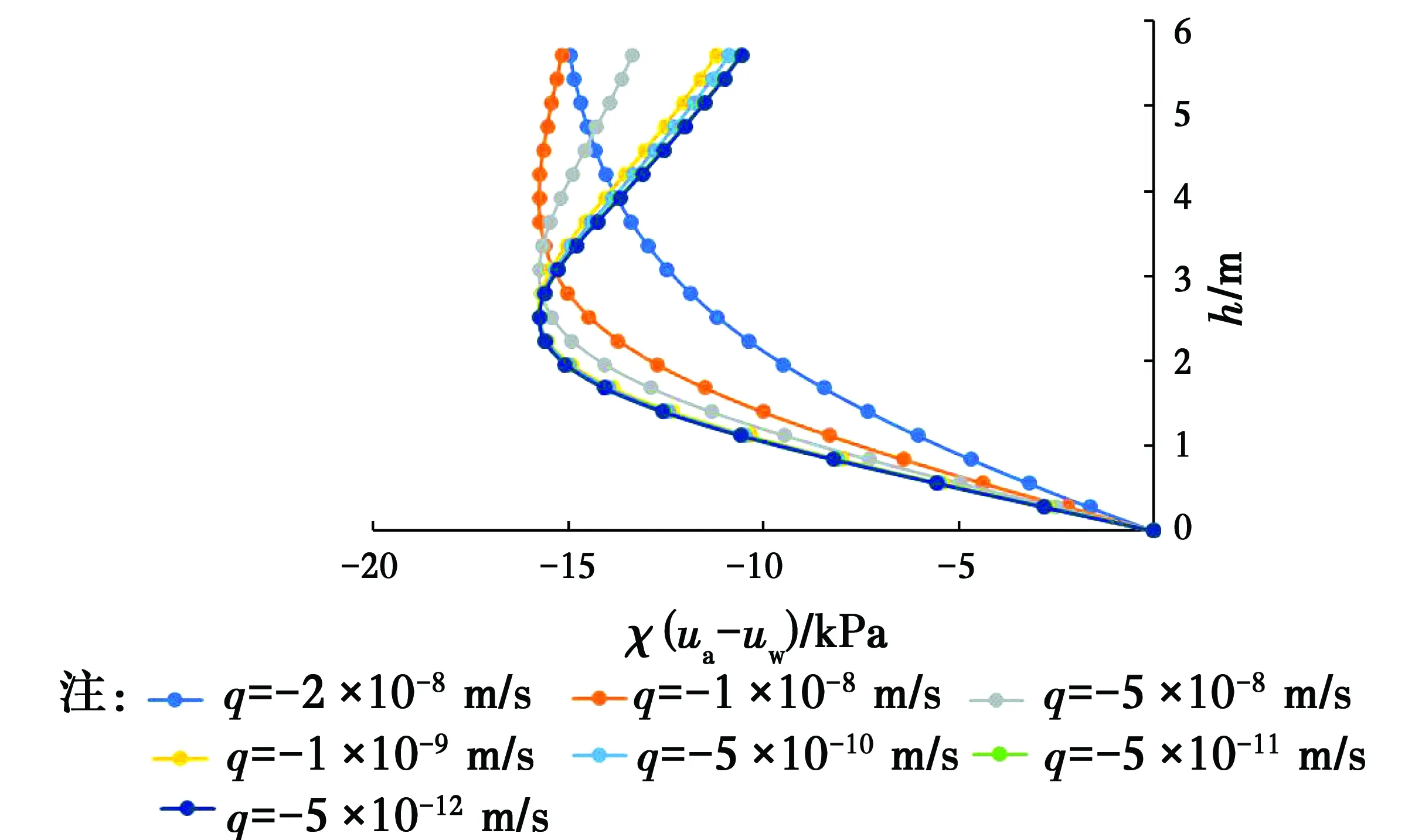
图6 不同比流量下吸应力剖面Fig.6 Suction stress profile under different specific
3 结论
基于普朗德尔确定的滑动面形式,通过对普朗德尔假定进行补充,利用刚体平衡方法推导了稳态流下非饱和土地基的极限承载力,并讨论了地下水埋深和比流量变化对地基极限承载力的影响。
1)在仅考虑竖向稳定渗流条件下,引入非饱和土朗肯土压力公式,利用静力平衡条件,推导非饱和土地基的极限承载力公式;与普朗德尔公式相比,该公式考虑了滑动土体内吸应力对地基极限承载力的影响。
2)稳态流下吸应力剖面的非线性特征是导致非饱和土地基极限承载力随地下水位埋深表现出非线性变化规律的重要因素;当土吸应力随深度增加呈现出先增大后减小的特点时,相应的地基极限承载力表现出随地下水位埋深的减小呈先递减再增大的变化趋势。
3)比流量增大引起滑动土体所在范围的吸应力非线性变化的特点导致非饱和土地基极限承载力随比流量变化亦表现出非线性变化趋势;当滑动土体内吸应力随比流量的增大呈现出先增大后减小的趋势时,地基极限承载力随比流量的增大呈先减小再增大的变化趋势。
