平行节理相互作用对节理岩体的力学行为影响

王飞，曹平，曹日红，高青鹏，熊心广，王柱



平行节理相互作用对节理岩体的力学行为影响

王飞，曹平，曹日红，高青鹏，熊心广，王柱

(中南大学 资源与安全工程学院，湖南 长沙，410083)

以类岩材料制作平行节理试样并开展压剪实验，采用声发射系统监测试样加载过程，研究节理相互作用对岩体力学行为的影响。研究结果表明：1) 节理试样在压剪加载下可分4种破坏模式：共面剪切破坏；沿节理面剪切破坏；沿剪切应力面剪切破坏；类完整型剪切破坏。倾角对试样破坏模式起决定性作用，重叠度影响试样裂隙的发育。2) 试样峰值剪切强度随倾角增加先增大后减小并在45°取得最大值；随着节理重叠度的增大，峰值剪切强度逐渐减小；剪切峰值强度对倾角因素更敏感。3) 不同倾角试样的剪切应力−位移曲线差异主要体现在破裂后阶段，试样的声发射计数变化规律与破坏模式相对应；不同重叠度试样应力−位移曲线形态相似，试样的声发射计数变化规律相似，但计数峰值随重叠度的增大逐渐减小。

节理相互作用；节理重叠度；压剪试验；力学行为；声发射

天然岩体内部发育的原生节理、裂隙、断层等不连续面会极大的削弱岩体的稳定性，进而使岩体力学性质的稳定性评估成为岩土工程中的一个普遍问 题[1−2]。不连续面对岩体力学性质的影响不仅在于其与岩石的相互作用，还在于不连续面之间的相互作 用[3−4]。岩体内部的原生节理间会产生相互影响，且在荷载下会形成相互贯通造成岩体的进一步破坏，并进一步弱化岩体的强度，最终影响岩体工程的整体稳定性。节理之间相互作用对岩体破坏的影响规律将对实际工程有重要的指导意义。国内外学者通过试验及数值模拟等方法对断续节理岩体的力学行为进行了广泛研究。PRUDENCIO等[5]对具有非连续节理的岩石进行了双轴压缩试验，研究结果表明非连续节理的几何形状、主应力的方向对岩石的破坏模式有重要影响。CAO等[6]通过遍布非连续节理类岩石试样进行单轴压缩试验，提出了4种破坏模式。CORDING等[7]发现了与节理组几何形态和围压有关的4种破坏模式：沿单一面滑移、台阶式破坏、多平面台阶式破坏和贯穿完整岩块的剪切破坏。杨圣奇等[8−10]采用断续节理大理岩试件研究了裂隙参数几何分布对其变形及破坏的影响，结果表明变形呈现出局部化渐进破坏特征，峰值强度、弹性模量等均有明显降低。陈新等[11−12]研究了单轴压缩下预制张开非连续裂隙节理组的产状和连通率对压缩强度、弹性模量及应力−应变曲线的影响。蒲成志等[13]对预制非连续多裂隙试件进行单轴压缩试验，并运用FLAC3D建立应变软化模型进行数值模拟，探索裂隙角度和分布密度对试件断裂破坏强度的影响规律。FAN等[14]采用PFC3D数值模拟软件研究非连续节理倾角、节理连通率对岩石力学行为的影响，结果表明节理倾角、连通率对岩石的强度、变形模量有重要影响。上述学者的试验和数值模拟研究揭示了节理对岩体的重要影响。在预置断续裂隙试件的研究中，绝大多数采用不同的几何分布裂隙进行单轴、双轴压缩以研究裂隙扩展、汇合贯通和岩体破坏模式，但剪切试验条件下的研究相对较少，尤其是针对压剪应力同时作用下的岩体破坏行为；大多数是对节理与岩桥之间的关系进行研究[15−16]，但节理之间的相互作用研究的相对较少，缺乏关于裂隙组合下与岩体力学行为定量关系的试验研究。然而，在现实岩体工程开挖中，节理岩体往往处于压剪综合应力环境且节理之间经常相互作用，如高陡岩质边坡等。因而，本文作者针对压剪应力下的节理相互作用对岩体力学行为的影响尚缺乏可靠的理论、试验研究，通过预制平行节理类岩试样进行压剪试验，系统研究节理倾角、重叠度相互作用下的岩体力学性质。

1 试验

1.1 试件制备

试验中的遍布节理闭合试样由水泥砂浆材料浇筑而成。白水泥、细砂、水按体积比2:1:1配置试验用水泥砂浆，在室温下浇筑到磨具中成型。试样高×宽×厚为100 mm×100 mm×30 mm，其中预制节理采用内插云母片制成，云母片厚度为0.6 mm。试件几何参数及节理分布如图1所示。其中：0为节理重叠长度，mm；r为节理间岩桥长，固定取20 mm；j为节理长度，固定取15 mm；为节理间距，固定取15 mm；为节理倾角，(°)。试样中设置4种不同节理重叠长度(0为15，10，5和0 mm 4种)，每种重叠长度节理设置6种不同倾角(倾角为0°，30°，45°，60°，75°和90°)，试样节理倾角变化遵循平行转动的规律。

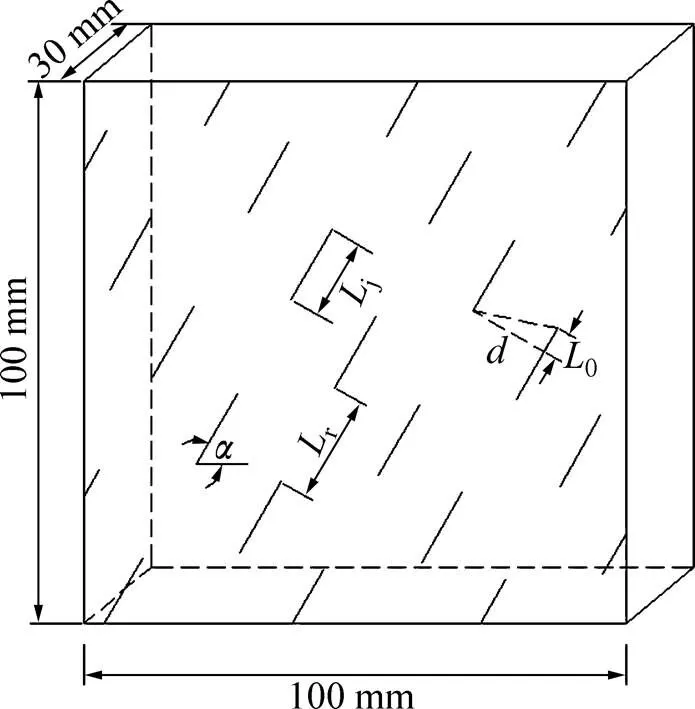
图1 试件几何参数及节理分布

水泥砂浆浇筑后在室温下养护24 h后拆模，再在养护箱中养护28 d后进行试验。对于相同节理布置的试件，进行完全相同的3次重复试验。在同一类型试件试验中，剔除试验强度离散性较大的试件，选取平均值作为该类型试件的代表性试验结果。本次试验中每个试样被分配1个ID号如S-a-b(S代表试样，‘a’代表试样节理重叠长度0，‘b’代表节理倾斜的角度)。完整类岩材料力学参数如表1所示。

1.2 试验方法

试验研究采用倾斜压模剪切法，固定压剪角为45°。试验加载仪器采用高精度微机控制电液伺服试验机，采用位移控加载方式，速度为0.1 mm/min。在试验过程中，采用高清数码相机记录试件表面破坏过程，采用声发射监测试样的内部破坏过程，以便于后期对试件破坏进行分析，试验装置示意图如图2所示。

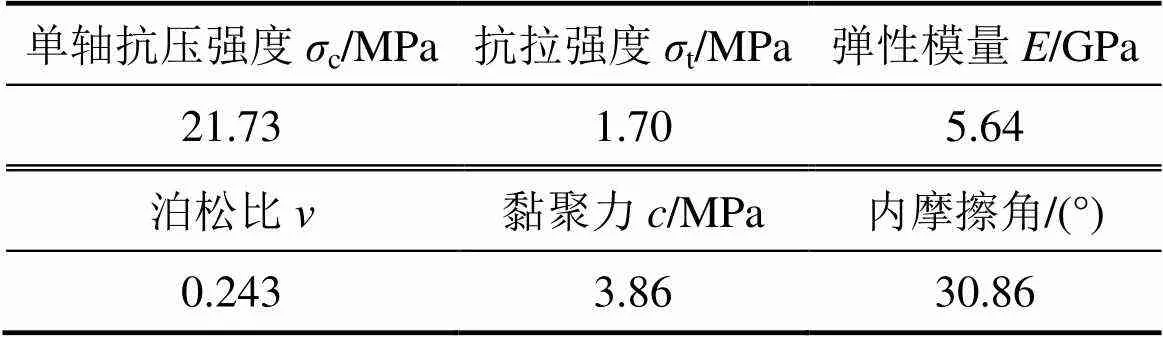
表1 岩石材料的力学参数

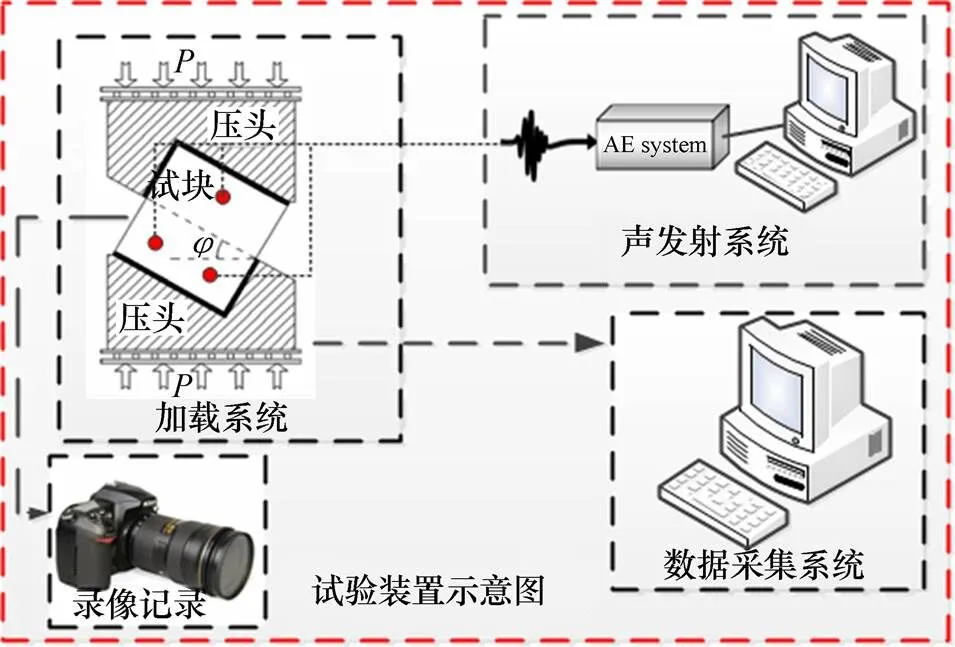
图2 现场试验装置示意图

2 节理相互作用对试样破坏模式的影响

预制节理对试样破坏行为具有重要作用，当荷载作用在单裂隙类岩石材料上时沿着原有裂隙会发育2种类型的裂隙(见图3)：拉伸裂纹和次生裂纹，次生裂纹根据沿节理面不同方向发育分为类平面次生裂纹和斜次生裂纹[6]。本文研究的压剪荷载可分解为沿试样中部平面的剪切荷载和沿上部加载的单轴压缩荷载(见图4)，且在45°压剪角下剪切荷载与轴向压缩荷载相等。

对于遍布节理试样，其力学破坏行为将更加复杂。对节理试样加载，节理周边将发育拉伸或次生裂纹，加载继续，裂纹之间会相互搭接形成多种破坏模式。根据压剪作用下破坏面与剪切应力作用面、节理面之间的关系，可将试样破坏划分为4种模式：共面剪切破坏(Ⅰ破坏模式)；沿节理面的剪切破坏(Ⅱ破坏模式)；沿着剪切应力作用面的剪切破坏(Ⅲ破坏模式)；类完整型剪切破坏(Ⅳ破坏模式)。

2.1 节理倾角对试样破坏模式影响

当平行节理倾角=0°时，图5(a)所示随着试样加载，在轴向压应力作用下试样左上部节理尖端先产生拉伸翼裂纹，随着荷载增强翼裂纹以断裂角70.5°向轴压荷载方向扩展，这符合经典断裂力学中有关翼形裂纹扩展的解析结果[17]。但随着荷载不断增大，剪切应力主导试样破坏，翼裂纹扩展没有得到延续且呈现出缓慢闭合的趋势，而试样中部剪切应力面与节理面共面两端节理先产生裂隙、进而克服两端岩桥使裂隙扩展，最终试样沿着共面完全贯通导致试件整体破坏。这种沿着节理面、剪切应力作用面进行裂隙扩展、贯通的平面剪切破坏的模式为共面剪切破坏模式(Ⅰ破坏模式)。这种模式由于剪切应力面与节理面共面以及剪切荷载与轴压荷载相等情况下先剪切破坏，因而这类试样的破坏路径是可以预判的，沿该共面贯通剪切破坏。

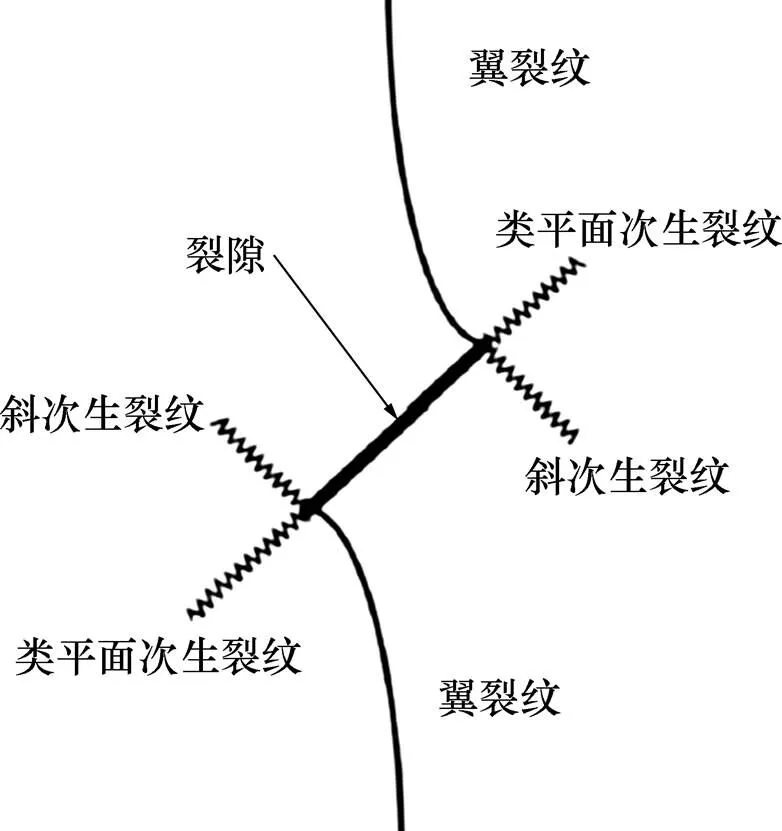
图3 原有裂隙在荷载作用下发育裂隙类型

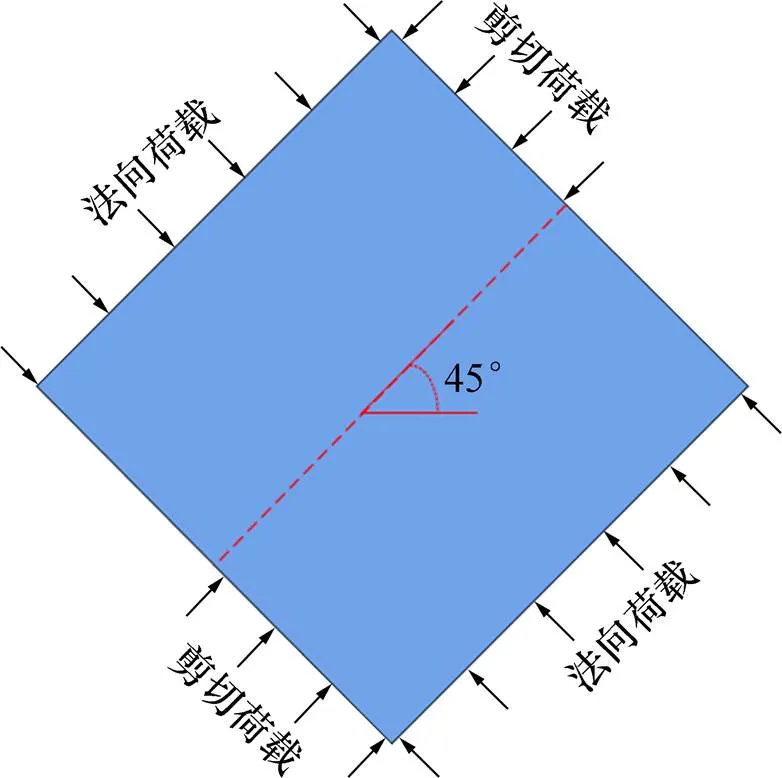
图4 剪切破坏模型

当平行节理倾角=30°时，剪切应力面与节理面相交，试样的破坏模式将复杂化。图5(b)所示在压剪应力作用下，试样产生了大量类平面次生裂纹(图3)。类平面次生裂纹先从试样剪切应力面两端附近节理尖端起裂，并沿节理面扩展、突破岩桥、贯通形成一个破坏面，这种破坏现象定义为沿节理面剪切破坏(Ⅱ破坏模式)。与30°类似，节理倾角60°时也为Ⅱ破坏模式。

(a) α=0°，Ⅰ破坏模式；(b) α=30°，Ⅱ破坏模式；(c) α=45°，Ⅳ破坏模式；(d) α=60°，Ⅱ破坏模式；(e) α=75°，Ⅲ破坏模式；(f) α=90°，Ⅲ破坏模式

当平行节理倾角=45°时，图5(c)所示试样节理尖端产生斜次生裂纹、类平面次生裂纹、翼裂纹且裂隙之间相互搭接，在试样中部附近形成不规则的剪切面，该试样的破坏形式类似完整试样的破坏，平行节理对试样弱化影响较小。这种破坏现象定义为类完整型剪切破坏(Ⅳ破坏模式)。

当平行节理倾角为75°和90°时，图5(e)和5(f)所示剪切应力面与节理面近似垂直，荷载作用下试样中部节理先产生翼裂纹且不断发育。随着载荷增大，剪切力逐渐增强且占主导地位，剪切面附近节理尖端发育斜次生裂纹并沿着剪切面的方向扩展，其与相邻节理翼裂纹之间不断搭接，最终试样在荷载的作用下形成沿与剪切面类似平行的贯通裂纹面，这种破坏模式定义为沿剪切应力面的剪切破坏(Ⅲ破坏模式)。

2.2 重叠度对平行节理试样破坏模式影响

节理倾角=0°，不同节理重叠度的试样破坏模式均为Ⅰ破坏模式。随着节理重叠度的减小，在轴压作用下试样上发育更多的翼裂纹，但随着荷载增强，沿剪切面的剪切应力主导试样的破坏且促进翼裂纹的闭合，剪应力突破中部剪切面上岩桥的阻挡贯通破坏试样。整体上，重叠度只影响在破坏试样上翼裂纹的数量及分布形态，不改变试样破坏模式。

节理倾角=30°，不同节理重叠度的试样破坏模式均为Ⅱ破坏模式。其破坏虽都为沿着节理面剪切破坏，但不同重叠度其沿着的节理面不同。重叠度越小，试样破坏所沿节理面越大、克服的岩桥越长，难度越大，其峰值剪切强度也会越大。节理倾角60°与30°的不同重叠度裂纹发育规律类似。

节理倾角=45°，不同节理重叠度的试样破坏模式均为Ⅳ破坏模式。不同重叠度试样均为从中部两端开始的圆弧式贯通破坏其与完整试样类似。不同重叠度破坏面有一定的差异，重叠长度为0 mm和15 mm的试样破坏从试样下部圆弧式贯通，而重叠长度为5 mm和10 mm的试样破坏面从试样上部圆弧式贯通。试样随着节理重叠度的增大，其破坏表面的次生裂纹不断增多，导致试样峰值剪切强度不断减小。

节理倾角=75°，不同节理重叠度的试样破坏模式为Ⅲ破坏模式。不同节理重叠度的试样表面裂纹的发育程度、分布有明显差异。重叠长度为0 mm和5 mm的试样由于试样中部节理交错分布、集中度不高，试样中部斜次生裂纹发育不充分、且左上部形成局部破坏；重叠长度为10 mm和15 mm的试样在剪切应力面上节理分布均匀且较密，裂隙集中在试样中部节理附近、扩展充分，且在右下部形成局部破坏。节理倾角90°与75°的不同重叠度裂纹发育规律类似。

3 节理相互作用对岩体强度的影响

节理试样进行压剪试验，节理试样的峰值剪切强度及其对应位移如表2所示。

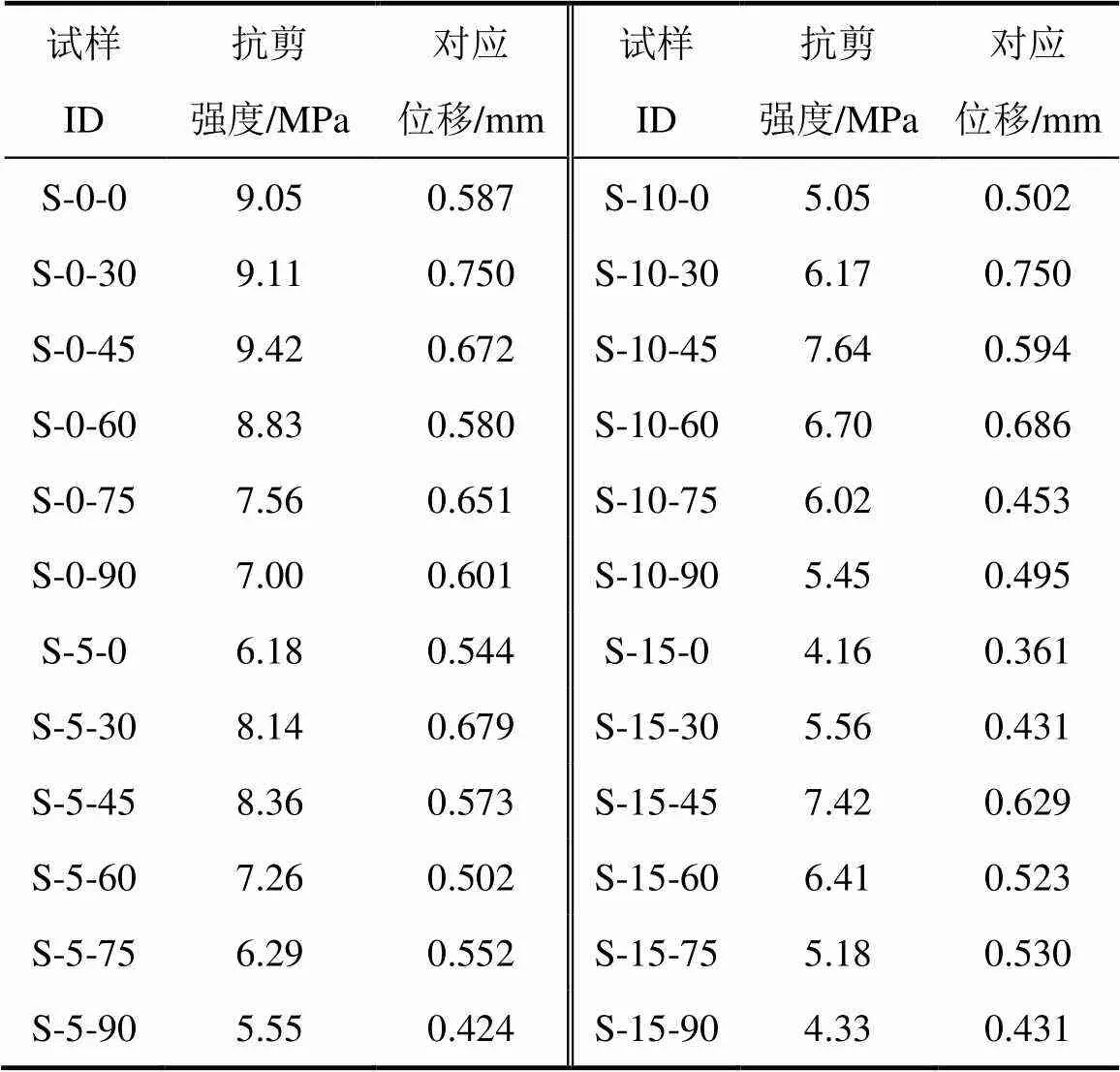
表2 节理试样的峰值剪切强度及对应位移

3.1 节理倾角、重叠度对试样抗剪强度的影响

节理倾角对峰值剪切强度有很大的影响且呈现一定的规律(图6)：当节理倾角从0°增加至45°时，试样的峰值剪切强度呈现出增长趋势；从45°增至90°时，随着角度增加峰值剪切强度开始不断减小；不同节理重叠度都在45°时达到峰值剪切强度最大值。当节理倾角=0°时，节理试样破坏模式为Ⅰ破坏模式，破坏面上节理裂隙最长、相对岩桥较短，且剪切应力沿该面集中施加荷载，因而易发生类平面剪切裂纹而导致最终破坏，其剪切强度相对较小。当节理倾角=30°时，节理试样破坏模式为Ⅱ破坏模式，裂纹以类平面次生裂纹为主，但其扩展方向受到节理倾角改变影响导致剪切应力无法集中作用到破坏面，其剪切强度增强。当节理倾角=45°时，节理试样破坏模式为Ⅳ破坏模式，节理弱化作用最小，峰值剪切强度最大。节理倾角=60°与30°类似，平行节理试样破坏模式为Ⅱ破坏模式，其峰值剪切强度较45°下降。当节理倾角为75°和90°时，节理试样破坏模式以Ⅲ破坏模式为主，节理方向与剪切应力面不断趋向垂直，节理在试样中部集中，裂纹发育以斜次生裂纹为主，剪切应力主导斜次生裂纹不断发育、扩展、贯通试样破坏，其峰值剪切强度较60°减小，90°相较75°更易破坏。

相同节理倾角下不同节理重叠度试件的峰值剪切应力，试样随着节理重叠度的增加其峰值剪切强度不断下降。不同节理重叠度的试样其节理密度是大致相等的，但改变了节理分布的均匀性。节理重叠度越小，节理在试样上的分布越均匀。在压剪应力作用下试样节理越集中其裂隙发育、扩展越容易，因而随着重叠度的增加试样的峰值剪切强度而减小。

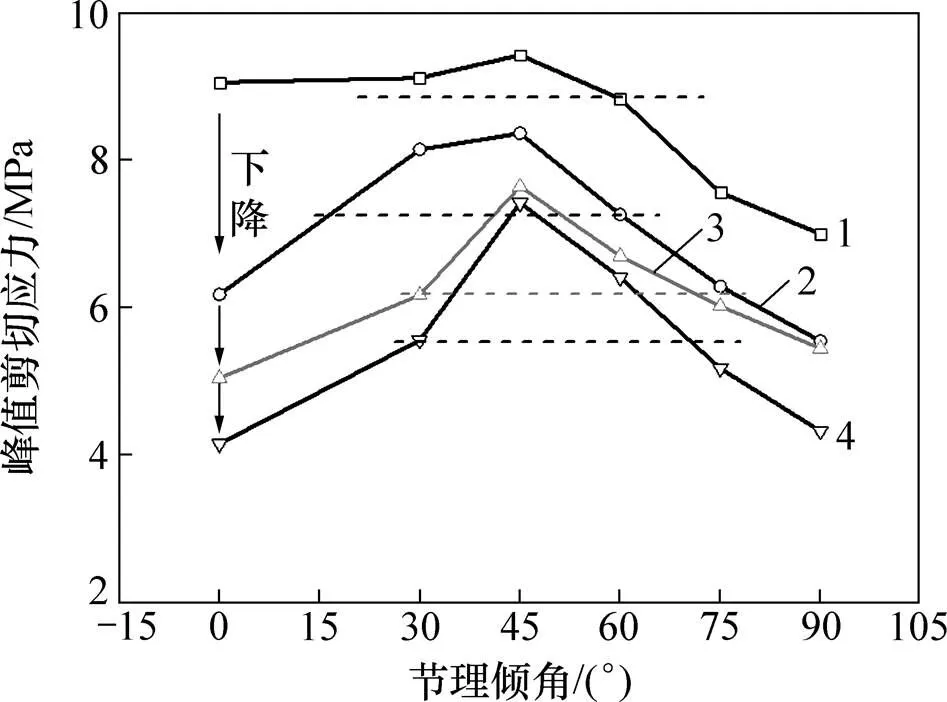
重叠度/mm：1—0；2—5；3—10；4—15。

3.2 试件峰值剪切强度的敏感性分析

采用敏感性分析旨在研究倾角、重叠度对峰值剪切强度的影响程度。由于倾角及重叠度的单位不一致，现将影响因素做常量处理。节理倾角范围为0~90°；节理重叠长度范围为0~15 mm。如倾角改变30°，做常量处理为1/3；改变节理重叠长度5 mm，做常量处理为1/3。

随着影响因素改变，峰值剪切强度呈非线性的变化，因而只能从影响因素引起目标值改变的斜率范围整体上体现目标值对因素的敏感性。倾角引起峰值剪切强度改变的斜率公式为

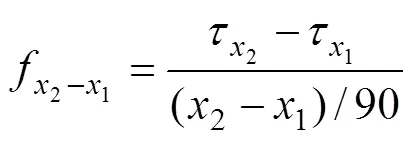
试验数据按照式(1)处理，得到倾角变化引起峰值剪切强度的改变斜率见表3。对表3数据进行绝对值处理可以得到：倾角对峰值剪切强度的影响斜率范围为0.18~11.16，其斜率所有数据绝对值后均值为4.992；倾角斜率的绝对值求和数值随重叠度的增加而增大，其表明节理重叠度越大(峰值剪切强度越小)，峰值剪切强度随倾角变化幅度越大。

表3 峰值剪切强度对节理倾角因素的敏感性

节理重叠长度引起峰值剪切强度改变的斜率公式为

试验数据按照式(2)处理，得到节理重叠度变化引起峰值剪切强度的改变斜率见表4。对表4数据进行绝对值处理可以得到：节理重叠长度因素对峰值剪切强度的影响斜率范围为0.30~8.61，其斜率所有数据绝对值后均值为2.985；随重叠度减小其对峰值剪切强度的斜率绝对值不断增大，因而随节理重叠度减小其对峰值剪切强度的影响不断增强；重叠度变化斜率绝对值求和数值随倾角呈现出先减小后增大的规律，这种变化规律与峰值剪切强度随倾角变化规律相反，其体现节理倾角在峰值剪切强度越大时其随节理重叠度变化斜率越小。

将表3和表4进行对比分析，倾角变化引起的均值斜率(4.992)大于重叠度变化引起的均值斜率(2.985)，其整体上表明剪切峰值强度对倾角因素更敏感，但随着节理重叠度的不断减小其对峰值剪切强度的影响不断增强。

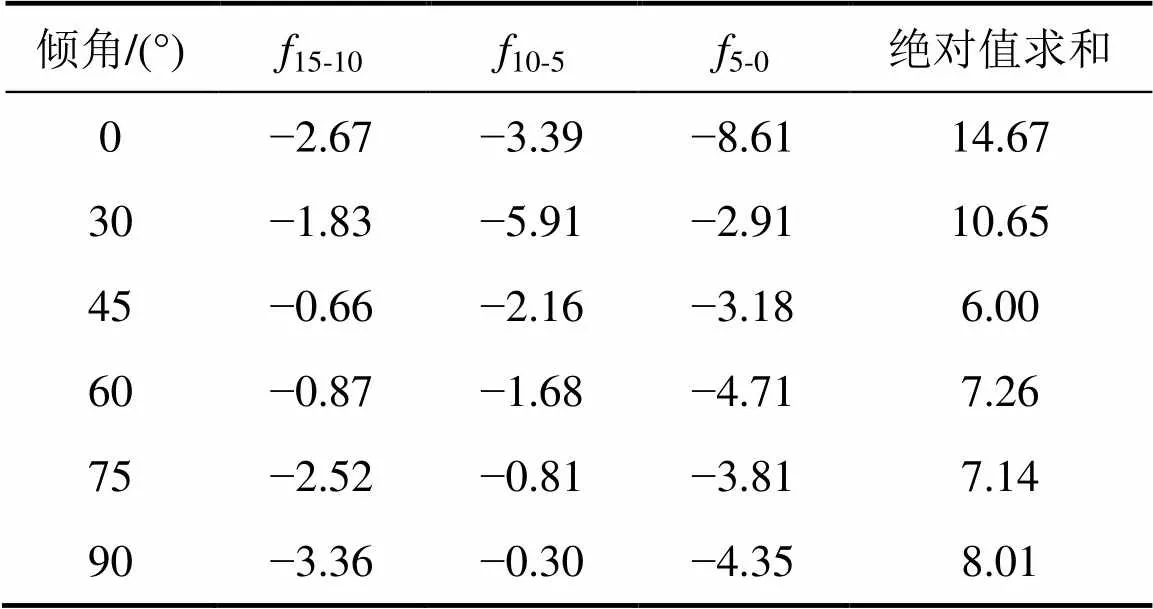
表4 峰值剪切强度对节理重叠度因素的敏感性

4 试样剪切应力−位移曲线及声发射分析

在节理试样破坏模式及强度研究的基础上，试样剪切应力−位移曲线结合声发射定量、全面、微观地反映试样裂隙开裂、扩展、贯通的过程[18]，加深对裂隙发育规律的研究有助于发现节理倾角、重叠度对曲线的影响以及剪切应力−位移曲线与破坏模式、强度的相关性，从而加深理解在压剪应力下节理试样的力学特性及破坏行为。

4.1 倾角对剪切应力−位移曲线的影响

结合试样受载直到破坏的声发射计数变化特征(图7)可将剪切应力−位移全过程曲线划分为4个典型的阶段：微裂隙闭合阶段()、弹性阶段()、裂隙扩展直到破裂阶段()和破裂后阶段()。微裂隙闭合阶段(Ⅰ)在岩石试样受载初期，由于内置节理裂隙及空隙受荷载闭合，类岩石被逐渐压密，形成早期的非线性曲线，声发射活动活跃、计数数值较大、变化幅度较大。弹性变形阶段(Ⅱ)岩桥所受的剪切应力与位移呈现线性关系，荷载作用下岩桥内部集聚大量弹性能，此阶段斜率明显高于微裂隙闭合阶段，裂隙发育较少，因而声发射计数降低且较为平稳。裂隙扩展直到破裂阶段(Ⅲ)曲线斜率逐渐减小且曲线在此阶段达到峰值剪切强度，试样节理开裂、扩展，应力不断克服岩桥抵抗导致裂隙逐步贯通，声发射活动从点开始计数增加，活跃程度逐渐增强，进而计数呈现几何式增长，最大值出现在此阶段。破裂后阶段(Ⅳ)随着位移增加剪切应力不断减小，岩桥被突破形成破坏面导致沿着裂隙产生局部摩擦滑动而出现应力突降，直到再次遇到抵抗产生残余强度，声发射计数相对峰值开始不断减小。

相同节理重叠度、不同节理倾角的剪切应力−位移曲线(图8)可以发现：试样随倾角变化其曲线会呈现出一定的差异性，除微裂隙闭合阶段曲线有一定的重合性其他各个阶段体现了明显的差异，破坏后阶段试样的差异性尤其明显。以重叠长度15 mm为例(见图8(a))，在破坏后阶段，45°试样产生应力突降，其他倾角应力缓慢下降，不同试样下降速率各不相同。应力下降速率与试样的破坏模式相关：45°试样破坏模式为类完整型剪切破坏，试样内部能够集聚大量能量突然释放导致试样破坏，其曲线产生应力突降现象；60°和30°试样破坏模式为沿节理面剪切破坏，破坏前能量集聚较多导致破坏后阶段曲线下降速率相对较快，仅次于45°时；75°和90°节理试样破坏模式为沿剪切应力面的剪切破坏，此倾角下峰值剪切强度较小，在加载过程中裂纹发育均匀，能量集聚量较少，其破坏后阶段应力下降速率较小；0°试样破坏模式为共面剪切破坏，峰后曲线相对平缓，其峰后曲线下降速率较小。

重叠长度为0 mm的试样(见图8(b))其破坏后曲线出现应力突降或多级应力突降现象，倾角为45°，30°，60°和0°的试样出现单级应力突降，倾角为75°和90°的试样出现多级应力突降；其曲线的下降速率与倾角的关系与重叠长度15 mm试样相同。对比2种重叠度试样，重叠长度为0 mm的试样破坏后曲线易产生应力突降，其下降速率较大。整体上，峰后曲线下降速率与试样峰值强度正相关。

根据重叠长度为0 mm的不同倾角试样声发射计数随剪切应力−位移曲线变化图(图7)可将声发射活动分为活跃期、平静期、激发期，不同倾角声发射活动情况各有差异。倾角为0°时，声发射计数在裂隙压密阶段相对活跃，弹性阶段进入平静期，裂隙扩展直到破坏阶段、破坏后阶段进入激发期且计数几何式增长。倾角30°的试样与倾角0°的试样声发射计数区别在活跃期计数变化幅度较大，在激发期峰值计数后下降速率快，这与该曲线应力突降相对应。倾角45°试样平静期相对较短，在激发期计数峰值前呈渐进增加其与试样破坏前的裂纹较多发育有关。倾角75°试样在裂隙扩展直到破坏阶段由于应力−位移曲线产生多级应力突降，因而声发射计数也呈现多次峰值。整体上，试样声发射计数变化规律与倾角相适应，试样的节理倾角对其破坏模式起到关键性作用，因而破坏模式与声发射计数的变化规律具有对应性。

4.2 重叠度对剪切应力−位移曲线的影响

不同重叠度试样的剪切应力−位移曲线(图8)可以发现：重叠度越小的试样其峰值剪切强度越大，峰值剪切位移也越大；不同重叠度试样曲线变化形态相似，但曲线斜率随重叠度变化而变化(尤其破坏后阶段)。节理倾角为0°的试样(见图8(c))，不同重叠度试样其曲线变化平缓，破坏后曲线渐进式下降，重叠度越小其下降速率越快。节理倾角为45°的试样(见图8(d))，破裂后阶段具有明显的应力突降，重叠度越小应力突降值相对越大。

从倾角为0°的不同重叠度试样声发射计数随剪切应力−位移曲线变化图(图7和图9)可以看出：不同重叠度声发射计数随应力−位移曲线变化形态相似；声发射计数峰值随重叠度的增大逐渐减小。声发射计数随应力−位移曲线变化形态相似在于试样破坏模式相同。试样的声发射峰值计数与其剪切强度正相关，由于剪切强度随重叠度增大而逐渐减小，因而试样的声发射峰值计数随重叠度增大也不断减小。试样峰值剪切强度越大其破坏释放能量越大、声发射峰值计数 越大。

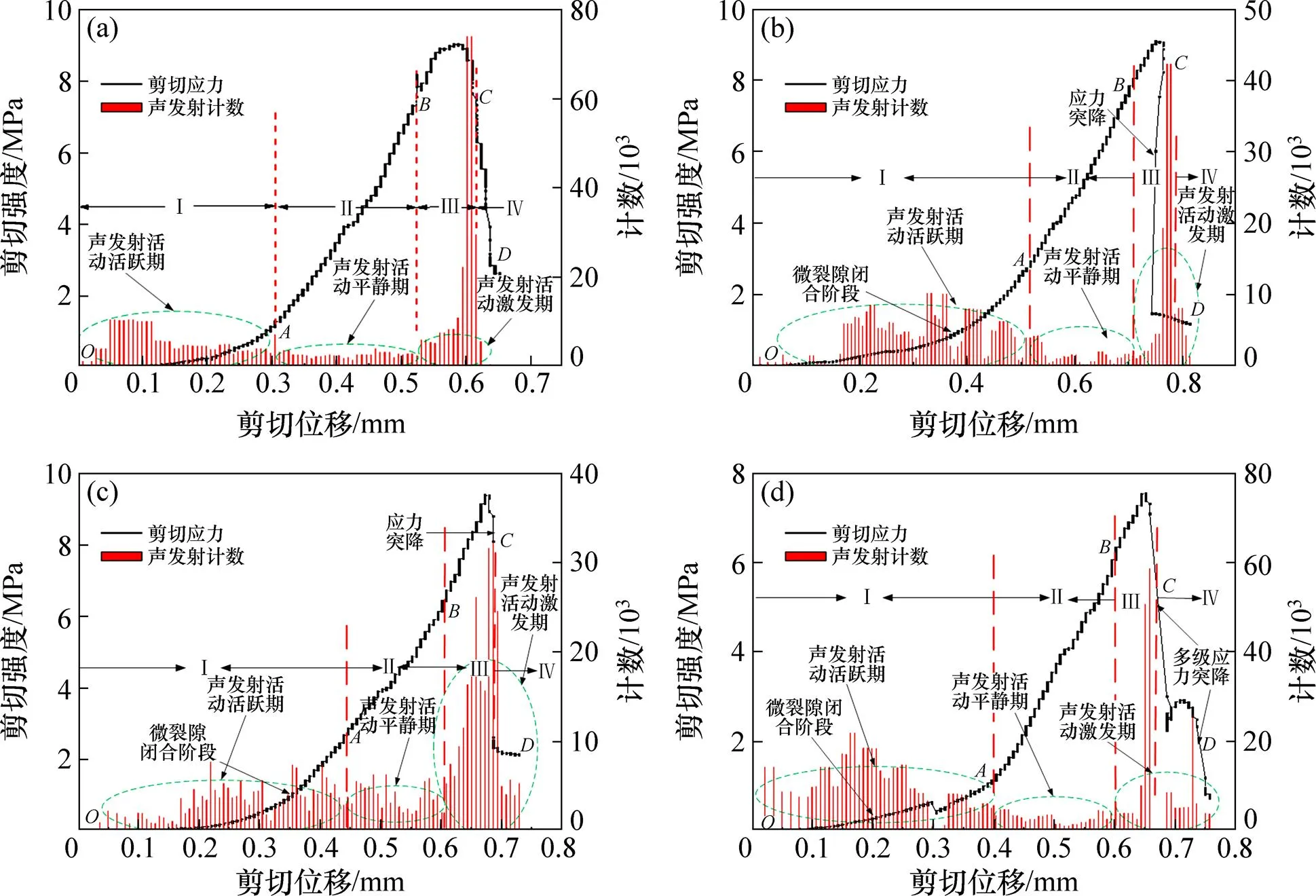
(a) S-0-0；(b) S-0-30；(c) S-0-45；(d) S-0-75

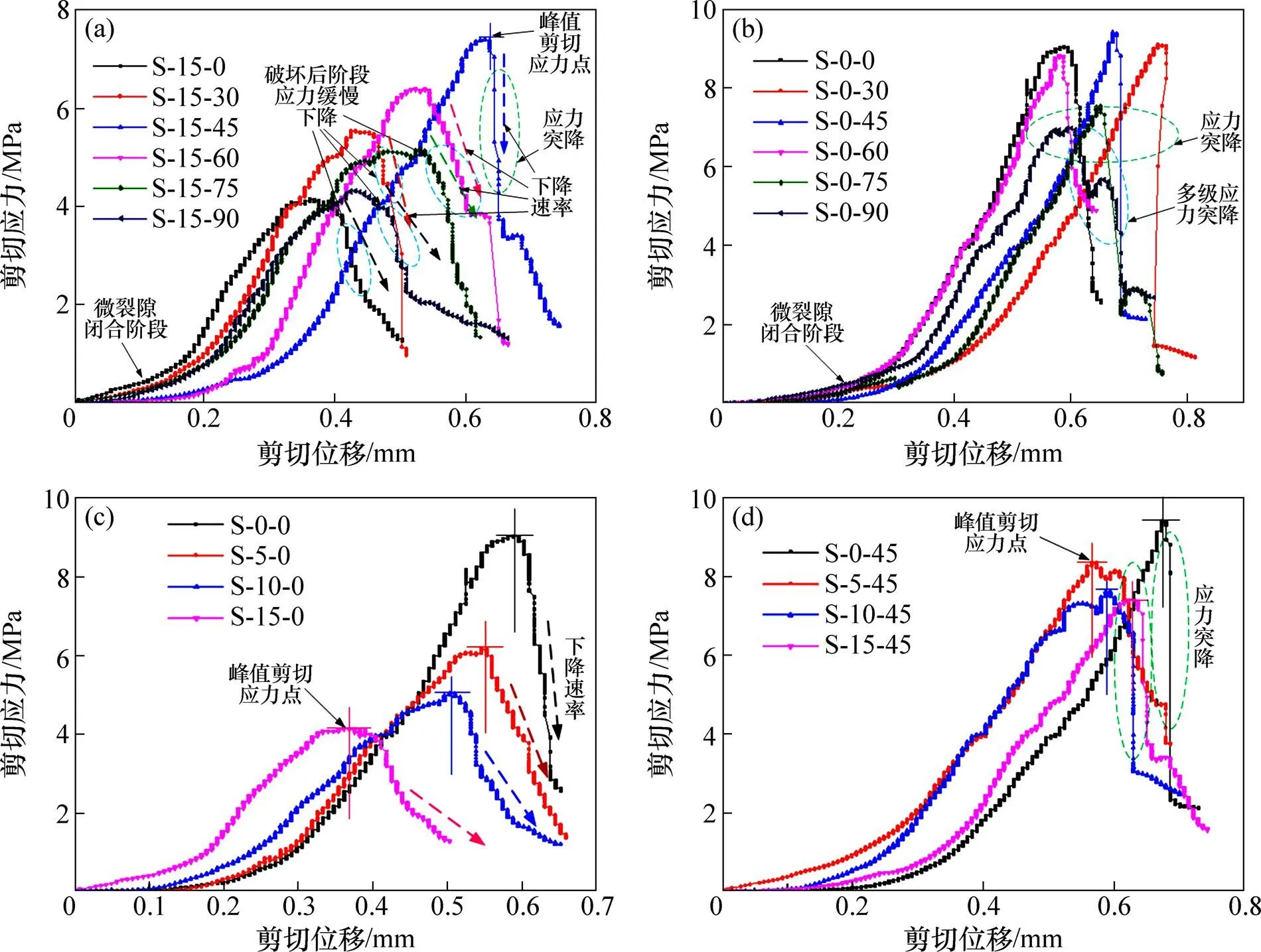
(a) 重叠长度为15 mm时，不同倾角试样剪切应力−位移曲线；(b) 重叠长度为0 mm时，不同倾角试样剪切应力−位移曲线；(c) 节理倾角为0°时，不同重叠度剪切应力−位移曲线；(d) 节理倾角为45°时，不同重叠度剪切应力−位移曲线

(a) S-5-0；(b) S-10-0

观察不同重叠度试样的峰值剪切强度分布(图10)明显发现其点分布看似杂乱无章，但也呈现一定的规律，重叠长度为0 mm的试样整体上位于右上角、重叠长度为15 mm的试样位于左下角，峰值剪切强度及峰值位移都随重叠度的增大呈现整体上减小的趋势。

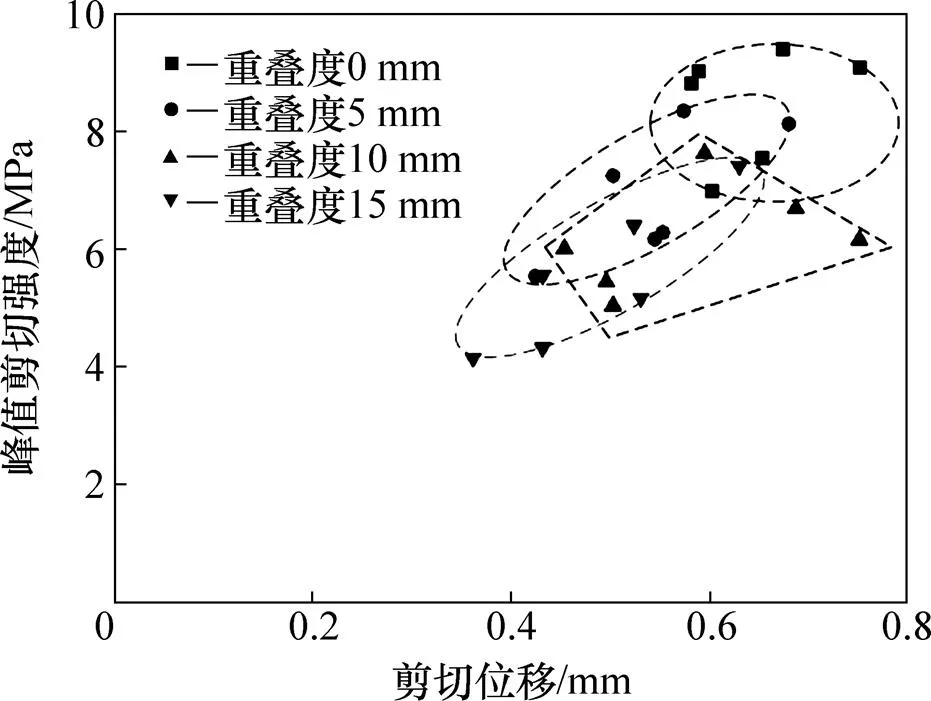
图10 试样的峰值剪切强度−位移分布图

5 结论

1) 根据破坏面与剪切应力面、节理面之间的关系，试样破坏模式可分为4种，倾角对试样破坏模式起决定性作用：0°倾角为共面剪切破坏；30°和60°倾角为沿节理面剪切破坏；45°倾角为类完整型剪切破坏；75°和90°倾角为沿剪切应力面剪切破坏。重叠度影响试样裂隙的发育，但不改变试样的破坏模式。

2) 试样峰值剪切强度随倾角增加先增大后减小且在45°取得最大值；随着节理重叠度的增大，峰值剪切强度逐渐减小。节理重叠度越大(峰值剪切强度越小)，峰值剪切强度随倾角变化幅度越大；剪切峰值强度对倾角因素更敏感，但随着节理重叠度的不断减小重叠度对峰值剪切强度的影响不断增强。

3) 剪切应力−位移全过程曲线结合声发射计数特征从试样受载直到破坏可划分为4个典型的阶段：微裂隙闭合阶段、弹性阶段、裂隙扩展直到破裂阶段和破裂后阶段。不同倾角试样的剪切应力−位移曲线差异主要体现在破裂后阶段，相同破坏模式的试样曲线形态相似。

4) 不同倾角试样声发射计数变化规律与试样破坏模式相适应，其验证了节理倾角对破坏模式的决定作用。不同重叠度试样声发射计数随应力−位移曲线变化形态相似，但声发射计数峰值随重叠度的增大逐渐减小。

[1] 车法星, 黎立云, 刘大安. 类岩材料多裂纹体断裂破坏试验及有限元分析[J]. 岩石力学与工程学报, 2000, 19(3): 295−298. CHE Faxing, LI Liyun, LIU Daan. Fracture experiments and finite element analysis for multi-cracks body of rock-like material[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 295−298.

[2] WANG Min, CAO Ping, WAN Wen, et al. Crack growth analysis for rock-like materials with ordered multiple pre-cracks under biaxial compression[J]. Journal of Central South University, 2017, 24(4): 866−874.

[3] YANG Xuxu, JING Hongwen, TANG Chunan, et al. Effect of parallel joint interaction on mechanical behavior of jointed rock mass models[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 92: 40−53.

[4] 王佩新, 曹平, 蒲成志, 等. 单压下节理密度及倾角对类岩石试件强度及变形的影响[J]. 工程科学学报, 2017, 39(4): 494−501. WANG Peixin, CAO Ping, PU Chengzhi, et al. Effect of the density and inclination of joints on the strength and deformation properties of rock-like specimens under uniaxial compression[J]. Chinese Journal of Engineering, 2017, 39(4): 494−501.

[5] PRUDENCIO M, VAN SINT JAN M. Strength and failure modes of rock mass models with non-persistent joints[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 890−902.

[6] CAO Rihong, CAO Ping, FAN Xiang, et al. An experimental and numerical study on mechanical behavior of ubiquitous-joint brittle rock-like specimens under uniaxial compression[J]. Rock Mechanics Rock Engineering, 2016, 49(11): 4319−4338.

[7] CORDING E, JAMIL M. Slide geometries on rock slopes and walls[C]//Fourth South American Congress on Rock Mechanics. Santiago, 1997: 199−221.

[8] 杨圣奇, 戴永浩, 韩立军, 等. 断续预制裂隙脆性大理岩变形破坏特性单轴压缩试验研究[J]. 岩石力学与工程学报, 2009, 28(12): 2391−2404. YANG Shengqi, DAI Yonghao, HAN Lijun, et al. Uniaxial compression experimental research on deformation and failure properties of brittle marble specimen with pre-existing fissures[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2391−2404.

[9] YANG Shengqi, TIAN Wenling, HUANG Yanhua, et al. An experimental and numerical study on cracking behavior of brittle sandstone containing two non-coplanar fissures under uniaxial compression[J]. Rock Mechanics & Rock Engineering, 2016, 49(4): 1497−1515.

[10] YANG S Q, LIU X R, JING H W. Experimental investigation on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 63(5): 82−92.

[11] 陈新, 李东威, 王莉贤, 等. 单轴压缩下节理间距和倾角对岩体模拟试件强度和变形的影响研究[J]. 岩土工程学报, 2014, 36(12): 2236−2245. CHEN Xin, LI Dongwei, WANG Lixian, et al. Experimental study on effect of spacing and inclination angle of joints on strength and deformation properties of rock masses under uniaxial Compression[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2236−2245.

[12] 陈新, 廖志红, 李德建. 节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J]. 岩石力学与工程学报, 2011, 30(4): 781−789. CHEN Xin, LIAO Zhihong, LI Dejian. Experimental study of effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 781−789.

[13] 蒲成志, 曹平, 赵延林, 等. 单轴压缩下多裂隙类岩石材料强度试验与数值分析[J]. 岩土力学, 2010, 31(11): 3661−3666. PU Chengzhi, CAO Ping, ZHAO Yanlin, et al. The numerical analysis and strength experiment of rock-like material with multi-fissures under uniaxial compression[J]. Rock and Soil Mechanics, 2010, 31(11): 3661−3666.

[14] FAN X, KULATILAKE P H S W, CHEN X. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: a particle mechanics approach[J]. Engineering Geology, 2015, 190: 17−32.

[15] WASANTHA P L P, RANJITH P G, VIETE D R, et al. Influence of the geometry of partially spanning joints on the uniaxial compressive strength of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 50(2): 140−146.

[16] SARFARAZI V, GHAZVINIAN A, SCHUBERT W, et al. Numerical simulation of the process of fracture of echelon rock joints[J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1355−1371.

[17] RAO Qiuhua, SUN Zongqi, STEPHANSSON O, et al. Shear fracture (Mode II) of brittle rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 355−375.

[18] 李庶林, 尹贤刚, 王泳嘉, 等. 单轴受压岩石破坏全过程声发射特征研究[J]. 岩石力学与工程学报, 2004, 23(15): 2499−2503. LI Shulin, YIN Xiangang, WANG Yongjia, et al. Study of acoustic emission signature of the rupture process of unixial compressed rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2499−2503.

(编辑 杨幼平)

Influence of parallel joint interaction on mechanical behavior of jointed rock mass

WANG Fei, CAO Ping, CAO Rihong, GAO Qingpeng, XIONG Xinguang, WANG Zhu

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

In order to investigate the influence of joint interaction on the mechanical behavior of rock mass, the compression shear test loading on the parallel jointed specimens was carried out, and the acoustic emission system was used to monitor the loading process. The results show that: 1) Under compressive-shear loading, the failure mode of the jointed specimen can be classified into four types: coplanar shear failure; shear failure along the joint plane; shear failure along the shear stress plane; similar integrity shear failure. The inclination angle has a decisive effect on the failure mode of the specimen, and the joint overlap affects the growth of the specimens’ crack. 2) The peak of shear strength firstly increases and then decreases with the increase of the inclination angle, and reaches the maximum at 45°. The peak of shear strength decreases with the increase of the joint overlap. The peak of shear strength is more sensitive to the joint inclination. 3) The difference of shear stress-displacement curve for different inclination is mainly reflected in the post-rupture stage; the variation of the acoustic emission count for different joint inclination samples corresponds to the failure mode of specimen. The stress−displacement curves of different overlapping specimens are similar, and the change of acoustic emission count is similar, but the peak value of the acoustic emission count decreases with the increase of the joint overlap.

joint interaction; joint overlap; compression-shear test; mechanical behavior; acoustic emission(AE)

10.11817/j.issn.1672−7207.2018.10.017

TU452

A

1672−7207(2018)10−2498−10

2017−10−12；

2017−12−21

国家自然科学基金资助项目(11772358)；中南大学中央高校基本科研业务费专项资金资助项目(2017zzts164) (Project(11772358) supported by the National Natural Science Foundation of China; Project(2017zzts164) supported by the Fundamental Research Funds for the Central Universities)

曹平，教授，从事岩石力学研究；E-mail：pcao_csu@sina.com