HSMA：面向物联网异构数据的模式分层匹配算法

郭 帅 郭忠文 仇志金

(中国海洋大学信息科学与工程学院 山东青岛 266100) (guoshuaiouc@163.com)

据物联网行业统计数据显示，2014年中国物联网产业规模达到5 800亿元，同比增长18.46%.2015 年全球物联网市场规模达到 624 亿美元，同比增长 29%.到 2018 年全球物联网设备市场规模有望达到 1 036 亿美元，2019 年新增的物联网设备接入量将从2015 年的16.91 亿台增长到30.54 亿台[1].随着物联网的快速发展以及物联网平台的逐步成熟，无处不在的末端设备和设施，如智能传感器、移动终端等通过物联网连接在一起，万物互联已经成为必然趋势.随之兴起的物联网技术被广泛应用到各个领域，产生了海量的异构数据.Mccrory[2]在2010年提出了“数据引力”的概念，将数据、软件应用、接口服务等比作星体，含有各自的质量和密度，数据质量不断地增加并且远大于其他“星体”，而其他“星体”都将被巨大的引力吸引过来并以数据“星体”为中心.由此可见，对于物联网异构数据，其处理技术的发展将会直接影响整个物联网技术的发展和进步.目前大部分的异构数据都是独立、分散地存储于各个地区，形成了大量信息孤岛，由结构化数据(如关系型数据库)、半结构化数据(如XML，HTML)和非结构化数据(如NoSQL数据库、图片、视频)等多种形式组成，如何通过“2次采集”将这些信息孤岛互联起来受到人们的关注.

模式匹配技术在数据互联过程中发挥着巨大的作用[3]，尽管目前对物联网异构数据可以通过制定统一数据接口标准的方式进行互联，但在实际应用中却很难实现，因为对于已经存在的海量数据存储模式的改造成本是巨大的，可以说数据异构的问题是不可避免的，数据模式匹配技术为解决以上问题提供了一个良好的解决方案.模式匹配是一个构建源模式和目标模式中元素间映射关系的过程，而传统的模式匹配操作大多都是由IT技术人员手工完成，随着数据规模的扩大以及模式复杂度的提升，手工匹配会耗费巨大的人力物力，并且容易破坏数据的完整性和准确性.目前已有的研究成果利用元素自身信息、语义信息、数据实例信息和结构信息来挖掘模式正确的元素映射关系.在之前的工作中，我们构建了一个面向物联网的异构数据转换模型，实现快速高效的物联网异构数据互联，然而在互联过程中模式匹配过程的人工参与度过高，匹配效率低下.为了解决该问题，我们首先分析了物联网异构数据的特征，即时间序列特征.并以此为切入点，通过解析时间序列数据来对物联网异构数据进行分类识别，为自动模式匹配提供了可能.基于以上研究成果，本文提出了一种面向物联网异构数据的模式分层匹配算法(hierarchical schema matching algorithm， HSMA)，该算法基于数据模式的实例信息，通过3层映射匹配：特征分类匹配、关系特征聚类匹配和混合元素匹配，实现了物联网异构数据的模式自动匹配，减小了复杂模式下元素间匹配空间，提高了自动匹配的效率和准确度.

1 相关研究及问题分析

1.1 相关研究

目前比较典型且已经广泛应用的匹配算法有Auto-match,Clio,COMA,iMAP,Cupid,LSD,GLUE等.Cupid[4]利用属性名称、数据类型等模式信息计算属性之间的语义相似性，将语义相似度和结构相似度结合起来进行匹配.COMA[5]利用多种匹配器协同工作，通过过滤、筛选来提高匹配结果的准确率和效率.LSD[6]应用机器学习算法实现匹配并且自动整合匹配结果，可以很好地发现1∶1和1∶n的匹配.基于数据实例信息的模式匹配的iMAP[7]方法是一种综合利用模式中多种类型的信息同时得到模式间的简单和复杂映射关系的方法，可以很好地发现1∶1和1∶n的匹配.

1.2 问题分析

文献[8]提出了一种基于实体分类的数据库模式匹配方法，根据数据实例信息的语义信息进行特征提取，运用朴素贝叶斯算法对特征进行分类，最后对子模式进行相应的模式匹配.由于物联网数据的海量性和异构性，无论数据库设计得多么规范化，但其属性名称和意义的定义因人而异，单一地以属性名等语义信息进行模糊分类的方式是不可取的，因为这种分类仅仅基于人为理解而非源数据的本质特征.文献[9]利用数据的概率分布统计特征，从另一个角度对数据特征进行提取，利用BP神经网络算法提高了模式匹配效率和准确度.然而该算法针对的仅仅是1:1列之间的匹配，不适用于复杂模式匹配.随着数据规模不断增大，匹配空间和匹配次数也会急剧增加，导致匹配效率低下.与文献[8-9]的算法相比，本文提出的HSMA算法能够较好地解决在现实应用中自动获取解析数据源模式信息困难的问题，通过解析海量异构的原始数据，按照物联网数据的时间序列性特征将解析的特征进行分类，从而代表数据源的模式特征；其次，HSMA算法中的关系特征聚类方法具有一定创新性，尤其对物联网传感数据的特征聚类有良好的效果，消除了数据集数据间不同数据类型差异的影响；最后，HSMA运用分层的方法逐步缩小匹配空间，减少匹配次数，提高了匹配的效率.

2 HSMA算法

为了实现物联网异构数据(结构化数据)的模式匹配的智能化，我们设计了一种模式分层匹配算法HSMA.对于输入的一个未知源数据，我们首先根据时间序列特征和数据类型特征对其所有的数据集进行分类，获得子模式集合.与此同时，通过之前的研究成果IFRAT算法，获取未知数据源领域特征信息，根据领域的不同初始化相应的领域标准集合以及标准化数据库进行关系特征聚类匹配，建立各类中源数据集合和目标数据库之间的映射关系(第1层匹配)；然后依据所提取的数据集特征，运用机器学习算法，对每个子模式中的数据集进行聚类，进一步缩小匹配空间和范围，对聚类结果与相应的标准集合数据集进行相似度计算，建立匹配映射(第2层匹配)；最后将相匹配的聚类中的元素混合并进行相似度计算(第3层匹配)，产生源数据与目标数据库之间的模式匹配结果.通过以上3层匹配，HSMA逐步缩小匹配空间，降低了匹配次数，从而提高匹配效率.HSMA算法的整体架构如图1所示：

Fig. 1 Architecture of HSMA图1 HSMA算法架构

2.1 源数据标准化

每个数据集中存在多种类型数据，以往的模式匹配算法都是对同一个数据集中不同类型元素进行单独处理，处理方法多样，虽然能够保留单一元素特征，但是却破坏了不同类型元素间的关联关系，失去了整个数据集的特征.因此，针对数据集中常见的数据格式(如数值、字符、日期等)，需要寻找一个统一的数据处理方式以保证其特征的完整性.首先，我们将每个结构化数据集都看作是一个存在行列关系的2维矩阵，矩阵中的相邻行元素的差值变化结果作为新矩阵的行，我们将新的矩阵成为关系矩阵.差值变化结果用-，0，+表示，通过该方法，我们用关系值代替了原来的内容值，将不同类型的数据转化为同一标准，最终得到关系矩阵.关系矩阵作为数据集的一个标准化形式，能够更好地被用于数据集的特征挖掘.

为了更好地对HSMA算法进行理解，我们对本文中所用到的一些名词进行定义.

定义1. 关系矩阵.对于任意常见的结构化数据Dm×n，都可以通过相邻行做差的方法，差值结果用-，0，+这3种符号表示，我们将这样的矩阵定义为关系矩阵，用M表示.

定义2. 关系键对.关系矩阵M的每一行中元素两两组合所形成的键对.

定义3. 特征列.对于关系矩阵M的任意一列，当且仅当同时满足2个条件：1)该列元素的数值类型为日期类型或可以转化成日期类型的其他数据类型；2)该列中的元素“+”或元素“-”的出现频率大于阈值θ(我们取θ=90%)，这样的列被称作时间序列特征列.如果仅满足条件2，则该列被称为主特征列.

定义4. 时间序列数据.物联网传感器产生的原始数据，按照时间顺序以结构化的形式存储，这样的数据集合被称为时间序列数据.

2.2 3层映射匹配

本节对HSMA的分层匹配算法进行了详细的描述，共分为3层：第1层为特征分类匹配(时间序列特征和数据类型特征)；第2层为关系特征聚类匹配；第3层为混合元素匹配.基于分层的思想，我们将复杂的异构数据模式匹配过程分割成3步，逐步缩小其匹配空间.对于每一步的匹配，都是基于物联网异构数据特性，比较源数据与标准数据间的相似性，构建映射关系，最终实现物联网异构数据的模式自动匹配.

2.2.1 特征分类匹配

HSMA算法在特征分类匹配过程中提供2种分类方法：

1) 时间序列特征分类

时间序列是物联网异构数据的标志性特征，可以被用来进行物联网异构数据分类.首先我们将物联网异构数据的按时间序列特性分为3类：

① 时间序列数据类P.所有包含时间序列特征列的数据集属于时间序列数据类(如传感网传感数据).

② 时间序列属性类Q.包含主特征列的数据集归于时间序列数据属性类(如传感网监测对象元数据)，如描述时间序列属性的相关信息.

③ 非时间序列类R.包含与时间序列无关的数据集，一般由许多相关辅助信息组成.

HSMA算法将物联网异构数据按照时间序列特征分类，最后得到数据分类集合{时间序列数据类，时间序列属性类，非时间序列类}，其具体的分类算法如算法1所示：

算法1. 时间序列特征分类算法.

输入：物联网异构数据集合X={x1,x2,…,xn}(结构化数据)；

输出：时间序列特征类集合{P，Q，R}.

① 获取物联网异构数据集合(结构化数据)，X={x1,x2,…,xn};

② 对X中所有数据集xi进行数据标准化，得到与X相对应的关系矩阵集合Y={M1,M2,…,Mn};

③ ∀xi∈X，遍历xi的每一列，依据时间序列特征对xi进行分类;

④ for eachxi∈Xdo

⑤ for eachcol属于Mi的列集合 do

⑥n=Column_num(Mi);

⑧ ifθ≥90% then

⑨ ifcol∈Type.datethen

⑩xi∈P;

2) 数据类型特征分类

物联网异构数据中，不同领域的源数据集合具有不同的数据类型分布特征，依据该特征对物联网异构数据分类.数据类型按照物联网异构数据的常见类型被分为5类:数值型(value)、字符类型(char)、时间类型(date)、字符-数值类型(char-value)、字符-时间类型(char-date)，考虑在复杂模式匹配下，相同的数据可能被赋予不同的数据类型，数据类型间的相互转换会导致其分布特征偏离，因此将字符串-数值等可以相互间进行转换的情况列入数据类型特征.利用各个数据类型出现的频率值，构建一个5维的特征向量，然后依据特征向量对物联网异构数据进行特征分类：

① 时间主导类E.由于时间类型的特殊性，只要包含时间类型的数据集都属于时间主导类.

② 数值主导类F.数值类型(如int,long,float,double等)占比重大的数据集属于数值主导类.

③ 字符主导类G.字符类型(如char,varchar,nvarchar等)占比重大的数据集属于字符导类.

HSMA算法将物联网异构数据按照数据类型特征分类，最后得到数据分类集合{E，F，G}，其具体的分类过程如算法2所示：

算法2. 数据类型特征分类算法.

输入：物联网异构数据集合X={x1,x2…,xn}(结构化数据)；

输出：数据类型特征类集合{E，F，G}.

① 获取物联网异构数据集合(结构化数据)，X={x1,x2…,xn};

② 对X中所有数据集xi进行数据结构标准化;

③ ∀xi∈X，遍历xi的每一列，依据数据类型分布特征构建xi的特征向量vi，得到X相对应的特征矩阵V=(v1,v2,…,vn);

④ for eachxi∈Xdo

⑤ for eachcol∈xido

⑥ 统计过程①中各个数据类型发生次数;

⑦ end for

⑧ 构建数据类型特征向量vi;

⑨n=Column_num(xi);

2.2.2 关系特征聚类匹配

通过2.2.1节中的特征分类匹配，对源数据S和标准化数据库T中的数据分别进行时间序列特征分类和数据类型特征分类，得到的结果集合统称为Scla和Tcla.在本节，我们采用SOM聚类方法对Scla和Tcla中的数据集进行归类，进一步缩小匹配空间.在聚类过程中，我们采用关系矩阵M作为数据集的特征矩阵，因为关系矩阵M具有以下特点：1)M可以将数据集中不同类型的数据转换成统一的符号表示；2)M可以保留元素间的相互关系，而传统的匹配方法忽略了这一点；3)M解决了复杂模式匹配下元素排列顺序多变的问题，更好地表现数据集特征.关系矩阵M中，每一行中所有项两两组合形成关系键对，HSMA算法通过对数据集进行行遍历，提取数据集关系键对的频率分布特征，作为该数据集的特征向量vi，基于得到的特征向量进行聚类匹配.详细过程如算法3所示：

算法3. 关系特征聚类匹配算法.

输入：Scla，Tcla;

输出：Scla和Tcla的聚类集合.

① 获取Scla和Tcla中的分类集合：Scla或Tcla={Classification1，Classification2，Classi-fication3};

②dataset∈{E,F,G};

③ for eachClassification∈Sclado

④ for eachds∈datasetdo

⑤ds→M;

⑥ for eachrow属于M的行集合 do

⑦ 关系键Key←{(-，-),(-，0),(-，+),(0，0),(0，+),(+，+)};

⑧ 统计每种关系键Key出现的次数;

⑨ end for

⑩n←统计所有关系键Key出现的总次数；

在本节，我们基于关系矩阵中提取的特征向量，对Scla中的所有数据集进行聚类，得到聚类集合D={d1,d2,…,dl}，通过计算欧氏距离，确定Tcla中的每一个数据集在Scla中最相似的聚类集合，从而进一步缩小匹配空间.我们假设并认定S中的每一个聚类对应T中唯一的数据集，即数据集之间只存在1∶n的关系.

2.2.3 混合元素匹配

基于2.2.2节得到的聚类集合D.∀di∈D，我们将di中的所有元素混合在一起，采用文献[10]的算法对于单一元素进行聚类匹配，该算法能够快速有效地发现聚类中心，能够在短时间内完成聚类过程且过程精简，最终得到匹配结果集合R={r1,r2,…,rl}.考虑到现实情况的复杂性，我们很难做到元素1∶1的精准匹配，所以∀ri∈R，我们规定ri中只包含1个标准化数据元素和φ个源数据的元素(这里的φ人为设定，本文选取φ=1,2,3)，这φ个源数据的元素作为最相似的元素被推荐用户，具体如算法4所示：

算法4. 混合元素匹配算法

输入：聚类集合D←{d1,d2,…,dl};

输出：匹配结果集合R←{r1,r2,…,rl}.

① 获取聚类集合：D←{d1,d2,…,dl};

② for eachdi∈Ddo

③ 运用文献[10]算法进行匹配;

④ 设定φ的数值;

⑤ri←di的匹配结果;

⑥ end for

⑦ return匹配结果集合R←{r1,r2,…,rl}.

3 实验验证及结果分析

3.1 数据选取

为了证明HSMA的可行性和有效性，我们选取工业物联网家电产品测试领域的家用空调性能测试中13个不同厂家的30个数据库作为源数据，将基于国际标准IEEE 1851的空调测试数据库作为标准化数据库(采用Oracle)，数据详细信息如表1所示:

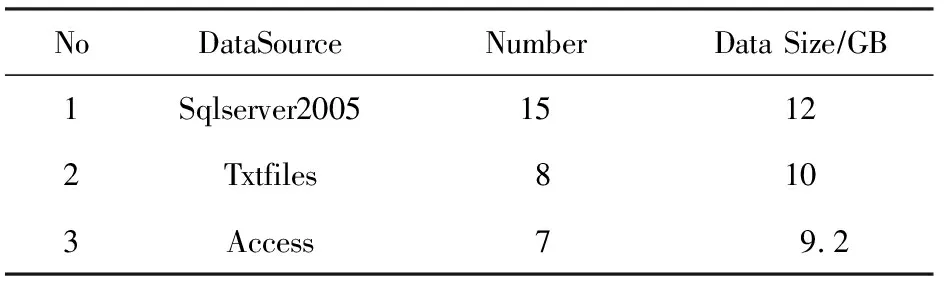
Table 1 Performance Test Data of Residential Air Conditioner

我们认为一般情况下存在2种常见的异构形式：行列转换和拆分.

1) 行列转换.不是完全属于同一列的内容被列入同一列中，为了消除结构不同对匹配造成的影响，我们需要对这一类型的列进行逻辑行转换，同时记录相应映射关系，如图2所示：

Fig. 2 Row-column transforming of IoT heterogeneous data图2 物联网异构数据行列转换

2) 拆分.通常情况下列的合并要么是字符串由特殊字符隔开，要么布尔型直接合并，所以找到合并字段进行逻辑拆分，同时记录相应的映射关系，如图3所示：

Fig. 3 Logic splitting of IoT heterogeneous data图3 物联网异构数据逻辑拆分

3.2 算法对比

我们采用不同的基于数据实例和数据库模式信息的模式匹配算法与HSMA算法进行对比，详细的对比信息如表2所示：

1) SMEC[8].通过朴素贝叶斯学习将实体分为不同的类，以同样的类来匹配子模式之间的模式元素.

2) SMDD[9].基于神经网络的模式匹配算法，通过分析模式元素所包含的数据实例的分布规律，自动完成模式匹配.

3) iMAP[7].一种综合利用模式中多种类型的信息同时得到模式间的简单和复杂映射关系的方法，在得到匹配关系的同时保存对每个匹配关系的判断过程，当用户对最终结果进行调整时，向用户提供保存的判断过程作为用户进行调整的依据.

Table 2 Comparison of Different Algorithms表2 不同算法之间比较

3.3 实测结果

为了评估HSMA的匹配质量，我们采用3个通用指标[11]进行评估：

1) 查准率(Precision).匹配结果中正确匹配结果的比率.

(1)

其中,T为正确识别的匹配结果，P为匹配方法返回的匹配结果，F为错误的匹配.

2) 查全率(Recall).匹配结果中正确匹配结果占实际匹配结果的比率.

(2)

其中，R为手工匹配结果.

3)F1_measure.能够全面评价匹配质量的统计量.

(3)

3.3.1 HSMA算法自测

1) HSMA算法的匹配质量受到参数φ选取的影响.通过对φ设定不同的值，分析比较其查准率、查全率和F1-measure，结果如图4所示.与φ=1相比，当φ>1时，查全率、查准率和全面性都有提高，因为HSMA算法无法保证精准的1∶1匹配，模式的异构性导致存在多个相近的相似度结果.但并不是φ值越大越好，φ的增大会导致匹配干扰项增加，降低匹配质量，当φ=3时，可以看出其匹配质量大于φ=1但小于φ=2.

Fig. 4 Matching quality of HSMA under different φ图4 在不同的φ下HSMA的匹配质量

2) HSMA算法的匹配质量受到输入数据库数量的影响.输入数据库的个数会直接影响关系特征聚类的效果，充足的数据会使数据特征更加明显.如图5所示，对于不同的φ值，当输入数据库数量在(0，15)范围时，其匹配质量随着输入数据库个数的增加而不断提高且变化较为明显；但当输入数据库数量大于15后，匹配质量增长缓慢.

Fig. 5 Matching quality of HSMA with the increasing number of input databases图5 随着输入数据库数量的增加HSMA的匹配质量

Fig. 6 Matching time of HSMA图6 HSMA需要的匹配时间

3) HSMA算法的时间效率受参数φ选取的影响.图6比较了在φ值的不同情况下源数据个数对HSMA算法时间效率的影响.如图6所示，φ越大，HSMA算法所用的匹配时间就越大，因为φ值的增加导致在混合元素匹配过程中匹配次数的增多，提高了时间复杂度；当φ值固定时，采用时间序列特征分类的HSMA算法的匹配时间低于采用数据类型特征分类的HSMA算法.

4) HSMA算法的时间效率受特征分类的影响.我们随机选取15个数据源作为HSMA算法的输入，分别采用无分类、时间序列特征分类和数据类型特征分类并且设定不同的值，分析比较其每一层匹配所用时间，结果如图7所示.φ的选取仅仅会影响混合元素匹配的匹配时间，φ值越大混合元素匹配过程所用的时间就越多；当φ值固定时，采用时间序列分类的HSMA算法的匹配时间相对较小.

Fig. 7 Hierarchical matching time of HSMA图7 HSMA的每一层匹配时间

3.3.2 算法性能对比

由3.3.1节可得，当选取φ=2，采用时间序列特征分类的HSMA算法的性能最高，因此将其与3.2节中各个模式匹配算法进行比较.我们选取了30个异构数据库作为HSMA的输入，比较所得结果如图8所示.如图8(a)所示，HSMA算法的匹配质量与其他算法相比较高，其中源数据库的异构性和模式信息的不完整导致SMEC效率最差.如图8(b)所示，由于HSMA算法采用预处理以及多次聚类，导致其所用时间明显高于其他算法.

Fig. 8 Performance comparison of HSMA with other algorithms图8 HSMA算法与其他算法的性能比较

4 总结和未来工作

我们设计了一种模式分层匹配算法HSMA，对于输入的一个未知源数据，根据领域的不同初始化相应的领域标准集合以及标准化数据库进行特征分类匹配，建立各分类中源数据集合和标准数据库数据集合的映射关系；然后提取源数据集和目标数据库表中的关系特征，运用SOM聚类算法，对每一个子模式中的数据集进行聚类，对聚类结果与相应的标准数据库数据集进行相似度计算，建立匹配映射；最后将匹配结果集合中的混合元素进行相似度计算，进行单一元素匹配.通过以上3层匹配，HSMA算法逐步缩小匹配空间，降低了匹配次数，从而提高匹配质量和效率.

由于在关系特征聚类匹配及混合元素匹配的过程中，聚类算法的好坏直接决定了最后的匹配质量和总体的匹配时间，聚类虽然能够缩小匹配空间，但同时有可能带来匹配错误，导致相关元素并不在同一个类中.未来会尝试使用不同的机器学习算法对HSMA算法进行改进，并且寻找最好的组合模式来提高聚类的效果.此外本文在实验验证环节采用iMAP,SMDD等经典算法与HSMA算法进行对比，提高了对比结果的可靠性，但是这些算法偏于老旧，下一步将采用近几年的新算法进行比较，以验证HSMA算法的先进性.