空间遥感相机挠性支撑扫描装置测角精度标定方法
2018-11-12迟冬南徐丽娜赵鑫张秀茜贾慧丽
迟冬南 徐丽娜 赵鑫 张秀茜 贾慧丽
空间遥感相机挠性支撑扫描装置测角精度标定方法
迟冬南 徐丽娜 赵鑫 张秀茜 贾慧丽
(北京空间机电研究所,北京 100094)
针对空间遥感相机挠性支撑扫描系统的测角精度标定问题,利用高精度经纬仪测量扫描镜摆动过程中采集的角度误差数据,研究了适用于空间复杂环境的分段误差补偿方法。利用光电自准直仪对扫描镜的零位进行监测,以解决经纬仪随时间、环境引起的零位漂移。根据高轨应用需求,分析了分段误差补偿法的必要性。将获得角度误差引入补偿系统,采用分段误差补偿法对测角电路进行标定。将测试结果与谐波误差补偿法标定结果对比,验证了分段误差补偿后系统的测角精度能够满足系统性能指标要求。最终确定了分段误差补偿法在空间遥感相机有限角度扫描系统高测角精度实现过程中的有效性。
扫描装置 测角误差测量 标定方法 空间相机
0 引言
随着空间遥感技术的发展,对空间相机的视场范围、成像品质等要求越来越高。虽然受到大面阵探测器水平及探测器拼接技术等约束,在未来一段时间内,扫描式空间相机仍具有广阔的应用空间[1-2]。扫描式空间相机利用扫描镜的摆扫或旋转扫描,完成有效视场的成像。为了获得准确的位置,需要通过高精度测角来确定地物目标的绝对位置,因此,空间相机扫描系统的测角精度直接关系到遥感图像的品质。
为了满足高精度的测角需求,需要根据空间相机的运行轨道等条件,在感应同步器、光电码盘及旋转变压器等几种测角元件中筛选。本文针对高轨道空间相机,选取感应同步器作为高精度测角元件,将扫描镜的角位置反馈到扫描系统中。
感应同步器的测角误差主要包括长周期一次谐波、短周期一次谐波和短周期二次谐波[3]。为了完成测角误差的标定,前提是需要建立测角误差模型。通过测量角度误差数据,结合测角误差模型进行角度补偿,进而提高系统的测角精度[4-5]。
误差模型可以采用传统的模型机理分析进行构建,也可以利用现代智能算法予以实现。文献[6]利用实测的误差数据,基于傅里叶变换分析,通过离线数据辨识的方法构建零位误差和细分误差补偿模型,使得测角系统的全误差达到±2,神经网络等智能算法的引入使得系统的零位误差达到±1[7-8]。
为了提高误差模型的准确性,在模型参数辨识过程中采用实测数据进行补偿与迭代。因此,经纬仪、光电自准直仪等高精度测角装置成为误差测量的基准[9-10]。由于测角装置的自身属性,针对测量范围小与测试精度之间的矛盾关系,在解决测量范围小的问题中,采用双经纬仪的非接触式检测方法对扫描反射镜的定位精度进行检测[11];为了消除了人工读数过程中的测量误差,提高检测结果的准确性,引入自动采集系统获取自准直仪数据,并利用最小二乘法辨识误差模型系数,有效减小检测数据的残差,测角误差得以充分补偿[12]。
获得测角误差后,需要将其引入到补偿系统实施测角电路的标定。由于误差是系统各环节综合作用的结果,因此,误差补偿是针对整个系统进行的。在实际系统中,感应同步器的安装误差、误差模型的非线性等也都会对扫描系统的测角精度造成不同程度的影响。因此,控制感应同步器的安装误差[13]、误差非线性模型线性化等也需要在设计中充分考虑。
本文结合空间遥感相机扫描系统的工作方式及特点,探索了适用的角位置测试方法,阐述了误差标定方案的可实现性和有效性,并通过测试试验对提出的标定方案进行了验证。
1 扫描系统角位置误差测量方法
扫描系统采用摆扫方式,有效摆扫范围为±5°,最大摆扫角度小于±6°。在设计扫描机构装置时,为了实现有效摆扫范围的同时保证高精度测角精度和控制精度的要求,对各部分元件选取进行了充分论证。考虑空间复杂的应用环境与高精度的测角要求,选择感应同步器作为角位置传感器。目前,感应同步器的精度可以达到0.1,但受空间限制,最终选择测角精度为1的绝对圆感应同步器。
本项目的关键问题在于扫描系统转轴两端采用挠性枢轴支撑,与轴承支撑相比,整个轴系的同轴度较差,因此,对测角精度将造成不利影响。针对挠性枢轴支撑扫描系统的高精度测角问题,需要测量扫描镜的角位置误差,并利用角位置误差对测角电路进行补偿。角位置误差测量和测角补偿两个过程相互迭代,使扫描系统的测角精度逐渐收敛,直至满足系统测角精度±2″的要求。
为了保证空间扫描系统的测角精度的要求,本项目采用高精度经纬仪完成角位置误差和系统测角精度的测量。经纬仪的测量精度为0.5″,图1为测试系统组成示意。
扫描镜旋转至某个位置,经纬仪和感应同步器测角电路均能读到其空间角度1和2。假定经纬仪的读数即为准确的空间角位置,则经纬仪读数与感应同步器测角电路的差值即为扫描镜的角位置误差。将测角系统误差引入补偿系统,补偿后的测角电路重新参与误差测试。误差测量与误差补偿过程相互迭代,最终使整个扫描系统的测角精度达到指标要求。根据指标要求,此误差应小于2。
利用经纬仪进行误差测试需要考虑以下两个方面影响:1)经纬仪需要人工瞄准,因此,会引入读数误差;2)经纬仪本身会随时间和环境变化产生漂移。由此可知,采用经纬仪进行测角误差来源包括瞄准误差和经纬仪的角位置漂移。下面分别分析瞄准误差和经纬仪漂移对测角精度的影响。
(1)瞄准误差[14]
瞄准误差是在观测过程中引入的随机误差。为了尽量减小瞄准误差,将经纬仪调平,并反复瞄准同一个目标点10次,每次将经纬仪转动后重新瞄准,记下每次观测的读数数据x(=1,2,3,…,10)。计算经纬仪瞄准误差
经过计算,测试过程中产生的瞄准误差能够达到优于0.1。
(2)经纬仪漂移
为了监测经纬仪在误差测量过程中的漂移情况,引入光电自准直仪对扫描镜的零位进行监测。光电自准直仪在±1 000内的精度可达到0.2,因此,配合基准反射镜,能够反映扫描零位的角位置漂移。当零位角度偏移小于0.5时,可认为测试数据有效,否则,需要重新测试。
2 测角误差分段补偿方法
360极绝对圆感应同步器的测量范围为360°,节距为2°,通过粗精通道的配合实现绝对角度测量。感应同步器的误差包括以360°为周期的长周期零位误差、以2°为周期的短周期零位误差与每2°范围内的细分误差。根据扫描系统的转动范围,误差标定范围为±6° 。
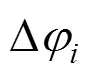

式中=1,2,3,…,为感应同步器一个周期内的误差测试点个数;为谐波次数;Dy表示谐波测角误差幅值;Dφ表示对应初相角。
对式(1)进行转换,可得


式中A与B均为常数;Δ0、Δy与△y为模型参数。
非线性误差转化成线性化后,利用最小二乘法进行线性误差补偿,其拟合速度快、精度高。
在实际工程中,谐波误差的计算过程涉及到浮点运算,在航天应用中,浮点运算多采用DSP予以实现[16-17]。高轨单粒子效应会严重影响DSP的可靠性,在高轨运行系统中,选用FPGA进行系统设计实施。由于宇航级FPGA资源有限,一般能达到百万门,FPGA的浮点运算需要转换成整数等过程,会造成资源的紧张。采用谐波补偿法实现该系统测角误差补偿较为困难。由此,考虑采用分段补偿法,在小范围内对测角误差线性拟合,近似表征真实误差分布。分段补偿方法的原理简单明了,物理意义强,采用FPGA易于实现,符合高轨道应用需求。
2.1 分段补偿原理
扫描测角系统包括扫描测角机构、感应同步器解调电路。因此,扫描测角系统的测角误差包括机构误差和电气误差两部分。由于两部分的误差分离比较困难,误差的精确模型建模也较为困难,因此,采用分段补偿的方法完成扫描测角系统的标定。
分段补偿的前提是:假设误差曲线在小范围内为呈线性变化,对测试系统的要求包括:1)根据以往的工程实践经验,扫描测角系统能够至少以0.25°等间隔微调并测量角度值;2)角度值精确到0.1。
采用的基准装置——经纬仪精度为0.5",对比扫描测角系统的角度位置与经纬仪角度读数,两者之差即为角度误差。每个测试角度位置测试三次取均值作为该点的测角误差。
假设:θ为第个测试角位置,三次测得的角度误差分别为Δθ1、Δθ2和Δθ3,则
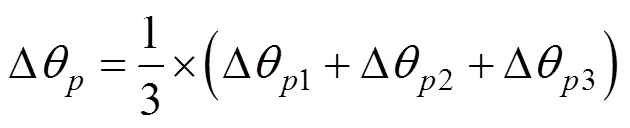
因此,以0.25°为间隔,以Δ(p+1)–Δθ为截距,求得该误差线性段的斜率b。将各段的起始位置点、斜率作为已知项,对采集的角度数据进行补偿,实现分段误差标定。
2.2 分段补偿法的空间适用性
谐波补偿法和分段补偿法都具有理论依据,且具有可实现性。
从测试操作复杂度考虑,谐波补偿法要求每次测试的角位置偏差小于±5,而分段补偿法要求测试过程中每次测试的角位置偏差小于±0.5,才能保证最终插值补偿的精确性。因此,谐波补偿法对测试角度的微调要求较低,易于测试操作。
从高轨道空间环境适应性考虑,谐波误差补偿法需要通过高阶模型的运算来实现测角位置补偿,计算量较大,对芯片计算能力要求高,极大限制了高轨道适应性元器件的选择范围;而分段补偿法恰好弥补了这一不足,只要综合考虑芯片存储量和测角精度要求,选择合适的标定范围实时补偿角位置,实现扫描系统高精度测角。
高轨道空间环境(如单粒子效应等)复杂,选择抗辐照等级高的FPGA作为测角误差标定元件,采用分段补偿方法进行扫描系统测角误差标定。
3 分段补偿法测角精度测试
分别采用谐波补偿和分段补偿两种方法进行同一角位置补偿,得到分段补偿法与谐波补偿法能够达到的精度水平,以评估分段补偿法在应用过程中的精度是否满足需求。为了表征测试数据的有效性,设定经纬仪采集到的扫描镜零位漂移阈值为0.5。具体测试过程如下:
1)利用扫描测试系统,每隔0.5°测试一个角度位置,计算感应同步器和经纬仪的测角误差;
2)将测角误差作为数据源,分别采用谐波误差建模补偿和分段标定补偿获得补偿模型和数据表;
3)将误差补偿模型和误差补偿数据表分别嵌入扫描系统的测定标定模块;
4)将标定后感应同步器读取的数据与经纬仪数据进行对比,即得到系统测角精度。
图2和图3分别描述了谐波误差补偿前后和分段误差补偿前后扫描系统的测角精度。
由图2可知,一个测回中,零位漂移为|0.8–1.1|=0.3,小于阈值要求0.5,因此,该组数据有效。将一个测回内同一测试角位置对应的两个数据取均值作为测角误差,对测角电路进行标定。经过谐波误差标定后,扫描系统的测角误差为±1.8,小于系统要求±2,满足扫描系统的指标要求。
由图3可知,在一个测回中,零位漂移为|3.9–3.5|=0.4,小于阈值要求0.5,因此,该组数据有效。误差处理过程与谐波误差标定过程相同。经过分段误差标定后,扫描系统的测角误差为±1.5,小于系统要求±2,满足扫描系统对指标要求。
综上所述,同一系统采用分段补偿法后测角误差小于谐波补偿法,因此,可以得出结论:对于有限范围的扫描系统,其测角误差分段补偿后所达到的精度能够达到或优于谐波误差法标定后的结果。因此,在高轨道空间相机扫描系统中,采用分段补偿法进行系统误差补偿。
4 结束语
针对空间相机挠性支撑扫描装置的测角精度标定问题,采用经纬仪作为测量手段,配合光电自准直仪监控扫描镜的位置零漂。利用测得的误差对角度解算电路进行分段补偿,并检测扫描系统的测角精度,其精度优于4",满足扫描系统高测角精度的需求。
在后续的工作中,高精度空间遥感相机扫描系统的深入研究还需进一步提高测量系统的现场可实施性、测量方案的可操作性、测量技术的有效性,以及测试设备的大幅度改进等。此外,动态测试也是必然的发展方向,因为,扫描系统是一个运动的系统,考察其动态测角精度更具实际意义。目前,对动态误差的研究已经逐步开展,基于系统静态误差模型分析,引起动态误差的原因[18-19]、多普勒效应[20]等已经引入到建模过程中,在实际误差修正中得到应用。针对测角电路设计的动态补偿方法也已经在试验中表现出有效性[21]。因此,在后续工作中,对空间遥感相机扫描装置的动态特性进行深入分析,进而标定系统的动态测角精度,以指导实际的工作需求。
[1] 陈世平. 空间相机设计与试验[M]. 北京: 中国宇航出版社, 2003.CHEN Shiping. Space Camera Design and Experiment [M]. Beijing: China Aerospace Press, 2003.(in Chinese)
[2] 王恺, 刘兆军. 摆动扫描的迭代学习控制系统研究[J]. 航天返回与遥感, 2008, 29(1): 34-38. WANG Kai, LIU Zhaojun. Iterative Learning Control System of Scan for Oscillating Mirror [J]. Spacecraft Recovery & Remote Sensing, 2008, 29(1): 34-38. (in Chinese)
[3] 任顺清, 曾庆双, 陈希军. 圆感应同步器测角误差的分离技术[J]. 中国电机工程学报, 2001, 21(4): 92-95. REN Shunqing, ZENG Qingshuang, CHEN Xijun. The Angle Measuring Error Separation Technology of Round Inductosyn[J]. Proceedings of the CSEE, 2001, 21(4): 92-95. (in Chinese)
[4] 李婧, 康建兵, 刘雪峰. 感应同步器读数粗精融合与误差修正[J]. 光学精密工程, 2015, 23(10): 381-387. LI Jing, KANG Jianbing, LIU Xuefeng. Data Amalgamation of Coarse and Fine Channels and Error Correction of Inductosyn[J]. Optics and Precision Engineering, 2015, 23(10): 381-387. (in Chinese)
[5] 李秋明, 冯汝鹏, 王景贺, 等. 感应同步器测角系统误差分析及补偿[J]. 中国惯性技术学报, 1998, 6(1): 50-53. LI Qiuming, FENG Rupeng, WANG Jinghe, et al. Error Analysis and Compensation for Inductosyn Angle Measuring System[J]. Chinese Society of Inertial Technology, 1998, 6(1): 50-53. (in Chinese)
[6] 刘承军, 齐明, 邹继斌. 感应同步器测角系统误差建模[J]. 哈尔滨工业大学学报, 2009, 41(9): 51-55. LIU Chengjun, QI Ming, ZOU Jibin. Error Modeling of Inductosyn Angle Measuring System [J]. Journal of Harbin Institute of Technology, 2009, 41(9): 51-55. (in Chinese)
[7] 齐明, 邹继斌, 胡建辉. 神经网络在感应同步器零位误差补偿中的应用[J]. 中国电机工程学报, 2008, 28(9): 105-110. QI Ming, ZOU Jibin, HU Jianhui. Application of Neural Network in Pitch Error Compensation of Inductosyn[J]. Proceedings of the CSEE, 2008, 28(9): 105-110. (in Chinese)
[8] 张翠芳. 基于神经网络的感应同步器测角系统的误差补偿[D]. 哈尔滨: 哈尔滨工业大学, 2008. ZHANG Cuifang. Error Compensation of Angular Measuring System of Inductosyn Based on Neural Network[D]. Harbin: Harbin Institute of Technology, 2008. (in Chinese)
[9] 尚超, 王淦泉, 陈桂林. 基于经纬仪的感应同步器测角精度检测方法研究[J]. 传感技术学报, 2008, 21(5): 865-868. SHANG Chao, WANG Ganquan, CHEN Guilin. Test Method of the Absolute Angle Measuring System with Inductosyn Based on Theodolite[J]. Chinese Journal of Sensors and Actuaors, 2008, 21(5): 865-868. (in Chinese)
[10] 任顺清, 伊国兴, 曾庆双, 等. 小范围回转轴系感应同步器测角系统的误差分离技术[J]. 电机与控制学报, 2005, 9(2): 183-186. REN Shunqing, YI Guoxing, ZENG Qingshuang, et al. Error Separating Technology of Inductosyn Angle-measuring System in Limiting Rotation Axis System[J]. Electric Machines and Control, 2005, 9(2): 183-186. (in Chinese)
[11] 汪逸群, 颜昌翔, 贾平. 非接触式扫描反射镜定位精度检测方法[J]. 红外与激光工程, 2012, 41(4): 1057-1061. WANG Yiqun, YAN Changxiang, JIA Ping. Non-contact Position Precision Detecting Method of Scanning Mirror[J]. Infrared and Laser Engineering, 2012, 41(4): 1057-1061. (in Chinese)
[12] 陈希军, 任顺清. 感应同步器测角误差的自动化检测与补偿[J]. 电机与控制学报, 2010, 14(4): 41-45. CHEN Xijun, REN Shunqing. Automatic Measurement and Compensation of Inductosyn Angular Displacement Error[J]. Electric Machines and Control, 2010, 14(4): 41-45. (in Chinese)
[13] 齐凤梅, 石治国. 圆感应同步器安装误差修正方法研究[J].光学技术, 2006, 32(z1): 445-448. QI Fengmei, SHI Zhiguo. The Installation Error Revise Method Research of Round Inductosyn[J]. Optical Technique, 2006, 32(z1): 445-448. (in Chinese)
[14] 孙泽林, 王昭, 翟唤春. 双经纬仪交会测量火炮调炮精度的误差分析与抑制[J]. 光学精密工程, 2011, 19(10): 2434-2441. SUN Zelin, WANG Zhao, ZHAI Huanchun. Analysis and Control of Error on Two Theodolite Intersection Measurement for Gun Rotated Accuracy of Artillery[J]. Optics and Precision Engineering, 2011, 19(10): 2434-2441. (in Chinese)
[15] 娄莉娜, 朱革, 王先全, 等. 感应同步器测角系统短周期误差的研究及软件补偿[J]. 计算机测量与控制, 2010, 18(8): 1730-1735. LOU Lina, ZHU Ge, WANG Xianquan, et al. Error Research and Software Compensation of Inducotsyn Angle Measuring System[J]. Computer Measurement and Control, 2010, 18(8): 1730-1735. (in Chinese)
[16] 王先全, 吴敏, 冯济琴, 等. 基于FPGA的感应同步器的数据采集和处理的研究[J]. 仪表技术与传感器, 2010, 5(1): 41-43. WANG Xianquan, WU Min, FENG Jiqin, et al. Data Acquisition and Processing for Inductosyn Based on FPGA[J]. Instrument Technique and Sensor, 2010, 5(1): 41-43. (in Chinese)
[17] 沈胜兵. 基于DSP的感应同步器测角系统设计与实现[D]. 哈尔滨: 哈尔滨工业大学, 2014. SHEN Shengbing. Design and Implementation of Inductosyn Transducer Angle Measurement Based on DSP [D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese)
[18] 邓辉宇, 苏宝库. 鉴幅型测角系统动态误差建模研究[J]. 哈尔滨工业大学学报, 2001, 33(5): 646-650. DENG Huiyu, SU Baoku. Dynamic Error Model of Angular Measuring System of Amplitude Discrimination Mode[J]. Journal of Harbin Institute of Technology, 2001, 33(5): 646-650. (in Chinese)
[19] 袁辉, 刘朝晖, 李治国, 等. 圆感应同步器系统误差的动态提取与补偿[J]. 光学精密工程, 2015, 23(3): 794-802. YUAN Hui, LIU Zhaohui, LI Zhiguo, et al. Dynamic Extracting and Compensation of System Error for Rotary Inductosyn[J]. Optics and Precision Engineering, 2015, 23(3): 794-802. (in Chinese)
[20] 张育, 王建字, 刘银年, 等. 感应同步器动态误差分析及修正[J]. 科学技术与工程, 2010, 10(17): 4205-4209. ZHANG Yu, WANG Jianzi, LIU Yinnian, et al. Analysis and Correction of Dynamic Error in Inducosyn[J]. Science Technology and Engineering, 2010, 10(17): 4205-4209. (in Chinese)
[21] 刘强, 尔联洁, 陈敬泉, 等. 基于线性外推原理的圆感应同步器输出动态补偿[J]. 仪器仪表学报, 2004, 25(1): 106-108.LIU Qiang, ER Lianjie, CHEN Jingquan, et al. Dynamic Compensation of Inductosyn Output Based on Linear Extrapolation Scheme[J]. Chinese Journal of Scientific Instrument, 2004, 25(1): 106-108.(in Chinese)
Angle Measurement Accuracy Calibration Method for Space Remote Sensor Scanning Equipment Supported with Flexible Pivots
CHI Dongnan XU Lina ZHAO Xin ZHANG Xiuqian JIA Huili
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
To calibrate the angle measurement accuracy for space camera scanning system supported with flexible pivots,the segmented error compensation method applicable to complex space environment was studied using the angle error data collected from theodolite. Using the photoelectric autocollimator, the zero-angle position of the scanning mirror was monitored, and the measurement shifts with time and environment were determined. According to requirements in high orbit application,it is necessary to use the segmented error compensation method. Taking the angular errors as the input of the compensation system, the angle measurement circuit was calibrated using segmented error compensation method. Then, comparing the test results with those obtained by harmonic error compensation methods, one can find that the angle measurement accuracy after segmented error compensation can satisfy the system performance requirement. Therefore,the validity of the segmented error compensation method is confirmed to achieve high accuracy angle measurement for space camera in limited-angle scanning.
scanning equipment; angle accuracy measurement; calibration method; space camera
TP731
A
1009-8518(2018)05-0089-07
10.3969/j.issn.1009-8518.2018.05.012
迟冬南,女,1985年生,2013年获哈尔滨工程大学控制理论与控制工程专业博士学位,高级工程师。研究领域为空间运动机构控制。E-mail: chidongnan@163.com。
2017-12-28
(编辑:王丽霞)
