上覆高速桥梁对下穿顶管施工的力学响应

熊正元，杨春山

（广州市市政工程设计研究总院，广东 广州 510000）

0 引言

顶管作为一种非开挖技术，越来越多地应用于各种地下管线[1]。顶管推进过程会使周围土层受到挤压、剪切及卸载作用，由此引起地层扰动变形是不可避免的，从而迫使邻近构筑物受到扰动。随着顶管建设的日益增多，顶管施工环境力学效应值得探索。

以顶管下穿高速桥梁实例为依托，分析顶管推进过程力学扰动的内在机理，建立顶管施工过程精细的三维计算模型，探索上覆既有高速桥梁结构对于下穿顶管开挖的力学响应特征，以评价顶管方案的可行性。

图1 顶管与既有桥梁的位置关系

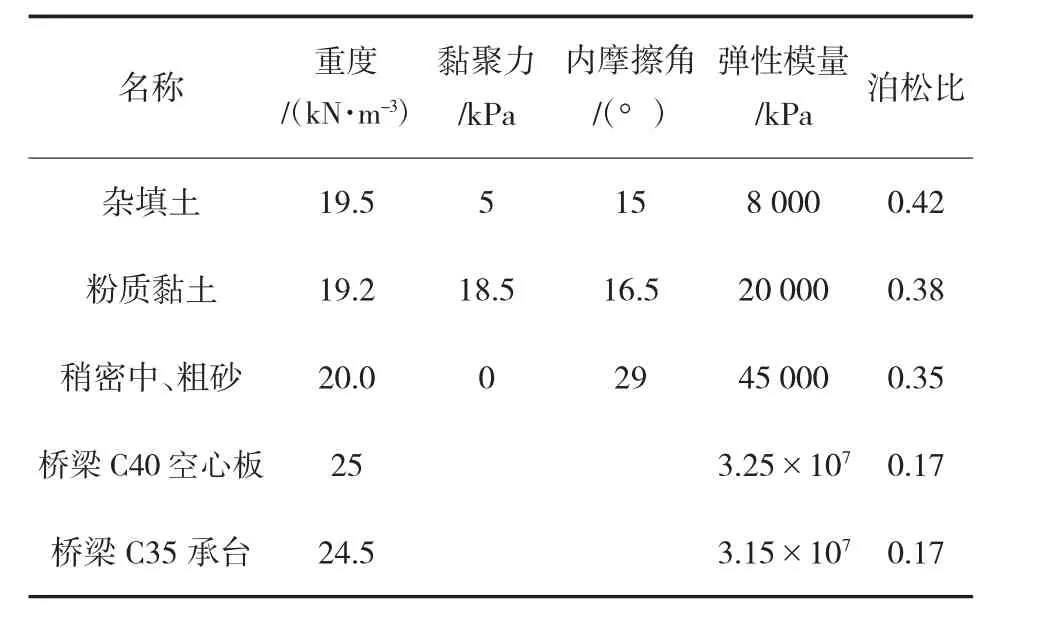
表1 土层-结构物理力学参数

1 工程概况

广州市猎德污水处理系统管网工程中车陂路主涌与长兴路支涌采用顶管法施工，全长约为4.54 km。项目部分顶管区域下穿华南快速路，顶管与既有桥梁结构的位置关系如图1所示。该区段顶管最小埋深约为5 m，管径为800 mm的焊接Q235钢管。根据现场勘察资料与桥梁结构设计资料，可得到表1的土层-结构物理力学参数。

2 顶管推进扰动机理

如图2所示，顶管推进受正面顶进力、地层损失及摩擦力等因素影响，产生应力扰动。顶管施工扰动主要经历三个阶段：

（1）初始应力平衡阶段。在顶管开挖扰动前，土层在自重作用下处于应力平衡状态。

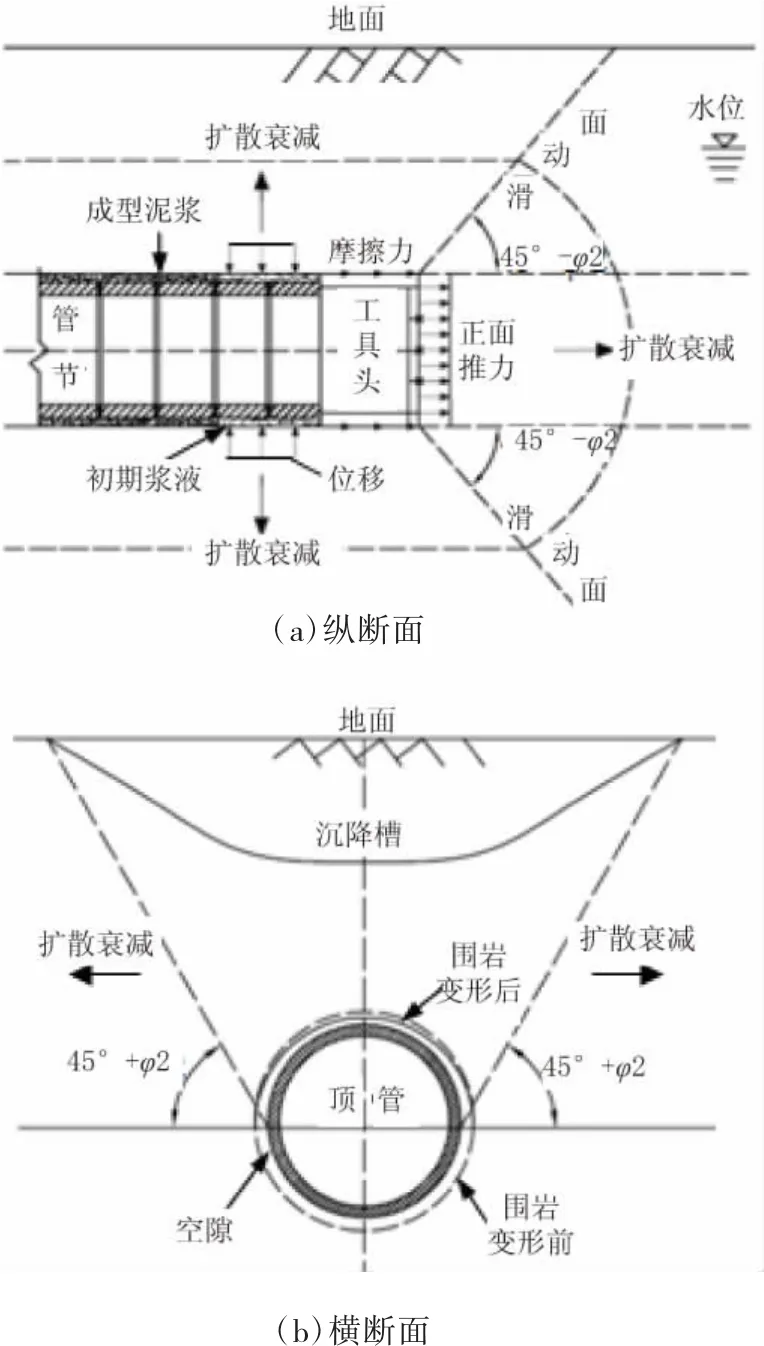
图2 顶管施工土体扰动效应

（2）开挖应力扰动阶段。顶管接近与通过时，土层经历挤压隆起、损失松动，出现明显的变形，并向周围扩散衰减。

（3）注浆变形稳定阶段。随着泥浆的不断注入和硬化，阻止了土层塌陷与松动的发展，扰动后变形逐渐趋于稳定。

顶管前方土体在顶进力作用下处于被动状态，扰动面倾角为45°-φ/2，而管节环向外围土层因空隙的存在表现为主动状态，所以扰动面倾角为 45°+φ/2。

3 桥梁结构对顶管下穿力学响应

3.1 计算模型及工况

模型计算区域选取时，充分考虑了边界效应，X、Y、Z方向计算尺寸分别取54 m、17 m及18 m。整体计算模型、顶管与桥梁结构模型如图3所示。

计算模型中土层、顶管泥浆套、承台、桥台、空心板采用三维实体单元模拟，顶管管道用壳单元模拟。模型中土层用Mohr-Coulomb弹塑性本构模型，既有桥梁与新建顶管则用弹性本构模型。模型中地下桥梁结构与顶管泥浆套通过修改单元属性实现。模型侧向加水平位移约束，底部加竖向约束，顶面为自由面，不加约束。

图3 顶管施工三维计算模型

顶管外环形空隙借鉴盾构注浆等代层[2]的思路，在顶管外围空隙处设置一定厚度的实体单元，等代层厚度近似等于Lee与Rowe[3]提出地层空隙参数G，若不考虑泥浆套，G就是因超挖引起土体向管节的收敛位移，通过下式计算：

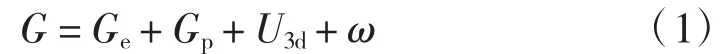
式中：Ge为刀盘切削形成的管道外壁空隙；Gp为顶管机外径与管道结构外径之差；U3d为开挖面形成的超挖土量；ω为顶进施工引起的偏斜或顶进路线为曲线时形成的空隙。

基于实例工况，参考文献[4]的取值方法，该例地层空隙参数G取10 mm，泥浆套等代层实体单元压缩模量Es取5 MPa。顶管开挖正面推进力取开挖面中点的静止土压力±20 kPa[5]，该例推进力约为90 kPa，土体与顶管间截面摩阻力取3 kPa。

模型计算含顶管隧道长度54 m，每次向前推进的长度为1.5 m，分38步顶进完成。此次分析共计40个工况，具体见表2。

表2 计算工况

3.2 地层沉降与模型可靠性分析

图4为顶管通过监控点2D（管径）后的沉降云图，定义位移指向坐标正轴为正，反之为负。图4显示，受顶管开挖造成的挤压、剪切及卸载等作用，周围土层经历应力扰动、重塑及位移等过程，模型表现为整体沉降，最大竖向位移为-2.6 mm，出现在管道顶部，地表最大沉降约为-1.385 mm。

图4 顶管开挖完地表沉降云图

为了考察计算模型的合理性，提取监控点位横向地表沉降，与Peck[6]地表横向沉降槽理论计算结果对比。Peck沉降槽经验公式为

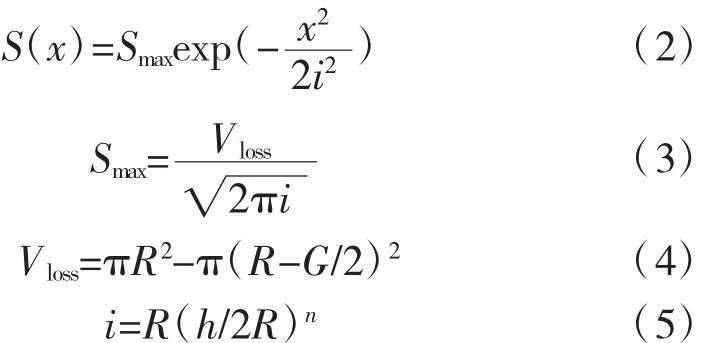
式中：S（x）为x位置地面沉降量，m；x为横向水平距离，m；Smax为隧道轴线上方的最大地面沉降量，m；Vloss为隧道单位长度的土体损失量，m3/m；i为地面沉降槽宽度系数，m；R为顶管隧道外半径，m；h为隧道轴线至地面的距离，m；n=0.8～1，土越软取值越大。

将实例参数代入上述公式，计算得到i=2.7 m，Vloss=0.012 5 m3/m，Smax=1.845 mm。计算不同位置的地表沉降值，并提取相应数值，结果对比如图5所示。

图5地表沉降对比

图5 表明，顶管施工引起的地表沉降分布满足一般的认识，与Peck沉降槽理论计算结果呈现出的正态分布规律吻合，数值计算沉降结果反映了实际地表沉降趋势。然而数值计算位移值较理论分析结果明显更小，最大相差约25%，究其原因是数值计算结果提取的是顶管至监控点后方2D时的沉降值，并非最终沉降值，该值约为总沉降量的75%，与文献[7]的认识相近。由上述分析认为，本文所用计算模型具备合理性。

3.3 既有桥梁结构力学响应

考虑到顶管轴向扰动作用显著小于其他两个方向，故此重点考察Y、Z方向的位移结果。图6为顶管施工完邻近桥梁结构位移云图。

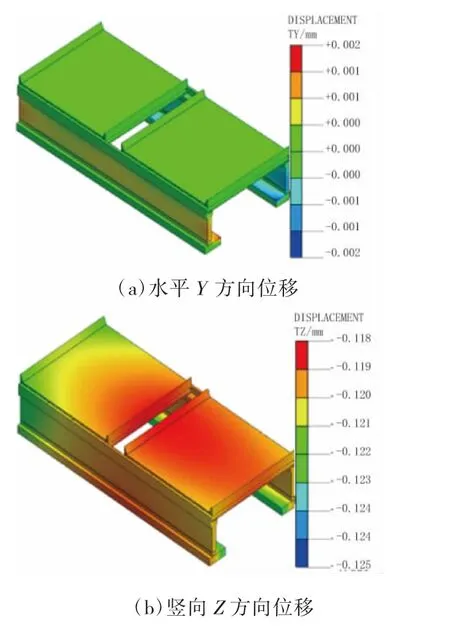
图6 顶管施工完桥梁结构位移云图

图6显示，顶管施工引起的桥梁结构最大位移仅为0.125 mm，远小于控制值5 mm，因此桥梁结构受到影响很细微。由位移结果不难发现，桥梁结构位移总体水平较低，究其原因是顶管管径较小，开挖引起的扰动经土层扩散衰减后，传递至桥梁结构，由此引起桥梁结构力学响应不明显。

图7为既有桥梁结构在顶管开挖前、后的最大主应力云图，定义应力受拉为正，承压为负。从应力云图分布情况来看，顶管施工引起的桥梁结构附加应力很小，然而由于桥梁结构受到长期运营荷载作用，产生的最大主应力为2.114 MPa，超过了结构极限抗拉强度，所以结构处于局部带裂隙工作状态。由桥梁结构位移和应力结果可判断，实例顶管开挖引起的力学扰动较小，桥梁结构处于安全稳定状态，顶管实施方案可行。但考虑到结构带裂隙工作，顶管施工阶段需加强实时监控，以确保顶管施工中桥梁结构的安全问题。

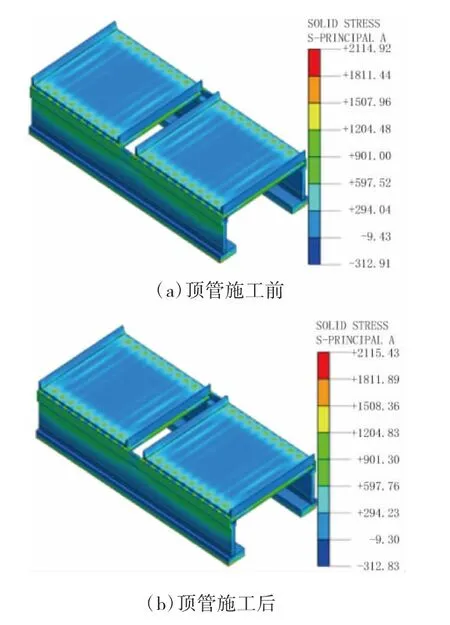
图7 桥梁结构应力云图（单位：kPa）

4 结语

（1）顶管通过监控点2倍的管径后，地表沉降约完成总沉降量的3/4。顶管施工中力学扰动主要经历初始应力平衡、开挖扰动及注浆稳定三个阶段。

（2）顶管施工地表沉降满足Peck沉降槽分布，数值与理论计算规律吻合，所用三维模型具备合理性。

（3）顶管施工引起的桥梁结构附加变形和应力均远小于控制值，顶管设计方案总体可行，但既有桥梁结构处于局部带裂缝状态，需加强施工监控。