再生混凝土钢管柱在低周反复作用下的抗震性能研究

易 轶，杨晓华

（湖南工业大学土木工程学院，湖南 株洲 412007）

有关研究表明：旧建筑拆除产生大量建筑垃圾，其中30% ～50%为废弃混凝土［1］。为解决废弃混凝土处理的污染问题，同时也让其有经济效益，采用废弃混凝土破碎工艺，按照一定级配进行配制，形成再生粗骨料，将再生粗骨料取代天然骨料配制而成的混凝土称为再生混凝土［2］。再生混凝土力学性能与普通混凝土相比，峰值应变增大，强度与弹性模量降低，延性下降，制约了再生骨料混凝土在工程中的应用［3］。将再生骨料混凝土与钢管组合成再生混凝土钢管柱，通过钢管对再生骨料混凝土的约束效应，可有效弥补再生骨料混凝土材料稳定性差的不足；薄壁钢管对局部缺陷很敏感，极限承载力不稳定，核心再生骨料混凝土的存在可有效防止钢管在受到轴向压力时过早发生屈服［4］。

国内外对再生混凝土钢管组合构件的研究主要包括轴压和偏压构件的力学性能及破坏机理，以及再生骨料混凝土钢管柱的耐火性能、承载力和抗震性能［5-7］。其中，关于其抗震性能仍以试验为主，有限元分析较少。

为探讨不同参数对再生混凝土钢管柱抗震性能的影响，本文基于文献［8］，利用有限元软件ANSYS对受约束的再生混凝土钢管柱进行数值模型研究，对不同轴压比、不同再生混凝土强度、不同含钢率等建立有限元分析模型，并与已有试验结果相对比，以验证其正确性。

通过大量模型计算得到不同参数对钢管再生骨料混凝土柱骨架曲线、延性性能、刚度、耗能能力的影响规律。同时，得出钢管再生混凝土柱位移延性系数简化公式，为钢管再生骨料混凝土柱投入实用提供简化计算依据。

1 有限元模拟

1.1 核心区再生混凝土单元类型及本构关系

核心区混凝土采用Solid65单元和William-Warnke五参数破坏准则。轴心抗拉、抗压强度和试验值相同。钢管混凝土核心区的等效约束效应系数为x＝x0，其中钢管面积A0＝混凝土核心区面积A1＝0．25π×d2。

根据以往研究者［9］对普通混凝土的应力-应变滞回关系进行的研究发现，滞回关系的骨架线基本接近于单向加载。因此在模拟钢管再生混凝土柱时，暂以核心再生混凝土单向加载时的应力-应变关系曲线代替其滞回关系骨架线。

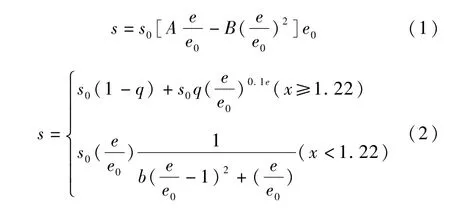
式中，s为再生混凝土压应力；e为相应的压应变；x为约束效应系数；fc混凝土轴心抗压强度标准值；Ec为混凝土的弹性模量；mc为核心区混凝土泊松比。

1.2 钢管及接触对

1）钢管单元类型及本构关系的选取

钢管采用Solid 45单元，钢管的本构（σ-ε）关系包括2个阶段：①弹性阶段（OA段），弹性模量为E；②屈服平台（AB段），屈服强度为fy。

2）接触对所选单元

钢管内表面为目标面，采用三维3节点目标单元Taget170；混凝土外表面为接触面，用三维8节点单元Contact174，这两组单元通过共享常数号与相关接触表面配对。钢管混凝土在轴压比和水平荷载作用下始终保持为平截面。

1.3 有限元模型与参数设置

分离式模型能保证模型具有足够的精度，又能满足模型计算效率，并力求结果准确合理。建立如图1所示的ANSYS有限元模型，钢管单元共计有1 024个单元，混凝土单元共计有2 300个单元，单元尺寸为50mm，柱底采用完全约束。接触分析时，接触的算法为扩展拉格朗日算法［10］。

图1 接触界面模型

2 原试验简介

原试验的研究对象是框架柱，试件设计参数如表1所示。

3 有限元参数分析

取含钢率和轴压比2个因素下的多个不同取值对比，命名规则为zybn-ght，其中zyb代表轴压比，n代表轴压比取值。gh代表钢管厚度，t代表厚度，根据钢管厚度决定含钢率大小。为排除其他干扰因素，选取轴压比为0．2相同强度的再生混凝土，观察含钢率这单一因素下抗震性能的变化。数据参数按照表2取不同工况。

从不同轴压比下的滞回曲线可看出，随着轴压比在0．2～0．5时，承载能力先增加，在轴压比为0．5时幅度值最大，且滞回环面积最大，由此可看出耗能能力最强。由此可知道，在一定程度上，轴压比能够提高再生混凝土钢管柱的延性。由图2可知，当轴压超过0．7时，加快了构件屈服后弹塑性和累积损伤的发展，刚度退化速度加快，承载能力降低，延性降低，曲线下降段的坡度变陡，刚度退化速度加快。主要原因是当轴压比增大时，竖向荷载也增大，P-△效应引起附加弯矩随水平位移的增加在构件内力中的比例增大，因此构件的承载力降低，位移延性减小。再者，轴压比增加，试件弹性阶段的刚度微小增幅，因为在弹性阶段，构件变形很小，P-△效应影响较小。

表1 试件参数

表2 工况

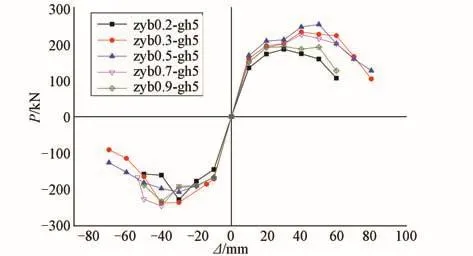
图2 不同轴压比下的骨架曲线

随着含钢率增加，承载能力增大，钢管混凝土柱的延性也提高，钢管再生混凝土柱的耗能能力增加。再生骨料本身塑性的实际性能和假设条件相差较大，有些地方的数据和实际有出入，但整体依然可看出随着含钢率加大，再生钢管混凝土的承载性能和延性也随着增大。

4 试验与有限元对比结果及分析

每一个荷载步的荷载子步会逐次调整荷载子步数和收敛步数试算；构件受力的开裂和破坏的荷载步时，位移加载采用位移的无穷范数控制收敛。

4.1 试验及模拟现象

模拟中钢管底部受压一侧开始出现微小的屈曲外凸现象。正向卸载和反向加载过程交替进行，钢管另一侧也开始出现鼓曲，圆管在底部主应力较大，且有相应的变形，试件破坏时钢管底部已屈服，承载力达到极限，柱根部的破坏状态和试验结果一致。当达到极限承载力时，钢管壁在支座处所承受的应力最大，而核心混凝土所承受的应力很小且试件均为底部屈服。

4.2 滞回曲线

分析试件试验和数值模拟得出的滞回曲线，可发现各模拟与试验总体大致比较吻合。有限元分析滞回环面积较为饱和的原因是因为试验过程中钢筋混凝土材料本身的离散性带来的损伤，从而造成试验值偏小。

1）试验和模拟都可看出再生混凝土钢管柱的滞回曲线形状均呈梭形，曲线斜率不断减小，试件刚度不断退化。二者比较吻合，能够看出再生骨料本构修正模型较合理。

2）由试件ZSGZ2和ZSGZ5-2的滞回曲线可知，构件承载能力及延性随钢管壁厚的增加而提高，试件ZSGZ5-2的钢管厚度增加，耗能能力大，延性性能好；试件ZSGZ2的含钢率低，滞回曲线不如试件ZSGZ5-2饱满；由试件ZSGZ5-1和ZSGZ5-2的滞回曲线对比，无论是试验和模拟均表明，轴压比越大，构件的水平承载力和弹性范围内的刚度也越高，试件ZSGZ5-2在达到峰值荷载后的承载力下降较明显，试件ZSGZ5-1的位移变形大于试件ZSGZ5-2，在一定范围，轴压比越小，其延性和耗能能力越好。

4.3 骨架曲线

各试件的骨架曲线对比如图3所示。在弹性范围内，水平荷载与位移呈线性关系，随着轴压比和钢管厚度的增加，柱的承载能力和刚度也增加，因为在弹性阶段，构件的变形小，P-Δ效应对构件的影响不明显。塑性阶段后期，构件水平承载力继续随轴压比和含钢量的增加而增大，轴压比越大，构件屈服后累积损伤发展也加快，故变形性能降低，构件的水平承载力达到峰值荷载的85%左右，试件破坏时，最终钢管表面鼓曲或底部拉裂。

图3 试件试验与模拟骨架曲线

4.4 刚度退化曲线

试验加载过程中随着位移和加载次数的增多，试件的非线性变形及累积损伤会不断变大，试件的刚度将不断退化。计算刚度退化曲线公式如下：

再生混凝土钢管柱的刚度退化曲线如图4所示。由图4可看出，轴压比越大的构件，曲线下降段越陡，承载力下降快，则刚度退化越快，在弹性阶段内，试件刚度随轴压比的增加而有所提高。含钢率低的试件，刚度退化较快，承载力低。

表3 试件试验／模拟结果

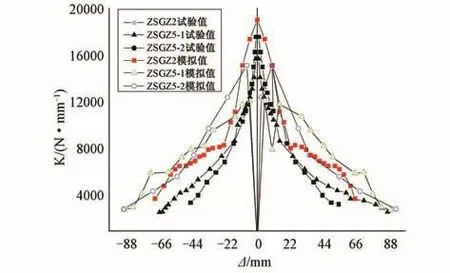
图4 试件试验与模拟刚度退化曲线

4.5 延性和耗能能力

延性系数μ按下式计算：

式中，Δu定义为水平抗力到峰值抗力时的柱顶位移；Δy为屈服位移，定义为最外层钢管初始屈服时对应的柱顶位移，极限位移角按照极限位移与构件长度的比值计算。

由滞回曲线及骨架曲线计算得到各试件的结果试验值和模拟值如表3所示。试验的延性系数在3．55 ～4．76，模拟的延性系数在3．86 ～4．94，误差在8．7%左右，可看出再生混凝土钢管柱具有良好的变形性能。试件延性随含钢率的增加而降低，随轴压比的增加而有所提高。试件ZSGZ2的耗能系数接近0．1。另2个试件的耗能系数在0．12左右，且随着轴压比的增大而减小，试件耗能能力降低。

由表3可知，试验和模拟的耗能系数的相对误差在5．7% ～18．5%，延性系数的相对误差在3% ～8%。由此可进一步验证修正本构模型的合理性，并可将此用于相类似的结构工程实例中。

5 结语

1）应用ANSYS软件建立的模型模拟再生混凝土圆钢管柱的水平位移-荷载曲线和裂缝分布，经比较模拟结果后试验结果后证明了模型的合理性。

2）用有限元分析轴压比和含钢率2个参数作用下的滞回性能，发现试验和模拟结果有较好的吻合性，同时进一步分析多个参数下的骨架曲线和滞回曲线，发现钢管再生混凝土的最佳轴压比在0．5～0．7，随含钢率提高，滞回曲线越加饱满，承载能力和耗能能力也均提高。

3）分析进一步表明，再生混凝土钢管柱的滞回曲线为梭形，再生混凝土钢管柱存在剪切变形，但延性性能和耗能能力良好，能够满足结构设计要求。