求解双层弹性膜单侧接触问题的Uzawa算法*

严月月， 钟艳丽， 郭楠馨

(重庆师范大学 数学科学学院，重庆 401331)

双层弹性膜问题的数值模拟是近年来广受关注的一个问题，问题的数学模型是建立在弹性基本定律上的，遵循以下两个原理：两个膜之间不能相互渗透；在两个弹性膜的接触面，遵循牛顿的作用——反作用定律，即每个膜对另一个膜有相同的作用。由这些理论，便可得到一个由偏微分等式和不等式构成的数学模型，并利用变分原理可得到相应的变分形式[1-2]。由文献[3]可知该问题的解存在且唯一。给出一种求解上述问题的Uzawa算法，并证明该算法的收敛性。通过数值算例验证该方法的有效性。

1 双层弹性模问题及变分形式

讨论如下弹性膜问题：

(1)

其中Ω⊂R2是一个有界、连通的开集，且边界∂Ω为Lipschitz连续的。

在这个模型中，u1和u2是未知量，表示两个膜垂直方向的位移，Lagrange乘子λ表示第二个膜在第一个膜上的作用量，f1和f2是外部压力。模型中的边界条件意味着第一个膜在距离边界∂Ω为g时固定(g是一个非负函数)，第二个膜在边界处固定。

首先引入几个函数空间：

凸子集：

Λ={χ∈L2(Ω);χ≥0几乎处处在Ω上}；

凸集：

为了考虑边界条件g的非负性，锥定义为：

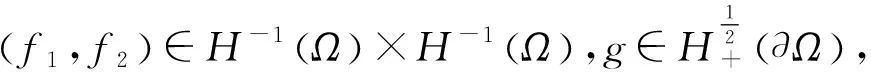
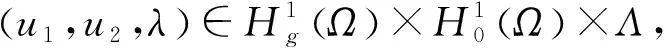
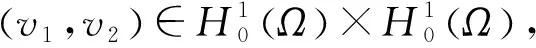
由文献[4]知道问题(2)满足如下结论：

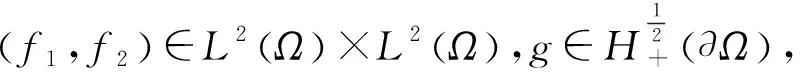
‖u1‖H1(Ω)+‖u2‖H1(Ω)+‖λ‖L2(Ω)≤

a(w，z)≤μ|w|H1|z|H1

(4)

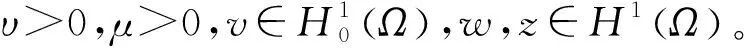
若a(v，v+)≤0，则v+=0(其中v+=max(0，v))。

(5)

那么对于等式

(6)

左右两边同时乘以v1和v2，利用Green公式可得到如下变分等式：

由文献[7-8]可知u1-u2≥0，λ≥0，(u1-u2)λ=0等价于λ=max(0，λ+c(u2-u1))，其中c>0，λ≥0。因此得到问题(1.1)的等价变分投影形式如下：

(8)

2 Uzawa算法及收敛性分析

利用式(8)和文献[9]中的Uzawa算法，从而得到求解问题(1)的Uzawa算法，具体过程如下：

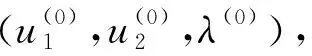
置k=0，γ为足够小的正参数；

第二步由

解出λ(k+1)；

第三步求解问题

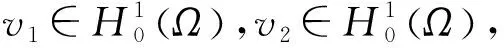
第四步停止或返回第二步。

利用以上算法原理和问题的性质，可得如下收敛性定理：

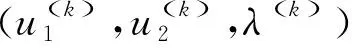
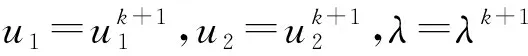
(9)

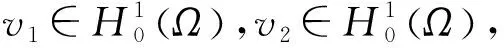
(10)

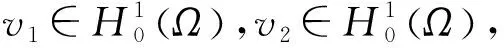
由式(9)减去式(10)可得：

(11)

在式(11)中令

再把两式相加可得：

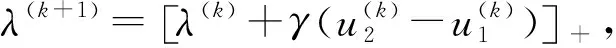
因此

‖λ(k+1)-λ(*)‖2=

所以有

‖λ(k+1)-λ*‖2，

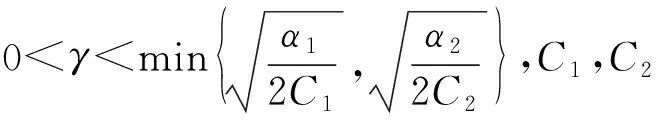
所以有

3 数值算例

用本文方法对问题(1.1)进行数值测试。考虑在正方形区域Ω=(-1，1)×(-1，1)上的极坐标(r，θ)，令g=0.05，0≤θ≤2π，(u1，u2，λ)是问题式(1)的解，其中

u1(r，θ)=g(2r2-1)，0≤r≤1

相应的，满足(1)的f1，f2如下：

膜的位移u1-u2数值解结果如下图所示：

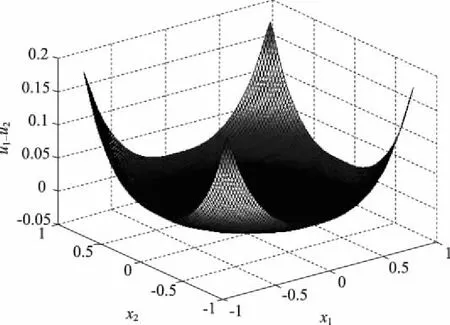
图1 u1-u2数值解结果Fig.1 Numerical results of u1-u2

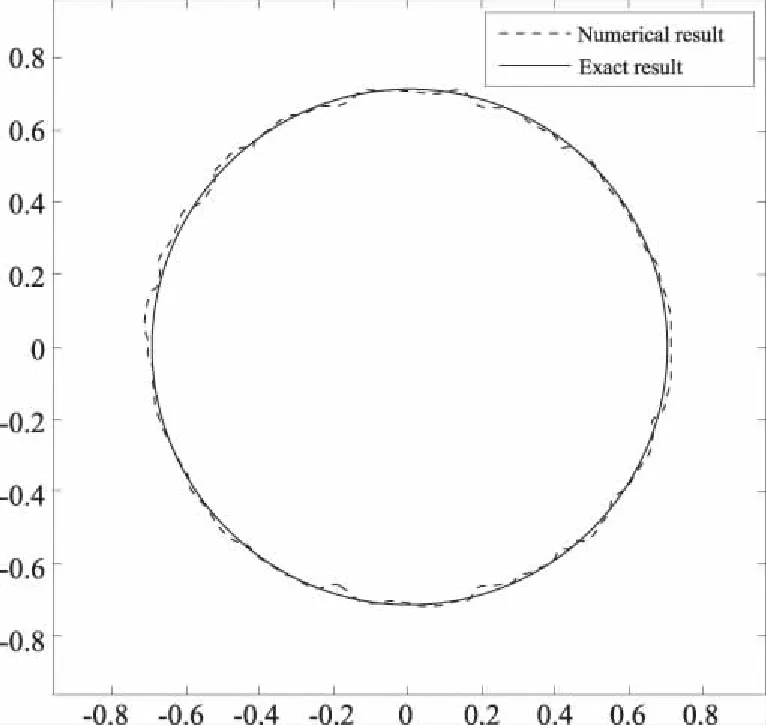
图2 自由边界的数值解和解析解结果Fig.2 Numerical solutions and analytical solutions of free boundary