基于粒子滤波的混沌同步性能研究

任凤娟，冯四风

（1. 郑州城市职业学院，河南郑州，452370；2.上海普华诚信信息技术有限公司，上海，454003）

0 引言

在混沌通信中，通信系统收发双方的混沌同步是一个关键技术。随着人们对混沌同步以及混沌通信的深入研究，基于状态空间的自适应滤波同步方法应运而生。扩展卡尔曼滤波(EKF)和无损卡尔曼滤波(UKF)在对于个别特殊的环境有较好的滤波效果，但缺乏对普遍的非线性、非高斯问题的处理能力。在低信噪比情况下，这两种混沌同步方法的性能不是很理想。粒子滤波算法适合用于处理各种非线性、非高斯问题，更适于混沌通信过程中的信号处理问题。本文研究了粒子滤波算法，对混沌同步问题进行了数学建模，实现了基于粒子滤波的混沌同步。仿真表明，同EKF和UKF混沌同步相比，粒子滤波混沌同步的鲁棒性更好，在相同信噪比下，其同步误差相对更低。

1 混沌同步

在混沌保密通信中，相干解调的保密性能更好。然而，相干解调需要系统发送端和接收端的混沌信号的同步，通过同步信号解调出信息数据。因此，混沌同步就成为混沌保密通信中的关键技术之一。

1.1 混沌同步模型的建立

考虑到一维离散混沌信号，混沌通信过程中的混沌同步问题可以被描述为一般的状态空间模型：

（1）式为状态方程，（2）式为量测方程。其中 xn∈ℜn，表示状态变量，yn∈ℜm，表示观测变量（ n,m均为正整数）；f(xn-1)表示非线性状态转移函数；C = 1 为观测向量；vn和wn表示相互独立的过程激励噪声和观测噪声，假设 vn在任何时刻都为零，wn～(0,σw2) 为正态分布的高斯白噪声。

考虑到Tent混沌系统，Tent的映射公式表示为xn+1= a - 1 - a xn, (1 ＜ a ≤ 2 )，当参数a选择合适时，其值可均匀的分布在[-1,1]这个范围之内，则（1）式中的非线性状态转移函数可以替代为Tent混沌映射。

1.2 滤波器的混沌同步

滤波器的混沌同步就是利用带噪声的观测值ny估计系统状态的真值nx，即混沌系统状态的最优估计问题，基于滤波器的混沌同步原理框图如图1所示。

图1 滤波混沌同步原理框图

用于混沌同步的滤波算法有EKF、UKF和粒子滤波等，其中EKF是经典卡曼滤波方法的一种推广，它以一阶线性化思想为基础，把后验分布近似为高斯分布，将状态方程和观测方程线性化了。UKF以确定的一组采样点经过真实的非线性函数变换后对需要近似的后验分布的均值和方差可以精确到三阶泰勒展开式，且在滤波过程中不需要计算雅克比矩阵。然而，EKF和UKF都只适用于高斯分布的状态，当系统状态呈现出多峰值时，这些方法的滤波性能就会恶化。粒子滤波算法基于蒙特卡罗的思想，它通过大量的粒子来近似系统状态的后验概率分布，弥补了EKF和UKF的缺点。

2 滤波算法

2.1 EKF算法

EKF是经典卡尔曼滤波器的改进形式，同经典卡尔曼滤波原理基本一致。EKF算法主要分为预测和更新两个部分。在状态空间模型（1）和（2）基础上，其具体算法如下。

（1）时间更新（预测）状态一步预测：

由此可见，EKF通过在最优估计点附近计算非线性函数的泰勒级数并将高阶分量舍弃，进而将非线性系统近似线性化以达到可以处理非线性问题的目的。

2.2 UKF算法

UKF结合了无损变换和卡尔曼滤波算法，应用于非线性高斯系统的状态估计中。在状态空间模型（1）和（2）基础上，该算法具体步骤如下：

先对系统状态进行初始化：

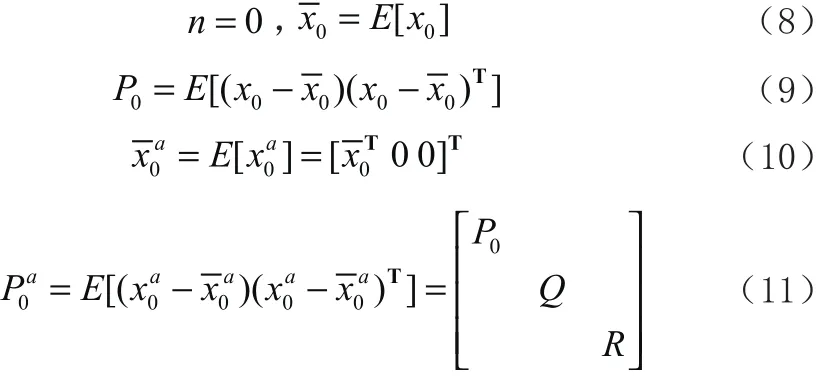
式中的Q和R为过程噪声和测量噪声的协方差矩阵。

（1）用无损变换求系统状态的一步预测xˆn|n-1，求误差协方差一步预测 Pn|n-1

（2）用无损变换求σ通过测量方程的传播点

2.3 粒子滤波算法

粒子滤波的思想基于蒙特卡洛方法，它是利用粒子集来表示概率，可以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布，是一种顺序重要性采样法。由于粒子滤波算法中没有将非线性系统线性化，所以在处理非线性问题时随机变量不必满足高斯分布，能够适用于各种非线性、非高斯模型。

在状态空间模型的基础上，粒子滤波具体算法如下：

（2）重要性采样：采用状态方程作为重要性采样函数。

（3）利用带噪声的观测信号 yn计算重要性权值：

3 仿真结果

Matlab仿真中设置粒子滤波算法的粒子数为5000，混沌信号由Tent混沌系统产生。粒子滤波算法在经过重采样之后很快就会出现了粒子匮乏现象。因此，需要对粒子加入扰动，以增加粒子的多样性，提高粒子滤波的整体滤波性能。如图2所示为信噪比为10dB时一段长度为50的混沌序列的混沌同步。从图中可以看到，粒子滤波同步方法可以较好地同步系统的混沌信号，并且同步性能稳定。

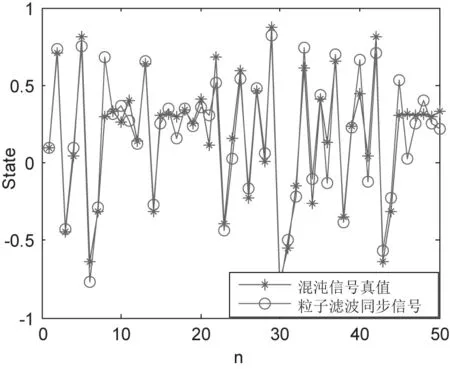
图2 粒子滤波混沌同步

图3 不同信噪比下各同步方法的同步均方误差

定义同步信号和原混沌信号的均方误差为混沌同步的均方误差，不同信噪比下各混沌同步方法的均方误差曲线如图3所示。由图可知，信噪比较高时，各混沌同步方法的均方误差相差不大，且随着信噪比的增大，各同步方法的均方误差逐渐趋近于零。然而，信噪比较低时，EKF和UKF的混沌同步均方误差曲线相近且UKF稍低于EKF，粒子滤波混沌同步的均方误差曲线则明显低于以上两种同步方法，这说明在低信噪比下，粒子滤波混沌同步性能优于EKF和UKF的混沌同步性能。

4 总结

文中研究了粒子滤波算法的混沌同步。首先对混沌同步问题进行数学模型的建立，然后在数学模型的基础之上构建粒子滤波器来估计混沌系统的状态以实现混沌同步。最后比较了EKF、UKF和粒子滤波这三种混沌同步方法在不同信噪比下的混沌同步的均方误差。仿真结果表明，在信噪比较低时，粒子滤波混沌同步具有更低的均方误差，更稳定的同步性能。