基于Simulink的精馏控制仿真研究

田彦彦

(郑州工业应用技术学院，河南郑州，451100)

1 精馏工艺概述

精馏是石油化工等众多生产过程中广泛应用的一种传质过程，主要是使混合物料中的各组分分离，组分分别达到规定的纯度。分离的机理是利用混合物中各组分沸点不同，使液相中的低沸物和汽相中的高沸物互相转移，进而实现混合物料的分离[3]。精馏塔、再沸器、冷凝器、回流泵和回流罐等设备构成了一般的精馏装置，如图1所示。

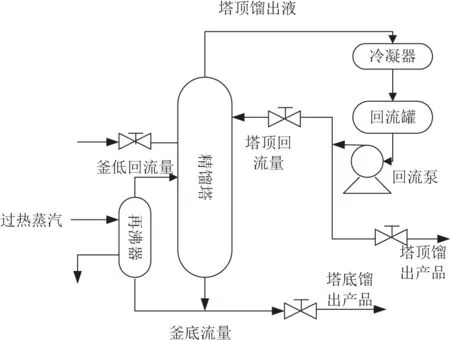
图1 精馏设备与精馏过程

2 控制要求及系统分析

在分离混合物的精馏过程中，精馏塔气相的空间速度的维持主要通过再沸器的加入蒸汽量多少来控制。再沸器一旦加热蒸汽量太大，增大再沸器传热间壁两边的温差，被加热液体一侧产生的气泡容易连成一片，大幅度降低了实际传热效率。

在分离混合物的精馏过程中，调节加热蒸汽量时具有反向响应，具有反向响应特性的对象控制比较困难，而冷凝液储槽的液位变化基本上是与加热蒸汽量成比例关系，所以精馏控制系统中再沸器加热蒸汽量的控制不需要设计非线性调节器，而可以直接运用线性调节器[4]。

由于蒸汽在分离混合物的精馏生产过程中，维持精馏塔气相的空间速度主要通过控制再沸器的加入蒸汽量来实现。蒸汽加入量的变化依次要通过再沸器、精馏塔、冷凝器到储槽，再影响到液位的高低变化，被控对象具有较大的滞后特性，因此控制系统采用PID调节器。冷凝液储槽液位测量时利用压差变送器进行检测。

3 控制系统数学模型

在通常的精馏控制系统中，各参数可根据相应的精馏工艺确定理论值，然后对次要参数进行独立的闭环控制，对产品质量影响较大的主要参数，采取串级、解耦、比值等有针对性的控制方式[5]。本文主要利用Simulink对再沸器加热蒸汽的连续流量与限幅控制进行综合仿真研究。

假设广义控制对象，即从再沸器中蒸汽流量开始，到储液槽液位，系统控制对象的数学模型为：

从再沸器中蒸汽流量至精馏塔内压力变送器的数学模型为：

精馏塔内压力与蒸汽限制流量关系表达式为：Q(s)=Q-0.48P(s)，表达式中P(s)为塔内压力最大值，Q为蒸汽的最大流量，Q(s)为蒸汽的限制流量。

4 系统控制参数整定和分析

建立一个基于Simulink功能模块的精馏控制仿真平台，由广义被控对象的Bode图可知Gm=3.49dB(at 0.0373 rad/sec), Pm=76.5 deg(at 0.02rad/sec)，开环系统在无调节器时稳定，相位稳定裕量值为76.5°，幅值稳定裕量值为3.49dB，对应幅值为1.5。记录此时的震荡周期 Tcr=170s和比例系数 Kcr=1.5。蒸汽压力调节器选择PI调节器，形式为Kp+ Ki/s，与先行微分(1 + KPs)构成微分先行PID。

先让 Ki= 0 ，调整 Kp使系统等幅震荡（由广义被控对象的Bode图知，在 Kp=1.5系统附近震荡），此时系统临界稳定状态。

记录此时的震荡周期 Tcrr=170s和比例系数 Kcr=1.5。

当串联常规 PID的形式为 K’p+K’I/s+K’Ds时，k’p=1.5/1.7=0.9,K’I=K’p/(0.5 Tcr)=0.01,K’D=0.125 TcrK’p=19.1。

常规串联PID形式与微分先行PID形式的关系为:

5 精馏控制系统仿真

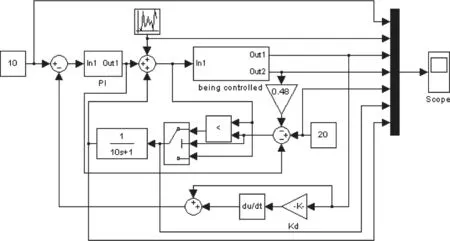
图2 控制系统仿真框图

建立精馏控制系统仿真Simulink框图如图2所示。

将式(4)的整定参数带入图2进行仿真，得到仿真结果如图3所示。由图3所知，系统实现了控制要求。精馏系统具有良好稳定性，稳态时间持续约为300S左右，因此能满足一般精馏过程控制的需要。系统经过低通滤波过程，矩形脉冲波形被原蒸汽流量限制，最终变成了具有变化平坦幅值略低的波形，意即滤除了系统中的高频成分，大幅度降低了带给系统的干扰。

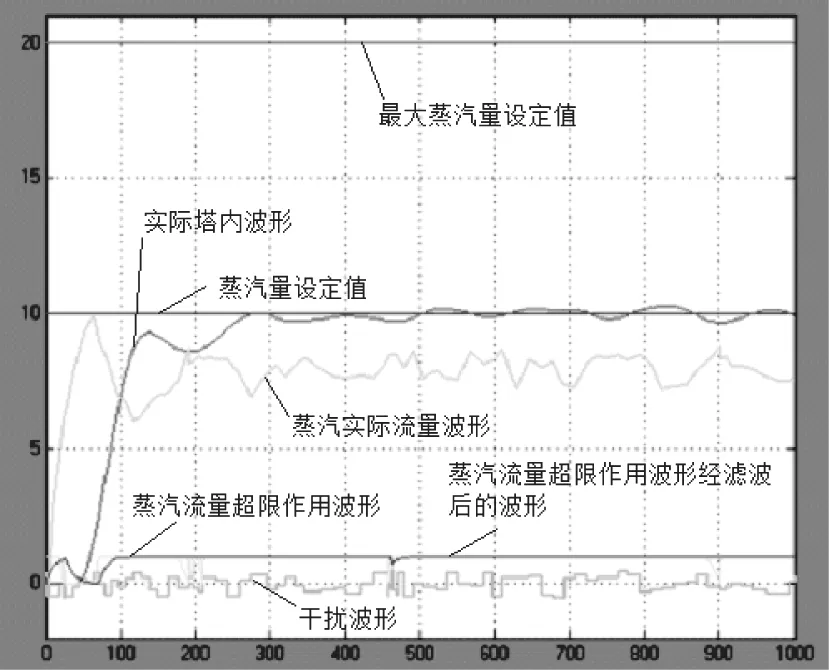
图4 再沸塔控制系统Simulink仿真结果

将式（5）代入图2进行仿真，图4为仿真结果。由图4可知，控制系统实现了控制要求，系统稳态时间持续约为200S左右，具有较好稳定性，能满足一般精馏生产过程控制的需要。经过低通滤波处理后，矩形脉冲波形及锐三角波形被系统中原蒸汽流量限制，最后变成了变化平坦幅值略低的波形，对比图3和图4可知，两组仿真结果系统都实现了控制要求，而且在稳定性、响应速度等方面相差不大。

6 鲁棒性分析

在图2控制系统中仅考虑蒸汽压力控制中延时常数变化±10%时，系统鲁棒性以及其他参数变化分析方法与此类似。随着延时常数变化，系统各个输出波形有明显变化，但各输出幅度没有明显改变，系统的稳定性和精确性变化不明显，说明系统在延时常数变化时仍能正常工作，系统的鲁棒性较强。

7 结语

文章以再沸器加热蒸汽的连续流量与限幅控制为例，在确定控制对象的数学模型后，分析被控对象的稳定性并整定控制参数整定，最后在Simulink进行系统仿真[6]。通过两组仿真的结果，系统都实现了控制要求，而且在稳定性和响应速度等方面相差不大，然后进行鲁棒性分析，由再沸塔控制系统Simulink仿真结果波形可以知道随着延时常数的变化[7]，系统各个输出波形有明显变化，但各输出幅度没有明显改变，系统的稳定性和精确性变化不明显，说明系统在延时常数变化时仍能正常工作，系统的鲁棒性较强。