圆锥曲线中有关弦长问题的探讨

苑 扬

(河北省衡水第一中学 053000)

在解析几何中，学习直线与圆锥曲线的位置关系中，往往会涉及弦长问题，然而这部分又是学生的弱点，如果能熟练地运用弦长公式求解，则必会让解题变得轻松、简洁.下面通过以下几例来说明有关弦长问题的解法，供大家参考.

求直线与圆锥曲线相交的弦AB长的方法是：

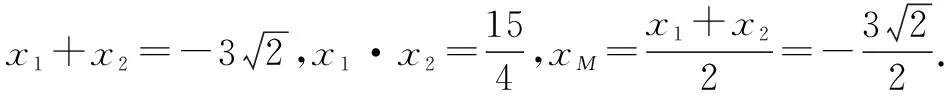
点评也可让学生利用“焦半径”公式计算.

(1)求证：抛物线与直线相交；

(2)求当抛物线的顶点在直线下方时，a的取值范围；

(3)当a在(2)的取值范围时，求抛物线被直线截得的弦长的最小值.

点津抛物线顶点在直线下方的充要条件是：顶点的坐标满足不等式y<2x.

求弦长的最小值，通过设交点(设而不求)确定目标函数f(a)，由a的取值范围可得f(a)的最小值.

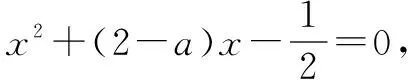
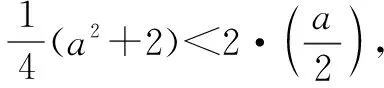
例3 已知抛物线方程为y2=2p(x+1)(p>0)，直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3，求p的值．

解设l与抛物线交于A(x1,y1),B(x2,y2),则|AB|=3.由距离公式

消去x,得y2+2py-p2=0.

Δ=(2p)2+4p2>0，

∴y1+y2=-2p,y1y2=-p2.

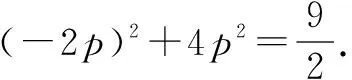
涉及弦长问题，常用“韦达定理法”设而不求计算弦长(即应用弦长公式)；涉及弦长的中点问题，常用“点差法”设而不求，将弦所在直线的斜率、弦的中点坐标联系起来，相互转化.同时还应充分挖掘题目的隐含条件，寻找量与量间的关系灵活转化，往往就能事半功倍.