深水海底管道屈曲扩展非线性有限元分析

佟光军，胡知辉，于 莉，唐 彪

中国石油集团海洋工程有限公司，北京 100028

海底管道包括油气外输管道（export line）、出油管道（flowline） 和注入管道（injection line），是海上油气开发生产系统的重要部分。由于管道初始几何缺陷或外力引起的缺陷，外静水压力可能使管道发生系统压溃（system collapse）。管道压溃一旦发生，会引发扩展屈曲（propagation buckling），直到小于临界水深为止，造成管道系统破坏的严重后果。从费用和备管考虑，对可能发生扩展屈曲的管道间隔设置止屈器（buckle arrestor），阻止管道扩展屈曲穿越（crossover）止屈器。这样管道的扩展屈曲破坏只能发生在两个止屈器之间，不致造成整个管道系统破坏。深水海底管道在安装期和运营期由于承受高静水压力，扩展屈曲问题更应引起关注。

自1975年Palmer首次提出管道扩展屈曲以来，国内外学者开展了大量的理论研究、有限元模拟和实验验证工作。Kyriakides等对于管道系统压溃、屈曲扩展和止屈穿越开展了试验研究，并进行了有限元准静态和动态模拟分析，深入研究了整体式和扣入式止屈器的止屈效率[1-6]。余建星等采用二维环模型进行理论研究，进行了大尺寸管试验研究和有限元准静态及动态模拟分析，对止屈器形式和设计流程进行了总结，并进行了准静态和动态有限元模拟分析[7-11]。龚顺风等对海底管道压溃和屈曲扩展进行了实验研究和有限元准静态模拟分析[12-13]。XUE Jianghong对腐蚀海底管道进行了非线性有限元屈曲扩展模拟分析[14]。

深水油气田开发生产系统的海底管道运行在高设计压力下，由承压（burst）准则和系统压溃准则确定的管道径厚比（D/t）较小，甚至海底管道扩展屈曲校核超出规范公式的适用范围，如DNVGL-ST-F101扩展屈曲校核公式适用于15＜D/t2＜45，在超出规范公式适用范围的情况下，应进行有限元模拟分析。

1 有限元模拟

以某深水油气田出油管道为例进行基于ABAQUS的屈曲扩展的准静态有限元模拟研究。出油管道采用单层管结构，外径D=273.1 mm，壁厚t=19.0 mm，钢管材质API 5L X65 MO SAWL，不考虑腐蚀裕量和壁厚偏差影响，安装水深1 850～2 150 m，海水密度1 037 kg/m3。

1.1 Riks法

Riks法[15]属于双重目标控制方法，即在求解过程中同时控制荷载因子和位移增量的步长。Riks法的迭代求解过程如图1所示。

图1 Riks法迭代求解过程

由图1还可以发现，Riks法的荷载增量步长Δλ是变化的，可以自动控制荷载，但这个过程又使得原来的方程组增多了一个多余的未知变量，因此要想求解还需要补充一个控制方程，即：

式中：nd为荷载步期望收敛迭代的次数，通常取为6；ni-1为前一荷载步的迭代次数，大于10时取10。

当j=1时，根据前一个荷载步i-1收敛结束时的构形，求得用于第i个荷载步收敛计算的切线刚度矩阵[Ki]，即图1中的所示求解半径的线段斜率。由式（2）可得到{Fref}相应的切线位移，即：

需要补充如下关系式：

若在计算中考虑材料塑性的影响，则每个迭代步的切线刚度矩阵需要以当前迭代步的构形为准，即图1中的切线不再平行。

1.2 材料非线性

钢管的应力-应变关系采用Ramberg-Osgood材料应力-应变本构模型。Ramberg-Osgood模型方程形式简单，能较好地模拟管道的弹塑性变形，广泛应用于海底管道材料非线性研究。API-STD-1104给出了相关推荐公式[16]。

式中：ε为应变；σ为应力，ksi（1ksi=6.895MPa）；E为杨氏模量，ksi；σy和Y为最小屈服强度，ksi；T为抗拉强度，ksi；n为应变硬化指数；εt为均匀应变。

ABAQUS模拟分析应采用真实的应力和应变。

式中：σtrue为真实的应力，ksi；εtrue为真实的应变。

1.3 局部缺陷

在管端x=0区域设置局部椭圆度缺陷，使引发静水力压溃，从而产生扩展屈曲。初始局部缺陷由下列公式表示。

式中：w0为径向位移，mm；θ为极角坐标，rad；Δ0为初始局部椭圆度；D为钢管外径，mm；x为沿管轴向坐标，mm；β为缺陷参数；Dmax为局部缺陷最大外径，mm；Dmin为局部缺陷最小直径，mm。

1.4 建模

使用ABAQUS软件建立有限元模型，考虑到管道屈曲扩展问题对称性，建立1/4的管道模型。通过坐标原点的平面x=0、y=0、z=0均为对称面，模拟管道长度取L=20 D，局部缺陷在管端z=0附近，局部缺陷椭圆度最大值Δ0=0.02，β=4.6，几何模型如图2所示。材料非线性本构关系服从各向同性硬化的J2塑性流动准则，采用Ramberg-Osgood模型，API 5L X65的Ramberg-Osgood材料本构关系如图3所示。

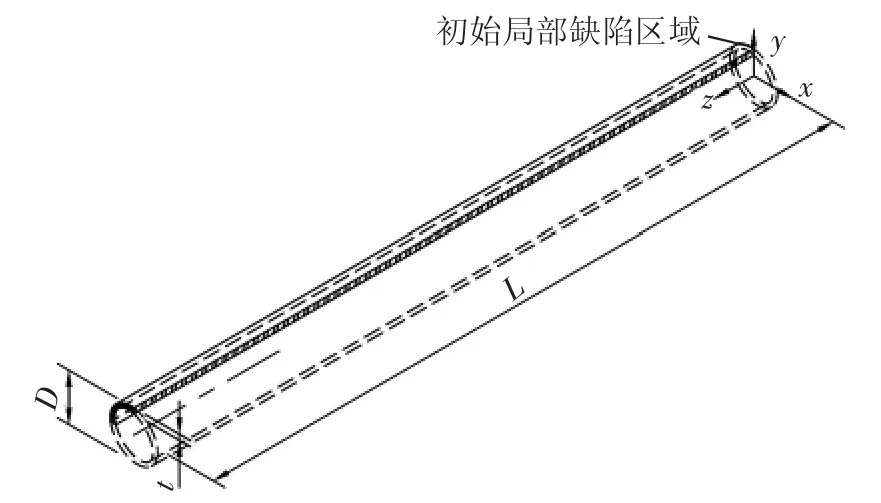
图2 几何有限元模型

图3 API5LX65的Ramberg-Osgood材料本构关系

采用3D六面体单元C3D8I来划分网格，钢管在厚度方向划分为3等份，在圆周方向划分为20等份，在长度方向划分为400等份。施加边界条件，在x=0、y=0和z=0平面内的节点施加对称约束；管端z=L平面内节点平动自由度施加固定约束。

管道压溃后内壁会产生接触，为此在出现接触的对称面y=0上设置解析刚性面。

1.5 分析结果

管子外表面施加静水压力，采用Riks法（Riks法可跟踪加载历史）求解。随着静水压的增加，由于初始几何缺陷（截面局部椭圆化），管子首先在z=0附近产生屈曲压溃，丧失稳定并产生扩展屈曲。求解中的外部压力随弧长变化曲线见图4。局部屈曲压溃和屈曲扩展过程如图5所示。

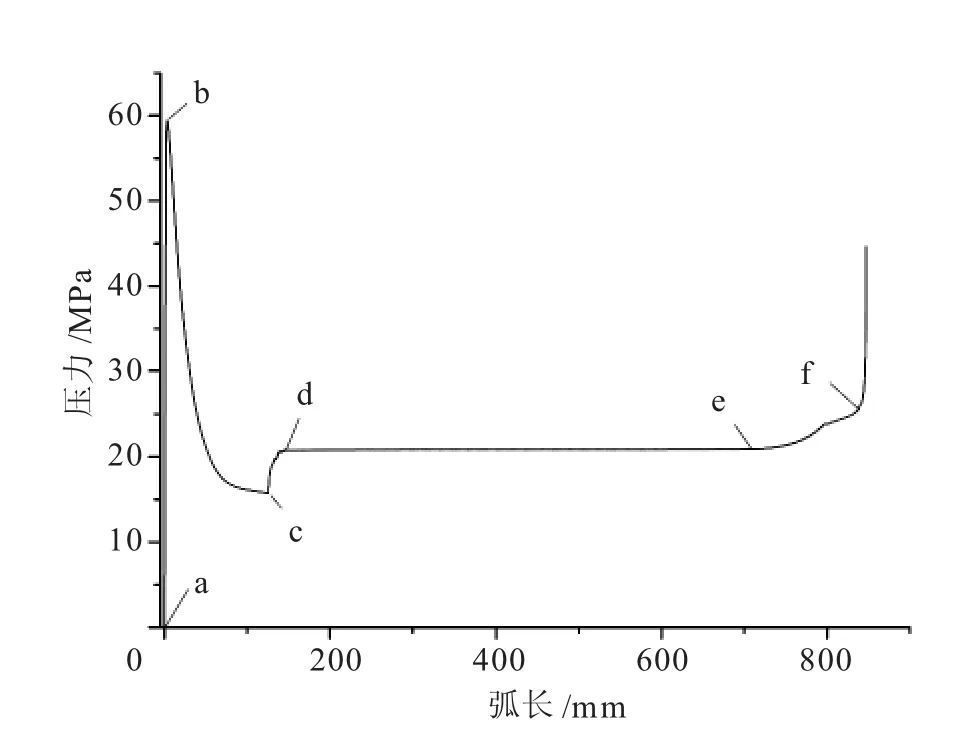
图4 计算得到的外部压力随弧长变化曲线

图5 系统压溃和屈曲扩展过程/MPa

从图5可以看出，管子初始形状见图5（a）；引发压溃的压力峰值的形状见图5（b），该压力峰值（压溃压力）与管子初始几何缺陷密切相关，初始几何缺陷越小，峰值越大。该峰值对扩展屈曲压力影响较小；峰值之后出现压力下降段，压力极小值对应的形状见图5（c），此时出现内壁接触；之后压力会有所增加，开始屈曲扩展，达到屈曲扩展稳定压力时的形状见图5（d）；之后屈曲扩展稳定压力直到图5（e）；最后由于管子边界约束而压力增加，求解结束，最终形状见图5（f）。

有限元模拟所得屈曲扩展压力及规范公式计算屈曲扩展压力结果见表1。

表1 屈曲扩展压力计算结果比较

2 有限元模拟结果与规范比较

DNVGL-ST-F101及API-RP-1111等海底管道系统规范均给出了屈曲扩展校核准则，对不满足规范准则的海底管道需安装止屈器，其间距依据费用和备用管子原则确定[17-18]。

2.1 DNVGL-ST-F101准则

在外压超过下面给出的准则（适用于15＜D/t2＜45）情况下，需安装止屈器，扩展屈曲准则表达为：

式中：Pe为外部压力，MPa；Pmin为最小内部压力，MPa；Ppr为屈曲扩展压力，MPa；fy规定最小屈服强度，MPa；αfab为制造系数；γm为材料抗力系数；γSC，LB为安全等级抗力系数；t2为特征壁厚，mm；D为钢管外径，mm。

2.2 API-RP-1111准则

屈曲扩展压力在下式条件下应安装止屈器。

式中：P0为外部静水压力，MPa；Pi为管内压，MPa；fp为屈曲扩展设计系数；Pp为屈曲扩展压力，MPa；S为规定最小屈服强度，MPa；t为钢管名义壁厚，mm；D为钢管外径，mm。

DNVGL-ST-F101屈曲扩展校核准则适用于径厚比为15＜D/t2＜45的管道；而对于超出规范公式适用范围的小径厚比（D/t2≤15）管道，需要采用数值模拟、模型试验等方法验证。有限元模拟是进行小径厚比深水管道屈曲扩展校核的简单有效方法。本文对径厚比范围10≤D/t2≤45深水海底管道进行了扩展屈曲有限元模拟，得到了管道压溃压力和屈曲扩展压力，并与DNVGL-ST-F101、API-RP-1111进行对比。有限元模拟时，除管道壁厚外，其他管道几何模型、材料非线性本构模型、初始几何缺陷、约束条件等均与前文算例相同。屈曲扩展压力与径厚比D/t关系见图6。

图6 屈曲扩展压力与径厚比D/t关系

分析表明，海底管道屈曲扩展压力有限元模拟值与DNVGL-ST-F101相吻合，当径厚比15≤D/t2≤45时，有限元模拟结果较规范公式计算结果偏大，偏差不超过3%；当径厚比10＜D/t2＜15时，有限元模拟结果比规范公式计算结果仍偏大，偏差超过3%，但不超过5%。说明在进行深水海底管道屈曲扩展压力计算时，尽管DNVGL-ST-F101明确屈曲扩展压力计算公式适用范围15＜D/t2＜45，但对于超出该规范且径厚比为10＜D/t2≤15时，仍可按规范值初步估计管道屈曲扩展压力，并按本文方法进行有限元模拟分析。

3 结论

基于ABAQUS软件进行了深水海底管道屈曲扩展有限元分析。有限元模拟采用Riks法求解，考虑了Ramberg-Osgood材料非线性、接触非线性和求解几何非线性，模拟了在初始椭圆度缺陷情况下深水海底管道压溃、屈曲扩展过程。通过海底管道屈曲扩展有限元模拟得到了管道屈曲扩展压力与径厚比D/t的关系，并与DNVGL-ST-F101和API-RP-1111规范值进行比较，表明有限元模拟所得不同径厚比D/t的海底管道屈曲扩展压力与DNVGL-ST-F101规范值相吻合，即使对DNVGL-ST-F101超出规范公式适用范围的小径厚比D/t2≤15的情况同样如此，表明在小径厚比条件下DNVGL-ST-F101屈曲扩展公式仍然适用。