基于Autodesk Maya的虚拟织物悬垂性评价因子分析

周 琦,杜宇轩,张 辉

(北京服装学院,北京100029)

nCloth[1]是三维动画设计软件Autodesk Maya中专门用于制作虚拟织物或服装的模块。在该模块中,可以通过调节虚拟织物的动力学参数(Dynamic Properties),改变虚拟织物或服装在模拟仿真时的悬垂形态,从而模拟各种不同类型的虚拟面料或服装。但nCloth模块所提供的预设面料参数有限,对于日常服装和面料,设计师只能凭感觉和经验进行调节,与真实面料或服装往往会有一定的差异。为了能够更好地在Autodesk Maya环境下模拟织物与服装,本文在前期工作[2]的基础上,采用因子分析法将17个描述虚拟织物悬垂性能指标综合为少数几个因子,简化虚拟织物悬垂性评价体系,为在Autodesk Maya环境中进行虚拟织物或服装的模拟研究提供一定的帮助。

1 虚拟织物悬垂性能试验

在前期研究的基础上,确定了对虚拟织物悬垂形态影响显著的6个动力学参数,分别是拉伸阻力、压缩阻力、弯曲阻力、弯曲角度衰减、质量和阻尼。进行分段取值,其他动力学特性参数固定为系统预设值,共得到1 728个试验组合。6个动力学参数取值见表1。在Autodesk Maya环境下进行虚拟织物悬垂性模拟试验,见图1。

织物的悬垂性是指织物因自重下垂而形成自然曲面的性能,它主要影响织物的保形性和视觉风格,是面料服用性能设计的重要组成部分。织物的悬垂性描述指标有很多,主要分为悬垂程度指标、悬垂形态指标两大类。本研究利用张辉博士研发的软件Draping Testor,测量虚拟织物的17个悬垂性描述值[3-5],即:悬垂系数、波纹数、投影面积、投影周长、形状因子、平均波峰夹角、波峰夹角不均匀率、平均波谷夹角、波谷夹角不均匀率、方位差、方位不对称度、平均峰高、峰高不均匀率、平均谷高、谷高不均匀率、平均峰宽、峰宽不均匀率。

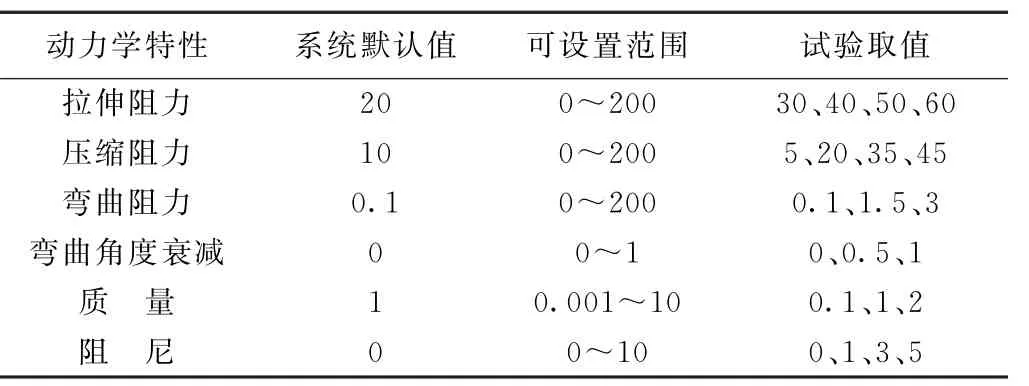
表1 虚拟织物主要参数取值

图1 Autodesk Maya环境下的虚拟织物悬垂性模拟试验示意图

2 虚拟织物悬垂性评价指标的因子分析

因子分析方法旨在将相关性比较密切的若干个变量归结为一个因子,以较少的几个因子反映整体的主要特征信息,它最早是由英国心理学家C.E.斯皮尔曼提出[5-6]。因子分析的主要应用有两个方面:一是探寻评价体系的基本结构,简化变量系统;二是找出若干个起支配作用的主因素,从而根据因子得分值对变量或样本进行分类。进行因子分析,可以简化试验数据分析,又能全面且客观地表达虚拟织物的悬垂性,为简化虚拟织物悬垂性与Autodesk Maya系统内的动力学参数关系的研究提供依据。

2.1 相关性分析

相关系数是描述两者间线性关系强弱程度和方向的统计量,取值在1和-1之间,绝对值越大说明两者之间相关性越高。使用SPSS软件对试验得到的1 728组数据进行处理,得到17个悬垂性描述指标间的相关系数矩阵[7]。相关系数矩阵中的大部分系数绝对值都大于0.3,即变量之间大多存在相关性。通过分析发现,除投影周长、平均峰宽、峰宽不均匀率外,大部分变量间的相关系数绝对值均大于0.3。其中,除悬垂系数、波纹数、投影周长、波峰夹角不均匀率、方位差、平均峰高、谷高不均匀率、平均峰宽、峰宽不均匀率间的相关系数绝对值小于0.8外,其他变量均与这9个变量存在较强的相关性。相关分析结果表明,能够从中提取公共因子,适合进行因子分析。

2.2 因子分析

使用SPSS的“降维”功能模块进行因子分析,得到悬垂性描述指标相关系数矩阵的初始特征值和累积方差贡献率,相关系数矩阵的初始特征值见表2。

在因子分析中,选取因子的原则是根据变量的公共因子方差占总方差份额,选取其中最大的k个,一般由前k个公共因子所对应的特征值之和占全部特征值的累积百分数大于85%确定(k小于变量个数)。分析表2,前4个因子的累积贡献率达到85.720%,达到要求。因此利用这4个公共因子来整合原来的17个虚拟织物悬垂性指标,能比较全面地反映所有信息。经过因子旋转后得到的新公共因子的累积方差贡献率见表3。

2.3 因子载荷矩阵及命名

为了解释找到的4个因子,需要对因子载荷矩阵进行旋转。利用SPSS软件,采用Kaiser标准化的正交旋转法,得到旋转后的因子载荷表,见表4。

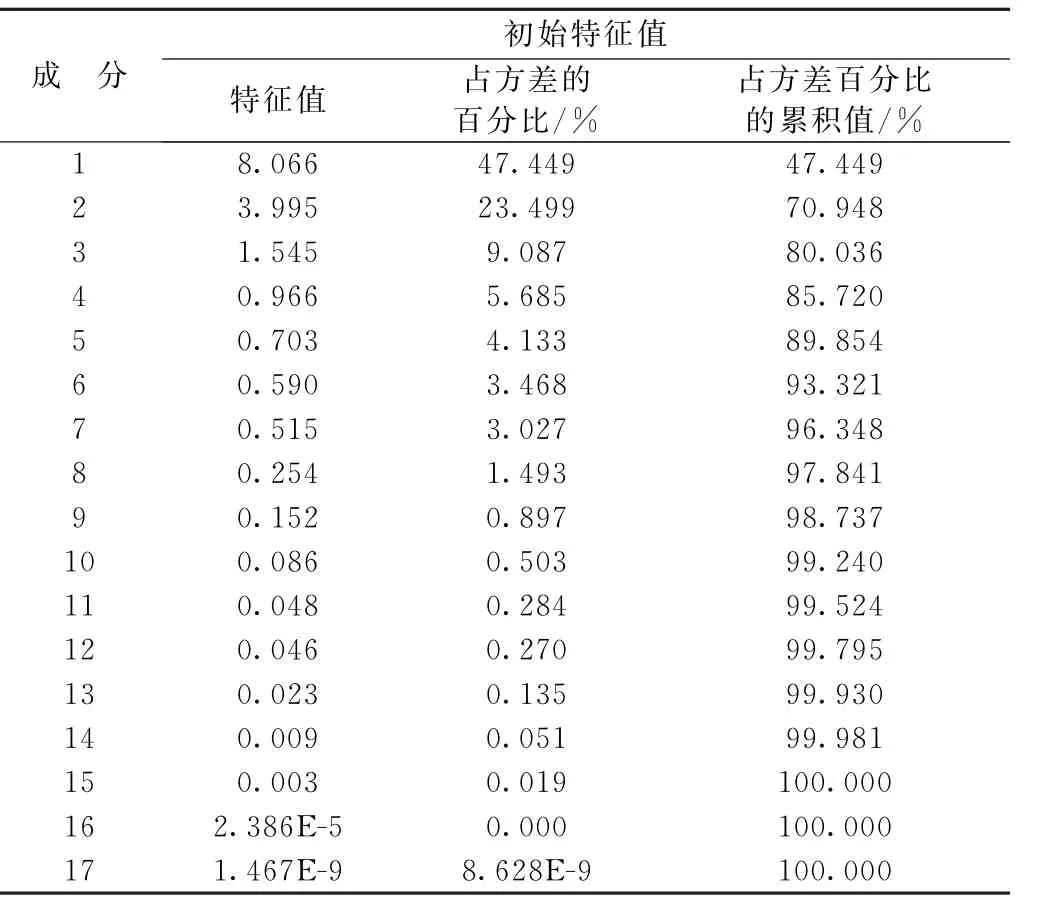
表2 相关系数矩阵的初始特征值

表3 因子旋转后的累积方差贡献率

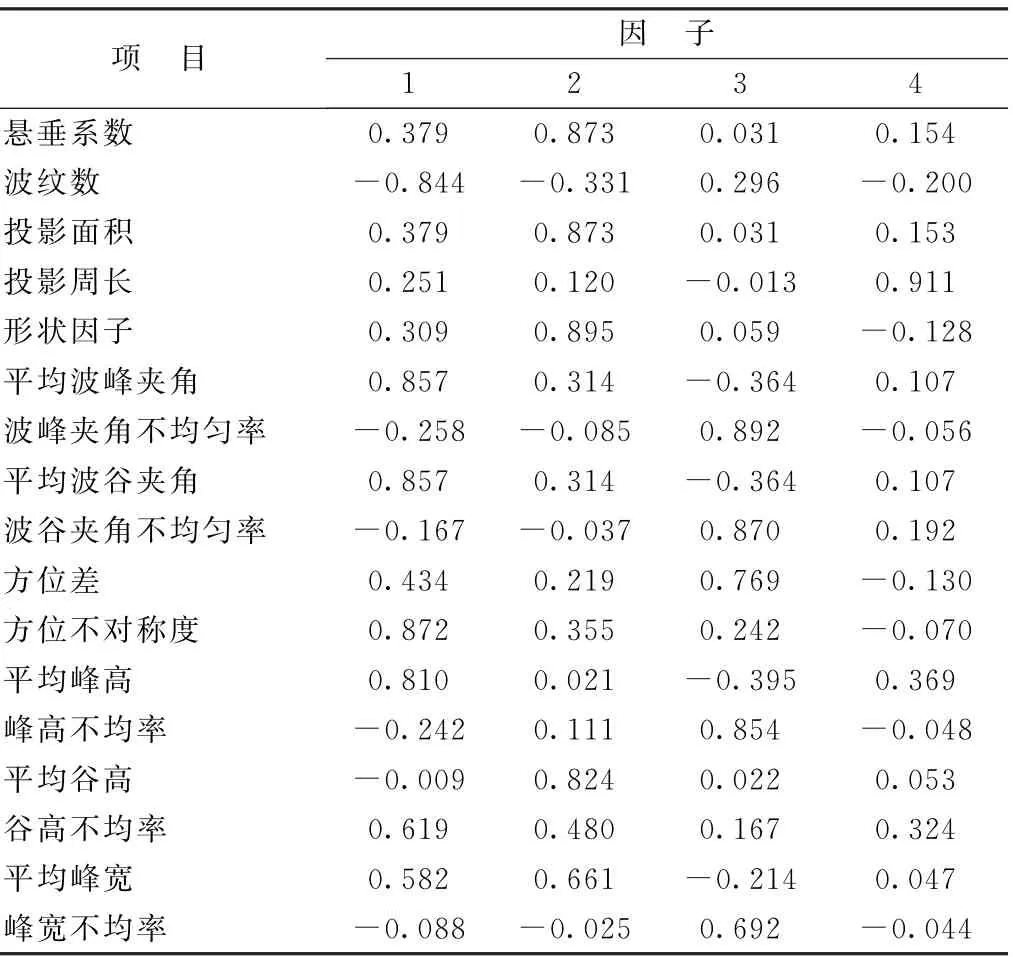
表4 旋转后因子载荷表

由表4可知,每个因子只有少数几个悬垂性描述值的因子载荷较大,可据此命名4个因子:因子1主要与波纹数、平均波峰夹角、平均波谷夹角、方位不对称度、平均峰高关系密切,反映了织物投影的形状特点,因此因子1可命名为悬垂形态因子;因子2主要与悬垂系数、投影面积、形状因子、平均谷高关系密切,反映了织物悬垂程度,因此因子2可命名为悬垂程度因子;因子3主要与波峰夹角不均匀率、波谷夹角不匀率、峰高不均匀率、方位差关系密切,反应织物投影的不均匀程度,因此因子3可命名为悬垂不均匀因子;因子4主要与投影周长关系密切,而在面料不发生弹性变形的情况下,投影周长应保持恒定,因此因子4可命名为悬垂变形因子。

3 结语

使用Autodesk Maya进行虚拟织物的悬垂性试验,测量出虚拟织物的17个悬垂性描述值,再对试验结果进行分析。通过因子分析法,将描述虚拟织物悬垂性的17个指标综合为4个因子,即:悬垂形态因子、悬垂程度因子、悬垂不均匀因子、悬垂变形因子。这4个因子的累计贡献率达到85.72%,在试验数据分析简化的基础上,较好地反映了虚拟织物的悬垂性信息,实现了因子分析的目的。