递增二次约束混沌系统基于圆判据观测器的同步*

赵友男 ， 章 伟 ， 宋 芳

（1.上海工程技术大学智能控制和机器人实验室，上海 201620；2.华中科技大学教育部图像处理与智能控制重点实验室，湖北 武汉 430074）

0 引 言

混沌是一种存在于非线性系统中的特殊现象。由于它对初始条件的高度敏感性，混沌在保密通信等领域有着较好的应用。近年来，作为混沌保密通信基础的混沌同步，已经成为这一领域的研究热点。Pecora和Carroll[1]最早使用驱动响应的方法研究混沌同步。之后，很多研究者提出了很多不同的混沌同步方案[2-4]。

随着非线性系统观测器的研究深入，研究者们提出了很多基于观测器的混沌同步与控制方案[5-7]。Boutayeb等人[8]为一类满足Lipschitz条件的混沌系统提出了一种一般的基于观测器的混沌同步。杨俊起和朱芳来[9]使用一种步进滑模观测器实现了混沌同步。Cherrier等人[10]设计了滑模观测器，实现了带有未知输入的混沌系统的同步。王划等人[11-12]研究了带有未知参数的统一混沌系统的有限时间同步问题。

观测器可以产生渐近趋近于系统状态的估计值。最初，Thau[13]介绍了一种用于Lipschitz非线性系统的保证观测器误差渐近稳定的条件。之后，很多观测器设计方案被提出[14-15]。近些年，满足单边Lipschitz条件的非线性系统的观测器成为一个热门领域[16]。这主要是由于用于单边Lipschitz非线性系统的观测器在Lipschitz常数较大时也能表现出较好的性能。这一点要优于传统的Lipschitz非线性系统的观测器。最近，D’Alto和Corless[17]提出了一种满足递增二次约束（Incremental Quadratic Constraint，δQC）的非线性系统观测器。δQC为多种常见的非线性系统提供了统一的描述，也就是说，很多常见的非线性约束条件如Lipschitz条件[18]、扇形有界条件[19]和单边Lipschitz条件[20]都是δQC的一种特例。满足δQC的非线性系统的观测器的存在条件已经被提出[21]。Chakrabarty等人[22]研究了在δQC非线性系统存在有界的外部输入时的观测器设计问题。

受到文献[23]的启发，本文主要为满足δQC的非线性系统设计了一种圆判据观测器，并且使用此观测器实现了基于观测器的混沌同步。由于δQC为多种常见的非线性系统提供了统一描述，本文的混沌同步方案适用于多种常见混沌系统。

文章安排如下：第1节介绍预备知识和系统的模型；第2节设计基于观测器的混沌同步；第3节进行仿真验证；第4节总结全文。

1 系统描述和递增二次约束

考虑如式（1）所示的一类混沌系统：

统一混沌系统可以由以下形式描述[11]：

当α∈[0,1]时，这个系统是混沌的；当α=0时，系统简化为原始的Lorenz系统；当α=1时，系统变为原始的Chen系统。上述统一系统可以写为式（1）的形式，其中：

Liu系统的方程为[24]：

当a=10，b=40，k=1，c=2.5，h=4时，系统有一个混沌吸引子。上述系统写成式（1）的形式，其中：

下面将给出关于递增二次约束（δQC）[17]条件的如下定义。

定义1[21]：一个对称矩阵 M ∈是向量值非线性函数f(q)的一个递增乘数矩阵，当且仅当f(q)满足如式（12）所示的递增二次约束条件：

递增乘数矩阵M为向量值非线性函数f(q)刻画了一种具有递增意义的性质。实际上，很多常见的非线性函数满足δQC条件。

例如，假设f(q)满足Lipschitz条件，即存在某个标量γ＞0，使不等式：

递增乘数矩阵M为：

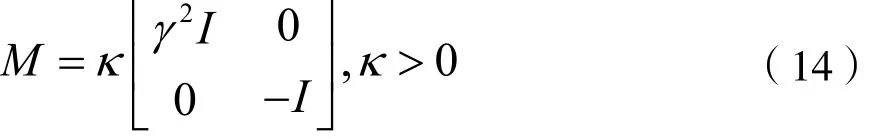
再如，当f(q)满足单边Lipschitz条件[16]时，即存在某个ρ∈R，有：

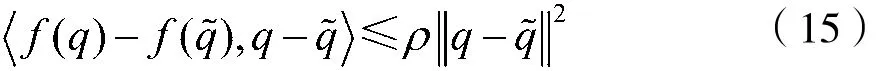
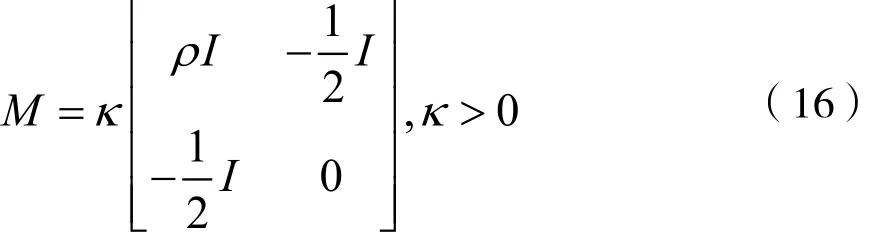
混沌是一种经常出现在非线性系统中的现象。很多混沌系统是满足δQC的。例如，Bloch系统[25]：

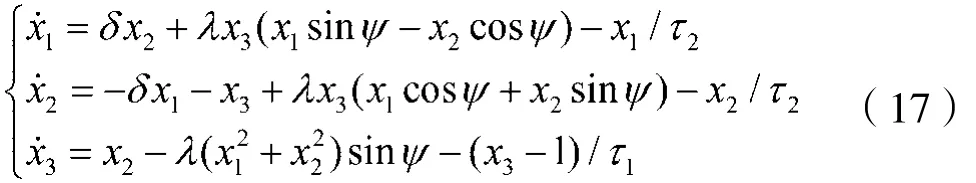
其中 δ=-0.4π，λ=30，Ψ=0.173，τ1=5，τ2=2.5。然后，这个系统可以改写为：

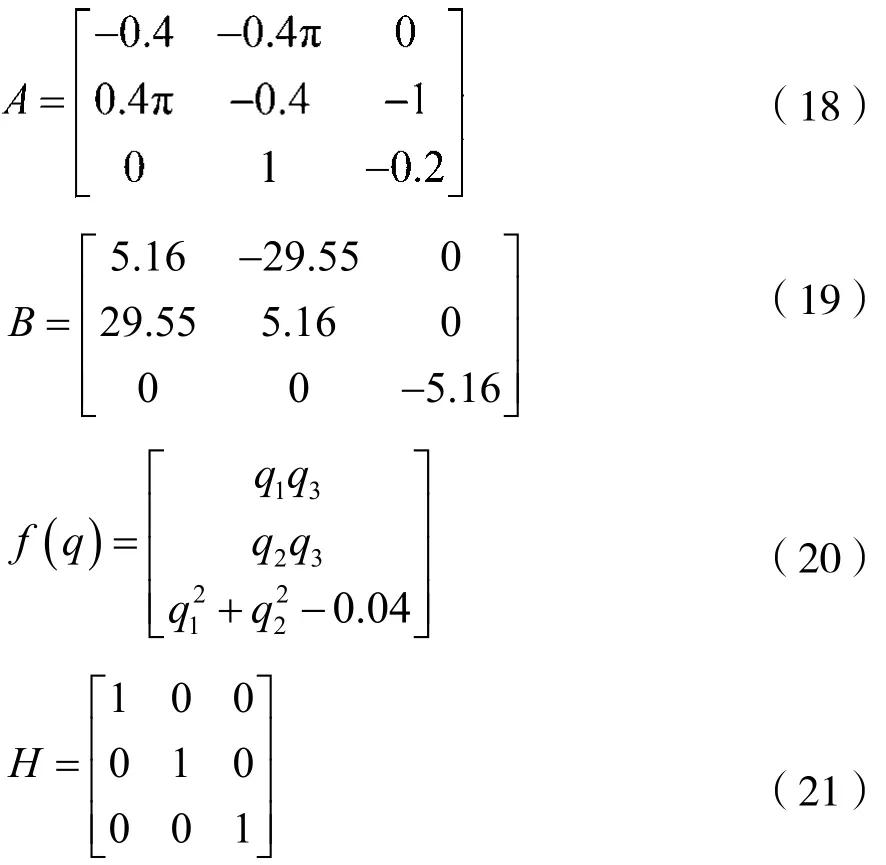
Bloch系统的非线性部分属于与文献[17]中的多胞体情形（Polytope Case）。根据文献[17]中的结论，通过求解线性矩阵不等式，可以得到递增乘数矩阵：

2 系统描述和观测器设计

本节考虑一种具有线性输出的混沌系统模型：

构造一种基于圆判据的观测器：

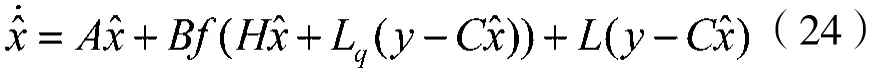
定理1：假设混沌系统满足δQC，其中递增乘数矩阵M满足式（25）的形式且M22≤0，M11＞0。若对于某个已知的α＞0，存在矩阵P=PT＞0，Lq、R使线性矩阵不等式：

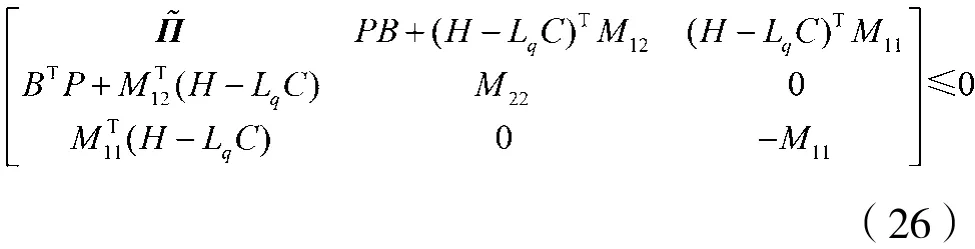
成立，其中：

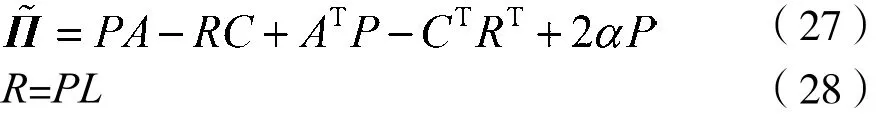
则式（28）是系统的指数稳定观测器，其中增益矩阵L=P-1R。对于所有的t＞0都有状态值误差e(t)满足：

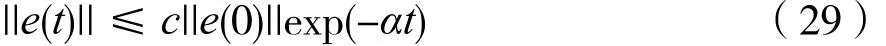
证明：系统的状态误差动力学方程为：

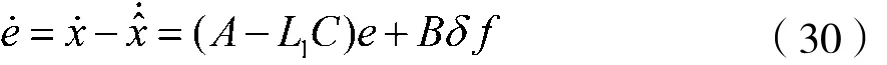
其中：

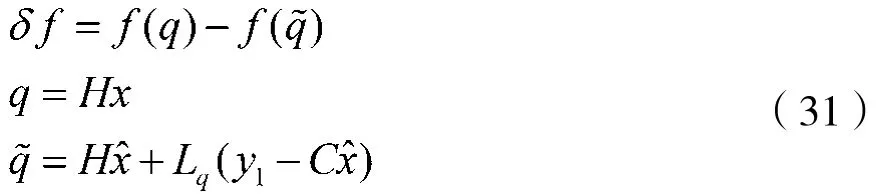
根据式（4）和式（12），可得：

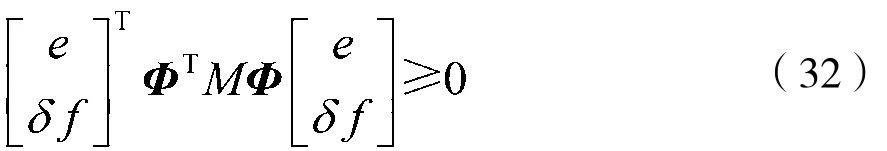
其中Φ由式（16）给出。选择V(e)=eTPe作为Lyapunov函数，V沿着状态轨迹的时间导数为：

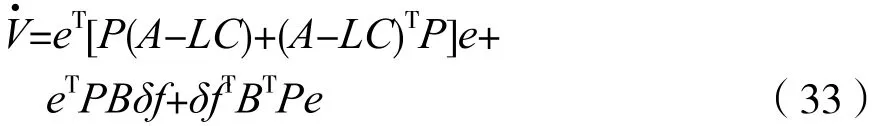
由于M11＞0，用Schur补引理可以将不等式（10）写成如下形式：

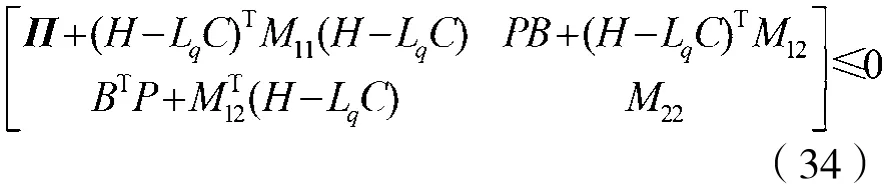
其中：

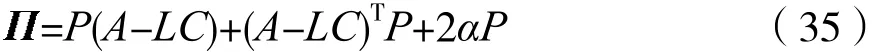
显然，有解的一个必要条件是M22≤0。

记：

不等式（15）可以改写成如下形式：

因此，用[eTδfT]及其转置分别左右乘不等式（37），结果为：

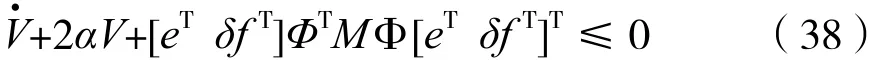
由不等式（13）和不等式（18）可得：

利用比较引理（见文献[26]的定理3.4），可知：

结合：

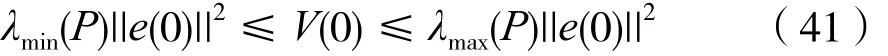
可得：

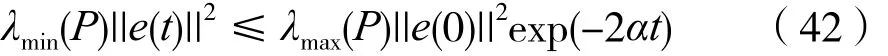
因此：

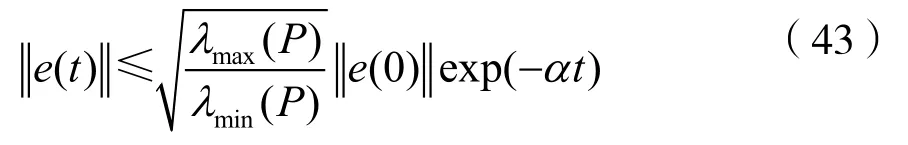
3 仿真实例

在这一章节，通过一个实例来展示观测器系统的同步效果。这里选取第2节中使用的例子Bloch系统作为本章的仿真实例。

设系统的线性输出为：

这个系统可以改写为：

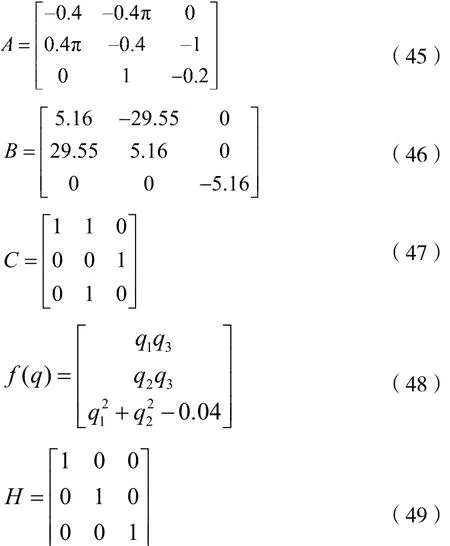
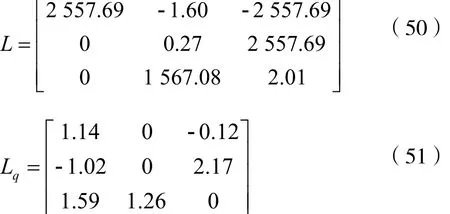
根据第2节的例子，f(q)满足δQC且M由等式（22）给出。使用第3节的定理1，求解得到的观测器的增益矩阵为：

当初值为x(0)=[0 0 0]、x(0)=[8 -10 12]时，图1展示了Bloch系统的混沌吸引子，图2展示了观测器产生的估计值与实际值的误差衰减的曲线。综合图1和图2可以看出，尽管Bloch系统的非线性现象十分复杂，但是设计的混沌同步方案使观测器系统和混沌系统之间的估计误差在很短的时间内以指数速率收敛到0，实现了系统间的同步。仿真结果说明，提出的基于圆判据观测器的混沌同步方案是可行的。

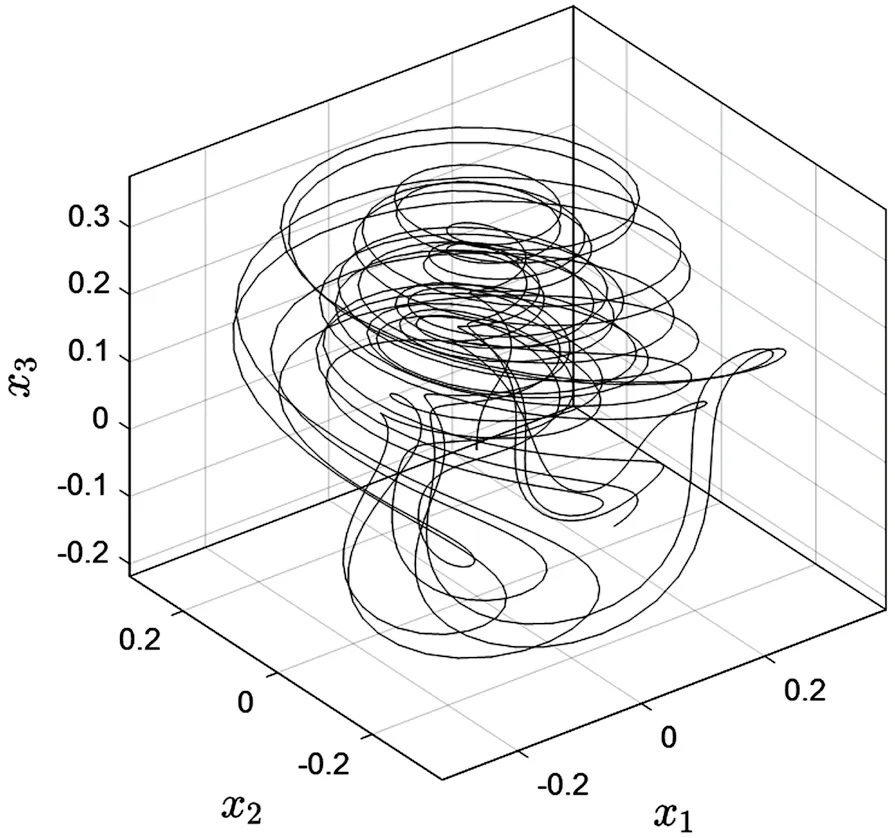
图1 Bloch系统的混沌吸引子

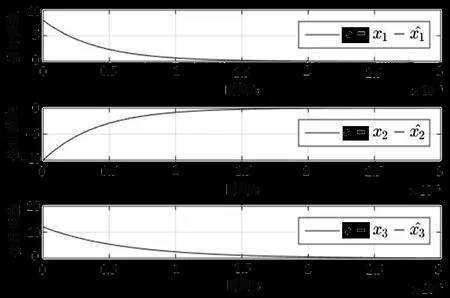
图2 观测器的估计误差e

4 结 语

本文为满足递增二次约束（δQC）条件的非线性系统设计了一种圆判据观测器，并将这种观测器用于混沌同步。因为δQC条件为很多常见的非线性系统提供了一种统一的描述形式，相比于传统的混沌同步方案，所以本文的同步方案可以适用于多种不同的混沌系统。此外，观测器存在的充分条件由线性矩阵不等式给出，易于求解。观测器的估计误差以指数速率收敛到0，实时性好。仿真的结果表明，该混沌同步方案的有效性。后续工作会考虑在系统中增加有界的外部扰动，即在非线性系统中添加未知输入，并对系统的进行鲁棒控制，或者设计自适应控制方案。