干密度对生物质垃圾炉渣力学特性的影响

张 攀，徐永福

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

随着经济的发展，城市垃圾日益增多。其主要处理方式为填埋、焚烧、堆肥等。由于成本、技术等原因，中国仍然主要采用焚烧方式。该方法需重点考虑对环境的影响，尽量实现废物再利用。固体垃圾焚烧的主要产物为粉煤灰和炉渣。粉煤灰已被广泛应用于混凝土和煤矿充填，炉渣可作为工业陶瓷中的催化烧结剂，在土木工程中可替代骨料作为路基填筑材料。

国内外对于炉渣的研究取得了较多的成果。XIE等[1]分析了炉渣的物理化学特性，评估了其作为路基材料的可行性。LE等[2]通过三轴固结排水试验测定了炉渣的黏聚力、内摩擦角、变形模量等基本力学参数。冯兴波等[3]对城市垃圾炉渣进行了无侧限抗压强度试验,分析了不同干密度试样在不同龄期下的强度特性。徐永福[4]通过三轴试验研究了生活垃圾炉渣在饱和状态下的强度特性，并提出可以通过大、小主应力之间的关系确定炉渣的抗剪强度参数。宋丹青等[5]研究了含水率对生活垃圾炉渣强度的影响，发现炉渣在最优含水率附近具有最大抗剪强度。张远博等[6]采用离散元软件PFC 3D对垃圾炉渣的力学性质进行了模拟，分析了其应力-应变关系，探讨了边界刚度对剪切强度参数和压缩模量的影响，为炉渣的研究提供了一种新思路。

目前针对炉渣力学性能方面的研究多侧重于原材料、颗粒级配、应力状态等因素对其强度与变形特性的影响。而实际上粗粒料的力学响应不仅取决于应力状态，还与密实程度有关，因此本文主要分析干密度对炉渣强度及变形特性的影响。

1 试验方案

1.1 试验材料

试验用炉渣取自江苏省南通市垃圾焚烧厂，原状炉渣呈灰色颗粒状，形状各异，通过筛分试验，得到如图1所示的颗粒级配曲线。粒径大于1 mm的粗粒约占60%，不均匀系数为21，级配良好。炉渣矿物成分主要为石英、石膏、方解石、微斜长石以及磁铁矿，其中石英含量46%。炉渣中主要氧化物为CaO，SiO2，Fe2O3，SO3，总含量高达70%，见表1。

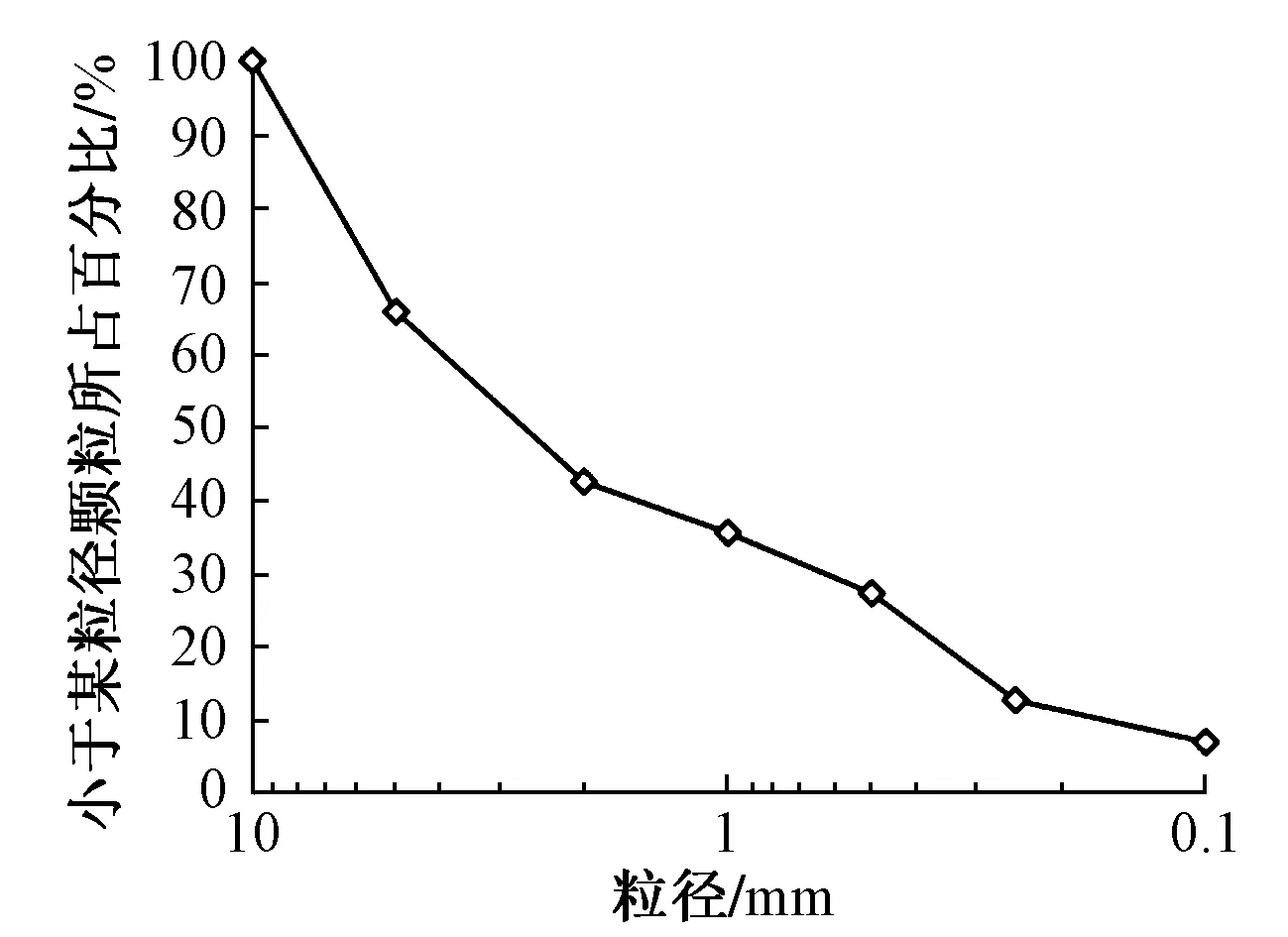
图1 炉渣颗粒级配曲线

表1 炉渣中氧化物

1.2 试验方法

将粒径小于2 mm的炉渣加水拌合至含水率为22%，塑料袋密封12 h。根据不同干密度称取相应质量的炉渣，在试样模中分5层击实，试样高度80 mm，直径39.2 mm。文献[2]提出炉渣三轴试验剪切速率最好控制在0.009～0.144 mm/min，本试验剪切速率控制在0.055 mm/min。本文在3种干密度(0.9,1.0,1.1 g/cm3)下开展三轴固结排水试验，每一种干密度下进行3组试验，围压分别为50,100,200 kPa。

2 试验结果与分析

2.1 应力-应变关系

参考临界状态土力学，三轴试验中当应变超过20%时，试样的应力分布已经不均匀，应力-应变曲线关系出现失真，因此本文取炉渣应变20%段进行分析[7]。炉渣的应力-应变曲线见图2。图中纵坐标为大、小主应力差σ1-σ3，横坐标为竖向应变εa。在低围压(50，100 kPa)下炉渣应力-应变曲线大多呈应变软化型，有明显的峰值强度，而在高围压下(200 kPa)应力-应变曲线呈硬化型。松散炉渣应力-应变曲线呈现硬化特性，紧密炉渣应力-应变曲线软化特征明显。炉渣应力-应变曲线特性由围压和干密度共同决定，紧密炉渣在高围压下也可能出现应变硬化。

图2 炉渣的应力-应变曲线

2.2 峰值强度

不同围岩下炉渣的峰值强度(σ1-σ3)max随干密度ρd变化曲线见图3。可见：随着干密度的增加，峰值强度也随之增大，但其增长幅度明显减小。在低围压下峰值强度相对较小，且其增长幅度明显比高围压时低。如围压200 kPa时干密度由0.9 g/cm3增加到1.0 g/cm3，峰值强度增加了176 kPa，而围压50 kPa时仅增加了76 kPa。这主要是因为相同围压下干密度越大颗粒之间孔隙越小，排列越紧密，嵌入咬合作用越明显，在剪切变形过程中能承受较大的应力，峰值强度高；初始干密度一定时，围压越大试样压缩变形越大，相对密实度提高导致强度明显增大。因此，炉渣的峰值强度不仅与围压有关，还与干密度紧密相关。

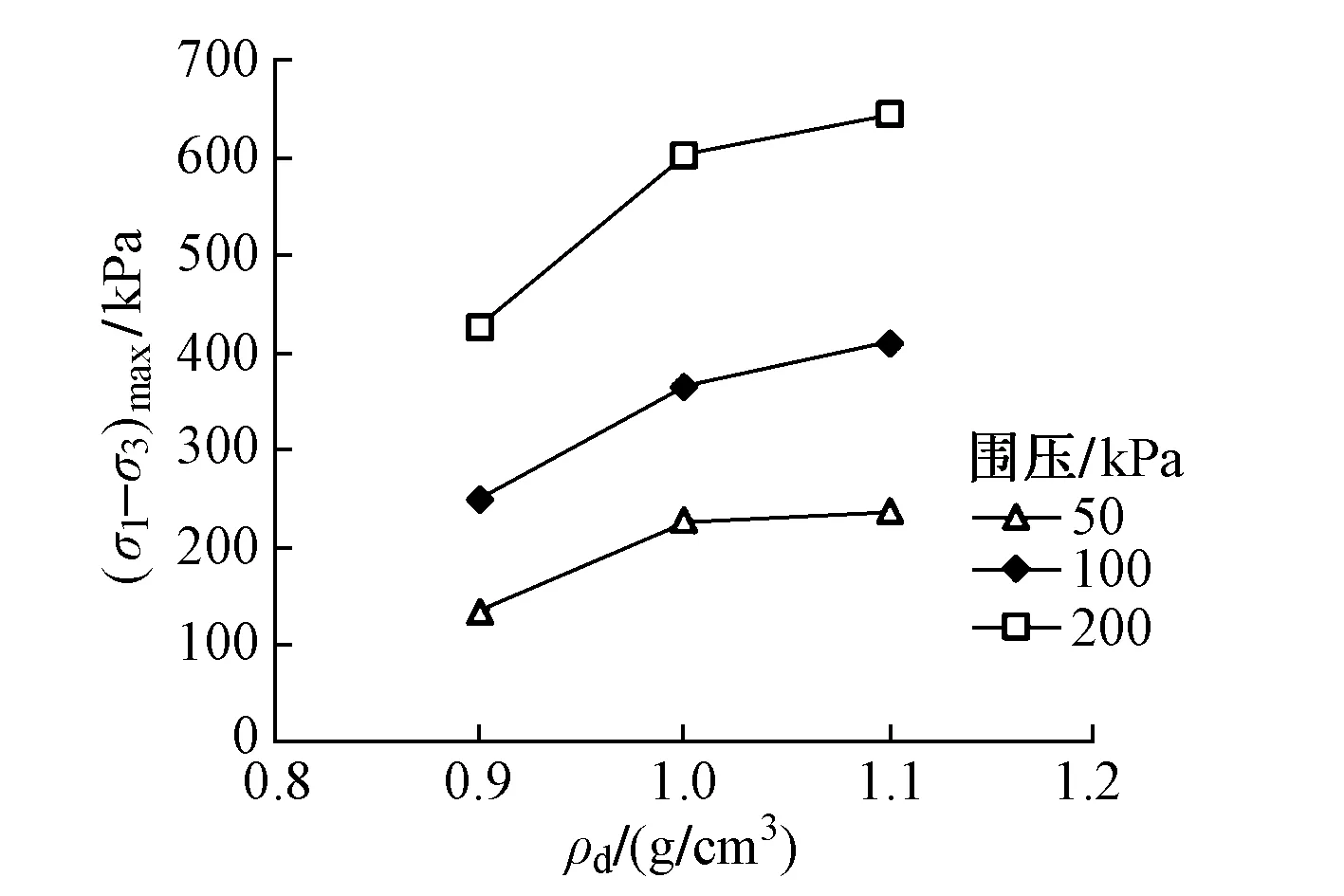
图3 不同围岩下炉渣的峰值强度随干密度变化曲线

2.3 初始弹性模量

不同围压下炉渣的初始弹性模量Ei随干密度ρd变化曲线见图4。可见：初始弹性模量随着干密度的增大而增大，如围压50 kPa、干密度由0.9 g/cm3增至1.0 g/cm3时，初始弹性模量从62 kPa增至114 kPa，增幅84%。同时，围压越大初始弹性模量亦越大，但其影响远小于干密度，如干密度为0.9 g/cm3，围压从50 kPa提高到100 kPa时，初始弹性模量从62 kPa 提高到74 kPa，增幅仅19%。这主要是因为干密度越大颗粒排列越紧密，剪切过程中竖向能承受较大荷载，而围压对于初始弹性模量的作用未充分发挥出来，干密度起主要作用。在相同荷载作用下初始弹性模量越大变形越小，因此采用炉渣填筑路基时可以提高干密度，增大初始弹性模量，从而减小路基变形。

图4 不同围压下炉渣的初始弹性模量随干密度变化曲线

2.4 抗剪强度

根据摩尔-库仑定律可以得到抗剪强度表达式。

式中：c为黏聚力;φ为内摩擦角。

若纵坐标t=(σ1-σ3)/2，横坐标s=(σ1+σ3)/2，对不同围压下求得的σ1，σ3进行拟合，则拟合直线的斜率为sinφ，与纵坐标的截距为c·cosφ。

干密度为0.9 g/cm3时炉渣的抗剪强度可由图5确定。同样方法可求得其他2种干密度下炉渣的抗剪强度，结果见表2。可见：随着干密度的增加，黏聚力和内摩擦角均增大。这是因为炉渣干密度越大孔隙比越小，固体颗粒之间的胶结咬合作用越强，致使黏聚力和内摩擦角提高。

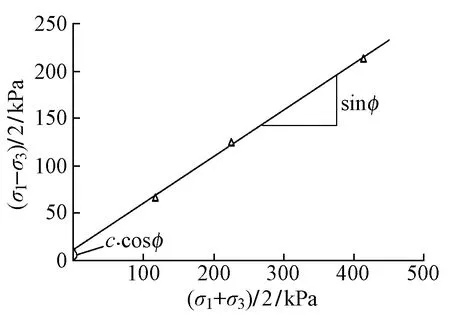
图5 干密度0.9 g/cm3时炉渣的抗剪强度确定

表2 不同干密度下炉渣的抗剪强度

3 结论

本文对不同干密度的炉渣进行了三轴固结排水试验，得到如下结论：

1)生活垃圾炉渣的力学特性不仅与其应力状态有关，还与干密度密切相关。

2)松散炉渣应力-应变曲线呈现硬化特性，紧密炉渣应力-应变曲线软化特征明显。

3)初始弹性模量随着干密度的提高而增大，用炉渣路基填筑时可以适当提高干密度以减小变形。

4)随着干密度的增大，炉渣的黏聚力和内摩擦角也有所提高，但变化幅度较小。