型钢混凝土钢架等效弹性模量研究

于 丽，杨 涅，吕 城，王明年，童建军

(1.西南交通大学 土木工程学院,四川 成都 610031;2.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031)

隧道开挖后为控制围岩应力适量释放和围岩变形，同时也为了增加结构的安全度和方便施工，往往需要施作初期支护。初期支护通常采用锚杆喷射混凝土支护，必要时可采用钢纤维喷射混凝土或配合使用钢筋网、钢架等[1]。在初期支护体系中，型钢钢架由于具有刚度大、架设后受力快、对围岩能够迅速提供支撑作用等特点[2]，因此在变形较大的软弱围岩隧道中应用广泛。初期支护提供的支护压力主要受弹性模量的影响，因此有必要对型钢混凝土钢架等效弹性模量进行研究。

目前对于等效弹性模量的研究主要基于静力载荷试验方法和细观力学方法。静力载荷试验方法直观、原理简单，但费事、费时、代表性不强和难以全面检测[3]；而细观力学方法，理论计算较为准确，但在工程实际中，得出的结果不一定可靠，也缺乏试验数据的支撑[4]。

因此在实际工程中，对于型钢混凝土组合结构的等效弹性模量，往往按照JGJ 138—2016《组合结构设计规范》的有关规定进行计算，即对于轴向受力构件，按等效轴向刚度公式计算;对于弯曲受力构件，按等效弯曲刚度公式计算。针对于隧道中的型钢混凝土钢架，单位长度可视为偏心受压短柱，其等效弹性模量的取值理论上应介于等效轴向刚度和等效弯曲刚度的计算值之间，因此有必要对不同受力状态的型钢混凝土构件等效弹性模量计算方法进行研究。

型钢混凝土是一种复合材料，与钢筋混凝土结构配筋率类似，其截面面积比(型钢截面面积/构件截面面积)的变化也影响其弹性模量的取值，进而影响结构的力学性能、动力特性。在目前已进行的配筋率对钢筋混凝土构件弹性模量影响的试验中，证明了配筋率对钢筋混凝土结构的弹性模量有明显影响，弹性模量与配筋率基本呈线性关系。类似的，型钢混凝土构件若忽略此影响，对结构的分析会造成较大的误差[5-6]。

因此本研究以型钢混凝土短柱的截面面积比为变量，分别基于等效轴向刚度原理和等效弯曲刚度原理，计算了型钢混凝土短柱在轴压、受弯情况下的等效弹性模量解析解，将其与有限元方法的数值解进行比较，验证其一致性，并利用有限元方法求得了偏心受压情况下的等效弹性模量，探讨了其等效弹性模量计算方法。

1 求解等效弹性模量的解析法

型钢混凝土构件的变形取决于刚度，保证构件等效前后的刚度不变，即可得到钢筋混凝土构件的等效弹性模量。对于轴向受力构件，应以等效轴向刚度相等为原则，确定等效弹性模量；对于受弯构件，则应以等效弯曲刚度相等为原则。相应的计算公式如下[7]：

EA=EcAc+EaAa

(1)

EI=EcIc+EaIa

(2)

式中：EI,EA分别为构件截面抗弯刚度和轴向刚度；EcIc,EcAc分别为混凝土部分的截面抗弯刚度和轴向刚度；EaIa,EaAa分别为型钢的截面抗弯刚度和轴向刚度。

2 求解等效弹性模量的有限元方法

不同受力状态下型钢混凝土构件等效弹性模量的取值，轴向受力构件、受弯构件可分别采用式(1)、式(2)的计算方法。对于偏心受压构件，其等效弹性模量的取值应介于二者之间。由于偏心受力构件的等效弹性模量按等效轴向刚度原理和等效弯曲刚度原理计算，均与实际状况不完全相符，因此这里采用ANSYS有限元方法求解出不同受力状态下型钢混凝土短柱的等效弹性模量，方法如下：

1)设计短柱尺寸、荷载以及约束条件。

2)建立不同截面面积比下型钢混凝土短柱的分离式模型，如图1(a)所示。由于只考虑弹性范围，故不考虑型钢和混凝土间的黏结滑移，这样型钢和混凝土之间就可以通过共用相同的节点来协调位移和力的传递。选用Solid 45单元模拟混凝土和型钢[8-9]，计算构件的变形Δ1。

3)将构件视作各向同性的弹性体，建立型钢混凝土构件的整体式模型，如图1(b)所示。选用Solid 45 单元建模，输入初始弹性模量E0，计算构件的变形。

图1 型钢混凝土有限元模型

4)调整E0的大小重新代入上一步模型中，计算构件变形Δ2，最终使Δ2=Δ1，则等效弹性模量即为此时输入的E0。

选择轴压、弯曲、偏压3种基本受力状态的型钢混凝土短柱，受力状态通过调整轴力N和弯矩M的大小来实现，计算模型如图2所示，尺寸统一设定为300 mm×300 mm×1 000 mm，材料相关参数如表1所示，型钢选用刚性钢架常用的10～20号工字钢[10]，即设8种截面面积比。

图2 计算模型示意(单位：mm)

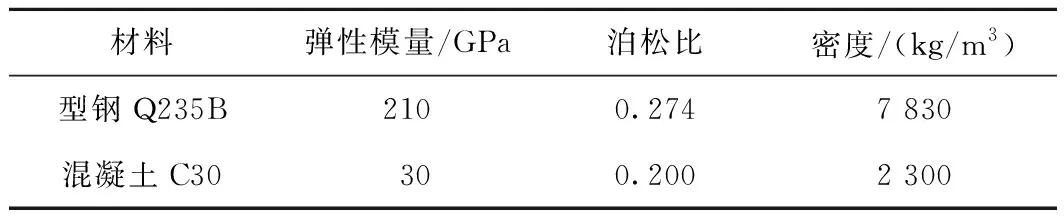
表1 材料参数

2.1 轴向受压柱的等效弹性模量

轴向受压柱模型的加载方式如图2(a)所示，其中N=90 kN(以面荷载形式分布)，弹性模量有限元数值解荷载为E0，由式(1)得出解析解为E。将计算结果绘制成散点图，进行线性拟合得到拟合曲线，见图3。并计算出解析解与数值解的相对误差，见表2。

图3 轴向受压柱的等效弹性模量计算值

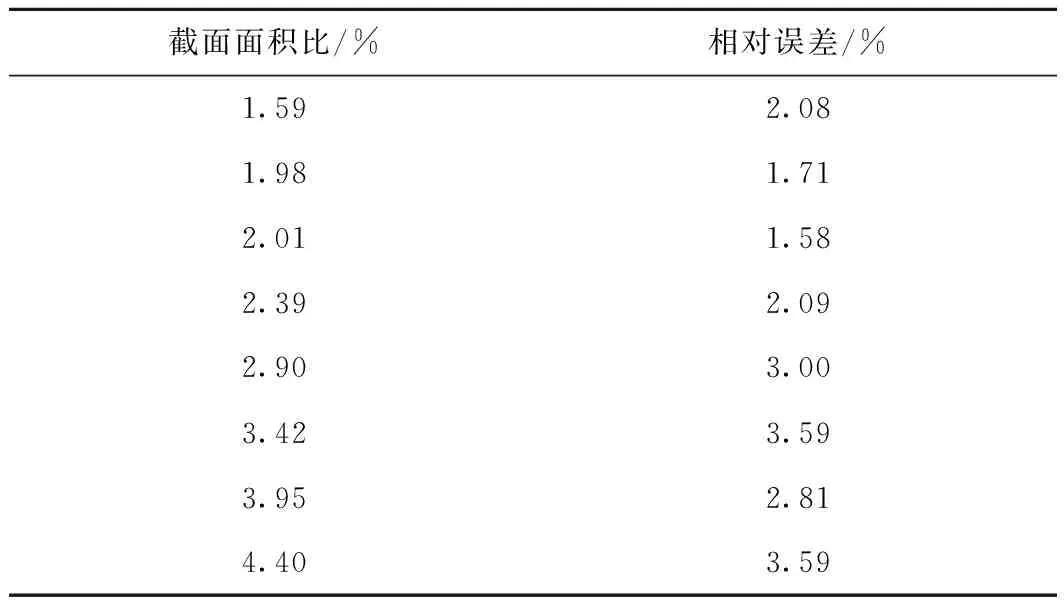
表2 轴向受压柱的等效弹性模量解析解与数值解的相对误差

由图3及表2可知，无论是有限元方法还是解析法，等效弹性模量与截面面积比之间都基本呈线性关系。当截面面积比较小时，构件的解析解与数值解之间相差较小；随着截面面积比的增加，解析解与数值解的差值逐渐增大，最大相对误差为3.59%，误差较小。因此，在型钢钢架常用的截面面积比范围内，解析法与有限元方法计算结果有较好的一致性，轴向受压构件可采用等效轴向刚度的弹性模量解析式(1)计算其等效弹性模量。

2.2 受弯柱的等效弹性模量

受弯柱模型的加载方式如图2(b)所示，其中变矩M=3.6 kN·m(以力偶形式给出)，弹性模量有限元数值解为E0，由式(2)得出解析解为E。将计算结果绘制成散点图，进行线性拟合得到拟合曲线，见图4。并计算出解析解与数值解的相对误差，见表3。

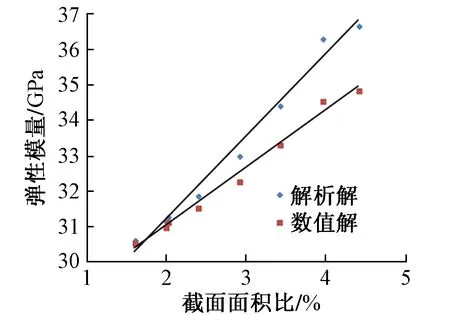
图4 受弯柱的等效弹性模量计算值

表3 受弯柱的等效弹性模量解析解与数值解的相对误差

由图4及表3可知，无论是有限元方法还是解析法，等效弹性模量与截面面积比之间都基本呈线性关系。当截面面积比较小时，构件的解析解与数值解之间相差较小；随着截面面积比的增加，解析解与数值解的差值逐渐增大，最大相对误差为5.21%，误差仍较小。因此，在型钢钢架常用的截面面积比范围内，解析法与有限元方法计算结果有较好的一致性，采用等效弯曲刚度的弹性模量解析式(2)计算受弯构件的等效弹性模量能取得较好的精度。

2.3 偏心受压柱的等效弹性模量

偏心受压柱模型的加载方式如图2(c)所示，其中N=90 kN(以面荷载形式分布)，M取不同的值(以力偶形式给出)，计算得到偏心距e为0，5，10，20，40，80，150 mm及∞(N=0，M≠0)时不同截面面积比对应的等效弹性模量数值解(其中e=0对应轴向受压柱；e=∞ 对应受弯柱)，并由式(1)得出轴向受压柱的解析解、由式(2)得出受弯柱的解析解。将计算结果绘制成散点图，并拟合出不同偏心距下偏心受压柱等效弹性模量的线性拟合曲线，见图5。

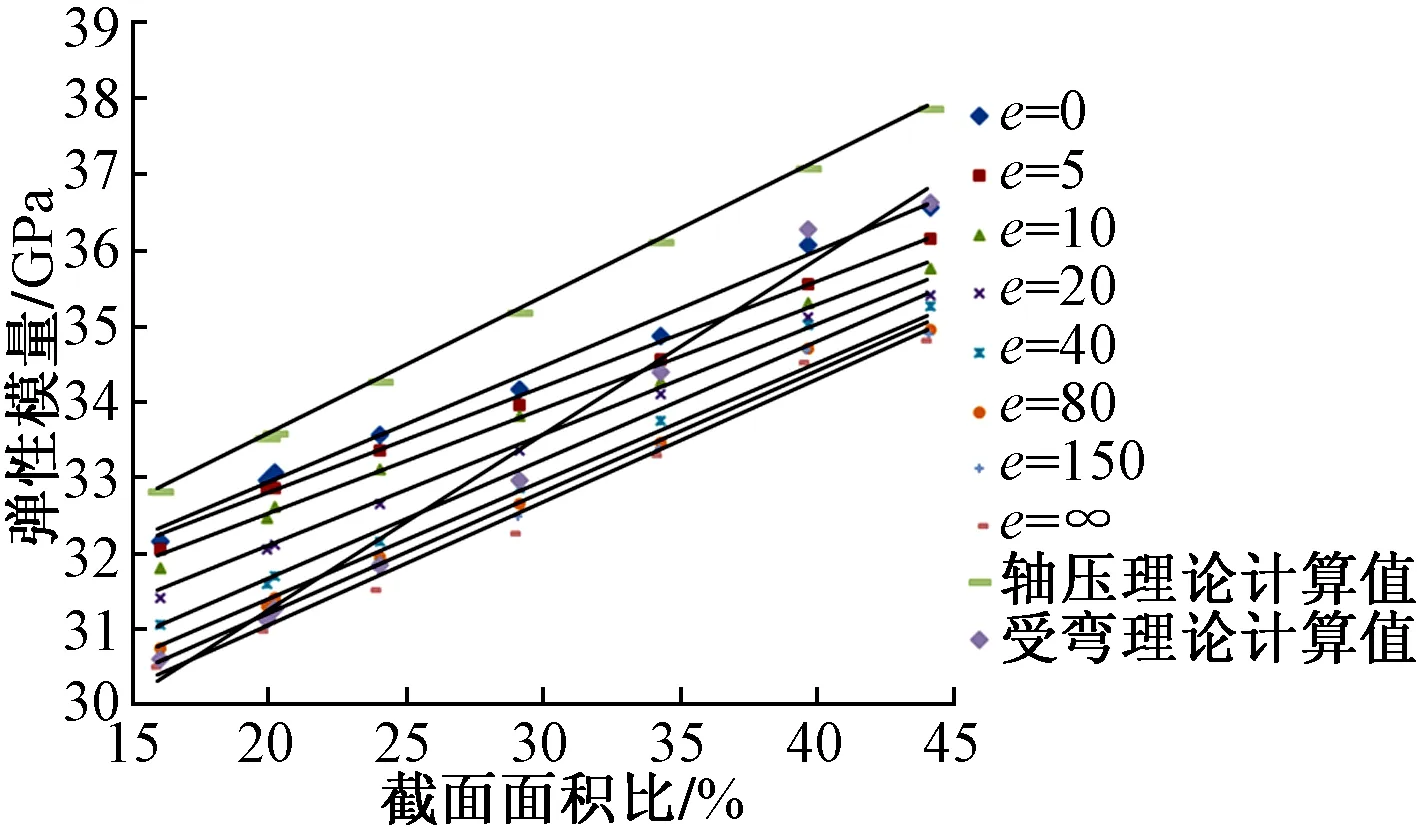
图5 不同偏心距下的等效弹性模量

由图5可知，不同偏心距下等效弹性模量与截面面积比之间仍基本为线性关系。随着偏心距的增大，偏心受压柱的等效弹性模量拟合直线的斜率逐渐增大，从轴向受压柱(e=0)逐渐偏向受弯柱(e=∞)。当偏心距e>80 mm 时，偏心受压柱的等效弹性模量拟合曲线与受弯柱基本一致。

并根据不同相对偏心距e/h下，随截面面积比的变化，弹性模量的数值解与解析解的相对误差的大小，并选择误差较小的解析法为最佳解法，如图6所示。

图6 不同相对偏心距(e/h)下随截面面积比的变化弹性模量的最佳解析法

由图6得出的结论见表4。

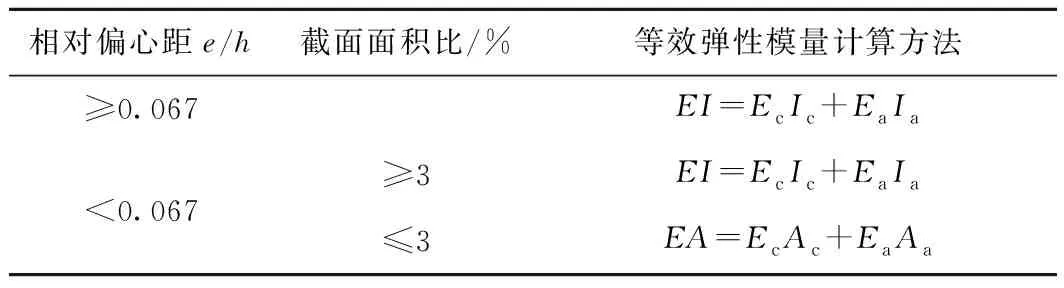
表4 不同相对偏心距下等效弹性模量的计算方法

由表4可知：当相对偏心距≥0.067时，对于任意截面面积比，采用等效弯曲刚度的计算方法;当相对偏心距<0.067，截面面积比≥3时，采用等效弯曲刚度的计算方法，反之采用等效轴向刚度的计算方法。但此时，即使采用等效弯曲刚度的计算方法，数值解与2种解析解的相对误差均在5.50%以内，相对误差也均不大，因此，实际工程中可直接采用等效弯曲刚度计算型钢混凝土偏心受压柱等效弹性模量。

3 结论

本文基于解析法和有限元方法分析了型钢混凝土轴向受压柱、受弯柱和偏压受压柱的截面面积比对其等效弹性模量的影响，得到以下结论：

1)不同受力状态型钢混凝土短柱的等效弹性模量与截面面积比之间基本呈线性关系；

2)对于轴向受压柱、受弯柱，用等效轴向刚度和等效弯曲刚度原理得出的等效弹性模量具有较好的精度，在实际工程中可直接采用；

3)对于偏心受压柱，可直接采用等效弯曲刚度计算其等效弹性模量。