梁式倾角传感器在桥梁状态长期监测中的应用
2018-11-07李志伟黄茂忠李明乐
李志伟,黄茂忠,李明乐
(1.北京铁科首钢轨道技术股份有限公司,北京 102206;2.中国铁道科学研究院 铁道建筑研究所,北京 100081;3.河北航科工程检测设备技术有限公司,河北 衡水 053000)
至2017年底,我国高速铁路运营里程已超过2万km,基于我国的国情及高速铁路建设特点,高速铁路设计多采取“以桥代路”的策略,桥梁总长占线路全部里程的比例最高达82%。如何管理好数量如此巨大的桥梁,及时发现高速铁路每一孔桥梁可能存在的隐患并加以排除,确保运营过程中每一孔桥梁时刻保持良好的工作状态,是高速铁路养护部门的一个长期而艰巨的任务。
高速铁路桥梁的荷载主要为静荷载,列车荷载所占比例很小,桥梁的工作状态如基础稳定性及其变化发展趋势、大跨度桥梁的挠曲变形状态及其发展等主要由静荷载或其他非荷载因素引起,因此,对高速铁路桥梁工作状态的监测可在无列车荷载下进行。由于桥梁数量巨大,选用的传感器除了必须具有精度高、零漂小、重复性和稳定性好、便于安装等优点外,同时还要求具有经济性上的可行性,能用于既有桥梁,可实现远程自动化数据采集与分析等功能。
传统上,对桥梁结构的评估通过人工目测检查或借助于便携式仪器测量得到的信息进行。但是人工桥梁检查方法在实际应用中有很大的局限性,对大量的高速铁路桥梁采用人工检查的方法难以实施。随着传感器、计算机和通讯等现代化技术的发展,近年来,建立和发展了桥梁结构健康监测与安全评估系统,用以监测和评估桥梁运营期间结构的承载能力、运营状态、耐久能力等,极大地拓展了桥梁检测领域,增强了对桥梁运营安全的预测和评估能力。
桥梁健康监测用传感器主要有3类:第1类用以监测桥梁结构局部特征,如振弦式应变计、光纤传感器、测力计等;第2类用以监测桥梁结构的位置状态,如位移计、GPS、倾角仪、全站仪[1];第3类用以监测桥梁的环境因素,如风速仪、温度计、湿度计、雨量计等。根据有关资料,目前健康监测的费用巨大,高速铁路所有桥梁均采用此种方法进行监测在经济上是不可行的。
1 高速铁路桥梁安全监测技术思路
由于高速铁路桥梁列车荷载占总荷载的比例很小,其对梁桥的受力和变形影响也很小,桥梁运营安全主要取决于桥梁的位置状态是否正常。如果桥梁发生基础沉降或倾斜、挠曲变形过大等将影响线路的平顺性,危及高速列车的运营安全。因此,对高速铁路桥梁运营安全的长期性监测可转化为对其位置、状态的监测,掌握其位置、状态的发展变化趋势,及时发现问题,提前预警。
目前,关于墩台相对沉降的监测方法主要有水准仪测量法[2]、GPS测量法、连通管法等。水准仪测量法不宜用于大量、长期的沉降监测;GPS测量法精度和稳定性满足不了要求;连通管法需要布设连通管并注入液体,其优点是测试精度高,缺点是需要布设长管道,安装麻烦,维护困难等。
桥梁的相对位置状态还可应用倾角传感器进行测试[3]:对于简支箱形梁桥,可用倾角仪监测桥墩之间或墩台之间的相对沉降或倾斜;对于超静定结构桥梁,基础的相对沉降、倾斜或梁的挠度曲线可通过均匀分布于沿梁长方向的多台倾角仪的斜率测试,经积分和曲线拟合得出位移时程曲线,据以分析桥梁的工作状态[4],可尽早掌握桥梁的位置、状态。
1.1 基于倾角传感器的简支梁桥不均匀沉降监测
如果简支梁的跨度为L,在桥上无车的情况下,t1,t2时刻测得梁顺桥向的倾角为θ1和θ2,则在t2-t1时间段,相邻墩的相对沉降为
Δ=L(tgθ2-tgθ1)
连续测出一段线路各跨简支梁的相对沉降Δ,便可得出该段线路桥梁墩台在t2-t1时间段内的沉降曲线。
1.2 基于倾角传感器的梁挠曲变形模型的建立
数学理论证明了一条连续可导的曲线可以用多阶的幂函数近似表示。由于桥梁上部结构刚度很大,其挠曲线或位移曲线可以认为是连续可导的,可用n次的幂函数近似表示其位移方程
y≈a0+a1x+a2x2+…+anxn
(1)
对式(1)求导得斜率tgθ的方程。由于θ很小,位移方程任一点的斜率tgθ≈θ,得
(2)
如果实测出桥梁上部结构k个测点的k个转角θ1,θ2,…,θk,经曲线拟合得转角方程
θ=k1+k2x+…+knxn-1
(3)
对比方程(2)和(3)得出
(4)
由方程组(4)可得出a1,a2,…an。
检算荷载包括恒载和活载,恒载包括实心板梁、桥面铺装、栏杆等附属设施的自重。本次检算拟采用汽车-20级、挂车-100,人群荷载3.5 kPa作为检算荷载。
假设起始点x=0,位移y=0,则a0=0,将求得的a0~an代入计算式(1)即可得到桥梁上部结构相对于起始点的相对位移方程。
1.2.1 简支梁桥竖向位移方程的近似表示
简支梁在自重作用下的挠曲线方程是一个4次函数,即可用一个4次多项式来表示简支梁的挠曲线方程。由于梁的挠曲变形很小,如高速铁路的简支箱梁,挠跨比小于1/3 000,其挠曲线近似抛物线,一般用2次或3次函数便足以很精确表达简支梁的挠曲线方程,即:
y≈a0+a1x+a2x2
或y≈a0+a1x+a2x2+a3x3
(5)
上述两式中,如果a0=0,并且当x等于跨度L时y=0,多项式表示的是简支梁的挠曲线方程;如果a0≠0,或当x等于跨度L时y≠0,则方程所表示的是梁的相对位移方程,方程既包括梁的挠曲变形,也包含墩台的相对沉降。
1.2.2 连续梁桥竖向位移方程的近似表示
图1为3跨连续梁桥在自重作用下挠曲线形状,曲线共有4个反弯点,有周期曲线的特征。如果采用一个多项式函数来表达有4个反弯点的整条曲线,要达到较高的精度需要多项式的次数将较多。为了以较少次数的多项式函数较为准确表达连续梁竖向位移曲线,可充分利用Excel程序拟合曲线的便捷性,并对连续梁的位移曲线采用分段拟合的方法。

图1 连续梁挠曲变形图示
如图1所示,连续梁边跨的变形曲线只有1个反弯点,模拟数据分析和试验证明采用4次的多项式可以达到较高的拟合精度。
y边≈a0+a1x+a2x2+a3x3+a4x4
(6)
连续梁中跨的变形曲线有2个反弯点,采用5次或6次多项式也可以达到较高的拟合精度。
y中≈b0+b1x+b2x2+b3x3+b4x4+b5x5+b6x6
(7)
为了得到连续梁连续的竖向位移曲线,需建立相邻跨位移方程的联系,为此可令方程(6)和(7)共同支点处的位移相等,求出方程相关的常数项。
2 梁式倾角传感器
2.1 梁式倾角传感器的测试范围与精度
由于桥梁不容许有大的挠曲变形和墩台沉降,用于梁的竖向位移测试的梁式倾角传感器,其测量范围为±1°已经足够。
要较为准确地获得梁的挠曲变形和墩台的相对沉降状态,及时了解其发展变化趋势,倾角传感器必须具有足够的精度和稳定性。梁式倾角传感器的测试精度为0.002°,32 m跨简支梁墩台相对沉降的测试精度达到1.1 mm[5]。
2.2 数采设备与监测平台
数采设备包括前置器和远程测控站(Remote Teminal Unit,RTU)。数据采集、传输与监测分析平台工作流程如图2所示。

图2 数采与监测平台工作流程
监测平台是一个集数据采集、管理、分析、图形化显示、预报警等功能的监测平台软件,实施对桥梁沉降状态的长期监测。监测平台软件由客户端、服务器端、数据采集端3大功能模块构成。
3 应用试验
应用试验包括简支梁桥墩台不均匀沉降模拟试验和3跨连续梁桥梁的相对位移模拟测试试验2种。试验的目的是验证采用梁式倾角传感器测试桥梁上部结构相对位移的测试精度。本试验梁式倾角传感器的主要技术指标为:精度0.002°、重复性3‰、直线度4‰、零漂4‰、温漂4‰。
3.1 简支梁桥墩台不均匀沉降模拟测试试验
由于简支梁桥墩台发生相对沉降时梁的内力不发生变化,因此由墩台相对沉降产生的梁任何2点的倾角增量相同。测出梁发生的倾角增量为θ,则由此产生的相对沉降为
Δ=Ltgθ
图3为简支梁桥墩台不均匀沉降模拟测试试验装备。图中跨度L为 7 450 mm,右端支点进行2个循环试验,每个循环调高3次,倾角由左端支点处的梁式传感器进行测试,位移变化值由位于倾角传感器下方的百分表进行测量。试验测得梁的倾角增量及测试点的位移见表1所示。

图3 跨度7.45 m的简支梁试验
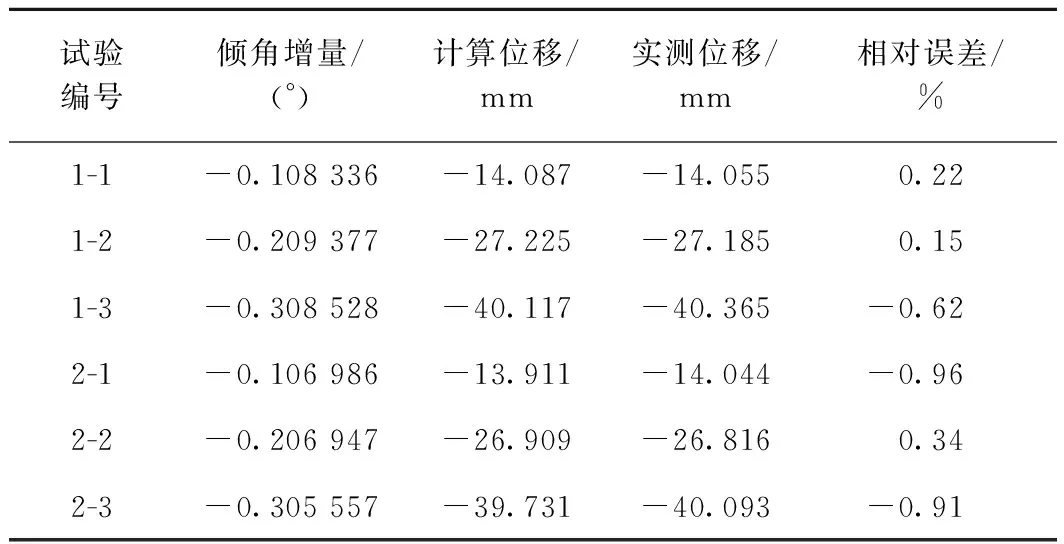
表1 简支梁支点沉降测试数据及误差计算
表1中,两组循环相对沉降试验得出的测点竖向位移计算值与实测值相对误差都小于1%,充分说明倾角传感器测试精度高,因此通过倾角计算得出的沉降量也得到高的精度。
3.2 3跨连续梁桥的相对位移模拟测试试验
3跨连续梁桥梁的相对位移模拟测试试验装备如图4所示。

图4 模拟梁、传感器整体布置及数据采集装置
模拟梁的跨度为(285+600+285)cm,模拟梁上共安装了14个倾角传感器,在梁的非支点处共安装了10个百分表,测试倾角传感器测试点处的竖向位移。
每个倾角传感器配一个前置器,安装于倾角传感器的封装盒中,各前置器串联至一个RTU远程测控站,并由远程测控站供电,前置器采集的数据由远程测控站通过GPRS无线网络发送至上位机。
试验荷载对称施加于模拟梁的中跨,使中跨的挠跨比达到1/1 000 左右。图5为试验测得的倾角曲线。图6为由倾角曲线积分和实测得到的位移曲线,可见计算得出的位移曲线与实测的位移曲线很接近,曲线形状与梁的变形相一致。表2为各位移测点的计算与实测竖向位移的比较,最大的相对误差为4.9%,这对于挠曲线的测试来说精度已经足够。

图5 倾角曲线
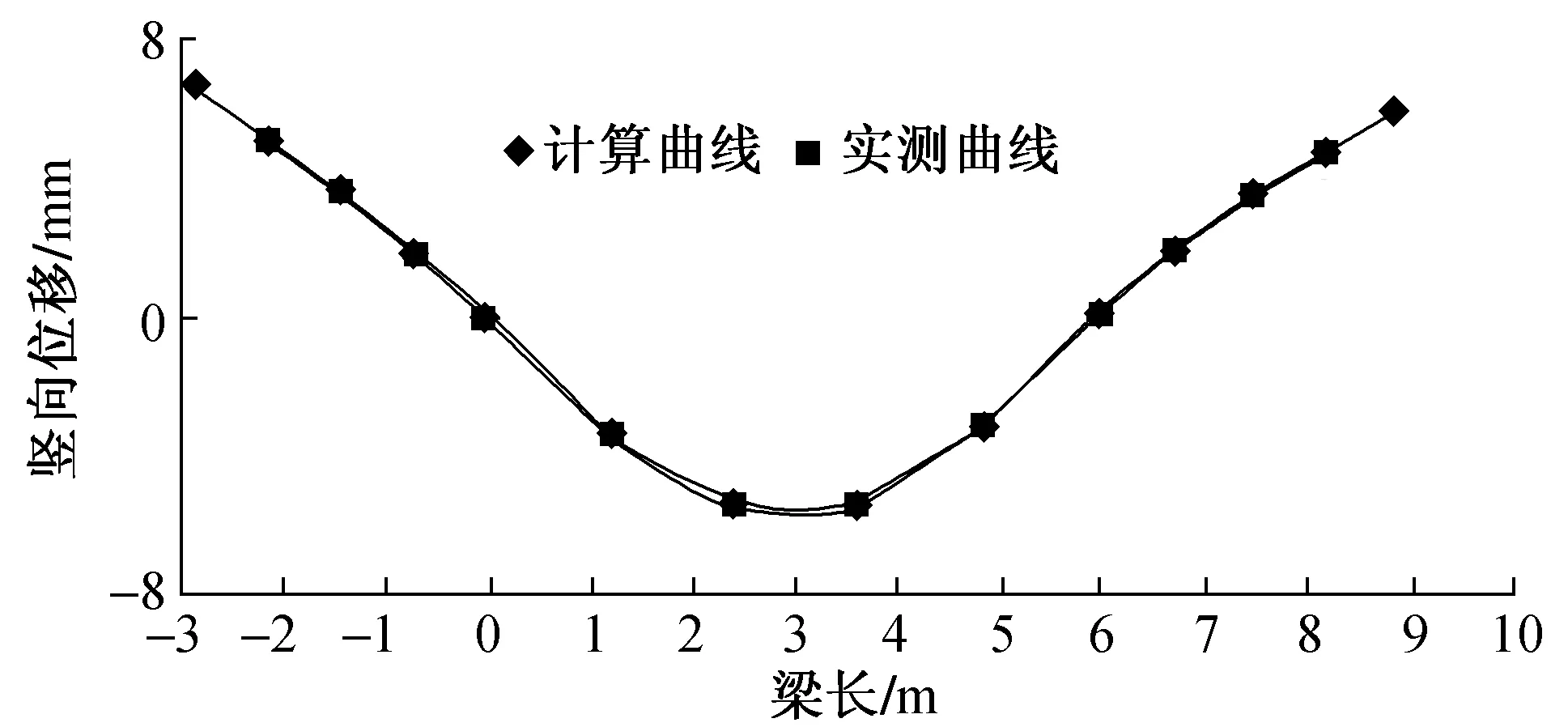
图6 位移曲线
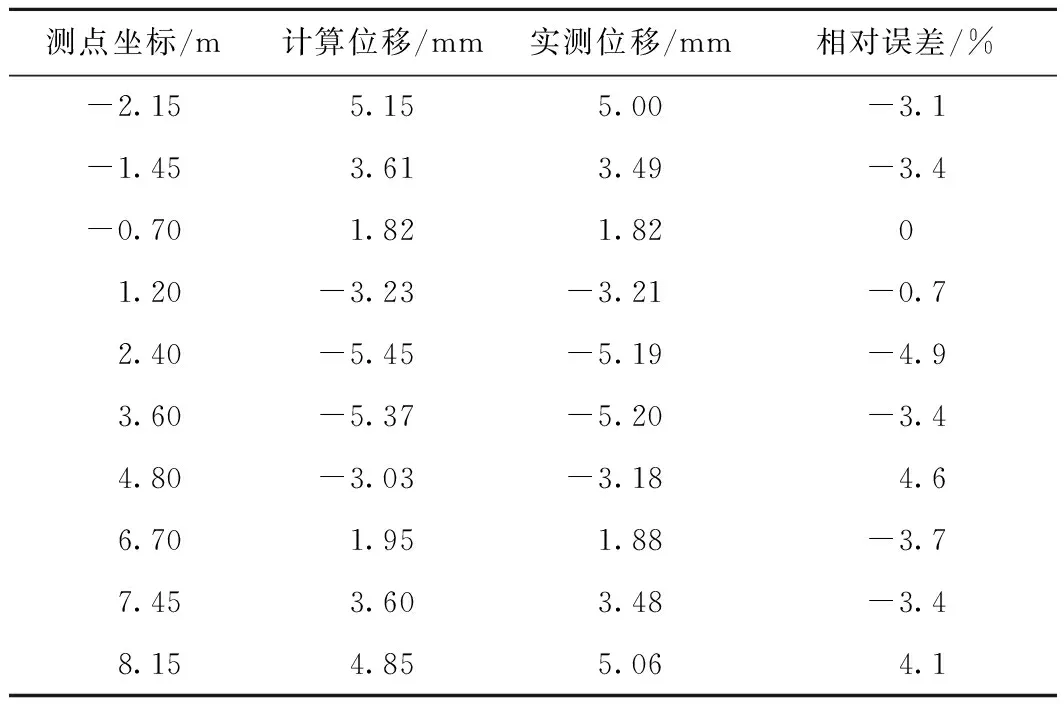
表2 连续梁相对位移测试数据及误差计算
4 结论
1)梁式倾角传感器具有足够的精度,可用以对墩台相对沉降和挠曲变形的长期监测。
2)各跨简支梁墩台的相对沉降构成了连续多跨简支梁桥的沉降曲线。
3)多跨连续的梁式结构,各跨的竖向位移曲线可用多阶的幂函数曲线表示,该幂函数曲线可由实测得到的切线方程积分得到。从第一跨至最后一跨,通过相邻跨共同支点的竖向位移相等,可建立跨与跨之间竖向位移的联系,从而得到上部结构的整个位移曲线。
