城市轨道交通直流牵引网稳态短路电流计算

李丹丹



城市轨道交通直流牵引网稳态短路电流计算

李丹丹

基于建立的整流机组外特性模型及牵引变电所、牵引网数学模型，利用电路图法求解单边供电和双边供电直流短路电路中的各个参数，推导直流侧牵引网单边供电和双边供电短路稳态模型中各牵引变电所供给的短路电流及短路点短路电流的表达式，并通过实例分析对直流牵引网稳态短路电流进行计算。

城市轨道交通；电路图法；稳态短路；单边供电；双边供电

0 引言

地铁供电系统直流侧短路电流计算是城市轨道交通工程中的一项重要内容，是牵引变电所设备选型、继电保护整定的重要依据[1]。直流牵引供电系统的短路电流由稳态和暂态短路电流分量2部分组成。稳态短路电流分量与线路电阻成反比，短路点越接近接触网末端，短路电流的值越小；对于暂态分量，短路瞬间的短路电流上升率最大，随着时间的延长，电流上升率按指数函数规律衰减，最终衰减为零。

自20世纪90年代以来，国内外开展了很多关于直流侧短路计算的研究。文献[2～4]对6脉波、12脉波和24脉波整流机组外特性曲线的分段线性化方法进行介绍；文献[5，6]对直流牵引网参数的求解方法进行介绍；文献[6～9]基于建立直流牵引供电系统数学模型对直流短路电流进行求解。

本文通过建立整流机组外特性模型、牵引变电所及牵引网的等效数学模型，对不同短路模型下各牵引变电所供给的短路电流及短路点的短路电流表达式进行推导，为直流短路稳态电流的计算提供基础，为工程设备选型提供依据。

1 直流牵引供电系统的组成

直流牵引供电系统由牵引变电所和牵引网2部分组成。图1为直流牵引供电系统示意图。

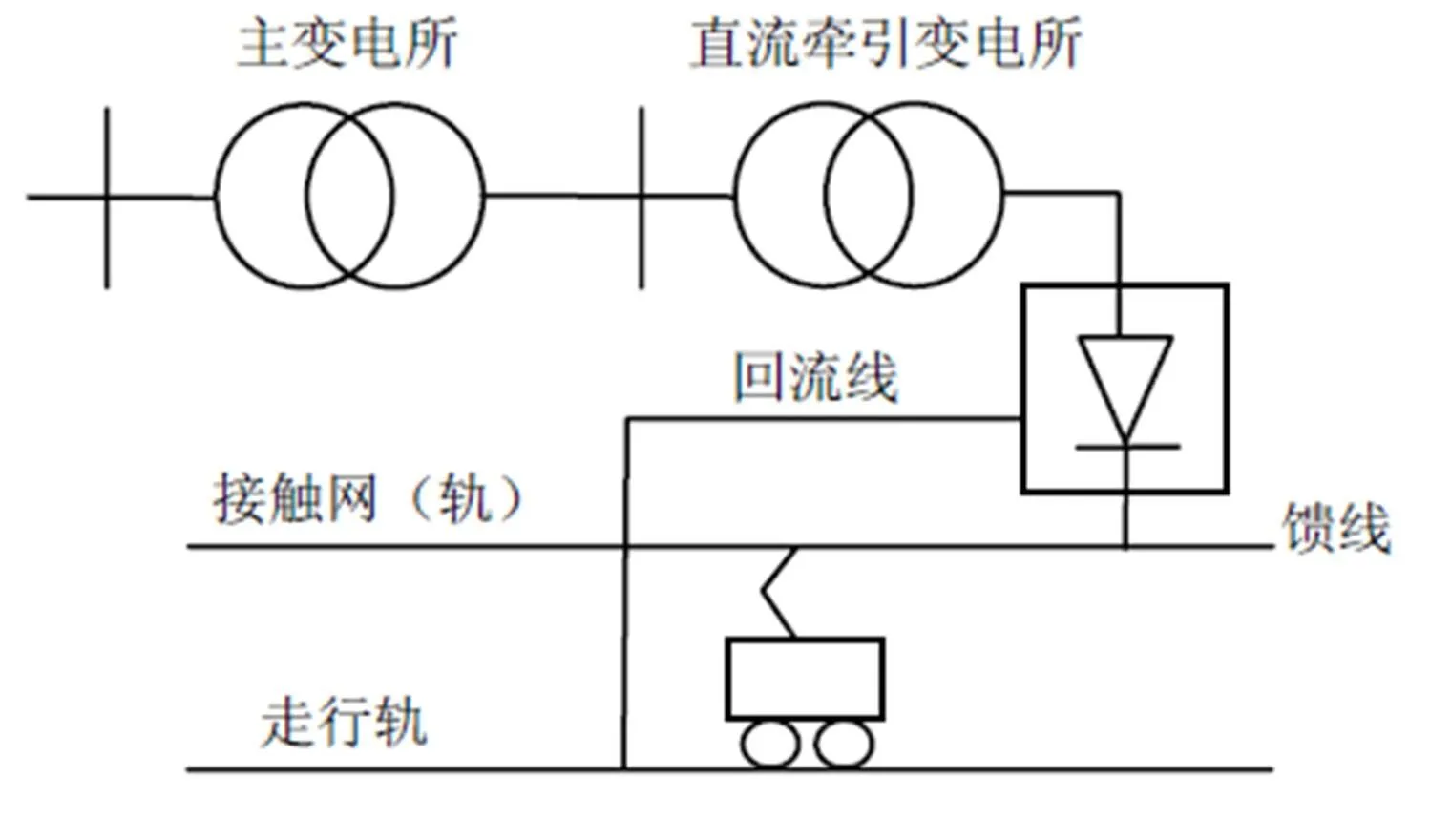
图1 直流牵引供电系统示意图

1.1 牵引变电所

牵引变电所内主要包含牵引变压器和整流器，三相交流电经牵引变压器降压、整流器整流后变换为适合电力机车牵引用的直流电。整流机组是牵引变电所的关键设备，目前我国地铁普遍采用2套12脉波整流机组分别移相+7.5°和-7.5°后并联形成阀侧电压相位相差15°的24脉波整流电路。牵引变电所设置的数量、位置及容量需满足远期高峰小时负荷的供电要求。

1.2 牵引网

牵引网由馈线、接触网、钢轨和回流线组成。其中接触网按结构不同可以分为架空式接触网和接触轨，架空接触网根据悬挂形式的不同可以分为柔性悬挂接触网和刚性悬挂接触网；接触轨和走行轨平行布置，所以接触轨又被称为第三轨[10，11]。

2 直流牵引供电系统的数学模型

2.1 整流机组的外特性模型

在地铁直流供电系统短路分析中，整流机组的外特性曲线对短路分析至关重要。对整流机组的外特性曲线进行分段线性化处理，可以满足实际工程设计中对精度的要求。

24脉波整流机组的外特性曲线十分复杂，在工程计算中，可以认为组成24脉波整流机组的2个12脉波整流电路并联独立工作。12脉波整流机组采用轴向双分裂式三绕组变压器，其等效电路如图2所示。

图2 轴向双分裂式变压器等效电路

假设2=3，则穿越阻抗k（副边2个绕组并联短接，原边绕组接电源时的短路阻抗）和半穿越阻抗b（2个副边绕组之一开路，另一个绕组短路，原边绕组接电源时的短路阻抗）分别为k=1+2/ 2，b=1+2。考虑系统电抗s后，分裂变压器的耦合系数= (s+1) / (s+1+2)。

12脉波整流电路直流电压输出调整特性可分为6种不同的状态[12]。

d1=d0-cd（1）

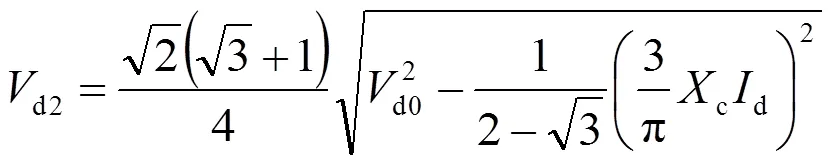
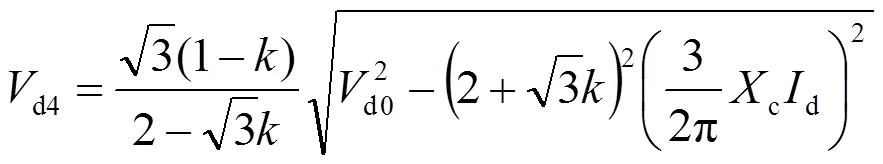
基于整流变压器负载能力的要求，上述6个工作区间相邻区间的临界电流如表1所示。

表1 临界电流求解式

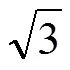
整流机组工作在d1、d3、d5-1和d5-2状态时，外特性曲线为直线形；工作在d2和d4状态时，外特性曲线为曲线形。在工程应用中，可将外特性曲线用连接其起点和终点的直线代替。各直流电压输出调整特性表达式的斜率即为电压源内阻，截距即为等效理想电压源数值。

2.2 牵引变电所的等效模型

在戴维南等效电路中，牵引变电所模型用等效内电阻eq与理想电压源eq相串联表示，在诺顿等效电路中，牵引变电所模型用等效内电阻eq与理想电流源相并联表示。理想电压源由交流电源空载电压、系统阻抗和整流机组的有关参数及其工作状态决定。等效内电阻由交流电源的系统阻抗、整流元件的电压降、整流变压器的阻抗以及整流电路的工作状态决定。

在实际计算中，可以利用整流机组的外特性曲线得到牵引变电所的等效电阻eq和理想电压源eq。整流机组的外特性曲线的斜率为等效电阻eq，与轴的截距为理想电压源eq。牵引变电所的等效模型如图3所示。

图3 牵引变电所等效模型

2.3 牵引网的数学模型

牵引网由接触网和回流网2部分组成。接触网作为牵引网的正极，列车通过接触网取电；回流网作为牵引网的负极，是列车电流的回流装置。回流网通常由钢轨代替，也有少量地铁使用铺设在钢轨旁的单独回流线。

由于钢轨与接触网通常采用与地绝缘方式安装，可忽略大地对牵引网阻抗的影响。同时由于馈线距离相对接触网的距离非常短，馈线电阻可忽略不计，所以在直流稳态短路电流的计算中，只需考虑接触网（轨）及走行轨的电阻。

走行轨电阻率为2.1×10-7W·m，接触轨的电阻率为1.25×10-7W·m。各种型号走行轨和接触轨的基本参数如表2所示。

表2 走行轨和接触轨基本参数

其中，为每米钢轨的质量；为钢轨的横截面积；为横截面周长；1为与钢轨横截面面积相同的圆半径，2为与钢轨横截面周长相同的圆半径，即

钢轨（包括走行轨和接触轨）的直流电阻可以根据其材料电阻率和横截面积求得，即

R

d

=

r

/

S

×10

7

(

W

/km)。

其中，为电阻率，W·m；为钢轨横截面积，cm2。

1 m长钢轨的质量为= 0.783(kg)，因此钢轨直流电阻的求解式可以表示为

对于单根走行轨，其单位长度直流电阻为

该直流电阻是单根走行轨的单位电阻，对于上下行并联系统，4根走行轨并联，则其直流电阻为d走行轨/ 4(W/km)。

实际中考虑到线路上钢轨的磨损、钢轨接头、信号轨道电路扼流变压器及连接电缆的影响，实际单根走行轨的直流电阻值还要大一些。

对于单根接触轨，其单位长度直流电阻为

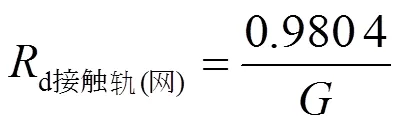
该直流电阻是单根接触轨的单位电阻，对于上下行并联系统，2根接触轨并联，则其直流电阻为d接触轨(网)/ 2（W/km）。

3 直流短路稳态计算模型

3.1 直流侧牵引网单边供电短路稳态模型

牵引网单边供电短路故障时的等效电路如图4所示。

图4 单边供电短路等效模型

短路点距离牵引变电所的距离为d，J为接触轨（网）电阻，Z为走行轨电阻，对于上下行并联牵引供电系统，上下行接触网（轨）并联（2根），上下行走行轨并联（4根），则有J=d接触轨(网)·d/ 2，Z=d走行轨·d/ 4。图4中的1、3、5为接触网电阻（上下行并联），2、4、6为走行轨电阻（上下行并联），1、I2、3为流经馈线开关的短路电流，eq1、eq2、eq3为各牵引变电所供出的短路电流，d为流经短路点的短路电流，eq1、eq2、eq3为各牵引变电所的等效电压，eq1、eq2、eq3为牵引变电所的等效电阻。

1座牵引变电所单边供电时，短路电流为

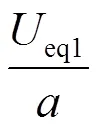
2座牵引变电所单边供电时，

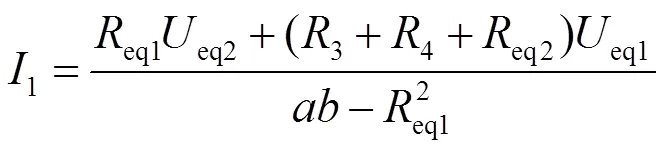
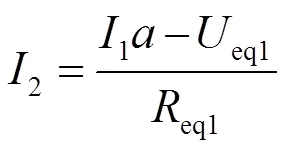
eq1=1-2

eq2=2

d=1

3座牵引变电所单边供电时，

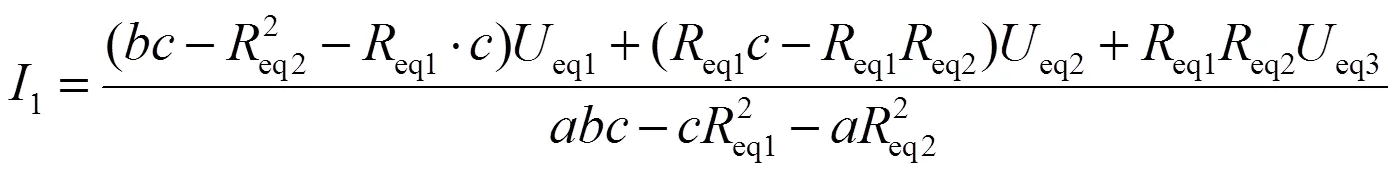
eq1=1-2

eq2=2-3

eq3=3

d=1（12）

式中，=1+2+eq1，=3+4+eq1+eq2，=5+6+eq2+eq3。

3.2 直流侧牵引网双边供电短路稳态模型

采用双边供电的牵引供电系统中某一点发生短路时，不仅短路点处的牵引变电所向短路点供电，而且全线所有牵引变电所都向短路点供电。为简化计算，只考虑2个牵引变电所供电，接触网（轨）发生短路的牵引网双边供电短路稳态等效电路如图5所示。

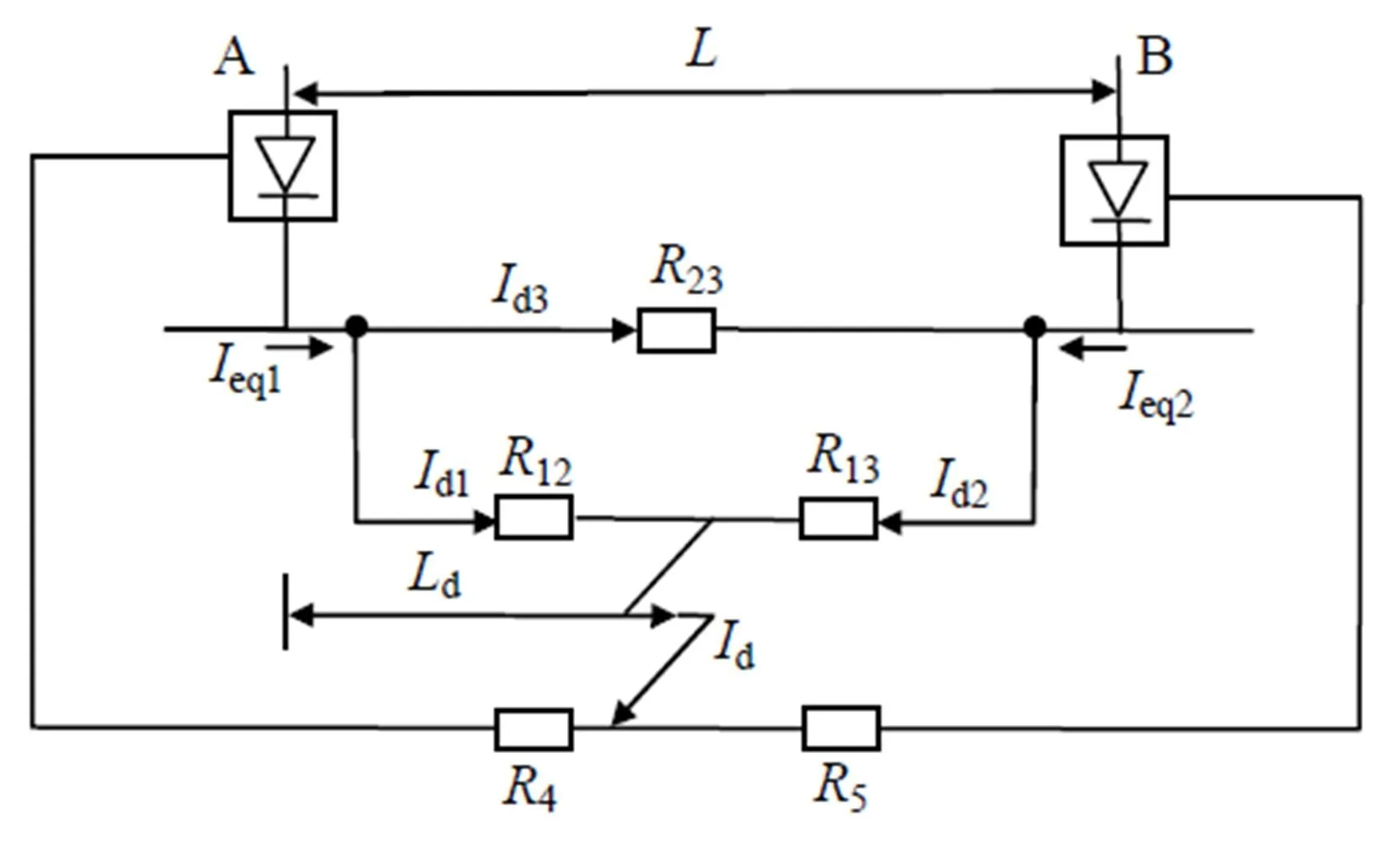
图5 双边供电短路等效模型1

2座牵引变电所正常双边供电时，2座牵引变电所之间的间距为，短路点距离变电所A的距离为d，12、13、23为接触网（轨）电阻，4、5为走行轨电阻，则有

12=d接触轨(网)×d（13）

13=d接触轨(网)×(-d) （14）

23=d接触轨(网)×（15）

将图5的模型进行变换即可得到双边供电牵引网短路简化示意图，如图6所示。

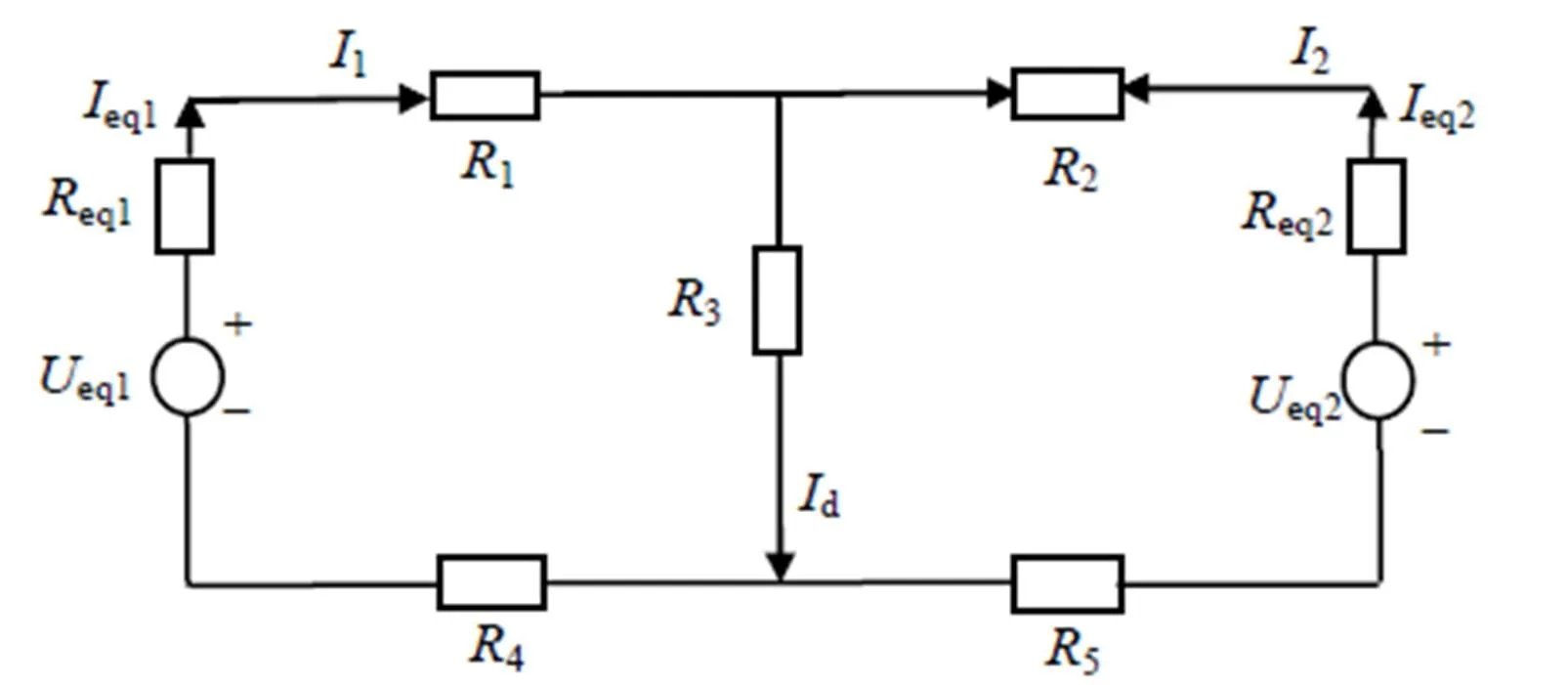
图6 双边供电短路等效模型2

此时，短路电流计算式为

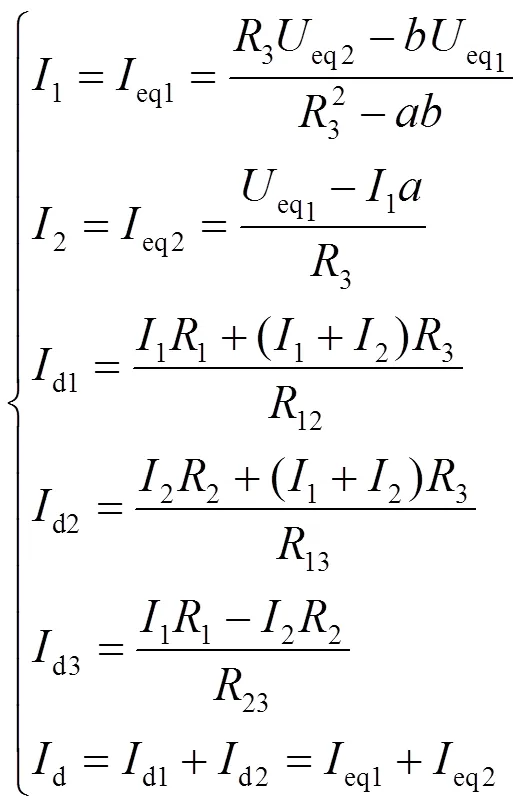
式中，=1+3+4+eq1，

=2+3+5+eq2。

如果得到的d3为负数，则说明假设的电流方向和实际电流方向相反。

考虑相邻牵引变电所影响正常双边供电短路等效模型如图7所示。

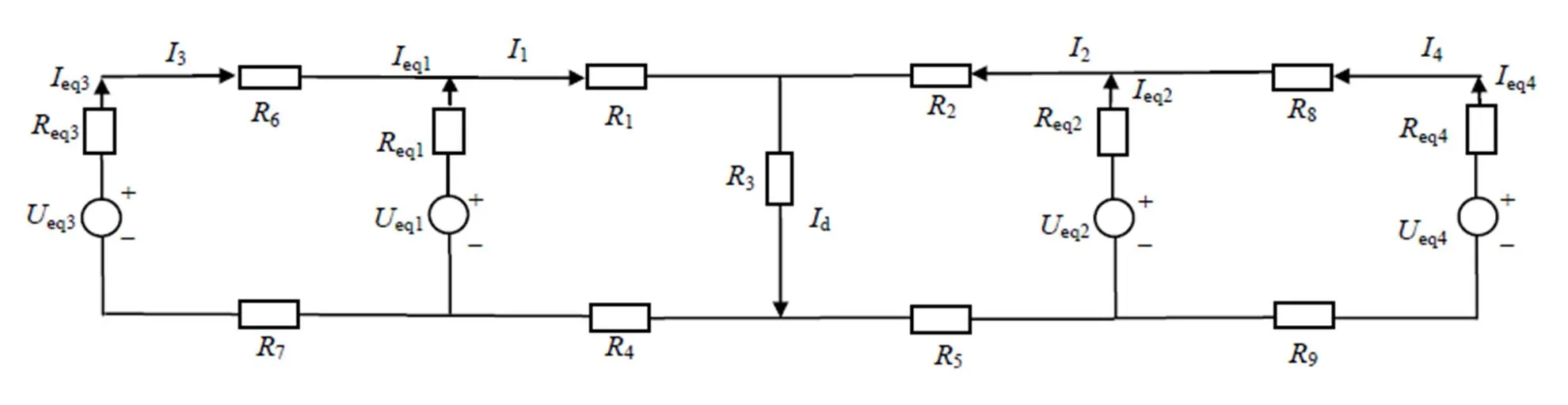
图7 考虑相邻两侧牵引变电所影响正常双边供电短路等效模型

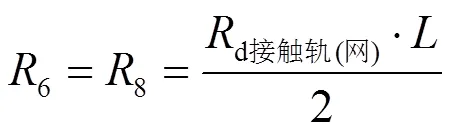
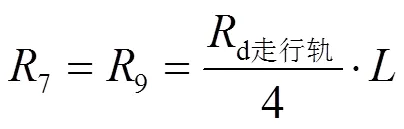
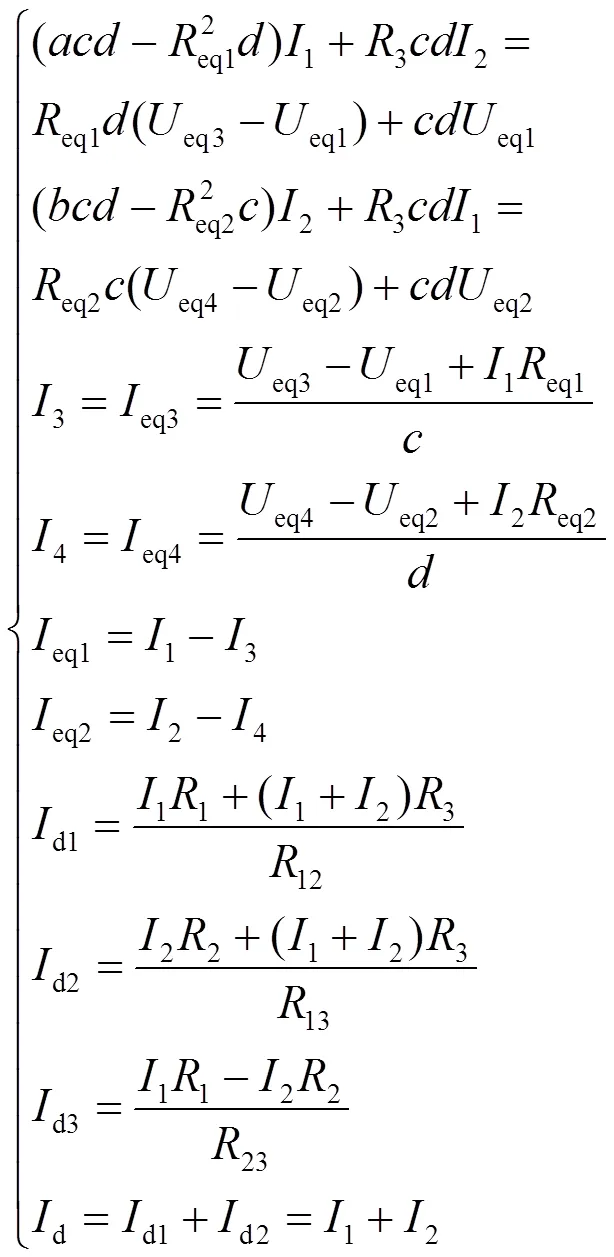
式中，=1+3+4+eq1，=2+3+5+eq2，=6+7+eq1+eq3，=8+9+eq2+eq4。

4 计算实例

4.1 案例条件

电网部分：交流侧电压1N= 35 kV；交流侧短路容量kA=kB= 100 MV·A；分裂变压器穿越阻抗为0.037 13W，半穿越阻抗为0.060 34W。

整流机组部分：机组容量nA=nB= 3 000 kV·A；阀侧电压2N= 1 180 V。

牵引网部分：两牵引变电所距离= 3 km；走行轨电阻p= 0.013W/km（4根的并联值）；接触网电阻o= 0.021 3W/km（单根接触线的值）。

求距A牵引变电所1 km处短路时接触网的短路稳态电流值。

4.2 稳态短路电流计算

已知穿越阻抗和半穿越阻抗，则换相电抗为

cA=cB=bA+sA= 0.074 264W

耦合系数为

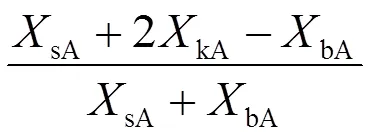
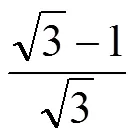
根据表1可以求出临界电流，如表3所示。

下面分别求解6个工作状态下的等效电源和等效电阻值，因为第1、3、5、6个状态的外特性曲线为直线，可以直接求解，第2、4个状态的外特性曲线为曲线，通过与相邻2个状态的交点进行求解，根据式（1）—式（6）可以得到各工作状态的等效电源、等效电阻值及负荷电流范围。

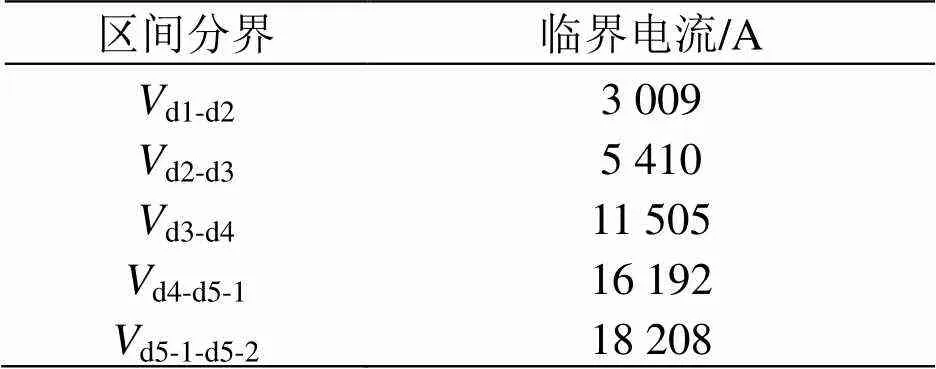
表3 临界电流

牵引整流机组各状态等效计算结果见表4。

表4 牵引整流机组各状态等效计算结果

根据计算条件对图6中的电阻1、2、3、4和5进行求解，并根据式（18）对各牵引变电所供给的短路电流进行计算，结果如表5所示。

1=od/ 2 = 0.005 325W（22）

2=o(-d) / 2 = 0.037 275W（23）

3=od(-d) / 2= 0.004 659W（24）

4=pd= 0.006 5W（25）

5=p(-d) = 0.045 5W（26）

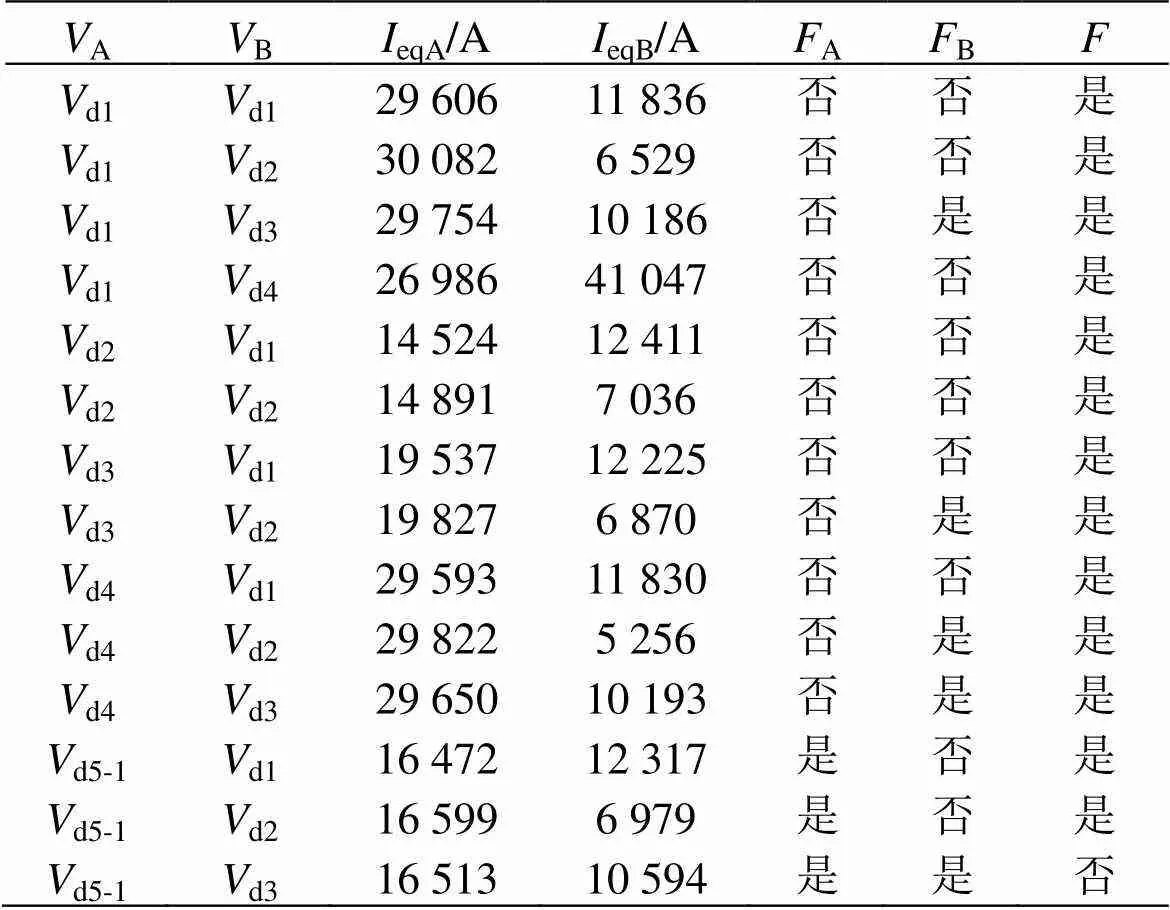
表5 短路稳态电流计算结果

表5中，A、B分别表示变电所A、变电所B的工作状态；A（B）为“是”表示牵引变电所A（B）供给的短路电流在负荷电流范围内，为“否”表示牵引变电所A（B）供给的短路电流不在负荷电流范围内；为“是”表示A或B供给的短路电流不在负荷电流范围内，为“否”表示A和B供给的短路电流都在负荷电流范围内。所以eqA= 16 513 A，eqB= 10 594 A，d1= 20 115 A，d2= 6 991 A，d3= -3 603 A，d= 27 106 A。

由此可得，牵引变电所A提供的短路电流为16 513 A，牵引变电所B提供的短路电流为10 594 A，总的短路电流为27 107 A。

当考虑变压器A、B两侧相邻牵引变压器的影响时，对正常双边供电情况下的短路电流进行计算，4个牵引变电所的参数相同。根据计算条件对图7中的电阻进行求解，其中电阻1、2、3、4和5根据式（22）—式（26）进行求解，6、7、8、9的求解式为

6=8=o/2 = 0.042 6W（27）

7=9=p= 0.052W（28）

当A、B、C、D变电所的工作状态均为d1时，11= 0.047 744W，22= 0.118 694W，33= 0.157 12W，44= 0.157 12W，通过式（21）得到1= 36 945 A，2= 12 634 A，3= 7 350 A，4= 2 514 A。各牵引变电所供给的短路电流为：eqA= 29 595 A，eqB= 10 121 A，eqC= 7 350 A，eqD= 2 514 A。短路电流d= 49 580 A。判断eqA、eqB、eqC、eqD是否均在各自要求的负荷电流范围内，只要其中之一不满足要求则需重新选取A、B、C、D变电所的工作状态，直至eqA、eqB、eqC、eqD均在各自要求的负荷电流范围内，此时的短路电流及各变电所供出电流即为所求。

具体计算流程为：（1）梳理计算条件；（2）计算理想空载直流电压、换相电抗、耦合系数；（3）根据耦合系数判断整流机组将出现的几个工作状态；（4）对出现的各工作状态根据表1对临界电流进行求解；（5）根据整流机组的外特性曲线，由式（1）—式（6）对每个状态的等效电压值和等效电阻值进行求解；（6）根据式（13）—式（17）及式（19）—式（20）对稳态短路电流进行计算；（7）对等效电路中的牵引网参数进行求解；（8）假设各牵引变电所的工作状态均为d1，由式（21）对短路电流进行求解；（9）判断各所供给的短路电流是否在负荷范围内，只要其中一个牵引变电所不满足要求则重新假设各牵引变电所的工作状态；（10）循环步骤（8）和（9），直至各牵引变电所供给的短路电流均在负荷范围内。

5 结语

本文基于建立的整流机组、牵引变电所、牵引网的数学模型，进行单边供电短路计算和双边供电短路情况下线路等效模型的简化，并推导各种计算情况下每个变电所供给短路电流和总短路电流的计算式。通过实例分析利用电路图法计算短路稳态电流的具体过程，为直流设备选型、继电保护整定及地铁电动车辆主保护电器选择等提供依据。

[1] 黄德胜，张巍. 地下铁道供电[M].北京：中国电力出版社，2009.

[2] Paolo Pozzobon. Transient and Steady-State Short-Circuit Currents in Rectifiers for DC Traction Supply[J]. IEEE Transaction on Vehicular Technology, No.4,1998.

[3] 何宗华. 城市轻轨交通工程设计指南[M]. 北京：中国建筑工业出版社，1993.

[4] 刘炜，李群湛. 基于多折线外特性模型的直流牵引供电系统稳态短路计算[J]. 机车电传动，2008（1）：61-65.

[5] J.C. Brown, PhD. Calculation and Measurement of Rail Impedances Applicable to Remote Short-Circuit Fault Currents. IEE PROCEEDINGS-B, JULY 1992: Vol. 139, No.4.

[6] 龚延志. 直流牵引供电系统数学模型与短路计算研究[D]. 北京交通大学，2009.

[7] 张峻领. 地铁供电系统直流侧短路故障研究[D]. 西南交通大学，2011.

[8] 曹建设，杲秀芳. 直流牵引网短路电流的计算[J]. 城市轨道交通研究，2008（2）：31-34.

[9] 乌正康，杨其华. 地铁牵引供电网短路稳态仿真分析[J]. 铁道学报，1993（1）：39-44.

[10] 李良威. 城市轨道交通直流侧短路故障研究[D]. 西南交通大学，2007.

[11] 刘炜，李群湛，陈民武. 城市轨道交通交直流统一的牵引供电计算[J]. 电力系统保护与控制，2010，38（8）：128-133.

[12] 黄维军. 城市轨道交通DC1500V牵引供电系统短路故障分析[D]. 西南交通大学，2010.

The various parameters of DC short circuit of unilateral and bilateral power supply have been calculated, and expression formulae for short circuit current and short circuit current at all short circuit points in short circuit steady state model for DC traction network unilateral power supply and bilateral power supply are derived respectively on the basis of the external characteristics model of rectifier set and mathematical models of traction substation and traction network, by application of circuit diagram method to solve various parameters of DC short circuit for unilateral and bilateral power supply, and the steady state short circuit current of DC traction network has been calculated by means of analyzing of living examples.

Urban mass transit; circuit diagram method; steady state short circuit; unilateral power supply; bilateral power supply

10.19587/j.cnki.1007-936x.2018.05.015

U231.8

B

1007-936X(2018)05-0055-06

2018-01-28

李丹丹.北京城建设计发展集团股份有限公司轨道院，硕士研究生。研究方向为牵引供电系统电能质量、谐波谐振与抑制技术、城市轨道交通等。