基于加权等值法的含小水电群电网小干扰稳定性分析
2018-11-06,,,,
,,,,
(国网咸宁供电公司,湖北 咸宁 437000)
1 引言
对于富含小水电群的地区,由于小水电机组容量小,机组数目多,接入方式多样,其并网后容易引发一系列稳定性方面的问题。大量小水电的并网且大部分机组采用快速励磁,在某些特殊运行方式下,容易诱发低频振荡现象的发生。最早的互联系统联络线上的低频振荡现象是1964年美国西部的西北联合系统与西南联合系统以230kV线路互联时观察到的,联络线上持续的0.1Hz的低频振荡常常导致联络线解列。我国在八十年代初在进行滇南、滇中联网,华北、华中联网试验时也曾发现联络线上的低频振荡现象[2]。
本文对小水电群并网后的电力系统进行小干扰稳定性分析,由此来找出系统可能存在的弱阻尼模式,从而采取相关措施来抑制可能发生的低频振荡现象。而由于小水电数目多,系统结构复杂,故需要对富含小水电群的电力系统进行等值,在进行等值前,首先需要对系统的机组进行同调机群的判别,利用电气距离法将经同一变电站上网的小水电机组近似划分为一个同调机群。其次,对同调机群进行等值,国内现有的动态等值程序应用最广泛的是频域聚合,而频域聚合法过程复杂,等值时间长,因此本文提出基于加权平均思想的参数聚合[3],此方法不仅保证了等值的精度,而且简化了参数聚合的程序,从而大大提高计算速度,有利于工程的实现。
2 加权等值法
加权等值法的基本思想是以同调机群中各发电机额定容量与等值机额定容量的比值对发电机各参数予以加权。在进行加权等值前,要对系统进行同调进群的判别,本文的同调机群是通过电气距离法判别得来,电气距离De是系统中两机组的距离,也可以体现两机组的关联程度。对于两台发电机来说,当其电气距离小于某一阈值Dε时,可将其划分为同调机组;而对于多机系统来说,则先将其进行系统聚类,再根据电气距离法得到同调机群;本论文所研究的小水电群所处的网络大部分是辐射状网络,接于同一母线上的发电机间的电气距离较近,故本文可将接于同一母线上的发电机组可近似划分为一个同调机群[4]。
加权法的等值过程主要是通过发电机及调节系统、发电机电磁回路、发电机励磁系统、原动机及调速器系统环节来完成的。
2.1 发电机转子运动方程的聚合
设通过相关识别得知某个相关机群G={1,j,N},其中包括N台相关发电机。鉴于合成的等值机的容量为各台电机的容量(MVA)之和,G表示待聚合的等值机,可推导出等值发电机及其调节系统的详细模型参数。即
(1)
假设发电机j摇摆方程为:
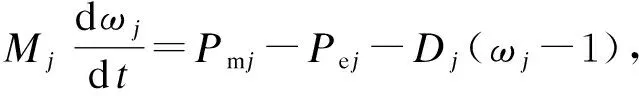
(2)
式中,Mj为发电机j的惯性时间常数,Pmj为输入机械功率,Pej为输出电磁功率,Dj为阻尼系数。各参数值均以其自身额定容量为基值的标幺值。将N台同调机运动方程进行叠加,并假设各同调机的转速相同,则得到聚合后的等值机转子运动方程为:
(3)
其中MG,PmG,PeG,DG均以式(2)~(4)进行加权等值。
(4)
2.2 发电机电磁回路的聚合
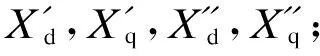
2.3 发电机励磁调节系统的聚合
以IEEE-1 型励磁调节系统说明,如图1所示。
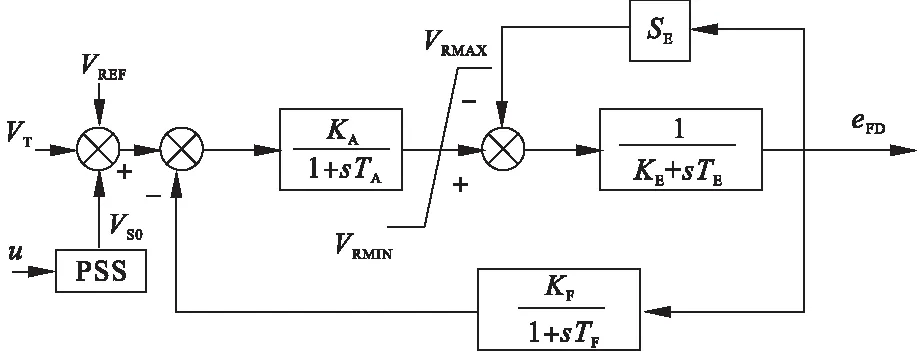
图1 励磁单元传递函数
图中,KA,TA为励磁系统放大环节的增益和时间常数,KE,TE为励磁系统励磁环节的增益和时间常数,KF,TF为励磁系统反馈环节的增益和时间常数,VRMAX,VRMIN为励磁系统的最大、最小输出;其中SE为励磁环节的饱和系数,eFD为励磁环节的输出电压。等值系统也为上图的传递函数框图,参数按照加权平均的方法即式(4)求得。
2.4 原动机及调速系统参数聚合
由于参与等值的机组均为小水电,故水轮机传递函数如图2所示。
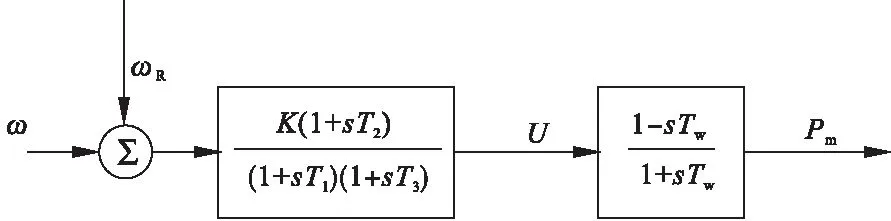
图2 调速器和原动机传递函数
(5)
K为调速系统放大倍数,T1为调速器时间常数,T2为倒阀时间常数,T3为伺服时间常数,TW为水锤效应时间常数,则等值机参数可由式(1)~(4)求得。
3 小水电群的小干扰稳定性分析
对富含小水电群的电力系统进行小干扰稳定性分析时,其特点是要对众多小水电采用加权法进行等值,本文中加权法等值是对小水电群的发电机及调节系统、发电机电磁回路、发电机励磁系统、原动机及调速器系统分别等值,最后可得到各片区的等值发电机组,形成整个系统的等值模型。
3.1 IEEE 10机39节点系统算例
对新英格兰系统IEEE 10机39节点系统进行等值,并将等值系统与原系统进行仿真比较。如图3,10机39节点系统包含10台发电机,39个节点和46条线路,选择第9号发电机G9为参考发电机,且将G9等效为外部电力系统,第5号发电机G5为研究对象。所有发电机均采用三阶模型,励磁调节器采用三阶模型,运用加权平均的聚合方法进行参数聚合。
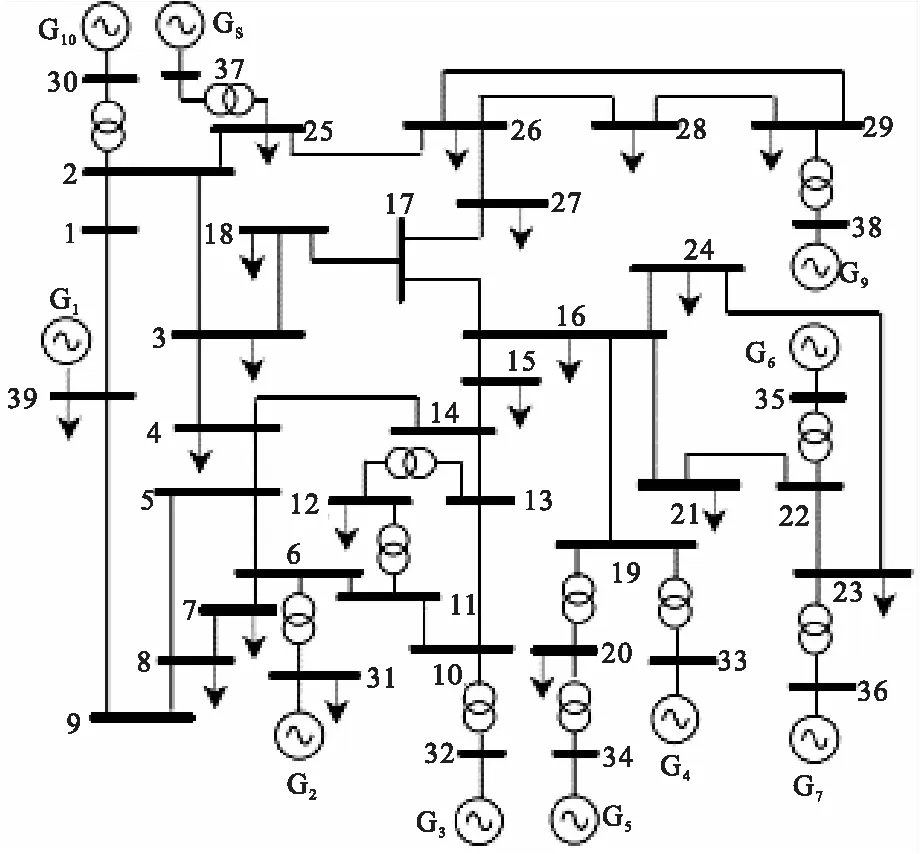
图3 10机39节点系统网络结构图
调用基于格纳姆矩阵的发电机相关识别程序进行识别[4],得到3组同调机群:机群1(G8,G10)、机群2(G2,G3)、机群3(G4,G6,G7),表1列出机群2(G2,G3)的原系统参数、加权聚合法的聚合参数为例进行比较。
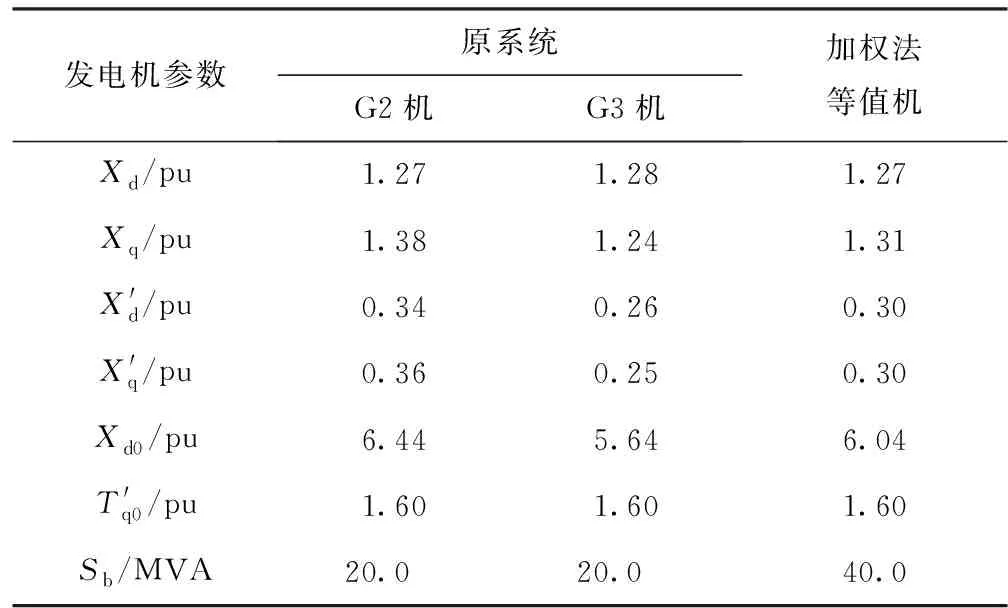
表1 机群2等值发电机参数
选取故障为:在第0.5s时,线路25~26发生三相短路故障。在第0.56s时切除故障,此时系统没有失去稳定;在第0.7s 时切除故障,此时系统失去稳定。在PSASP 环境下对原系统及加权法等值系统进行仿真对比,曲线为以G9发电机为参考机时,G5发电机的功角曲线。可以看出,等值前的发电机功角曲线与等值后发电机功角曲线几乎重合,说明加权聚合法的等值效果好,详细结果如下图。
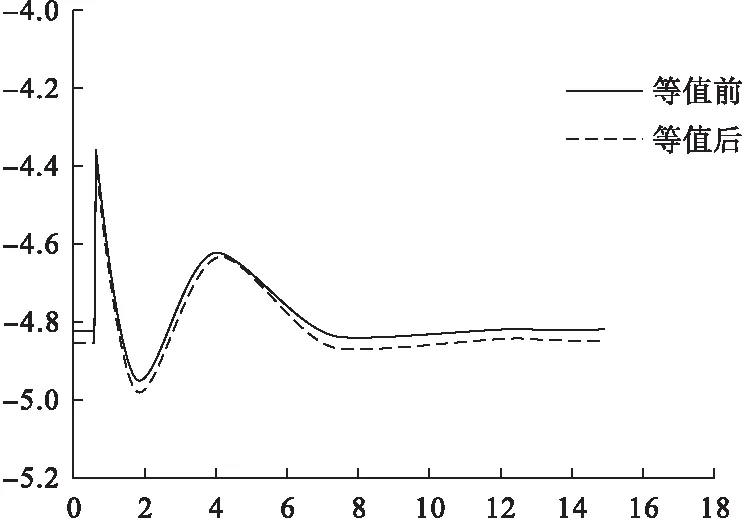
图4 G5功角曲线图(系统未失稳)
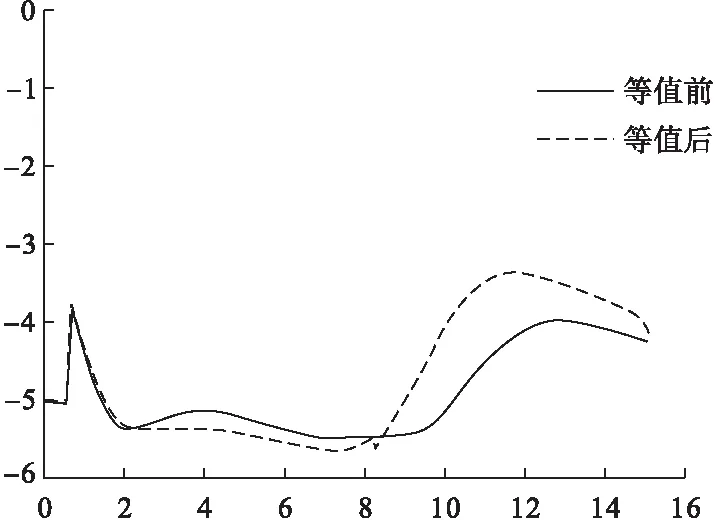
图5 G5功角曲线图(系统失稳)
3.2 A地区中Y片区电力系统算例分析
采用10机39节点算例的等值方法对研究地区的小水电进行等值,在两条不同的线路设置三相短路故障,命名为故障A和故障B,如图6所示。
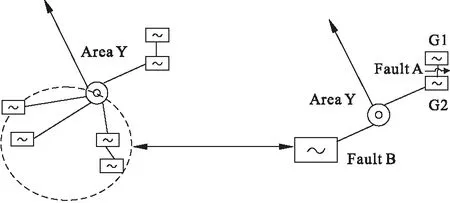
图6 三相短路故障A和三相故障B
两个故障均为在1s时线路的首端发生三相短路,在1.1s时切除此故障线路。得到发电机组G1的功角图(以发电机组G2为参考机组)。
由以上两个图可知:发生三相短路故障A时,等值前后系统的功角曲线几乎重合,发生三相短路故障B时,等值前后系统的功角曲线同样几乎重合。这说明加权聚合法的等值效果达到预期良好效果。
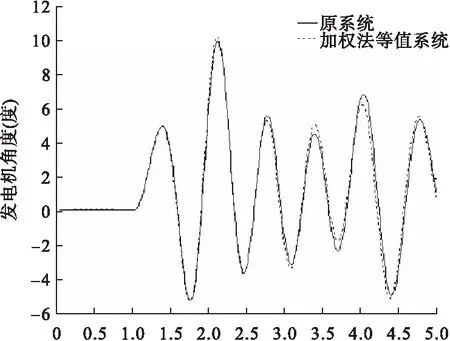
图7 G1功角曲线图(故障 A)
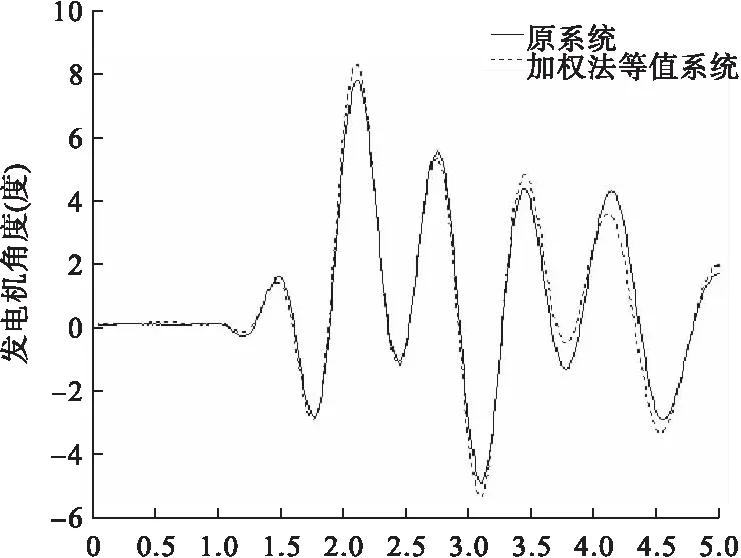
图8 G1功角曲线图(故障 B)
4 A地区小干扰稳定性分析
对小水电等值模型进行小干扰稳定性分析,可得到如下结果:(衰减阻尼比小于3%为弱阻尼。研究地区可分夏季和冬季两种方式进行计算,根据全年负荷监测及负荷预计的情况,又可以将运行方式分为大负荷运行和小负荷运行,故整体上运行方式可以分为夏大、夏小、冬大、冬小运行方式。)
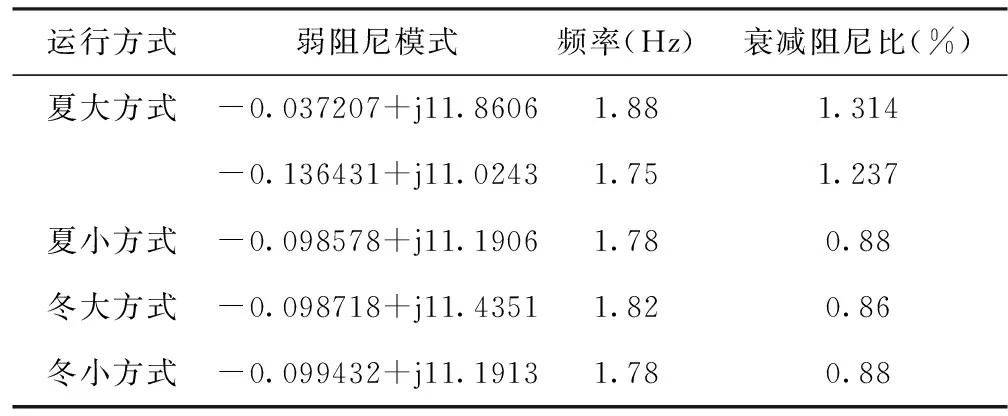
表2 研究地区小干扰稳定性分析结果
5 结论
通过对研究地区的小水电机组进行加权等值,并进行小干扰稳定性分析,可得以下结论:①利用加权等值法的仿真效果良好;②由于大量小水电的接入,使得系统的阻尼变弱,因此更容易引发低频振荡现象,严重威胁了电网的安全稳定运行。
