蒙华铁路阳城隧道土砂分界地层分界面位置对围岩稳定性影响探究

王志杰，李瑞尧，徐海岩，唐 力，徐君祥，周 平

(西南交通大学交通隧道工程教育部重点实验室,四川 成都 610031)

0 引言

蒙华铁路是我国北煤南运的国家战略运输新通道，是国家综合交通运输系统的重要组成部分。阳城隧道作为蒙华铁路关键性控制工程之一，地质条件极为复杂，穿越地层包括全风化红砂岩地层、土砂分界地层和土砂互层地层。隧道在施工阶段出现了初期支护开裂变形、掌子面坍塌和涌水涌砂等情况。

国内外学者采用理论分析、数值模拟、现场试验和室内试验等方法对软弱地层隧道围岩稳定性进行研究。关宝树[1]针对日本、美国和欧洲等国的隧道开挖方法及隧道开挖工法选择的基本条件进行了归纳，包括施工条件、围岩条件、工期和环境条件、隧道断面面积及埋深等；李国良[2]依托郑西、宝兰高铁，对大断面黄土隧道台阶法开挖的适用性进行试验研究，得到采用台阶法一定程度上可加快施工进度的结论；杨建民[3]以郑西铁路大断面黄土隧道为依托，对多种开挖工法进行分析，提出非特殊情况下高速铁路大断面黄土隧道宜采用三台阶七步法开挖；张德华等[4]以兰新铁路大梁山隧道为工程背景，采用数值模拟、现场试验等方法对三台阶七步开挖法施工的高地应力隧道支护结构受力进行研究；朱望瑜[5]结合太中银铁路土石分界地层隧道施工，通过数值模拟分析了台阶法开挖不同台阶参数对隧道稳定性的影响；杨斌等[6]以互层围岩为研究对象，将近水平软硬互层围岩等效为横观各向同性岩层，建立平面应变有限元模型对支护结构受力进行分析，得到了开挖后拱顶及仰拱向内侧弯曲的结论；李奎[7]对隧道穿越水平层状围岩的压力拱进行了研究，通过数值模拟探究了双层围岩隧道的塑性区分布；黄彬[8]针对隧道穿越黄土土石分界地层大断面隧道进行了施工技术方面的研究，得到爆破施工的技术要点等。

三台阶七步开挖法在偏压、高地应力及软岩地层等不同地层中均有研究[9]，但是在互层围岩及分界地层中的研究并不全面，尚需要补充。虽已有学者对互层围岩施工方法进行了研究，包括施工工法对围岩稳定性的影响、支护参数的设计等[10-15]，但针对分界面的影响尚未有系统研究。本文从分界面入手，通过调整土砂分界地层相对层厚，研究三台阶七步开挖法施工的土砂分界地层隧道围岩变形、塑性区扩展以及支护结构受力对围岩稳定性的影响。

1 工程概况

阳城隧道位于蒙华铁路浩勒报吉至三门峡段，地理位置处于陕西省榆林市靖边县附近，起讫里程为DK242+041～DK249+134，全长7 093 m，最大埋深约207 m，设计时速120 km。阳城隧道为单洞双线隧道，开挖断面在100 m2以上，属大断面隧道。

隧道地层岩性主要为第四系上更新统风积(Q3eol)砂质新黄土及黏质新黄土、第四系中更新统冲洪积(Q2al+pl)中砂、白垩系下统洛河组(K1l)砂岩。其中，土砂分界地层下部为全风化砂，上部为砂质新黄土局部夹块石，掌子面素描图及现场图如图1所示。

(a) 掌子面素描图1 (b) 掌子面现场图1 (c) 掌子面素描图2 (d) 掌子面现场图2

图1掌子面素描图及现场图
Fig.1 Sketches of tunnel face and site photos

2 初期支护开裂变形

2017年10月15日01：00时，阳城隧道大里程段在台阶平整过程中发现中台阶左侧拱脚处局部发生涌水涌砂。为保证施工安全，立即对初期支护进行支撑加固，约04：00，DK245+270左侧边墙位置处初期支护开裂，并有发展趋势，后期对变形段进行反压回填、压密注浆和逐榀换拱等措施，变形得以控制。变形段为土砂分界地层，右侧为强风化砂岩夹块石、左侧为土层夹砂层，围岩由Ⅴ级调整为Ⅵ级，采用三台阶七步开挖法进行施工，开挖过程中边墙及掌子面无法自稳，发生涌水涌砂现象，且掌子面发生溜塌及核心土后移；初期支护沉降及收敛较大，控制难度大。涌水、涌砂及围岩变形相关图片如图2所示。

(a) 涌水涌砂 (b) 溜塌 (c) 初期支护开裂变形

图2涌水、涌砂及围岩变形相关图片
Fig.2 Photos of water gushing,sand gushing and surrounding rock deformation

通过分析土砂分界地层围岩变形机制，除了地层围岩强度分布不均、砂岩遇水易崩解坍塌等造成大变形的主观因素，对土砂分界地层围岩的认识不足也使得隧道在设计施工中出现问题。基于此，本文采用现场试验、室内试验及数值试验等研究方式对土砂分界地层围岩稳定性进行探究，重点探讨地层种类及其厚度变化对围岩变形、围岩塑性区及支护结构受力的影响。

3 室内基本物理性能试验

本次研究的土砂分界地层为上土下砂地层，砂层为全风化砂岩夹块石，土层为砂质新黄土夹薄砂层。对天然黄土及全风化砂岩进行风干并测定含水率，进行筛分试验及颗粒密度试验；同时选取原状黄土和全风化砂岩进行固结试验、直剪试验和三轴试验，测得其压缩模量、黏聚力及内摩擦角。土砂分界地层基本物理力学试验如图3所示，基本物理参数如表1所示。

(a) 黄土风干 (b) 筛分试验 (c) 颗粒密度试验 (d) 三轴试验 (e) 固结试验 (f) 直剪试验

图3土砂分界地层基本物理力学试验
Fig.3 Basic physic-mechanical test for soil-sand strata

表1 土砂分界地层基本物理参数Table 1 Basic physic-mechanical parameters of soil-sand strata

4 数值试验

4.1 建立模型

将隧道穿越的围岩称为主层围岩，隧道拱顶至地表之间的围岩称为上覆地层，隧道仰拱拱底以下的围岩称为下伏地层，如图4所示。本次计算将土砂分界地层简化成上部为砂质黄土、下部为全风化红砂岩的分界地层。假定水平土砂分界地层土层与砂层黏结牢固且不产生滑移，即土层间的变形满足连续性。

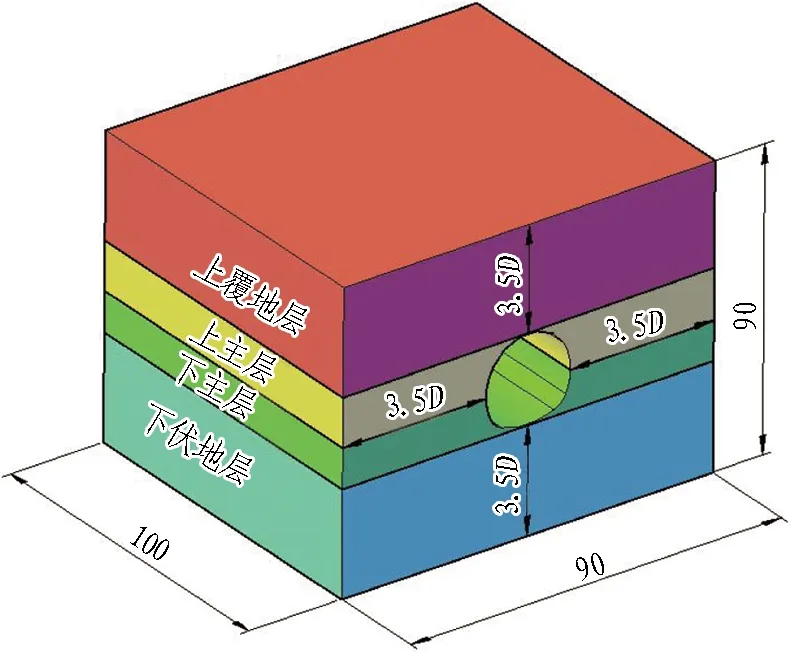
图4 计算模型示意(单位：m)Fig.4 Calculation model (unit: m)

采用有限差分软件FLAC3D进行数值模拟，土层采用弹塑性有限元模型，应用Mohr-Coulomb屈服准则，支护结构采用Elastic模型。模型尺寸如图4所示，计算参数见表2。为充分模拟现场初期的施工情况，隧道开挖方法采用与现场一致的三台阶七步法，开挖后立即支护，施工工序及参数见图5。

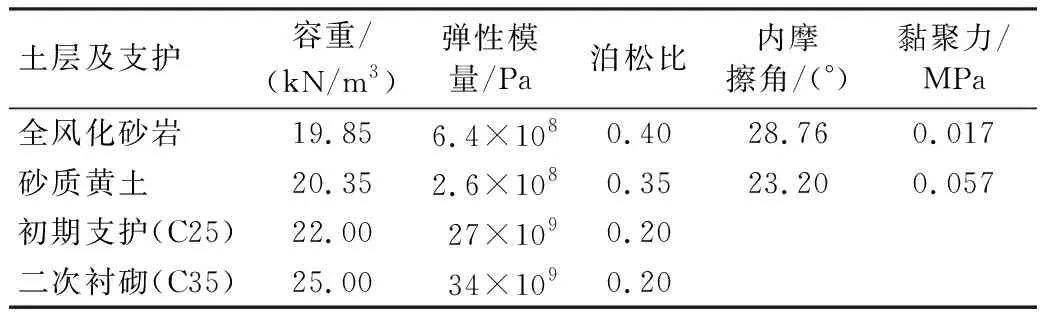
表2 计算参数Table 2 Calculation parameters

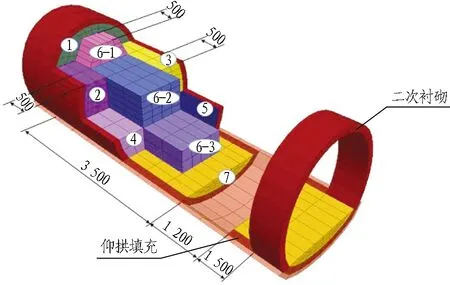
图5 隧道三台阶七步开挖法示意(单位：cm)Fig.5 Sketch of three-bench seven-step excavation method for tunnel (unit: cm)

4.1.1 不同组合地质条件下的受力和变形

主要以水平双主层地层为对象进行详细分析，地层分类及其示意图分别见表3和图6。

表3 土砂分界地层类别Table 3 Classification of soil-sand strata

注：括号内比例为主层占掌子面厚度的百分比，如1∶3模型为掌子面处25%黄土+75%红砂岩。

(a) 1∶0/0∶1模型 (b) 1∶3模型 (c) 1∶1模型 (d) 3∶1模型

图6土砂分界地层类别示意
Fig.6 Sketches of classification of soil-sand strata

隧道贯通后断面主应力分布如图7所示。由图可知，隧道贯通后不同地层分类下主应力分布范围有着很大的区别，由于三台阶七步法开挖的左右侧存在时间上的差异性，模型中左侧为先开挖部分，应力集中区域均在左侧位置，同时可以明显看出分界地层应力集中区域较大，且1∶3模型和3∶1模型产生了明显的“下垂”型的分布情况。

(a) 1∶1模型 (b) 3∶1模型

(c) 1∶3模型 (d) 1∶0/0∶1模型

图7隧道贯通后某断面应力云图
Fig.7 Stress nephograms of a section after tunnel breakthrough

4.1.2 测点布置

围岩监测点主要包含拱顶、拱肩、拱腰、拱底、各分层面与各台阶底部；初期支护应力监测点包含拱顶、拱腰、拱底、各台阶处和各分层面。监测点布置如图8所示。

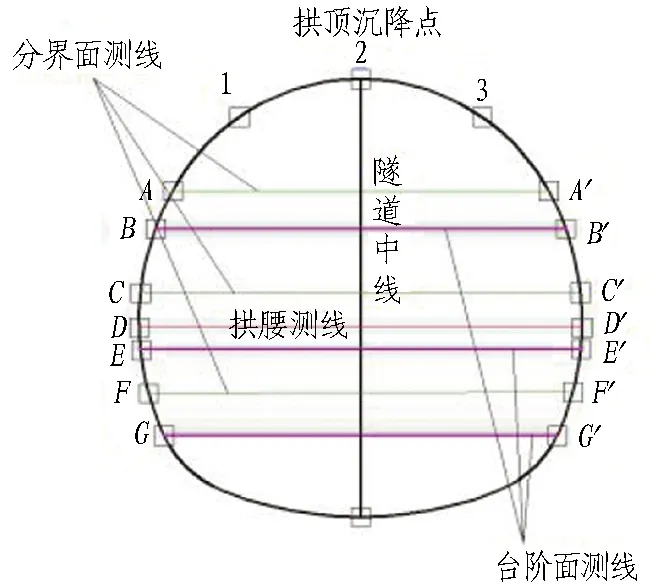
(a)围岩变形监测点

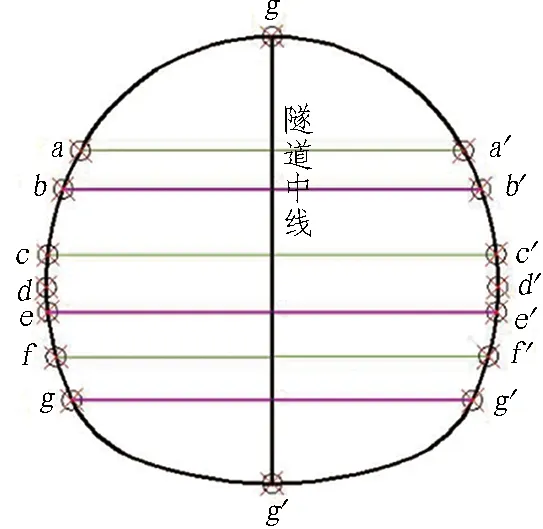
(b)初期支护应力监测点

4.2 1∶0-1∶1-0∶1模型围岩稳定性探究

如图8所示，对围岩变形及初期支护应力进行监测，以探究围岩的稳定性。首先对1∶0、0∶1及1∶1模型进行分析，对比砂质新黄土、全风化砂岩及二者1∶1土砂分界地层围岩稳定性，以探究不同类型地层围岩稳定性差异。

4.2.1 围岩变形分析

1∶0-1∶1-0∶1模型土砂分界围岩变形时程曲线如图9所示。由图可知：1)上台阶弧形导坑开挖后，监测断面收敛增长迅速，随着进一步开挖，拱顶沉降发展，上台阶初期支护完成后变形减缓，仰拱封闭后，净空收敛基本达到稳定。 2)对比3个模型的围岩变形，洞周收敛和拱顶沉降：0∶1模型>1∶1模型>1∶0模型。 3)随着隧道的开挖，3种模型沉降趋于稳定的时间并不一致，明显观察到由于土层改变而产生“稳定滞后”，这一现象主要表现在拱顶沉降上，洞周收敛则没有明显的滞后情况，1∶0模型在核心土开挖前已趋于稳定，0∶1模型在仰拱封闭成环后趋于稳定，而1∶1模型正好处于上述2个模型中间、在核心土开挖完成后趋于稳定。

(a)拱顶沉降时程曲线

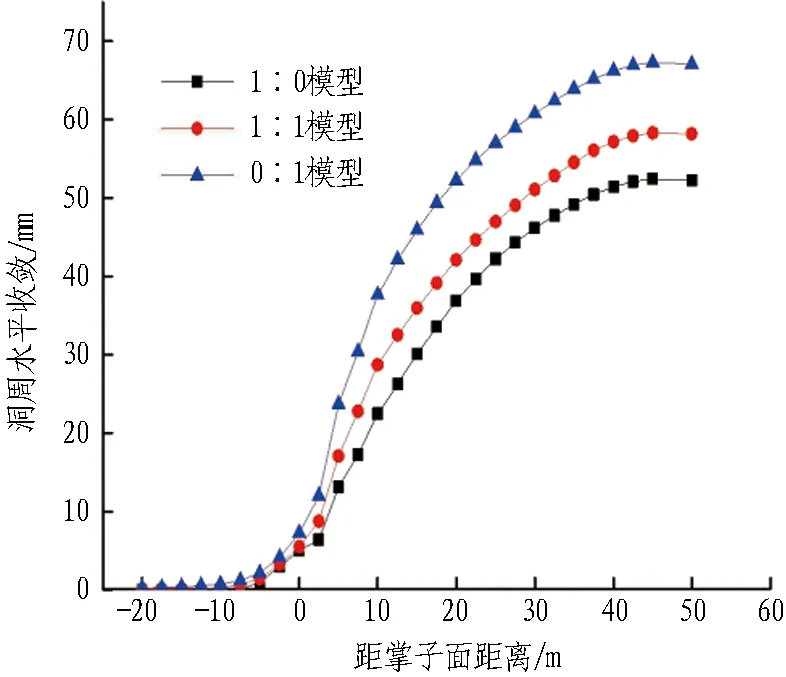
(b)拱腰收敛时程曲线

本研究中土的黏聚力优于砂，但其弹性模量和内摩擦角均劣于砂。土的变形主要由较小的弹性模量来影响，而砂由于黏聚力较小，造成的塑性流动对收敛值造成了较大的影响。综合考虑，在变形性质方面，砂是劣于土的。围岩各台阶变形时程曲线及40 m断面处围岩变形最终收敛值分别见图10和表4。

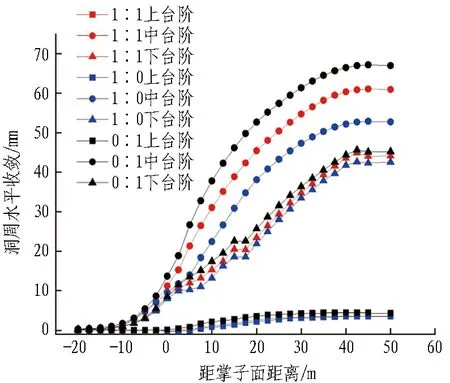
图10 1∶0-1∶1-0∶1模型土砂分界围岩各台阶变形时程曲线Fig.10 Time-history curves of bench deformation of surrounding rock in 1∶0-1∶1-0∶1 model of soil-sand strata

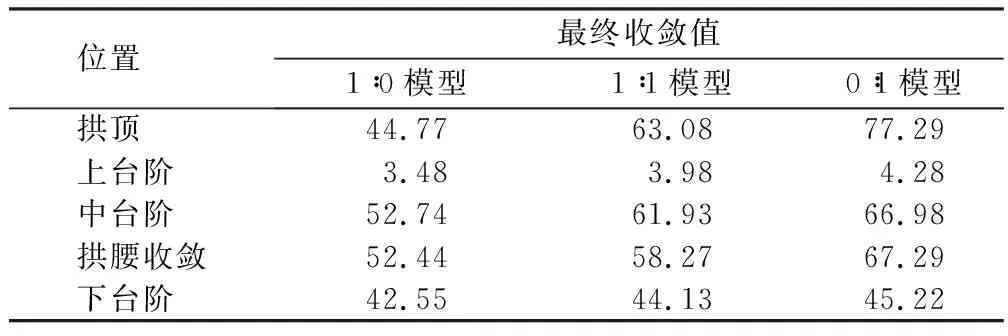
表4 1∶0-1∶1-0∶1模型40 m断面处围岩变形最终收敛值Table 4 Final convergences of surrounding rock deformation at 40 m cross-section in 1∶0-1∶1-0∶1 model mm

由图10可得：1)上、中、下3个台阶处，上台阶的收敛最小，下台阶次之，中台阶最大；2)上、中、下台阶处的收敛，1∶0模型小于0∶1模型，在变形性质方面，全土地层优于全砂地层；3)1∶1模型，各个台阶处的收敛值均处于全土和全砂之间，相比于全土地层，各收敛值更接近全砂地层。

全土地层水平收敛大于拱顶沉降，应着重对边墙处进行加固；其他地层除拱顶处需要监测并加固外，在拱腰处也应进行加固处理。

表5所示为施工各阶段变形占总变形量的百分比。由表可以得到，上、中台阶的开挖对拱顶沉降影响较大，中、下台阶、核心土开挖对水平收敛影响较大。

表5 1∶0-1∶1-0∶1模型各施工阶段变形占总变形量的百分比Table 5 Proportions of deformation of every construction phases in 1∶0-1∶1-0∶1 model in total deformation

4.2.2 围岩塑性区分析

表6所示为三台阶七步法各工序下隧道围岩塑性区变化。由表可知：1)1∶0模型(全土地层)，上台阶开挖后，掌子面范围内边墙位置出现剪切塑性区；随着中台阶左侧土体开挖(见表6中第2步)，拱脚和拱底处出现了剪切塑性区，核心土出现了拉伸塑性区；随着开挖，拱肩处出现了剪切塑性区，拱脚处的塑性区逐渐向边墙处扩展，最终拱脚和拱底处产生的塑性区深度约为6 m。2)0∶1模型(全砂地层)，开挖前拱部处出现剪切塑性区；随着开挖进行，两侧拱脚处出现剪切塑性区，向边墙处扩展，最终塑性区深度最大处为边墙位置，为4 m。3)1∶1模型(土砂分界地层)，塑性区的发展由拱肩和拱脚处逐渐向边墙处延伸。4)单一地层中，全砂地层的塑性区发展较早，但是全土地层的发展较快；不同于单一地层模型，1∶1模型在第3、4步中，分界面处围岩先出现塑性区，且1∶1模型的最终塑性区分布与0∶1模型更为接近，与前述变形分析中“1∶1模型位移值与0∶1模型更为接近”的结论相同。

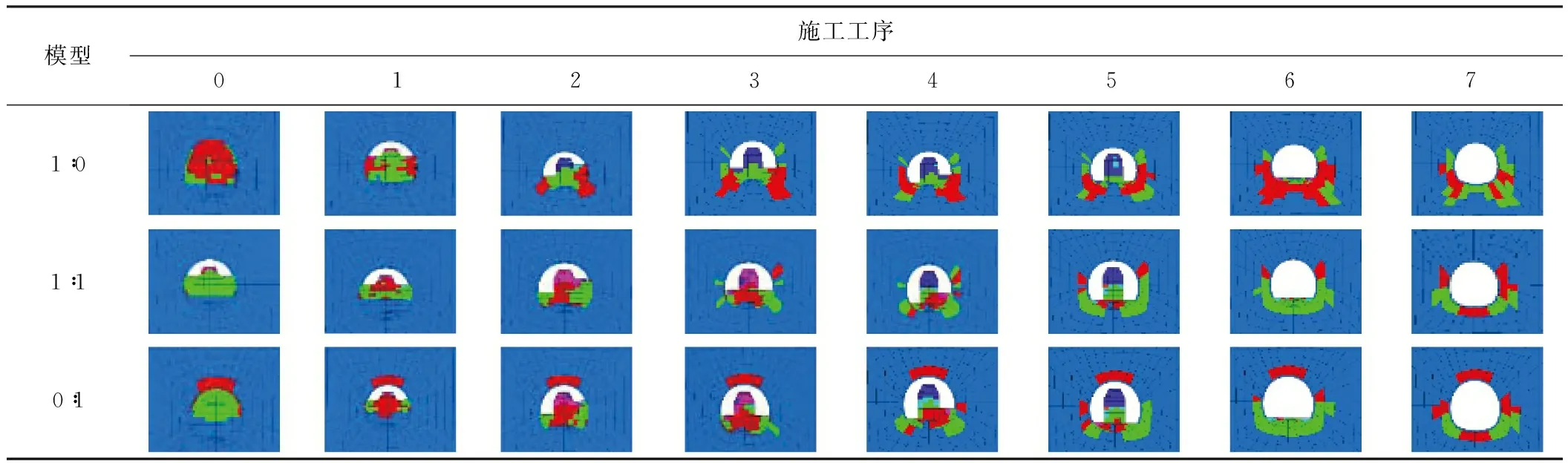
表6 三台阶七步法各工序下隧道围岩塑性区变化Table 6 Variations of surrounding rock plastic zone under different construction sequences of three-bench seven-step method

注：0表示开挖到掌子面前方；1表示开挖上部弧形导坑；2表示开挖中台阶左侧；3表示开挖中台阶右侧；4表示开挖下台阶左侧；5表示开挖下台阶右侧；6表示开挖核心土；7表示开挖仰拱。同表9。

4.2.3 支护结构应力分析

隧道支护结构受力直接影响隧道施工安全，初期支护应力曲线如图11所示。

由图11可知，土砂分界地层支护结构产生的最大主应力(不论是拉应力还是压应力)均较小，主应力差随着土层向砂层的转化(1∶0-1∶1-0∶1)逐渐减小，且在拱顶处受较大的拉力。前文对比分析了1∶1土砂分界地层与单一地层围岩稳定性，下文将在所得结果基础上改变土层与砂层相对厚度比，对土砂分界地层围岩稳定性进行探究。

(a) 各台阶处最大主应力 (b) 各台阶处主应力差 (c) 拱顶处主应力

图11土砂分界支护结构应力曲线
Fig.11 Stress curves of supporting structure in soil-sand strata

4.3 1∶3-1∶1-3∶1模型围岩稳定性探究

在1∶1模型的基础上，设置1∶3模型和3∶1模型，探究土砂分界地层土层与砂层相对厚度对围岩稳定性的影响，分析其围岩变形、塑性区扩展及支护结构受力变化。

4.3.1 围岩变形分析

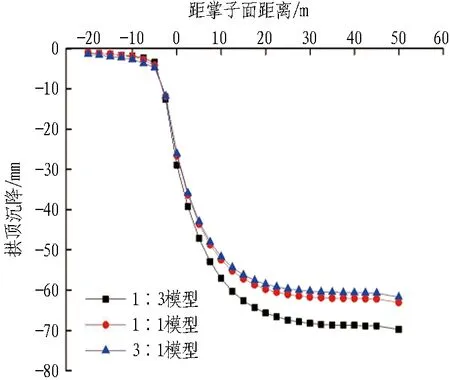
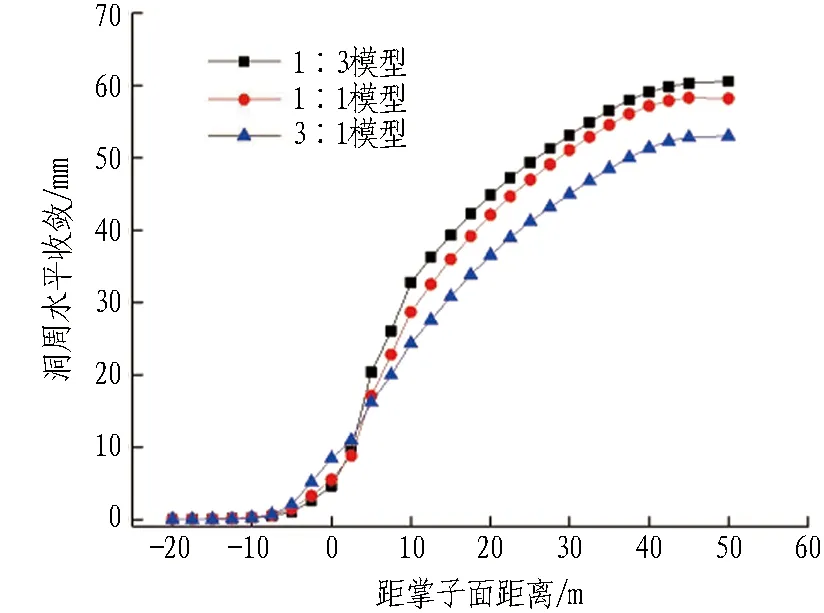
1∶3-1∶1-3∶1模型土砂分界围岩变形时程曲线如图12所示。由图可知：1)拱顶沉降的趋势与前述结果一致，但是不同相对厚度比的土砂分界地层，沉降趋于稳定的时间并不一致，1∶1模型和1∶3模型在核心土开挖前趋于稳定，而3∶1模型沉降趋于稳定在35 m左右，即核心土开挖后。 2)拱顶沉降与洞周收敛位移值为1∶3模型>1∶1模型>3∶1模型。 3)软硬互层围岩的性质取决于较软弱围岩。如前所述，在黏聚力上砂劣于土，1∶1模型洞周收敛与0∶1模型接近；在弹性模量上土劣于砂，1∶1模型拱顶沉降与1∶0模型更为接近。3∶1模型由于掌子面土占的比例更大、土对拱顶沉降影响较大，其拱顶沉降与1∶1模型较为接近；而1∶3模型由于掌子面砂占的比例更大、砂对水平收敛影响较大，其洞周收敛与1∶1模型更为接近。土砂分界地层围岩各台阶变形时程曲线及40 m断面处围岩变形最终收敛值分别如图13和表7所示。

(a) 拱顶沉降时程曲线

(b) 拱腰收敛时程曲线

图13 1∶3-1∶1-3∶1模型土砂分界围岩各台阶变形时程曲线Fig.13 Time-history curves of bench deformation of surrounding rock in 1∶3-1∶1-3∶1 model of soil-sand strata

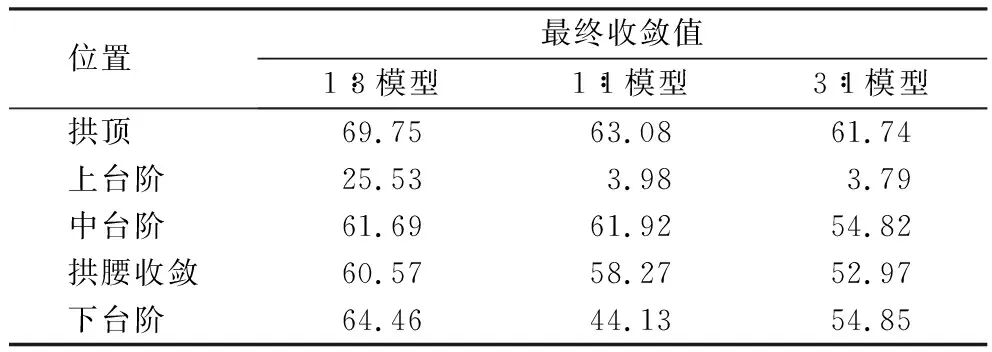
表7 1∶3-1∶1-3∶1模型40 m断面处围岩变形最终收敛值Table 7 Final convergences of surrounding rock deformation at 40 m cross-section in 1∶3-1∶1-3∶1 model mm

图13中，1∶3、1∶1、3∶1模型土砂分界面分别位于上台阶、中台阶及下台阶处。分析图13和表7可得：1)1∶3模型上、中、下台阶的洞周收敛均大于其他2个模型，且下台阶处位移明显大于中台阶处。 2)1∶0、1∶1及0∶1模型洞周收敛为：中台阶>下台阶>上台阶，而1∶3模型和3∶1模型洞周收敛位移为：下台阶处>中台阶处>上台阶处。 3)上台阶水平收敛，1∶3模型>1∶1模型>3∶1模型；中台阶水平收敛，1∶3模型>1∶1模型>3∶1模型；下台阶水平收敛，1∶3模型>3∶1模型>1∶1模型。 4)3∶1模型，由于分界面出现在下台阶，出现了变形突变的情况；1∶3模型，由于分界面的存在，上台阶处水平收敛明显大于另外两者。同样在中台阶处，1∶1模型的水平收敛也较另外两者大。 5)随着分界面下移，即掌子面土比例逐渐增大，除去分界面所处位置的突变情况，其余2个模型均因分界面下移使得各项净空收敛在减小。 6)随着分界面上移(3∶1-1∶1-1∶3)，洞周收敛与拱顶沉降之间的差值逐渐缩小。

由以上分析得出：分界面位置处变形均较突出，故需要在分界面位置处进行加固处理；分界面位置对拱顶沉降与洞周收敛间的相互关系有一定影响。

表8所示为各施工阶段变形占总变形量的百分比。由表可以得到，拱顶沉降大都集中在上、中台阶开挖，中台阶开挖对洞周收敛的影响最大。从1∶3-1∶1-3∶1模型，分界面逐渐下移，上、中台阶开挖造成的水平收敛速率逐渐减小，下台阶和核心土开挖造成的收敛速率逐渐增大，仰拱封闭前洞周收敛和拱顶沉降均达到了98%以上。隧道开挖过程中分界地层分界面位置对收敛速率有一定影响，接近土层分界面位置的收敛速率较大，但并不改变中台阶开挖对洞周收敛影响最大的结论。

4.3.2 围岩塑性区分析

表9所示为三台阶七步法不同施工工序下隧道围岩塑性区变化。由表可得：1)1∶3模型在上台阶开挖后，核心土上部出现拉伸塑性区、下部仅有剪切塑性区；中台阶左侧开挖，拱脚处出现塑性区，中台阶开挖完成后迅速在分界面下侧形成较长范围塑性区，拱脚处塑性区也加速扩展；核心土开挖前，分界面下侧塑性区已从深度2 m扩展到4 m；隧道贯通后，从拱脚到分界面处产生深度超过4 m的塑性区，范围与拱底相当。2)3∶1模型在第3步时，在左边墙、右拱脚及右拱肩处出现塑性区，第4步中(开挖下台阶左侧时)分界面上部边墙处、下部拱脚处塑性区迅速扩展，最终在拱底到两侧拱肩间形成深度2 m以上的塑性区。3)相比于1∶1模型，1∶3模型和3∶1模型在分界面附近边墙处塑性区的发展较早且迅速，1∶3模型边墙塑性区在第2—4步中发展迅速，3∶1模型边墙塑性区在第3—4步中发展迅速，而1∶1模型边墙塑性区在第4—5步中发展迅速。4)3个分界地层模型中，1∶3模型塑性区深度最大且发展最快。

表8 1∶3-1∶1-3∶1模型各施工阶段变形占总变形量的百分比Table 8 Proportions of deformation of every construction phase in 1∶3-1∶1-3∶1 model in total deformation

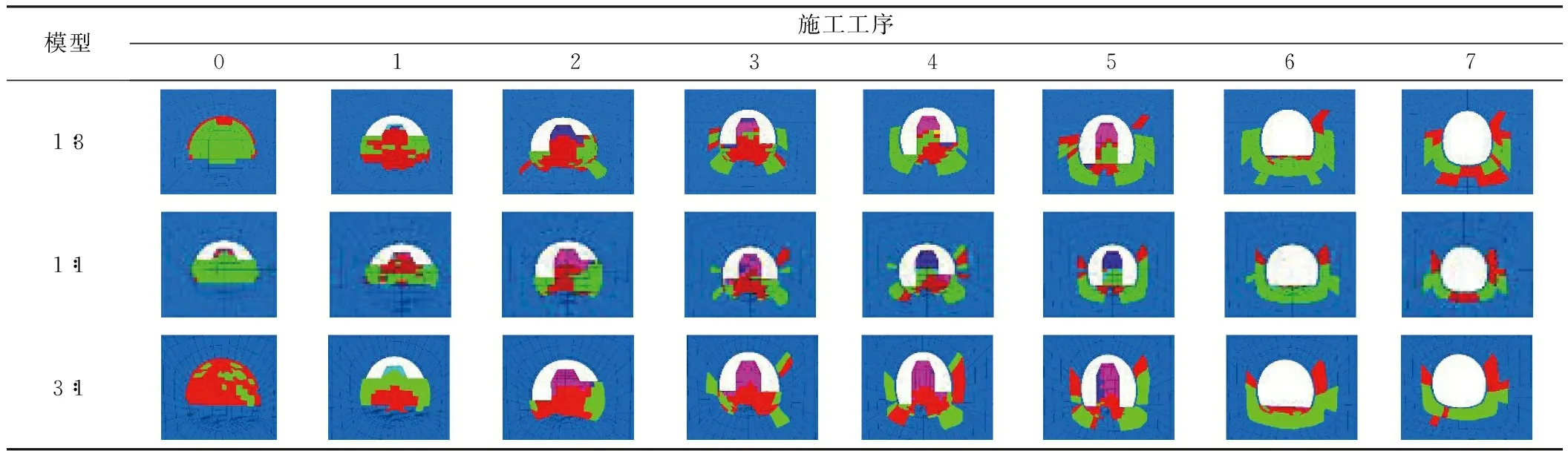
表9 1∶3-1∶1-3∶1模型各工序下隧道围岩塑性区变化Table 9 Variations of surrounding rock plastic zone under different construction sequences in 1∶3-1∶1-3∶1 model

4.3.3 支护结构应力分析

随着土砂分界面的下移，中台阶、下台阶处初期支护最小主应力不断减小，上台阶处最小主应力不断增大。支护结构最大主应力随施工工序变化曲线见图14。

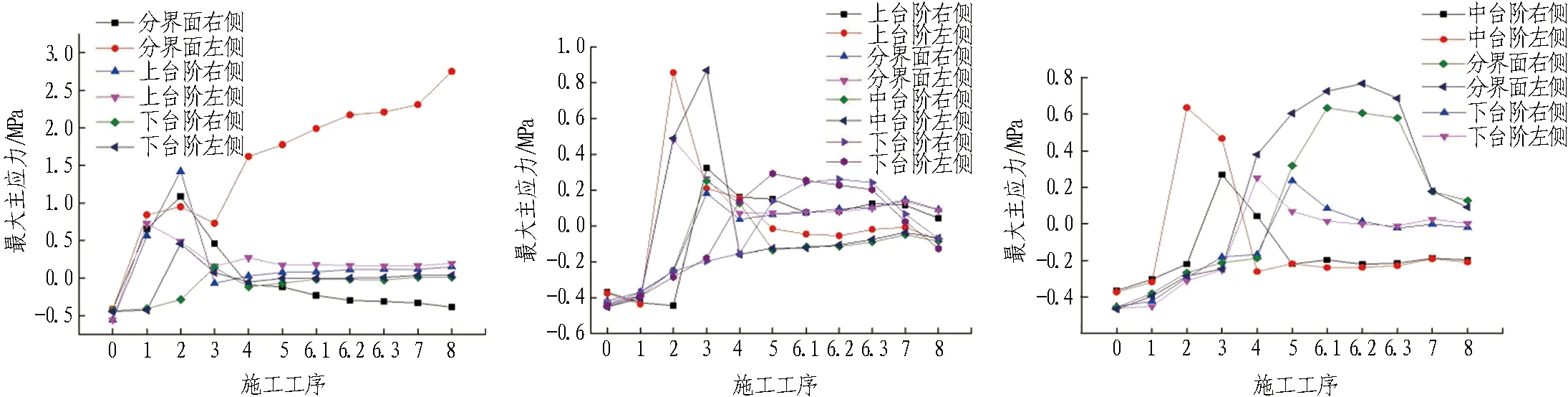
(a) 1∶3模型 (b) 1∶1模型 (c) 3∶1模型

图14支护结构最大主应力随施工工序变化曲线
Fig.14 Variation curves of maximum principal stresses of supporting structure with construction procedures

由图14可得：1)3个模型均在分界面处会产生拉应力。2)观察图(a)会发现，在分界面处左侧(先开挖侧)产生了持续增长的拉应力，而在右侧则产生了很大的压应力，且分界面所在位置产生的拉应力远大于上台阶、拱腰处；图(c)中，分界面所在位置支护结构产生的拉应力也超过了其附近中台阶和拱脚处的值。3)观察三者的最大主应力变化趋势，1∶1模型中的上台阶和下台阶分别在第2、3步和第5、6.1步达到峰值，平均值分别为0.6 MPa和0.25 MPa；1∶3模型中的上台阶在第1、2步工序时达到峰值，平均值为1 MPa；3∶1模型中的下台阶最大主应力峰值出现在第4、5步，平均值为0.7 MPa左右，分界面的存在影响到了应力发展。

支护结构最大主应力如图15所示。由图可知：1)1∶3-1∶1-3∶1模型，拱顶、拱肩、拱底处的最大主应力呈现减小的趋势。2)相比较其他模型而言，分界处及其所在台阶处的支护结构最大主应力较大。

综上，由于分界面的存在，对分界面处及所在台阶位置的初期支护结构的应力产生了较大的影响，在施工过程中需要对分界面位置进行重点监测。

(a) 拱顶、拱底最大主应力 (b) 分界面处最大主应力 (c) 台阶处最大主应力

图15支护结构最大主应力
Fig.15 Maximum principal stresses of supporting structure

5 现场监控量测试验

选取阳城隧道1#斜井正洞小里程方向，监控量测断面为DK244+855、DK244+515、DK245+130和DK245+260。DK244+855断面上层为砂质新黄土，约占掌子面的60%；下层为富水全风化红砂岩，约占40%。DK244+515断面，掌子面上部分布有少量的砂质黄土，约占25%；下部为全风化砂岩夹块石。DK245+130断面，掌子面上部为土夹薄砂层，占20%；下部为全风化红砂岩。DK245+260断面，掌子面上部为砂质老黄土，占16%；下部为全风化砂岩夹少量块石。现场沉降监控量测如图16和表10所示。

(a) 拱顶沉降时态曲线

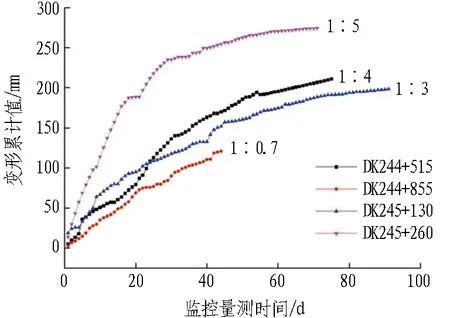
(b) 拱腰收敛时态曲线

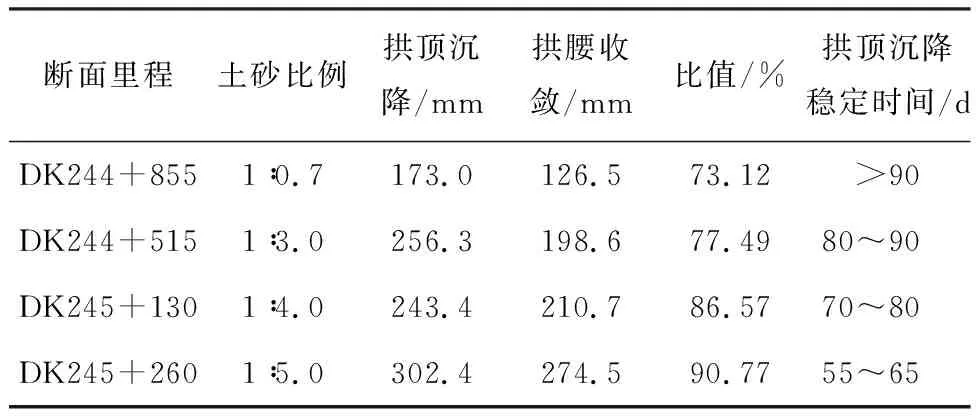
表10 各断面沉降收敛值Table 10 Final convergences of every cross-section

注：比值=拱腰收敛/拱顶沉降×100%。

由表10可知，监控量测结果与数值模拟结果规律相同，即随着分界面的下移(即土占的比例的增多)，初期支护的变形在减小，且随着分界面的上移，拱顶沉降和水平收敛的差距在不断减小，与数值模拟规律相类似，印证了前文中所述的“稳定滞后”现象的存在。钢拱架钢筋应力最大值如表11所示，随着分界面的上移，拱底、拱顶钢拱架内力值增大，与前述的规律相同。

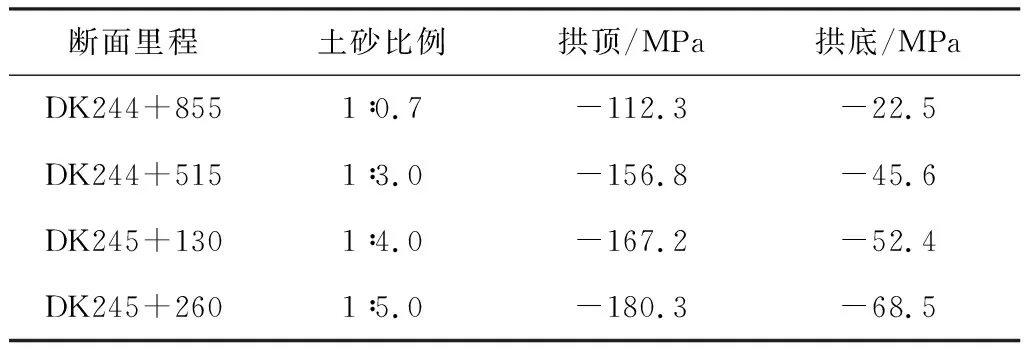
表11 钢拱架钢筋应力最大值Table 11 Maximum stress of reinforced bars of steel frame

6 结论与讨论

铁路大断面隧道穿越土砂分界地层，洞周围岩变形及初期支护内力与土砂分界的土石比例有着密切的联系，通过分析可知：

1)土砂分界地层分界面的存在对围岩周围的主应力分布产生了较大的影响，产生了不同程度的“下垂”状态。当从全土层向全砂层转变，拱顶沉降出现了“稳定滞后”的现象。分界地层相比于单一地层，在开挖分界面位置处边墙极易出现塑性变形，产生塑性区。

2)针对分界面位置的改变，对照监控量测数据，可以看出实际工程中结构收敛与数值模拟规律相同。即随着全风化砂占的比例的增大，拱顶沉降和洞周收敛都在变大，且部分水平收敛与拱顶沉降的差值会越来越小，甚至是超过拱顶沉降值。

3)开挖模拟中，相比于其他地层条件下相同位置，分界面所处的位置处会产生较大的水平收敛，且分界面处会极易产生拉应力。分界面的存在对于支护结构的应力发展产生了较大的影响，主要体现在到达峰值的时机。

4)当分界面出现在掌子面上部时，支护结构会产生极大应力和较大的变形，围岩会产生极大的塑性变形，且边墙部位的塑性区发展迅速。

5)三台阶七步法开挖过程中，拱顶沉降发展主要集中在上、中台阶开挖阶段，而水平收敛发展主要在中台阶开挖阶段；分界面的下移会导致上、中台阶开挖造成的水平收敛速率减小，使下台阶开挖造成的水平收敛速率增大；由于开挖顺序的影响，左侧和右侧应力分布会产生较大的差异。施工过程中可根据左右侧土体的差异来调整左右开挖顺序。

6)本文仅针对分界地层下的层厚比进行了研究，仅对分界地层围岩稳定性进行了定性分析，关于定量分析还需要今后进一步研究。