多管齐下解决高斯定理教学中的问题*
2018-11-06王洪涛李艳
王洪涛 李艳
(中国矿业大学物理学院 江苏 徐州 221116) (2018-04-04)
大学物理课程是本科教育阶段的一门重要的公共基础课程,课程具有知识量大、理论性强、结论抽象等特点.电磁学部分由于理论抽象、计算过程需要用到相对复杂的微积分知识等特征,致使学生在理解掌握知识上存在一定的困难.实际教学过程中经常性会遇到部分学生对传统的定理推导过程抱有疑问,他们更倾向于采用“笨一点”的方法来思考问题.比如电场的高斯定理,该定理是计算规则对称分布电场的有力工具,但是总有部分学生提出能不能利用前面学过的点电荷的电场强度叠加方法得到均匀带电球体或球面在周围任意一点的场强?学生的疑问其实暴露出了一定的问题,即学习知识的惯性思维,每当学到新知识的时候往往还希望尝试用已熟练掌握的知识去解释、推导及验证.基于此,在讲授新知识的时候可以根据教学进度分层次地引导学生进行验证探索,这对学生深入理解掌握物理知识、复习应用数学及计算机知识都有很大的益处.
本文以静电场中的高斯定理为例,采用“笨方法”——点电荷场强的积分方法和“小高招”——数值编程模拟方法对高斯定理进行验证,使学生从不同角度不同层次上理解掌握知识.
1 高斯定理计算场强
采用高斯定理[1]计算均匀对称分布电场的电场强度是大学物理中计算场强的重要方法之一,均匀带电的圆球面在球面[2]及其周围激发的电场具有均匀对称分布的特点,是高斯定理应用的常见情况.设球面半径为R,电荷密度为σ,写出高斯定理的具体表达式为[3]
(1)
由此易解出距球心为x处的一点的电场强度为
(2)
2 矢量叠加法计算场强
通过点电荷电场的矢量叠加方法理论上可以直接积分求解任意带电体周围激发的电场.对于具有圆对称性的带电球面,可以通过合理划分微分单元把一般的三维体积分简化为一维线积分来处理.均匀带电圆环在轴线上距圆心x的点的电场强度为
(3)
其中q为圆环所带电荷,R为圆环半径,x为场点距带电圆环圆心的距离.可以把带电球面沿垂直x轴方向分割为若干个半径连续变化的同轴圆环,如图1所示.以球心为坐标原点,水平向右为x轴方向建立坐标系.
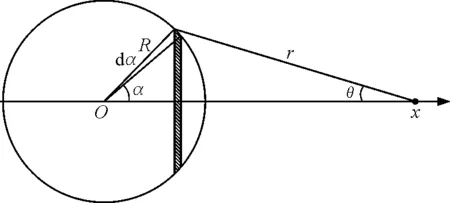
图1 带电球面微分单元划分示意图
用夹角α表示微分元圆环的位置,则圆环所带电荷为
dq=σRdα2πRsinα
其在x点的场强为
通过对α积分可以得到带电球面在距球心x处的电场强度表达式
(4)
对式(4)进行化简,令β=x2+R2-2xRcosα则可得到
(5)
其中
β1=(x-R)2
β1=(x+R)2
通过“笨一点”的积分方法得到结果与高斯定理得到的结果完全一致,不仅验证了高斯定理的正确性打消了学生的疑虑,使学生对微积分方法在大学物理学习中的灵活运用有了更深入的理解和体会,同时也说明点电荷电场强度的叠加原理对任意带电体的电场计算都是适用的,区别只在于积分计算的难易.
3 数值编程模拟
物理学知识理论性较强,结论定理大都比较抽象.可以通过计算机编程把抽象的公式定理用直观的图线演示出来,增强学生对知识的掌握[4].积分的数值编程方法有很多,学生在数学及计算机课程上都有所涉及,通过计算机编程模拟不仅可以把抽象的知识形象化,而且能够借此让其了解数学及计算机编程手段的应用,可谓一举多得.编程语言有很多,常见的有Matlab,C++,Fortran,Python等等,虽然在代码书写上存在一些差异,但是算法是共通的.Python 是一种不受局限、跨平台的开源编程语言,它功能强大且简单易学,代码简洁易懂,目前在很多行业已得到广泛应用.数值编程模拟的主要目的是验证定理结论或对抽象知识进行形象化展示,因此对运算速度及精度要求不高,可以采用经典的梯形法计算积分[5], Python程序积分代码如下:
#------------------
import math
sigma = 1e-8
epsilon = 8.854187817e-12
R = 0.2; x = 0.4; a = -1; b = 1; h = 2.0/16000; s = 0; m = a; f0 = 0
for i in range(16000):
m += h
f1 = (sigma*R**2/2/epsilon)*(L-R*m)/(L**2+R**2-2*L*R*m)**1.5
s += h*(f0+f1)/2
f0 = f1
print(x,s)
#-------------------
为了考察积分区间[-1,1]划分子区间的数目与计算精度的关系,程序连续计算了子区间数目分别为1 000, 2 000,…,16 000共16组数据,并把计算结果与公式(2)进行了对比,求出其相对误差,如图2所示,其中横轴为等分区间数目N,纵轴为模拟值与理论值的相对误差.由图可以看出,随着等分区间数目的增加,计算结果很快收敛于理论值.当等分区间数目为N=7 000时,相对误差已降至5×10-5以下.梯形积分法编程简单,计算精度较高,能够满足教学验证及学生课下实践的要求,在增加对物理知识的理解及对抽象知识的直观展示方面具有积极意义,适合在大学物理教学过程中推广应用.

图2 相对误差与积分区间等分数目的关系
取N=16 000,R=0.2 m固定不变,场点距球心坐标由近及远连续变化,x=1.2R,1.4R,…,4.0R,通过积分程序分别计算得到对应x距离下的电场强度,把x及对应电场强度数据存入数据文件“E.data”中,然后利用Gnuplot进行绘图.Gnuplot是免费开源的科学绘图软件,具有很强的数据绘图及参数拟合能力[6],同时支持交互和脚本两种工作模式,在输出图片的高质量和高可控性上有较强的优势.在Gnuplot中写入下述命令:
sigma=1e-8; R=0.2; epsilon=
8.854 187 817e-12
f(x)=sigma*R**2/(epsilon*x**2)
plot f(x) with line, ‘E.data’ using 1:2 with point

图3 理论结果与数值模拟结果对比图
4 小结
本文针对电场高斯定理教学实践中的问题,通过点电荷场强积分方法计算了均匀带电球面周围的电场分布,并且采用开源、高效的程序语言Python及科学绘图软件Gnuplot对电场分布进行了数值模拟.采用多管齐下的方法使学生从不同角度对高斯定理展开了全面深入的学习和理解,不仅促进了学生对物理知识的掌握,而且让他们体会到了微积分及数值编程知识在物理学习过程中的具体应用.采用Python及Gnuplot开源软件实现抽象物理知识的直观形象化在教师教学实践及学生课下探索过程中具有很高的可执行性,值得在大学物理教学中进行推广和应用.
