基于等几何边界元法的声学敏感度分析
2018-11-05赵文畅陈磊磊陈海波
刘 程, 赵文畅, 陈磊磊, 陈海波*
(1.中国科学技术大学 近代力学系 中国科学院材料力学行为和设计重点实验室,合肥230027;2.信阳师范学院 土木工程学院,信阳464000)
1 引 言
随着计算机技术的应用与普及,CAD与CAE技术在工程领域得到了长足的发展。非均匀有理B样条(NURBS)在过去数十年成为了几何造型领域应用最广泛的造型工具,在曲线曲面建模中有突出优点。可以精确表示二次规则曲线曲面,从而能用统一的数学形式表示规则曲面与自由曲面;具有可影响曲线曲面形状的权因子,使形状更易于控制和实现。在CAE领域,运用最广泛的模型描述语言多是网格语言,随着工程问题呈现出大而复杂的特点,传统的网格数据越来越庞大,使得产品设计与分析割裂开来。Hughes等[1]提出了等几何分析方法,利用NURBS基函数替代传统的拉格朗日插值函数,统一CAD和CAE的描述语言,建立起产品设计与分析的桥梁。
作为经典的CAE数值方法之一,边界元法在某些特定的领域如无限域问题中展现出了卓越的性能。传统边界元法在结构边界处划分网格,同样会遇到设计和分析模型描述语言不融合的问题。近些年,等几何边界元法得到了快速发展,已在弹性力学[2]、位势问题[3,4]、断裂力学[5,6]、声学[7-9]和形状优化[10,11]等领域取得了重要的研究成果。在声学领域,Burton-Miller方 法[12,13]可 以 避 免 边 界元法在求解外声场问题中遇到解的非唯一性现象,但该方法具有超奇异积分问题,文献[7,8]用正则化算子消除了等几何边界积分方程中的超奇异性。本文不同于以往,选取奇异性相消技术[14],并结合Cauchy主值积分和Hadamard有限部分积分,推导出直接计算超奇异积分项的半解析表达式。
声学敏感度[15]表征声学物理量对设计变量的变化率,可以用来决定设计变量的优化方向,因此敏感度信息是基于梯度优化方法的重要基础。传统网格划分中,网格节点的敏感度信息往往难以实现结构的整体形状优化,而等几何分析方法将形状优化对象转化为建模时的控制点坐标,优化过程中可以灵活控制几何形状,避免了网格重新划分等问题。本文以NURBS控制点坐标为设计变量,利用直接微分法[16-18]推导出等几何敏感度边界积分方程,直接求出域内声压对控制点坐标的敏感度,从而找到结构形状与域内声压分布之间的对应关系,为进一步的声学结构形状优化做好准备。针对敏感度分析的超奇异积分问题,将采用等几何边界积分方程中相同的处理方式,以保证计算效率与精度。
2 NURBS基函数
NURBS插值基函数通常建立在B样条基函数的基础上,二维形式定义如下[3],
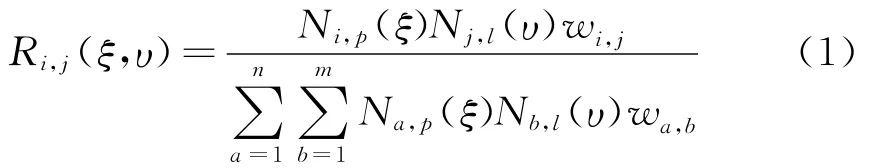
式中 N 为一维B样条基函数,可以看出,Ri,j(ξ,υ)是由两个一维B样条基函数通过张量乘积的形式组合得到,这两个B样条基函数分别定义在节点矢量Ξ=[ξ1,ξ2,…,ξn+p+1]和Υ=[υ1,υ2,…,υm+l+1]上,其中p和l分别为两个方向上的基函数阶次,n和m分别为两个方向上的基函数数目,wi,j为权重。
NURBS基函数继承了B样条基函数非负性、紧支性以及归一性等良好的数学特性,给定控制点Pi,j,则 NURBS曲面可表示为
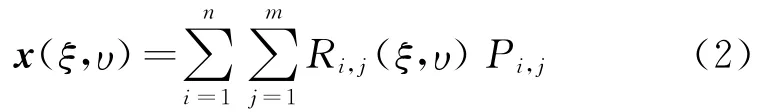
NURBS可以精确构造二次规则曲面,如典型的球面。控制点Pi,j和权重wi,j一一对应,可灵活控制结构形状。另外NURBS曲面的法向导数和雅可比系数均可以解析表达,因此几何信息是完全精确的,有助于提高计算精度。
3 三维声场等几何边界元法
3.1 等几何边界积分方程
三维声场的控制方程为Helmholtz方程,通过格林第二等式变换,并将源点置于边界上,得到边界积分方程
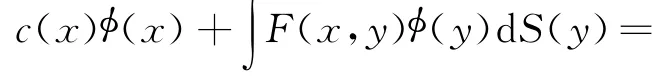
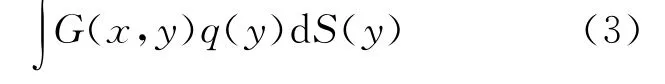
式中 x为源点,y为场点,∮为声压,q=ɸ∮/ɸn为声压法向通量;若边界光滑,c(x)=1/2;核函数G(x,y)=eikr/(4πr),k为波数,r=|x-y|;核函数F(x,y)=ɸG(x,y)/ɸn(y)。采用 Burton-Miller法处理解的非唯一性问题[12],则法向导数边界积分方程为
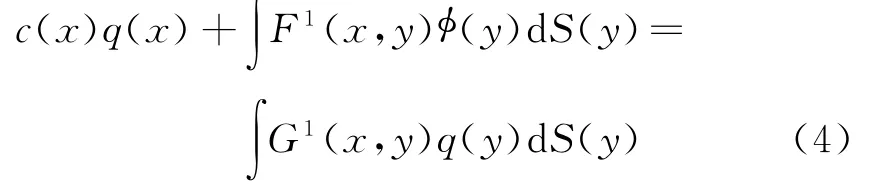
式中 G1(x,y)=ɸG(x,y)/ɸn(x)
F1(x,y)=ɸF(x,y)/ɸn(x)
采取配点法求解方程(4),配点坐标为Greville坐标[2]。边界上的∮和q用NURBS基函数插值得到。
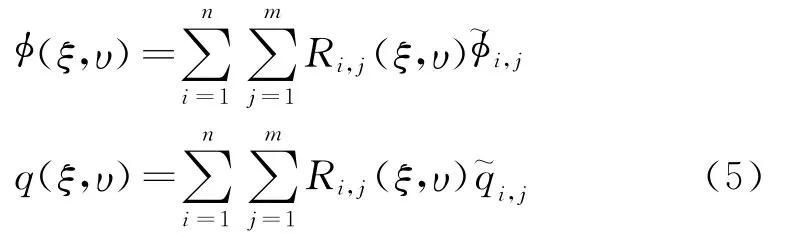

式中
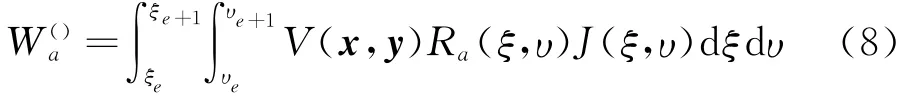
其中 中的V(x,y)依次表示核函数G,F,G1和F×表示一个积分单元。用Burton-Miller法组合式(6,7),得到线性代数方程组

式中 H和G为积分项求得的系数矩阵,Φ~和q~分别为配点处声压系数与声压通量系数列向量,将所有未知值移到方程左边,已知值移到方程右边,求解该方程,即可得到边界未知物理量。
3.2 奇异积分处理
式(6,7)的积分可由 Gauss-Legendre积分计算,但当源点参数坐标满足×[υe,υe+1]时,式中的积分出现奇异现象,这时需要特殊的处理方式才能正确计算这些奇异项。
式(6)中核函数G为弱奇异性,极坐标变换即可消除奇异性,自然坐标 (ξ,υ)与极坐标 (ρ,θ)对应关系为

坐标转换完成后,式中积分项简写为
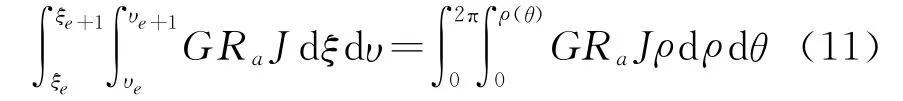
式(11)右边可直接用Gauss-Legendre积分计算。
核函数F和G1形式上具有强奇异性,但均含有ɸr/ɸn项,该项在r→0时也趋于0,因此也是弱奇异性的,相应积分经极坐标变换后可直接由Gauss-Legendre积分计算。
由于F1为超奇异,单纯的极坐标变换无法消除奇异性,借助Guiggiani等[14]提出的结合Cauchy主值积分和Hadamard有限部分积分的奇异相消技术,可直接计算该类积分。核函数F1中超奇异项为nl(x)nl(y)/4πr3,极坐标转换后该项可展开为

根据Cauchy主值积分和Hadamard有限部分积分
法,包含F1的奇异积分项可表示为

式(13)各项均为无奇异项,可由 Gauss-Legendre积分直接计算,其中β(θ)和γ(θ)的表达式可参考文献[14],接下来确定f1(θ)和f2(θ)的具体表达式即可。
将NURBS插值基函数在源点处泰勒展开为
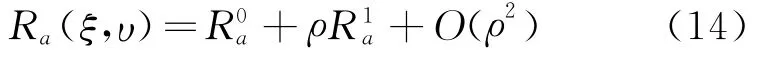
同理nl(x)nl(y)J(y)在源点处泰勒展开为

另外,r-3可展开为

式中 S3(θ)和S2(θ)的具体表达式与文献[14]相同。将式(14~16)代入式(12)等号左边得,
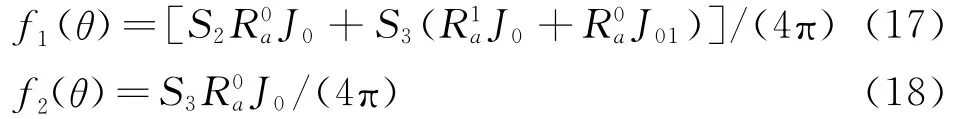
4 对控制点的敏感度分析
4.1 等几何敏感度边界积分方程
边界物理量的敏感度由NURBS函数插值得
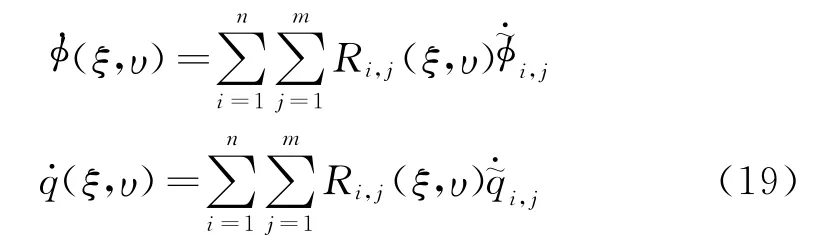
将式(3,4)对设计变量求导,并将式(2,5,19)代入,得到离散形式的等几何敏感度边界积分方程
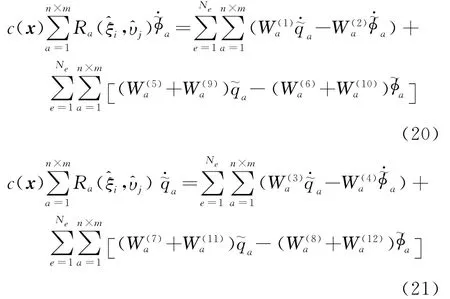
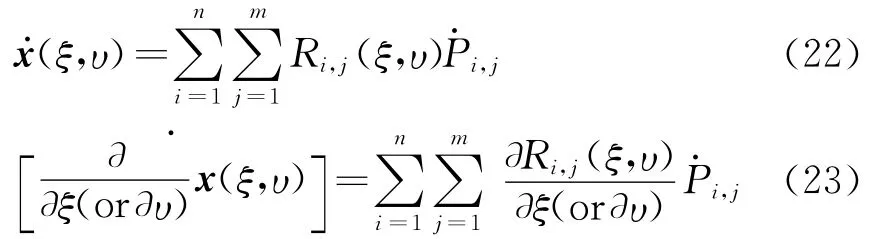
用Burton-Miller法组合式(20,21),得到线性代数方程组,写成矩阵形式为
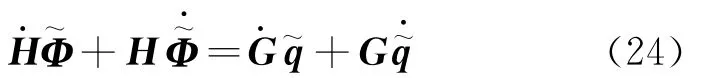
4.2 奇异积分处理
对于式(20,21)的奇异积分,同样采用3.2节的处理方式。包含核函数G,F,,,G1以及的奇异积分项均为弱奇异,采用极坐标变换方式即可得到正确数值积分结果。包含F1的超奇异积分项处理方式同3.2节,包含的超奇异积分项的具体处理方式如下。
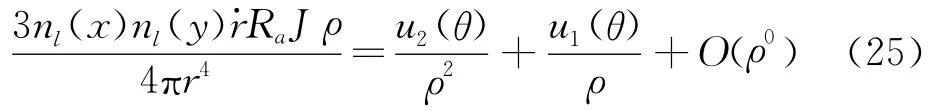
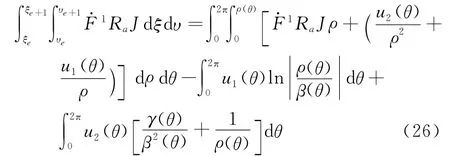
式中各项可由Gauss-Legendre积分直接计算,β(θ)和γ(θ)与3.2节一致,u1(θ)和u2(θ)同样由泰勒展开的方式确定。
将式(26)左边各项作泰勒展开,与文献[14]主要不同之处是r·的展开表达式,
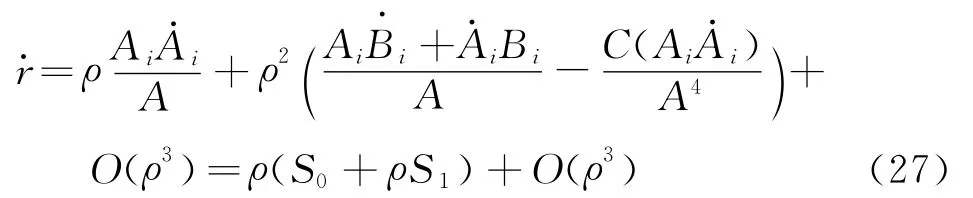
式中 Ai,Bi和A均为θ的函数,与文献[14]一致,C=AiBi。A·i和B·i分别为Ai和Bi对设计变量的敏感度,均可通过NURBS基函数插值显式表达。S0和S1分别为式(27)中ρ对应阶次前的系数。另外,r-4可展开为[14]
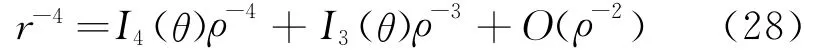
式中
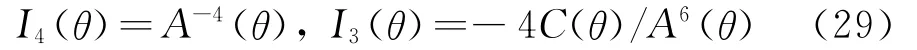
将式(14,15,27,28)代入式(25)左边,最终得到u1(θ)和u2(θ)的表达式为
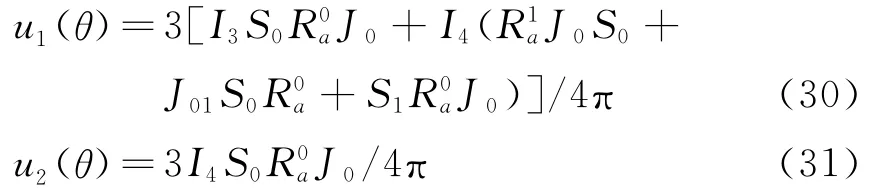
5 数值算例
5.1 脉动球的声辐射
以典型的脉动球辐射算例来验证本文推导的公式。本文所有的计算过程均在台式计算机上用Fortran90编程实现,计算机配置为Intel Core i7 CPU和16GB内存,为了提高效率与保证精度,本文用于Gauss-Legendre积分的点数目在非奇异积分情况下为6×6,奇异积分时为10×10。
声传播介质为空气,密度为1.2kg/m3,声波速度为340.0m/s。如图1所示,该球面上各点以速度vn做同振幅同相位的振动,球体振动会在周围介质中引起声辐射。设已知边界条件为Neumann边界条件,边界声压法向通量值q=1509.6i。整个球面通过NURBS曲面构造,半径为1.0m。控制点信息如图2所示,共26个控制点,参数ξ与υ方向的阶次均为2,节点矢量分别为Ξ={0,0,0,0.5,0.5,1,1,1}和 Υ ={0,0,0,0.25,0.25,0.5,0.5,0.75,0.75,1,1,1}。
选取xoy平面内半径为2.0m的圆上等分的180点为参考点,将本文算法计算的数值解与脉动球声辐射解析解取相对误差,以考察本文算法的精度。图3为采用等几何边界元法时该算例计算误差随频率的变化关系,BM代表Burton-Miller法,自由度数为121,考察频率为50Hz~350Hz。可以看出,没有使用Burton-Miller法时,在k=π和k=2π处的计算结果严重失真;而Burton-Miller法的计算精度尽管有所降低,但在整个频段上均可以计算准确,证明该方法可以克服解的非唯一性。
图1 NURBS建模的脉动球Fig.1 NURBS model of pulsating sphere
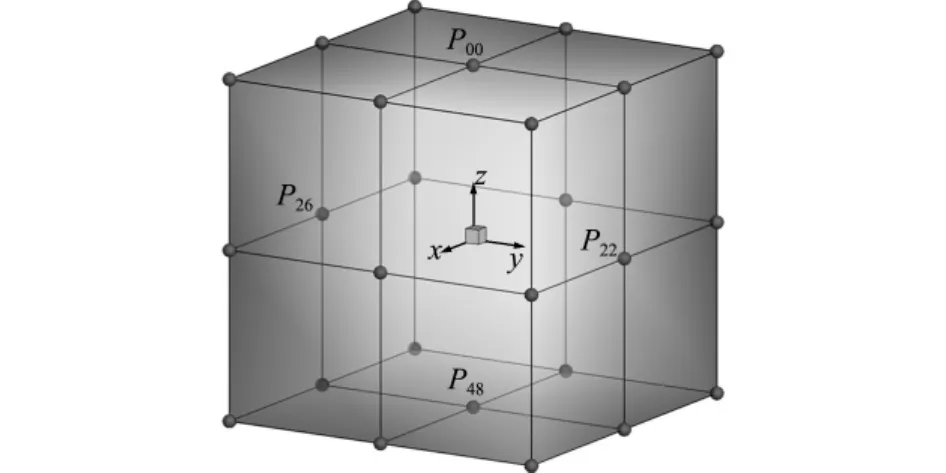
图2 NURBS球的控制点信息Fig.2 Control points of the NURBS sphere
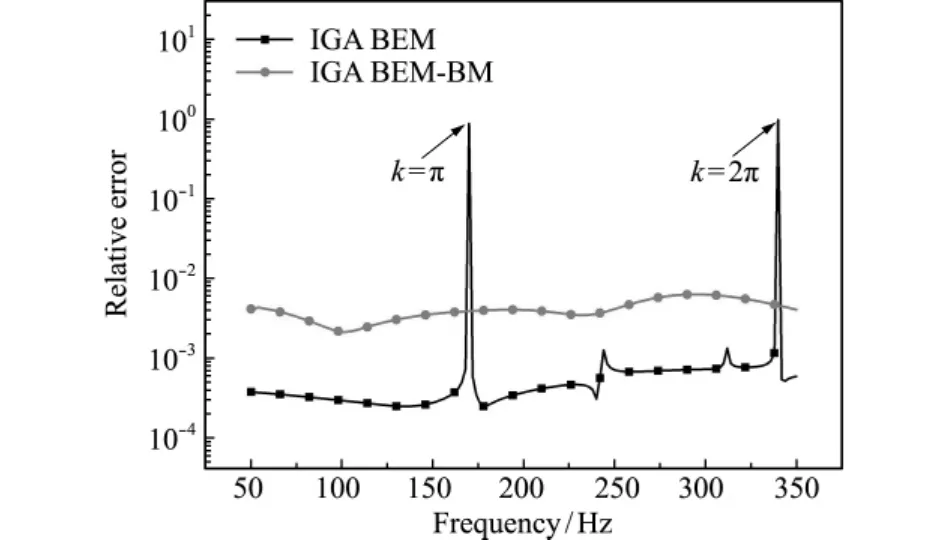
图3 等几何边界元计算误差随频率变化的关系Fig.3 Relative error of IGA BEM simulations with respect to frequencies
设计变量取图2中控制点P22的y坐标,在球体中其初始值为1.0m,考虑结构不出现交叉重叠的现象,设该设计变量取值恒为正值。由于设计变量的变化,结构将会成为不规则构型,因此声场声压敏感度值不存在解析解,本文借助有限差分法(finite difference method)来验证本文敏感度数值解的正确性。分析声频率为100Hz,计算自由度取121,有限差分步长为0.001m。图4给出了点(0,2,0)处的声压敏感度实部与虚部值随控制点P22的y坐标的变化关系,控制点P22的y坐标范围为0.5m~1.5m。可以看出,本文用直接微分法计算的结果与有限差分法的结果吻合良好,由于积分方程中的超奇异积分非常容易影响精度,而本文采取的奇异相消技术给出了半解析的直接计算公式,从直接微分法的结果来看,很好地消除了超奇异积分的影响。
5.2 不同形状脉动结构的声辐射
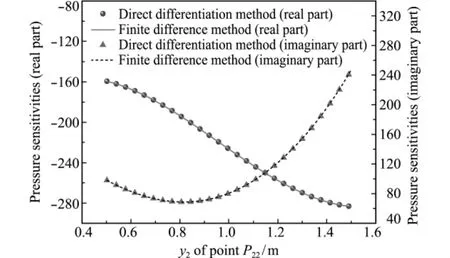
图4 点(0,2,0)处的声压敏感度值随控制点P22的y坐标变化关系Fig.4 Pressure sensitivities at point(0,2,0)with respect to the ycoordinate of P22

图5 不同几何形状脉动结构Fig.5 Different shapes of pulsating structures
NURBS构造的构型有众多控制点,每个控制点的取值不同,结构的形状就会不同。因此,本文在图2脉动球控制点的基础上,改变一些控制点的坐标取值,构造出不同几何形状的脉动结构,如图5所示。保持几种构型的几何节点矢量和权重一致,控制点坐标取值如下。(a)保持球体模型不变。(b)P22坐标取(0,0.5,0),其他控制点坐标不变。(c)P22坐标取(0,1.5,0),其他控制点坐标不变。(d)P00坐标取(0,0,1.5),P22坐标取(0,1.5,0),P26坐标取(0,-1.5,0),P48坐标取(0,0,1.5),其他控制点坐标不变。值得注意的是,若控制点重合,则重合点坐标也随之改变。
设这些结构表面各点同样以速度vn做同振幅同相位的振动,边界条件不变,以考察域内声场声压以及敏感度值的分布情况。选取半径为2.0m的球面作为考察面,分析该球面上的声压分布,以及该球面上的声压模值对P22的y坐标的敏感度值分布。分析频率为100Hz,结构自由度取121。图6给出了脉动结构各个形状下考察面上的声压模值分布,不同构型的声压值分布显然完全不同,除了数值差异较大外,各个构型上出现声压最大与最小值的位置也不同,如图6(b,c)所示,因此若要对某目标区域的声压值进行调控,在一定范围内可以通过改变结构形状来完成。形状I为规则球体,因此图6(a)考察面上声压模值完全相同。形状IV稍复杂,因此图6(d)中声压模值分布与结构上凸出的部分相关。图7给出了各个形状下,考察面上声压模值对P22的y坐标的敏感度值分布。可以看出,考察面上声压模值的敏感度分布主要为数值上的差异,但均呈现对称性带状分布。这些敏感度值表征了考察面上声压对设计变量的变化率。
5.3 水下大尺度壳体的声散射
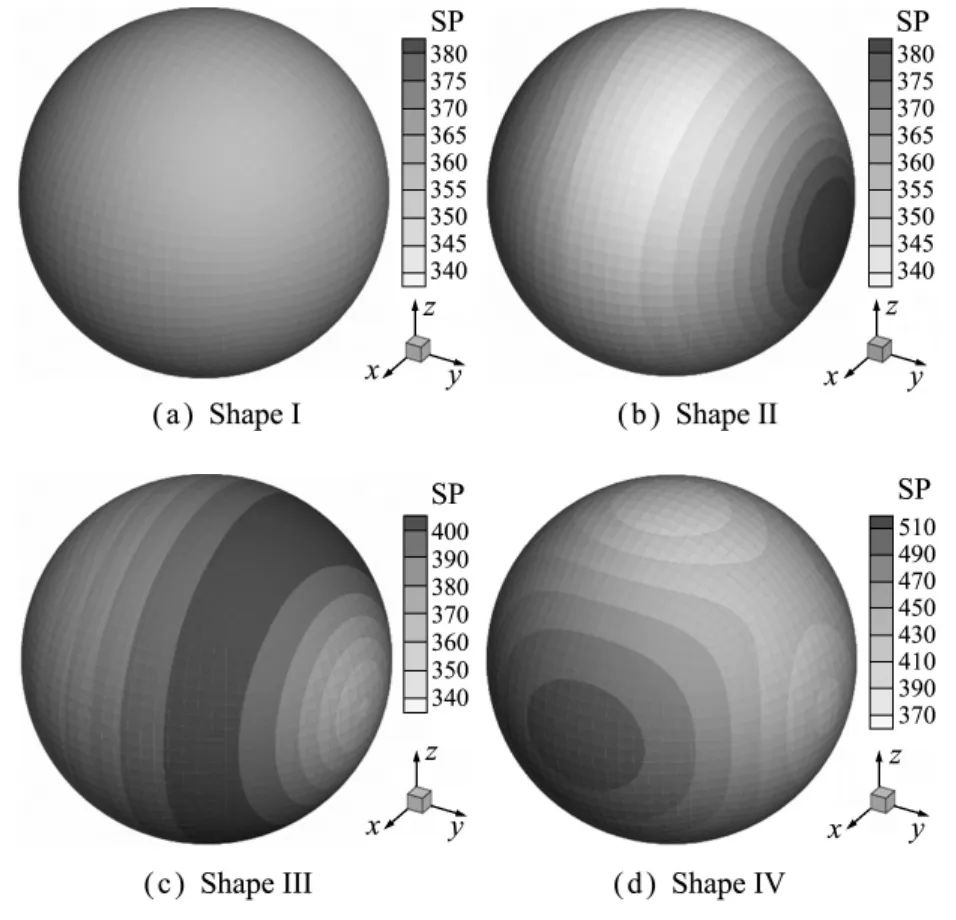
图6 不同形状脉动结构考察面上声压模值分布Fig.6 Distribution of sound pressure modulus on the reference surface with respect to different structure shapes
大尺度壳体模型的声散射数值仿真具有重要的意义,如水下潜艇声散射特性的数值仿真可以有效模拟潜艇的声学性能,为潜艇的声学设计提供必要的参考。2001年德国FWG提出标准潜艇BeTSSi-Sub(Benchmark Target Strength Simulation Submarine)的概念,Nell等[19]在这基础上作出了相关改进,艇身主要尺寸如图8所示。艇艏为半椭球体,艇体为圆柱体,艇艉为圆锥体,笛卡尔坐标系原点位于圆柱艇体的中心。将图8的模型用NURBS建模,控制点信息如图9所示,参数ξ与υ方向的阶次均为2,节点矢量分别为Ξ={0,0,0,0.25,0.25,0.5,0.5,0.75,0.75,1,1,1}和 Υ ={0,0,0,0.25,0.25,0.5,0.5,0.75,0.75,1,1,1}。
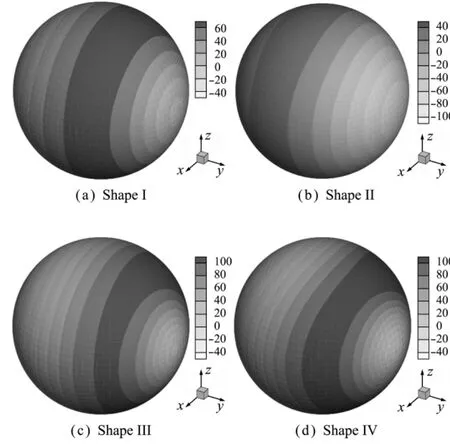
图7 不同形状脉动结构考察面上声压模值的敏感度值分布Fig.7 Distribution of sound pressure sensitivities on the reference surface with respect to different structure shapes
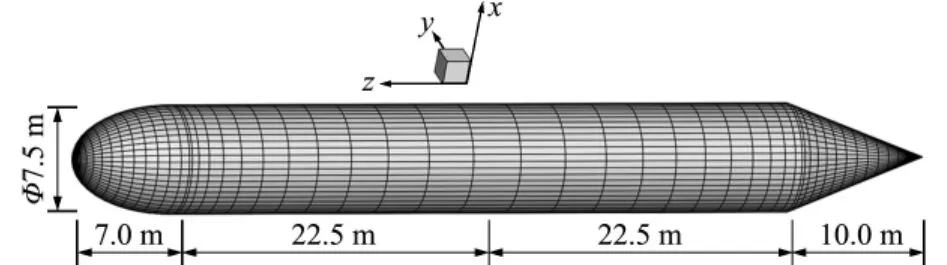
图8 NURBS构建的简化BeTSSi模型Fig.8 Simple BeTSSi model built by NURBS
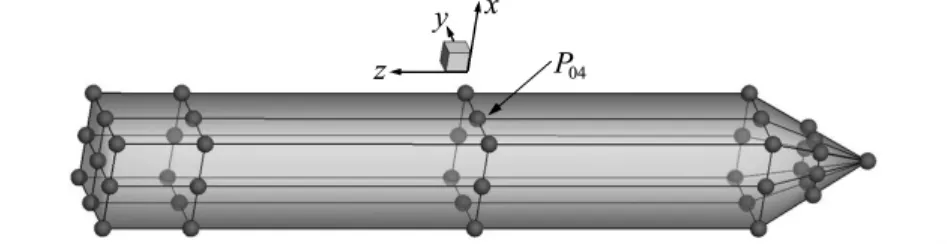
图9 简化BeTSSi的NURBS控制点信息Fig.9 NURBS control points of the simple BeTSSi
考虑入射波为平面波,沿y轴正向入射,幅值为1.0Pa,水中声速1524.0m/s。为了验证本文算法对大尺度壳体声散射仿真的正确性与有效性,首先用常量三角形单元离散该模型,形成103124个单元,将该方法得到的计算数值作为参考解。图10给出了本文算法计算点声压相对于参考解的误差,计算点等间距分布于xoy平面内距离艇轴心点6.0m的圆上。图10横坐标为计算点的极坐标角度,分析频率为100Hz。可以看出,随着自由度的增加,常量三角形单元边界元相对误差逐渐减小并趋于稳定,因此取103124个单元时的解作为参考解是可行的。本文算法在自由度相对较少的情况下,取得了与常量三角形单元边界元一致的计算精度,如本文算法881自由度与常量三角形单元5418自由度时的相对误差较为接近。针对大尺度壳体的声散射问题,本文算法利用NURBS建模,几何信息精确,因此离散规模远小于常量三角形单元的规模。

图10 等几何边界元法相比常量三角形边界元法的相对计算误差Fig.10 Relative error of IGA BEM simulations relative to constant triangle BEM
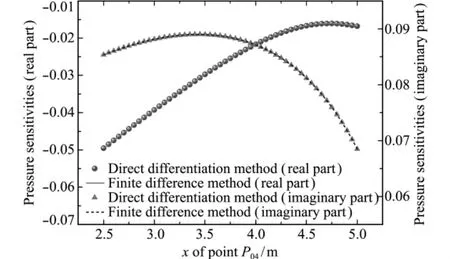
图11 点(6,0,0)处的声压敏感度值随控制点P04的x坐标变化关系Fig.11 Pressure sensitivities at point(6,0,0)with respect to the xcoordinate of P04
设计变量取图9中P04控制点的x坐标,分析频率为100Hz,计算自由度为315。图11给出了点(6,0,0)处的声压敏感度随设计变量的变化关系,有限差分法步长为0.001m,设计变量取值为2.5m~5.0m。可以看出,本文用直接微分法计算的结果与有限差分法的结果吻合良好,说明本文敏感度算法同样适用于大尺度模型。随着结构形状的变化,计算点声压敏感度呈现出不同的取值,这样的梯度信息可以为结构形状优化提供设计方向。图12和图13分别展示了xoy平面内目标区布情况,目标区域为20×20m的正方形。图12目标区域的声压模值分布表明艇身入射面声压较强,达到1.6Pa,而背面声压可降至0.4Pa。图13表明控制点的影响区域是有限的,离控制点越近,声压对控制点变化越敏感,因此基于本文算法的后续形状优化设计必须考虑控制点的布局。
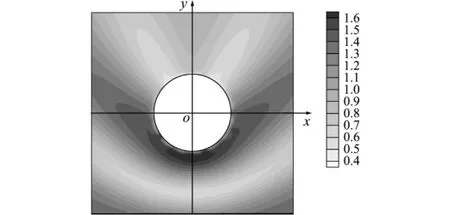
图12 目标区域声压模值分布(Pa)Fig.12 Distribution of sound pressure modulus on the reference surface
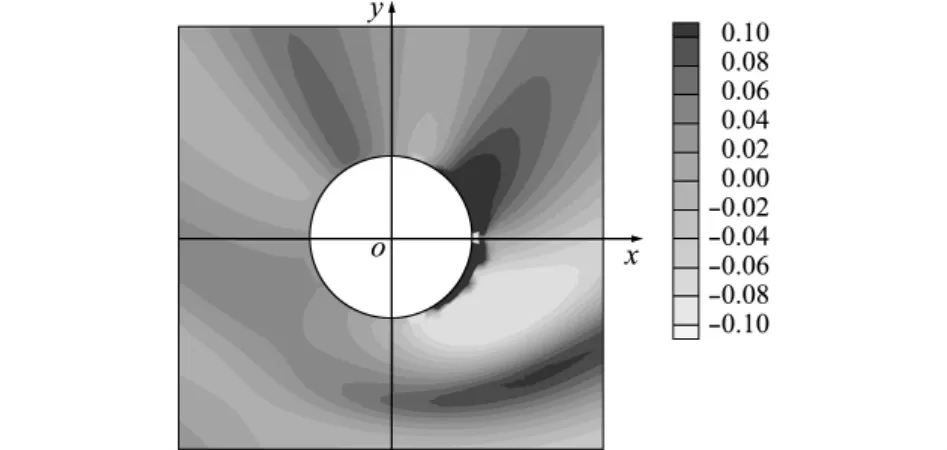
图13 目标区域声压敏感度值分布Fig.13 Distribution of sound pressure sensitivities on the reference surface
6 结 论
本文推导了基于NURBS基函数插值的三维声场等几何边界积分方程及其敏感度边界积分方程,针对边界积分方程中的奇异性,结合Cauchy主值积分和Hadamard有限部分积分,成功运用奇异相消技术给出超奇异积分的直接计算公式,并据此编写了计算程序。采用脉动球辐射算例和水下大尺度壳体的声散射问题,验证了本文算法和程序的正确性与有效性,并且基于脉动球给出其他不同形状的结构,初步考察了结构形状对声场声压分布的影响,为下一阶段结构形状优化工作做了理论准备。
