包含正圈的复符号非异性极小禁用圈链
2018-11-05陈淑梅
陈淑梅, 刘 月
(福州大学数学与计算机科学学院,福建 福州 350116)
0 引言
设z=a+ib是一个复数,其中a和b都是实数. 它的复符号,记作csgn(z),定义为
csgn(z)=sgn(a)+i·sgn(b)
其中: sgn(x)=1, -1或0分别对应于x>0,x<0或x=0. 一个复矩阵A的复符号模式,记作csgn(A),是把A中的每一个元素用相应的复符号替换后所得的矩阵. 与A具有相同复符号模式矩阵全体所构成的矩阵类称为A的复符号模式矩阵类,记作QC(A),即
QC(A)={B|csgn(B)=csgn(A)}
一个复矩阵称为复符号非异矩阵(简称CNS矩阵),若此矩阵的复符号模式可以保证矩阵是非奇异的,即QC(A)中所有矩阵均为非奇异.
复符号模式是符号模式(见文献[1])的一种复推广,由Eschenbach 等人在文献[2]中引入. 文献[3]定义了复符号模式矩阵的分裂变换. 利用分裂变换,在研究矩阵的复符号非异性时,可以局限在只含有{0, ±1, ±i}这五种元素的复符号模式矩阵中讨论. 若矩阵A的复符号模式csgn(A)中只含有{0, ±1, ±i}这五种元素,则称A为轴元阵. 本研究只讨论轴元阵.
除复符号模式推广外,还有一种复推广,称为ray模式推广(见文献[4]). 在ray模式推广中,非零复数z的ray定义为z/|z|,类似可以定义矩阵的ray模式ray(A)及ray模式矩阵类QR(A). 若A是轴元阵,根据定义易知ray(A)=csgn(A)且QR(A)=QC(A). 据此,轴元阵可以认为是复符号模式和ray模式的“交”.
复符号非异矩阵是符号非异矩阵(即SNS矩阵)的复推广,其中SNS矩阵是符号可解性理论中的核心研究对象(见文献[5]). 在ray模式推广下,相应的SNS矩阵的推广为ray非异矩阵(简称RNS矩阵). 由轴元矩阵的特殊性,当矩阵A是轴元阵时,A是CNS矩阵等价于A是RNS矩阵. 于是,关于RNS矩阵的所有结论在讨论轴元矩阵的CNS性时均可使用.
文献[6]中定义了一类结构简单的完全不可分矩阵,称为圈链矩阵. 该文同时利用一个特殊集合函数Φn(Θ)把圈链矩阵分为三类,分别为RNS圈链矩阵、反常圈链矩阵和禁用圈链矩阵. 文献[7]中证明了禁用圈链矩阵也是一般ray非异矩阵的禁用结构. 相应地,轴元禁用圈链矩阵也是CNS矩阵的禁用结构.
文献[8]中给出了不含正圈时Φn(Θ)的计算公式,利用此公式可以较为直观地识别禁用圈链矩阵,即可认为在没有正圈时,禁用圈链矩阵的识别问题已经完全解决. 本研究给出圈链轴元阵中两端都是正圈的极小禁用圈链的特征刻画,此特征刻画中没有使用Φn(Θ),从而也可较为直观地识别此类矩阵.
1 预备知识
本节给出圈链矩阵的一些相关定义及基本性质.
接下来主要关注形如M=I-A(W)的矩阵M,其中W是一个简单赋权有向图(不含环及重弧),A(W)是W的邻接矩阵.
设W是一个简单有向图,记C=C(W)={C1,C2, …,Cn}为W中所有有向圈所构成的集合.W的圈图,记作CG(W),定义为顶点集为C、弧集合为E的无向图,其中CjCk∈E当且仅当Cj和Ck在W中有公共点.
定义1若简单赋权有向图W的圈图CG(W)是一条路,则称W为圈链图. 设W是圈链图,则称矩阵M=M(W)=I-A(W)为圈链矩阵.
记M0是空矩阵,且对于1≤j≤n,设Mj是C的主子圈链Cj={C1,C2, …,Cj}对应的圈链矩阵,则称M0,M1, …,Mn为M的顺序子圈链矩阵. 记-ω(Cj)=ωj=rj·eiθj,其中rj=|ωj|是复数ωj的模,eiθj=-ray(Cj),-π<θj≤π,j=1, 2, …,n. 文献[6]中给出了如下的递推公式:
detMj=rj·eiθj·detMj-2+detMj-1(j=2, …,n)
(1)

记
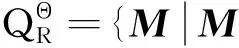
文献[6]中给出了如下的定义:


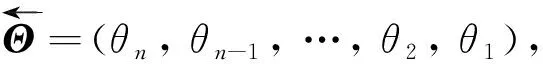
设序列Θ不是复符号非异的. 若任意一个包含Θ作为子序列的序列都不是复符号非异的,则称Θ为禁用序列; 否则称Θ为反常序列. 根据定义,只需要刻画极小禁用序列.
文献[6]中证明了任意序列包含一个禁用序列作为子序列也是禁用序列. 圈链矩阵不是复符号非异的也可以分成两类: 若圈链的辐角序列是反常序列则称该圈链为反常圈链; 若圈链的辐角序列是禁用序列则称该圈链为禁用圈链. 因此,任意圈链包含一个禁用圈链作为子圈链也是禁用圈链.
接下来给出圈链的一些基本性质.
性质1设Θ=(θ1,θ2, …,θn). 则
1)Θ是禁用序列当且仅当Φn(Θ)=(-π, π][6].
2)Θ是反常序列当且仅当Φn(Θ)是{0, π},[0, π]或[-π, 0]中的一个[7].
3)Φn(Θ)={0}当且仅当任意一个j=1, 2, …,n,θj=0.
4)Φn(Θ)={0, π}当且仅当θj∈{0, π},其中j=1, 2, …,n且至少存在一个j使得θj=π.

6) 若θ1=0,则Φj-1(Θ2, j)=Φj(Θ).
7) 设θj=0. 若π∈Φj-1(Θ)或π∉Φj-2(Θ),则Φj(Θ)=-Φj-1(Θ)≜{-φ|φ∈Φj-1(Θ)}[6].
由上述性质1中 6)可知,不妨假设本研究中的Θ两端都不是0.
下面的引理刻画了反常序列.
引理1[6]设Θ=(θ1,θ2, …,θn),其中-π<θj≤π,且k1 1)θks+1=θks或者θks+1=Arg(-ei·θks),s=1, 2, …,p; 2)θj∈{0, π}其中ks+1 3) 设ts是θks和θks+1之间零元素的个数,若ts是偶数, 则θks+1·θks+1>0; 若ts是奇数,则 θks+1·θks+1<0 (s=1, 2, …p-1) 在文献[7]中,已经证明了圈链矩阵M(不一定是圈链矩阵)是一般RNS矩阵的禁用结构当且仅当M是禁用圈链矩阵,它表明了禁用圈链矩阵在RNS性质研究中的重要性. 虽然上述的性质1中1)提供了一个判断Θ是否是禁用序列的工具,但是它并不直观. 在研究中将给出一个更加直观的刻画并且避免使用Φj(Θ). 文献[6]中给出了如下的计算公式: (2) 其中 记arg(ei·(θj-θ))=ϑ,则 (3) 根据公式(2)~(3),可以计算出Φj(Θ){0, π}=(a, 0)∪(0,b),其中-π≤a≤0,0≤b≤π. 在接下来的证明中,一些计算也是基于这两个公式的. 引理2设Θ=(θ1,θ2, …,θn)满足θ1,θn≠0. 若Φn(Θ)=(a-π, 0)∪(0,a),其中0 证明 由公式(2)~(3)知,π∉Φn-2(Θ)且Φn-1(Θ){0, π}=(a1, 0)∪(0,b1),其中-π≤a1≤0,0≤b1≤π. 若π∉Φn-1(Θ),则Φn-1(Θ){0}=(a1, 0)∪(0,b1). 由于θn≠0,则由公式(2)~(3)知,Φn(Θ)≠(a-π, 0)∪(0,a),矛盾. 因此π∈Φn-1(Θ). 由性质1中1)~2)知,Φn-1(Θ)={0, π}, [0, π], [-π, 0]或(-π, π]. 若Φn-1(Θ)=[0, π], [-π, 0]或(-π, π],则通过计算,可得Φn(Θ)≠(a-π, 0)∪(0,a),矛盾. 从而Φn-1(Θ)= {0, π}. 由性质1的4)知,θj∈{0, π},j=1, 2, …,n-1且至少存在一个j使得θj=π. 因为θ1≠0,所以θ1=π. 又因为π∉Φn-2(Θ),所以n=2. 证毕. 证明 因为Θ是极小禁用序列,所以θ1≠0. 又因为Θm是反常序列且θm≠0,所以由引理1知,θ1=θm=π. 下证Θm=(π, 0, …, 0, π). 用反证法,假设Θm≠(π, 0, …, 0, π),则分如下两种情形. 情形1:θj∈{0, π}其中1 通过计算得Φm(Θ)={0, π}. 不妨设θl=π是离θm最近的π,即对任意的j(l Φn-l+1(Θl, n)=Φn(Θ) 从而Θl, n是禁用序列,这与Θ是极小矛盾. 情形2: 存在1 不妨设θj′∉{0, π},当j′ Φm-j′+1(Θj′, n)=Φm(Θ){0, π}=(0, π)或(-π, 0) 因Θ是禁用序列, 故由引理1知,存在m Φj″-j′+1(Θj′, n)=Φj″(Θ){0, π} 从而 Φj0-j′(Θj′, n)=Φj0-1(Θ){0, π} 故由公式(2)~(3)知, Φj0-j′+1(Θj′, n)=Φj0(Θ) 若Φj0-1(Θ){0, π}=(-π, 0),则Φj0(Θ)=(-π, π],从而Φj0-j′+1(Θj′, n)=(-π, π]. 由性质1中 1)知,Θj′, n是禁用序列,与Θ是极小矛盾. Φj1-j′+1(Θj′, n)=Φj1(Θ) 从而Θj′, n是禁用序列,与Θ是极小矛盾. 故Θm=(π, 0, …, 0, π). 容易验证θm+1∉{0, π}. 若不然,设θm+1∈{0, π}. 令Θm, n=(θm,θm+1, …,θn),则 Φn-m+1(Θm, n)=Φn(Θ) 2) 若存在j(1 由性质1 中7)知, 1) 若存在j(1 2) 设h1 证明 必要性: 先证结论1). 下面根据θ2的取值把证明分成如下三种情形: 情形1:θ2=π. 此时可得θ3∉{0, π}. 若不然,可设θ3∈{0, π}. 令Θ2, n=(θ2,θ3, …,θn),则 Φn-1(Θ2, n)=Φn(Θ) 情形2:θ2=0. 设Θj0=(θ1,θ2, …,θj0), 下证θ3, …,θj0-1=0. 用反证法,假设θ3, …,θj0-1不全为0,则设θj′是离θj0最近的一个不为0的元素,其中3≤j′≤j0-1. 因为Θ是极小禁用序列,由引理3知,Θj0不是反常序列. 并且Θj0也不是禁用序列,故Θj0是复符号非异的. 因为θ1=θj0=π且不存在1 Φj0-1(Θ2, n)=Φj0(Θ) 从而 Φn-1(Θ2, n)=Φn(Θ) 故Θ2, n是禁用序列,与Θ是极小矛盾. 因此Θj0=(π, 0, …, 0, π). 由引理1知,Θj0是反常序列. 由于θj0≠0,根据引理3知,Θ=(π, 0, …, 0, π,φ, π),其中φ∉{0, π}. 情形3:θ2∉{0, π}. 综合上述所有情形,可知结论1)成立. 下证结论2). 将证明分成如下两种情形: 情形①:k=1. 情形②:k≠1. 因为Θ是极小禁用序列且θ1=π,则由引理4中的2)知,θh2j+1=(-1)t2jθh2j,即 θh3=(-1)t2θh2,θh5=(-1)t4θh4, …,θhk=(-1)tk-1θhk-1 θh2=(-1)t1θh1,θh4=(-1)t3θh3, …,θhk-1=(-1)tk-2θhk-2 故θhj+1=(-1)tjθhj. 因此,结论2)成立. 必要性得证. 充分性: 由已知条件及公式(2)~(3)知,通过计算容易验证Φn(Θ)=(-π, π]. 由性质1中1)知,Θ是禁用序列. 同样地,容易验证Θ的任意一个子序列都不是禁用序列,因此Θ是极小禁用序列. 充分性得证. 证毕.2 一些特殊的圈链及其Φn(Θ)

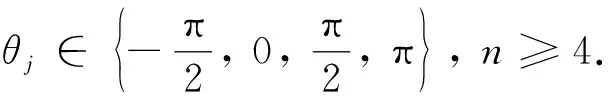
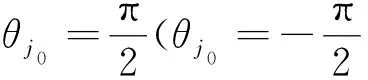


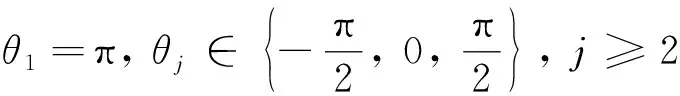


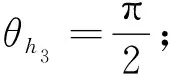

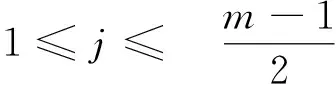


3 主要结果