基于Amesim的直动式溢流阀动态特性分析

张 磊，付娟娟，陈 帆，杨 帆

(武汉软件工程职业学院 机械工程学院，湖北 武汉 430205)

0 引 言

溢流阀是液压系统中必不可少的压力控制元件，其主要作用是控制和维持液压系统中的压力恒定，使其不超过溢流阀的调定压力，以保护液压回路的工作安全。溢流阀按结构和工作原理可分为直动式溢流阀和先导式溢流阀，与先导式溢流阀相比，直动式溢流阀具有结构简单(一级阀)、灵敏度高、稳压性能好等优点，故常作为安全阀和限压阀应用于低压小流量液压系统中。

直动式溢流阀性能的优劣对整个液压系统的工作稳定及运行安全有着重要的影响。通过建立直动式溢流阀的动态数学模型，使用Amesim软件分析直动式溢流阀各结构参数对其动态特性的影响，可为直动溢流阀的优化设计与性能评价提供理论依据。

1 建立模型

1.1 工作原理

如图1所示为直动式溢流阀结构和职能符号[1]。液压泵输出的液压油流经进油口P和阻尼孔5之后作用在阀芯4底部，并产生一个向上的作用力p1。当p1小于调压弹簧3的调定压力时，阀芯4不动，P、T口不通；反之，阀芯4上移，封闭的出油口T打开，液压油经出油口T流回油箱。随着液压油的溢流，进油口压力也随之下降，作用在阀芯上的力p1也随之减小；当p1下降到弹簧的调定压力时，阀芯处于平衡状态。由于液压油经过阻尼孔有压力损失，故p1总是小于进油压力p。

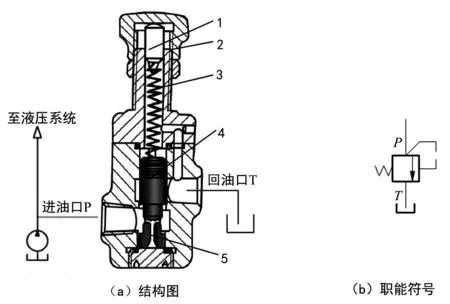
图1 直动式溢流阀结构和职能符号1.调节杆 2.调压螺母 3.调压弹簧 4.阀芯 5.阻尼孔

1.2 动态特性分析

直动式溢流阀的动态特性是指阀芯在接到输入信号后，从初始状态到稳定状态的响应过程，常用压力和时间两者的关系(时间特性)来描述[1-2]。直动式溢流阀动态性能指标主要包括：压力超调量、响应时间、过渡过程时间等。

1.2.1动态数学模型

直动式溢流阀工作过程受干扰因素较多，在建立数学模型时应充分考虑液压力、阀芯重力、质量惯性力、粘性摩擦力、弹簧力、稳态液动力、瞬态液动力等因素。将直动式溢流阀结构原理图转化成物理模型如图2所示。

图2 直动式溢流阀物理模型

建立动态数学模型为：

(1) 阀芯受力平衡方程

(1)

式中:p1为溢流阀的阀芯底部压力；A为阀芯下端面积；m为阀芯质量；m2为阀芯当量质量，等于阀芯质量加调压弹簧质量的1/3；x0为阀芯调压弹簧预压缩量；x为阀芯位移；fx为阀芯运动阻尼系数；Kex稳态液动力等效当量弹簧刚度；KLx为阀口瞬态液动力粘性阻尼系数。

(2) 阀芯阀口的流量连续方程

(2)

式中:qx为主阀溢流量；q1为阻尼孔流量；V为阀芯进口体积；E为油液弹性模量。

(3) 阀芯底端的流量连续方程

(3)

式中:V1为滑阀阀芯底端的体积。

(4) 溢流阀阀口流量

=Kqxx+Kcxp

(4)

式中:Cd为阀口流量系数；ρ为液压油的密度；Kqx为阀口流量增益；Kcx为阀口流量压力系数。

(5) 阻尼孔流量

qq=GR1(p-p1)

(5)

式中:GR1为阻尼孔的液导；p为主阀进口压力。

1.2.2构建传递函数方框图

(1) 方程的线性变化及拉普拉斯变换

将式(1)～(5)动态方程在某一稳态工作压力下进行线性化，并取拉普拉斯变换。

对式(1)进行拉普拉斯变换：

(6)

对式(2)～(5)进行拉普拉斯变换的：

(7)

(8)

(2) 传递函数方框图

根据式(1)中拉普拉斯变换得到的公式(6)～(8)画出传递函数方框图，可得直动式溢流阀“流量—压力”传递函数方框控制图如图3所示。

图3 直动式溢流阀流量-压力传递函数方框图

由图3易知：直动式溢流阀控制回路由两个惯性环节、一个比例环节、一个二阶振荡环节组成。

其中，回路的传递函数总增益为：

(9)

惯性环节的频率为：

(10)

二阶振荡环节频率为：

(11)

由上式(9)～(11)可知，弹簧刚度Kx、液动力刚度Kex、阀芯质量m、阀芯底端面积A、阻尼孔大小，都将影响阀芯的动态特性。

采用Amesim软件分析上述各因素对直动式溢流阀动态特性的影响，直观描述各因素对溢流阀动态特性影响的程度，为溢流阀的选择、设计和结构优化提供依据。

2 Amesim软件仿真分析

2.1 建立Amesim仿真模型

利用Amesim软件中HCD液压元件库和Mechanical机械元件库，根据图2所示的直动式溢流阀物理模型，建立其仿真模型[3-8]，如图4所示。

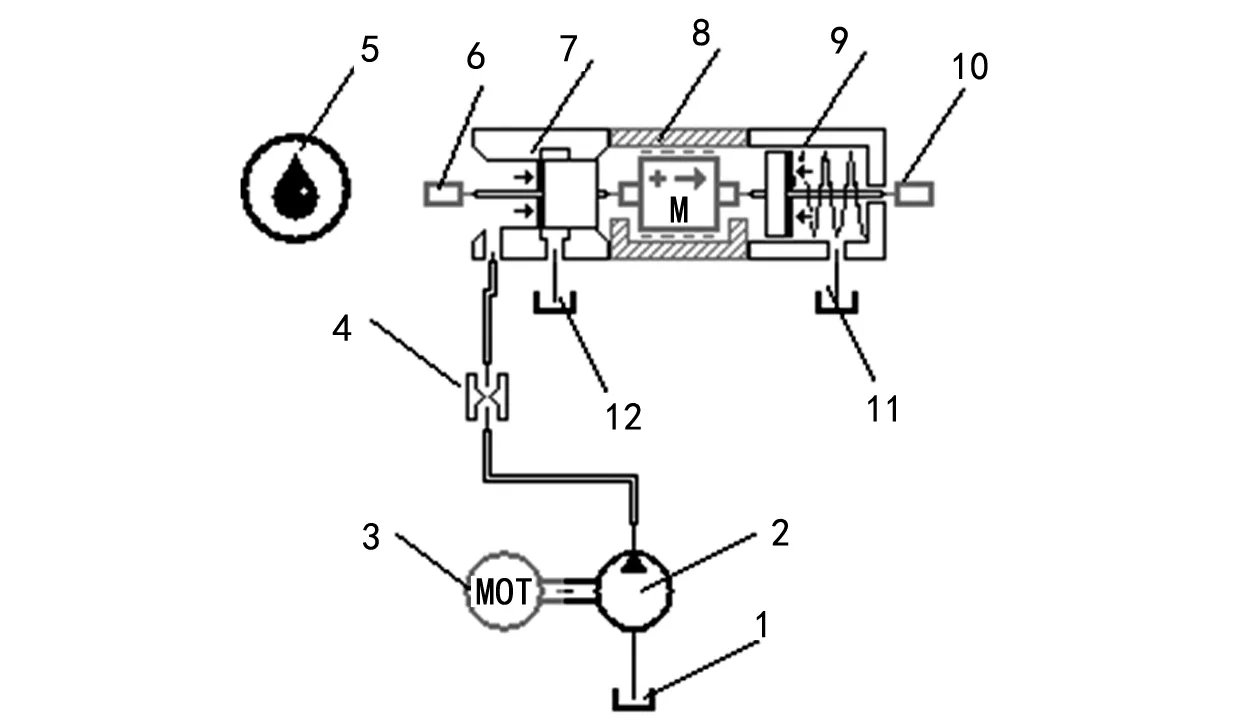
图4 直动式溢流阀Amesim仿真模型1、11、12.油箱 2.液压泵 3.电机 4.阻尼孔 5.液压属性 6、10.速度基准 7.阀芯模型 8.阀芯部件质量块 9.调节弹簧

2.2 仿真分析

2.2.1阻尼孔直径的影响

图5(a)是阻尼孔直径分别为3.5 mm、4.5 mm、5 mm时直动式溢流阀压力响应特性曲线。由图可知，阻尼孔直径越小，液压油所受阻力越大，阀的压力超调量越大，响应时间和过渡时间越长，振荡越严重。图5(b)是阻尼孔为0.000 1 mm时直动式溢流阀压力响应特性曲线。由图可知，当阻尼孔直径小到一定极限(阻尼孔堵死时)，溢流阀进油口的压力值产生冲击并迅速减小趋于稳定。因此，设计和选用直动式溢流阀时，适当增大阻尼孔直径可缩短直动式溢流阀的响应时间，提高其稳定性。

2.2.2阀芯质量的影响

图6(a)是阀芯质量分别为0.15 kg、0.2 kg、0.3 kg时直动式溢流阀压力响应特性曲线。由图可知，增大阀芯质量，响应时间减小，但压力超调量偏大，振荡剧烈，溢流阀压力达到稳定压力时间较长。图6(b)是阀芯质量分别为0.05 kg、0.1 kg时直动式溢流阀压力响应特性曲线。由图可知，当阀芯质量在较小范围内变化时，直动式溢流阀的动态特性几乎无变化。因此，设计和选用直动式溢流阀时，在允许范围内，阀芯质量尽量取小，可减小压力超调量和响应时间，提高其稳定性。

2.2.3滑阀直径的影响

由式(1)和图7可知，当滑阀直径为8 mm时，峰值压力达到46 MPa、过渡时间达到0.3 s，稳定压力为36 MPa；当滑阀直径为10 mm时，峰值压力达到30 MPa、过渡时间达到0.03 s，稳定压力为24 MPa；当滑阀直径为12 mm时，峰值压力达到20 MPa、过渡时间达到0.03 s，稳定压力为16 MPa。

通过比较可知滑阀直径越小(底端面积A、体积V1均随之减小)，溢流阀的稳定压力、压力超调量、过渡时间越大，振荡次数明显增加，稳定性越差。因此，设计溢流阀时，应根据液压系统工作压力要求，在合理范围内选择较大的滑阀直径值。

图7 不同的阀芯直径(底端面积、体积)时压力响应特性曲线

2.2.4弹簧刚度的影响

图8为不同的弹簧刚度时压力仿真曲线。

图8 不同的弹簧刚度时压力仿真曲线

图8(a)是弹簧刚度分别为80 N/mm、100 N/mm、120 N/mm时直动式溢流阀压力响应特性曲线。

由图可知，弹簧刚度越小，溢流阀进口的控制压力、压力超调量、过渡时间越短，振荡次数越少，稳定性较好。图8(b)是弹簧刚度为0 N/mm时溢流阀动态特性仿真曲线，由图可知，当弹簧过软，即弹簧刚度相当于0 N/mm时，溢流阀调节压力很小，相当于常开状态，液压泵直接经溢流阀卸荷，执行元件无法正常工作。因此，设计和选用直动式溢流阀时，应根据液压系统的工作压力，选择合适的弹簧刚度，既不能太硬也不能太软，太硬调节困难、太软容易造成系统压力上不去。

3 结 论

在建立直动式溢流阀的动态数学模型及Amesim仿真模型之后，通过动态数学模型及Amesim软件仿真直观地分析了阻尼孔大小、阀芯质量、滑阀底端面积、弹簧刚度等因素对直动式溢流阀动态特性响应的影响，即验证了所建模型的正确性，也为直动式溢流阀参数优化设计提供了参考。