基于谐响应分析的叶片裂纹故障诊断方法

牛宏伟,文 敏

(中国飞行试验研究院，陕西 西安 710089)

0 引 言

叶片作为航空发动机关键零件承担能量转换重任，工作环境恶劣、受载复杂，除受离心载荷、气动载荷及振动载荷外，亦受高温、腐蚀影响，疲劳断裂故障常见[1-2]。工作中出现裂纹不仅影响发动机性能，且高速脱离的断裂叶片对转子系统其它部件或机匣的安全造成严重威胁[3-4]。裂纹叶片的振动特性已逐渐成为一些学者的研究对象。裂纹萌生及扩展会会改变叶片原有振动特性，裂纹的存在会使叶片刚度减小，从而改变叶片固有频率和振型[5]。由于固有频率对裂纹深度的改变并不敏感，据此进行叶片裂纹诊断的精度有限，因此需寻求其他方法来表征裂纹叶片的振动特性变化。其中谐响应分析就是一种方法，目前研究裂纹叶片主要采用悬臂梁法，而真实叶片由于带扭转和截面变化，与悬臂梁假设有所出入[6]。采用有限元法分别建立无裂纹叶片和不同裂纹参数叶片模型，分别利用模态分析和谐响应分析研究裂纹叶片的固有振动特性和受迫振动响应，通过与无裂纹叶片振动特性进行对比，可实现对裂纹叶片的诊断识别。

1 叶片数值分析模型

将叶片离散为梁单元，无裂纹叶片的振动方程为：

[M]e{q(t)}e+[K]e{q(t)}e={F(t)}e

(1)

式中：[M]e为单元质量矩阵；[K]e为单元刚度矩阵；{F(t)}e为单元的外部施加力矢量；{q(t)}e为单元的节点响应。假定裂纹只影响叶片的刚度而不影响质量，则裂纹叶片的振动方程为：

[M]e{qc(t)}e+[Kc]e{qc(t)}e={F(t)}e

(2)

式中：{qc(t)}e为裂纹单元的节点响应，[Kc]e为裂纹单元刚度矩阵。

[Kc]e=[T][C](e)-1[T]

(3)

[C]e=[C0](e)+[Cc](e)

(4)

式中：[C0](e)为无裂纹叶片的单元动柔度矩阵，[Cc](e)为裂纹单元动柔度矩阵；[C]e为含有裂纹叶片的总动柔度。

将上述矩阵进行组装可得到叶片总振动微分方程：

[M]{q(t)}+[K]{q(t)}={F(t)}

(5)

式中：[M]、[K]、{F(t)}分别为组装后的质量矩阵、刚度矩阵和外力矢量矩阵。

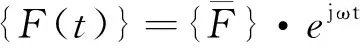
(6)

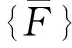
(7)

(8)

给定边界条件，[M]和[K]以及激振力幅值，即可计算出单元的谐响应值。

对某型发动机宽弦风扇叶片三维模型进行了适当简化，得到用于分析的模型，叶高495 mm，叶根弦长150 mm，叶片材料为TC4钛合金，杨氏模量E=109 GPa，泊松比ν=0.34，密度ρ=4 440 kg/m3。采用SOLID45单元对叶片进行网格划分，并在叶片上添加裂纹，见图1。

图1 裂纹叶片网格模型

2 裂纹叶片动力学分析

2.1 固有振动特性

描述裂纹参数的量主要有裂纹位置和裂纹深度，笔者用裂纹距离叶根的相对高度来表征裂纹位置，即Hc=h/H，h为裂纹距叶根距离，H为叶高；用裂纹长度与叶根弦长的比值来表征裂纹深度，即Lc=l/L，l为裂纹深度，L为叶根弦长，Hc和Lc均为无量纲量，表1为计算状态矩阵，分别考虑了不同裂纹位置和不同深度的情况，Lc=0代表没有裂纹。

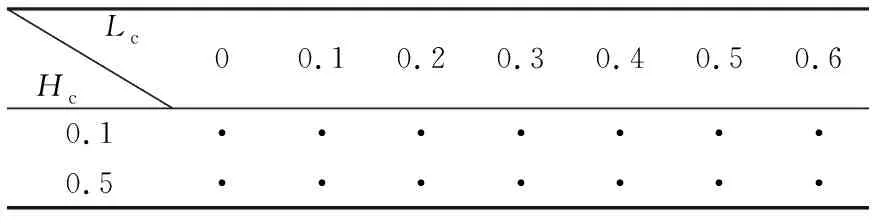
表1 模态分析计算条件矩阵

首先进行模态分析，图2显示了叶片产生裂纹后的一阶弯曲固有频率变化，对频率作了无量钢化处理，以无裂纹叶片的频率作为1。

图2 裂纹深度及位置与一阶弯曲固有频率关系曲线

从图中可以看出，随着裂纹深度的增加，叶片一阶弯曲固有频率逐渐降低，深度相同时，裂纹离叶根固定端越近，对固有频率的影响越大。当Hc=0.1，Lc=0.6时，叶片一阶弯曲固有频率下降了15.2%，裂纹对于叶片刚度的衰减效应已十分明显。

2.2 谐响应分析

在叶片上施加不同方向的力会激起不同的振型，例如若施加轴向力，会出现弯曲振型，而若施加叶高方向的力，可能激起扭转振型。根据前期技术小结的分析结果，叶片气动力对固有频率影响很小，因此对叶片施加离心力和交变气动力，求解不同裂纹参数叶片的谐响应，给定频率范围为0～800 Hz。

图3为无裂纹叶片的全范围频谱，存在多个响应峰值，分别对应结构的1、2、4阶固有振型，施加了转速后，存在明显的应力刚化效应，各阶固有频率显著增大。

图3 无裂纹叶片全范围响应频谱

图4为Hc=0.1在处添加不同深度裂纹后，150～180 Hz范围内叶尖轴向位移的响应频谱。相比于对固有频率的影响，裂纹深度的变化对谐响应幅值的影响更大，从无裂纹到Lc=0.15，第2阶频率仅减小了1.2%，但振动位移幅值却增加了80.1%。

接下来讨论裂纹高度对于谐响应的影响，固定裂纹深度Lc=0.1，Hc分别取0.1，0.5，0.8，在150～180 Hz响应频谱见图5，可以看出在固定裂纹深度的情况下，裂纹位置对结果影响不大，三个位置最大与最小响应峰值仅相差3.4%。

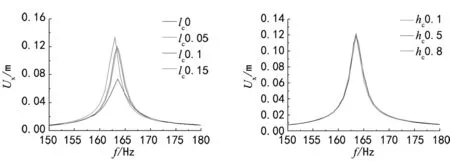
图4 Hc=0.1不同裂纹深图5 Lc=0.1不同裂纹高 度150～180 Hz响应频谱 度150～180 Hz响应频谱

裂纹的存在对于应力分布也有很大影响，图6为无裂纹叶片和Hc=0.1，Lc=0.1叶片Von Mises等效应力分布的对比，可以发现由于裂纹的产生，使叶片的局部应力分布发生了变化，在裂纹尖端存在明显的应力集中。无裂纹叶片的应力峰值出现在叶根部位，为632 MPa，而裂纹尖端应力峰值达到了703 MPa。

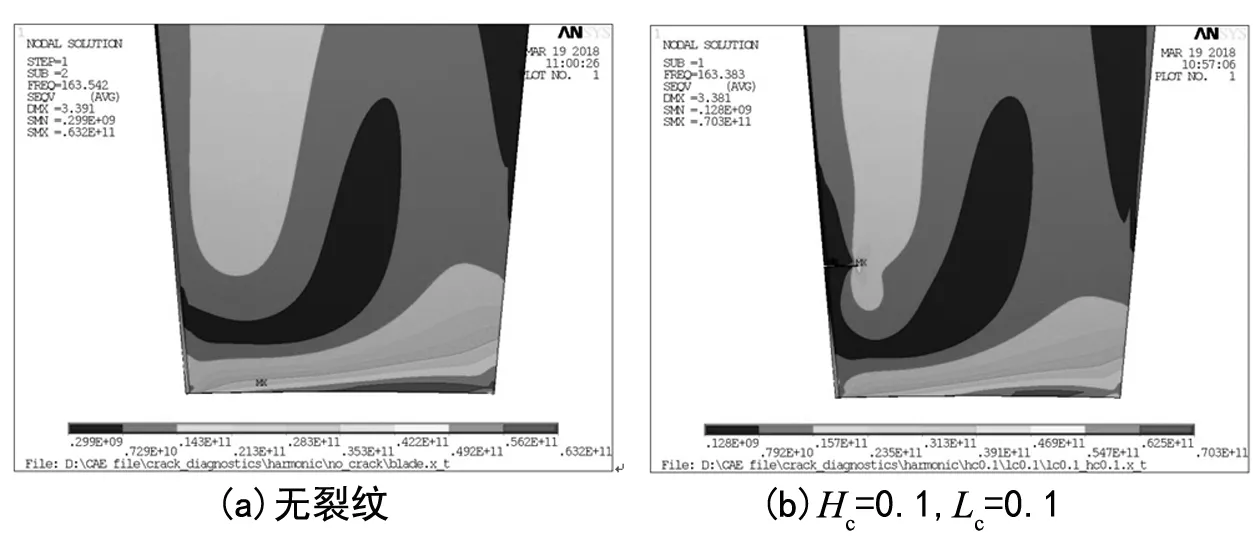
图6 裂纹引起的叶片应力重新分布

3 裂纹诊断方法

根据上述分析结果，裂纹叶片相比于无裂纹叶片谐响应幅值和固有频率都会产生一定变化，利用这一特性，结合叶尖振动测量系统，配合一定的处理算法，就可对裂纹叶片实现在线诊断。

与传统的接触式振动测量方法相比，非接触方法有很多优势，其中又以叶尖定时法应用较为广泛[7]。叶尖定时法的基本原理是将传感器沿径向安装在相对静止的机匣上，利用传感器感受在其前面通过的旋转叶片所产生的脉冲信号，以此来记录叶片到来的时刻。由于叶片的振动，叶片的端部相对于转动方向将会前移或者后移，即叶片脉冲到达时间t会随着叶片的振动发生改变，通过一定算法对该时间信号序列进行处理，可获得叶片振动参数的信息。其基本原理见图7。

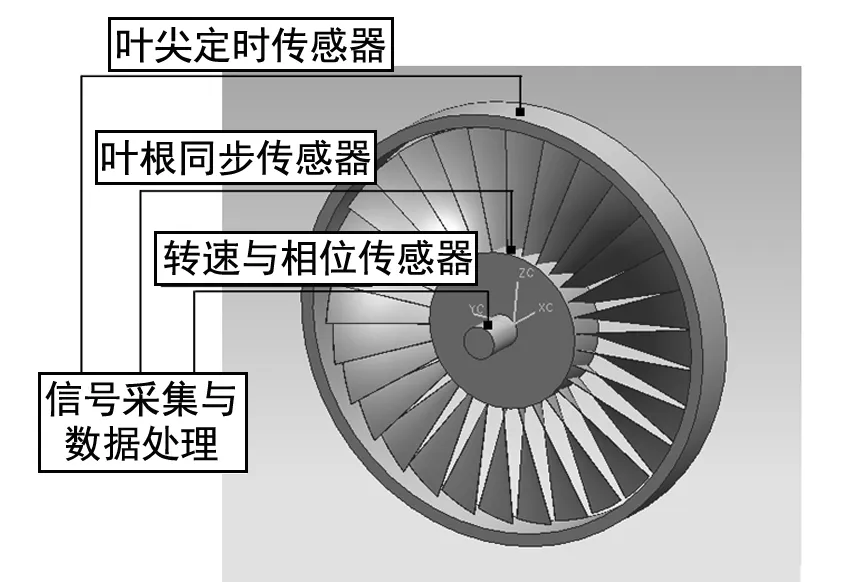
图7 基于叶尖定时原理的旋转叶片测振系统

采集得到叶尖位移数据后，将数据流输入故障诊断算法程序，算法流程如图8所示，其中M为叶片数量。一旦其中某个叶片因裂纹出现使叶片抵抗变形的刚度减小时，叶尖的位移响应峰值较同排其它叶片要大得多，据此可以诊断裂纹的出现[8]。另外结合相位传感器信号可具体定位到该叶片。δ为判定叶片位移峰值异常的阈值，需要通过进一步数值分析或试验确定。

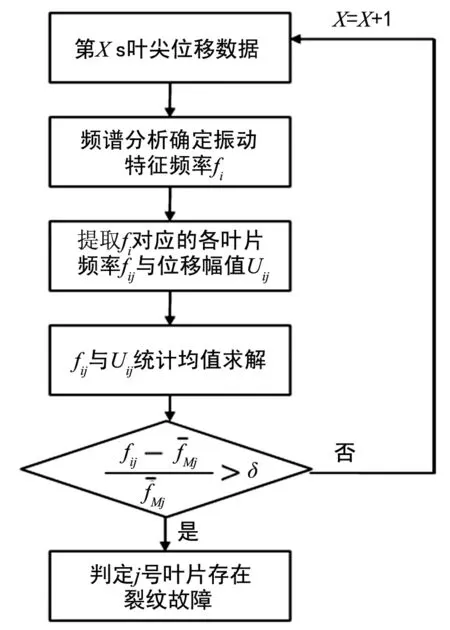
图8 裂纹叶片诊断算法流程

4 结 论

分别利用模态分析法和谐响应分析法研究了带裂纹叶片的固有振动特性和受迫振动特性，结果表明在不旋转状态裂纹会使叶片固有频率减小，而在旋转状态下，裂纹的存在对叶片固有频率的影响相对较小，但对谐响应幅值的影响较大。叶尖位移幅值随着裂纹深度的增加而显著增加，同时对裂纹产生的位置并不敏感。基于这一特性，可以通过非接触手段测量叶尖位移，配合一定算法，有效识别出裂纹叶片在特征频率下叶尖位移与正常叶片的区别，从而实现对叶片裂纹故障的在线诊断。