Win Ratio法在比较两组间非正态分布数据中的应用

李 超 康轶君 朱 妮 Tao Chen Duolao Wang△ 颜 虹△

【提 要】 目的 介绍Win Ratio法的原理及技术,以及此方法在比较两组间非正态分布数据中的应用。 方法 以一项随机对照双盲试验为例,采用Win Ratio法比较不符合正态分布的结局变量(孕周)在两组间的差异,并利用Bootstrap法估算相应的置信区间。同时比较与传统非参数检验方法结果之间的差异,所有分析均采用SAS 9.4软件。 结果 Win Ratio法估算干预组孕周高于对照组的概率为52.83%,置信区间为(1.04,1.21)。该结果与传统非参数方法一致,但Hodges& Lehmann法估计的置信区间结果中包含0。结论 相比传统非参数检验方法,Win Ratio除能够在区间估计的基础上判断组间差异是否具有统计学意义,还可以估计干预效应，同时可保证良好的可靠性和把握度。

在随机对照试验中经常会遇到结局变量为非正态分布的情况。当需要对两组间的结局变量进行比较时,目前最常用的方法是Mann-Whitney 检验,该方法能够对两组符合同一分布特征的结局变量进行分析并计算P值,从而直观地回答两组间的结局变量是否存在统计学差异,但该方法并不能检验干预的效应(干预组与对照组间差异的程度)[1-3]。为此,Hodges和Lehmann(HL)建议采用两组人群中的Shift参数以及其置信区间评价两组间相关结局变量的差异程度。然而该方法计算得出的Shift参数并不能直观地解释两组间的差别,同时当Mann-Whitney(MW)检验计算出的P值小于0.05时,该方法计算出的置信区间经常包含0[4-5]。为此,本文中介绍的Win Ratio法可以解决上述方法存在的问题。不仅可以评价干预效应,还可通过Bootstrap法估算干预效应的95%置信区间。由于目前国内尚无Win Ratio法的报道，因此希望通过本文的介绍能够让更多的科研工作者了解Win Ratio法,同时将该方法运用到实际工作中。

原理与方法

1.Win Ratio法的应用

Win Ratio法主要以每组被称为“Winner”和“Loser”的频数为基础进行推论的。在随机对照实验中所谓Winners为两组间研究对象所有可能的配对中,干预组结局变量数值大于对照组或干预效果好于对照组的例数,而干预组中数值较小或干预效果较差的例数则为Losers,干预组与对照组间数值相同或干预效果相同则称为“Tied”[6]。为便于理解,以一项临床试验为例进行说明,假设干预组A的频数为NA,对照组B的频数为NB,结局变量为美国纽约心脏协会定义的心功能分级,该变量是赋值为1～4的有序分类变量,1代表非常健康,4代表非常不健康[7]。假设干预组中i病人与对照组中j病人配成对,i病人的心功能分级为3,j病人为4。该种情况干预组中i病人称为Winner,j病人则称为Loser。Winners则为所有可能的配对中干预组A优于对照组B的例数(NW),Losers则为干预组A中劣于对照组B中的例数(NL),Tied为两组间所有可能的配对中相等的例数(NT)。其中干预组和对照组所有可能的配对数为NA×NB,且NW+NL+NT=NA×NB。

Win Ratio法采用指标RW=NW/NL来评价干预效应,即干预组和对照组间差异的程度。RW作为评价干预效应的指标也很好理解和解释。如果RW>1则说明结局变量的干预效果好于对照组。假设RW=2则说明在所有可能的配对中,干预组干预效果更优的概率是66.67% [RW/(RW+1)]。

2.Win Ratio法的统计推断

Win Ratio法在应用中的检验假设H0:RW=1,干预组与对照组间Winner的例数无差别;H1:RW≠1,干预组与对照组间Winner的例数有差别。本文中采用Bootstrap法估算RW的95%置信区间,如果95%置信区间包含1,则拒绝原假设,认为干预组与对照组间Winner的例数有差别[5]。

Bootstrap是基于原始数据观测值进行重复抽样,原始数据中每个观察对象每次被抽到的概率相等,且Bootstrap法要求重复抽样的次数应多于1000次[8-11]。对于每一次重复抽样的样本都可以计算出一个RW值,由于RW的分布情况取决于重复抽样的次数,且有之前的研究报道重复抽样样本计算出的RW属于偏态分布,因此本研究中在计算RW标准误时,对RW需先进行数据转换,取RW的对数值,使其满足正态分布后再求其相应的标准误,随后通过logRW的偏倚校正法求得logRW的95%置信区间[9,12]。最后据此求得RW的95%置信区间,当95%置信区间中不包含1时则拒绝原假设,认为两组间存在统计学差异。

3.Win Ratio的另一种区间估计方法

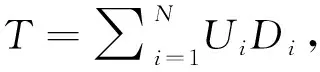
根据GGW法,我们可以通过相应步骤对RW的95%置信区间进行估算。首先对RW进行对数转换,logRW的标准误则由公式SE(logRW)=logRW/Z。随后logRW的95%置信区间则由公式logRW±1.96×SE(logRW)计算得出。最后据此求得RW的95%置信区间[6,13]。

实例分析

以2002年至2006年中国西部农村妇女孕期营养素补充干预试验(随机对照双盲试验)为例[14],2002年至2006年将孕妇随机分为叶酸组(1711人)和多微营养素组(1551人)。该研究项目主要的目的是评价不同营养素补充组间对出生体重的影响,因此出生体重作为该研究的主要目的。次要目的是比较孕周在不同营养素补充组间的差异。但通过正态性检验可知,结局变量孕周在两组间都不符合正态分布。叶酸组孕周的中位数为39.86周,多微营养素补充组中孕周的中位数为40.00周(表1)。

采用GGW,MW和HL方法比较两组间孕周的差别,结果发现两组间孕周差别具有统计学意义。且GGW和MW法给出的P值结果一致。HL法给出的Shift参数为0.1429,但该参数的95%置信区间包含0(表2)。

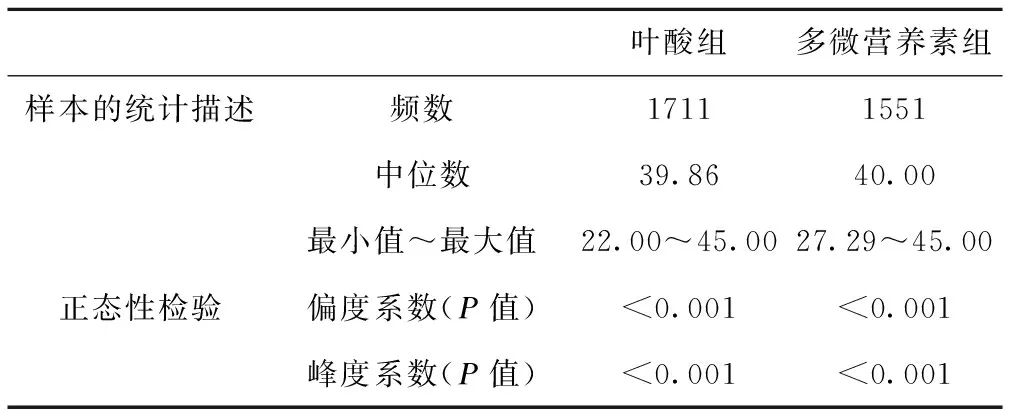
表1 两组间数据特征

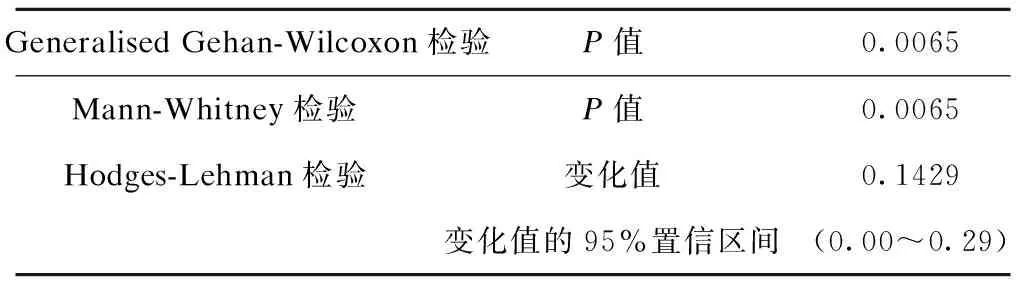
表2 传统非参数检验方法对两组间结局变量进行比较

表3给出了两组间所有可能的配对情况,共计2653761对,其中多微营养素组的Winners比例为51.50%,Losers比例为45.90%,Tied比例为2.60%。多微营养素补充组相比叶酸组的RW值为1.12,95%置信区间为(1.04,1.21)。因此认为两组间孕周的差异具有统计学意义,且多微营养素干预组孕周更高的概率为52.83% [RW/(RW+1)]。

表3 Win Ratio法对两组间结局变量进行比较

讨 论

传统的非参数检验方法如MW检验和GGW检验在比较两组间非正态分布的连续型变量时可以计算出P值,但是对评价干预效应即两组间结局变量的差异程度时则无能为力。HL法则可能通过计算Shift参数及Shift参数的95%置信区间来评价两组间的干预效应及差异是否具有统计学意义。但是该方法同样存在两点问题,首先,Shift参数不能很直观地反映干预效应,导致结果不易解释。其次,经常出现Shift参数95%置信区间包含0时MW和GGW检验的结果为P<0.05的情况[1-3]。本文实例分析部分中所举的中国西部农村妇女孕期营养素补充干预试验项目就存在类似的情况。在比较叶酸组和多微营养素补充组间孕周的差别时,HL法计算出的Shift参数95%置信区间包含0,然而GGW检验和MW检验所计算出的P值皆为0.0065。因此,该结果在一定程度上证实了HL法在估计两组间干预效应及差异是否具有统计学意义方面存在的问题。

本文中介绍的Win Ratio法能够很好地解决传统非参数检验方法中存在的问题。Win Ratio法不仅能够通过计算RW来直观的解释两组间的干预效应,同时通过Bootstrap法估算RW的95%置信区间,可以据此反映两组间的差异是否存在统计学意义。还有更为重要的一点是Win Ratio的原理也十分易于理解,从而利于更广泛的应用。不仅如此,之前的研究表明在保持一定的检验水准(犯Ⅰ类错误的概率)前提下,Win Ratio仍然有很好的把握度。同时该研究还指出,在比较两组间非正态分布的结局变量时,Win Ratio法的把握度与GGW检验和MW检验十分接近[6]。

即便Win Ratio法有着上述的优点，本文还需特别指出Win Ratio法在应用过程中的一些局限性。首先,Win Ratio法虽然可以采用分层的方式在一定程度上对相关因素进行校正,但是不能够在广泛的层面校正混杂因素对最终结果的干扰。其次,对于临床试验及许多科研项目中采用的重复测量设计,Win Ratio法不能对不同时间点间的区组效应进行估计,因此限制了Win Ratio法在此类设计数据中的应用。另外,目前尚无以Win Ratio法为基础的样本量估算公式应用于科研的实际工作。虽然Win Ratio法存在一定的局限性,但也为未来针对Win Ratio法的相关研究提供了发展方向。然而目前国内尚无公开发表的文章中报道使用Win Ratio法,也希望通过本文的介绍能够让让更多的科研工作者受益。有关Win Ratio法的应用,现已开发出相应的SAS程序,有兴趣使用该方法的科研工作者可以查询相应的参考文献或邮件联系本文作者。