从一道线性规划题的错解说起

广东省深圳市红岭教育集团高中部 马 锋

一、题目呈现

二、错解过程

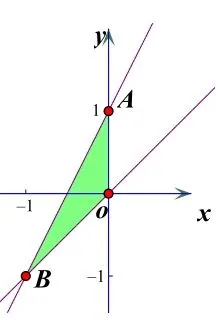
1.由题意画出可行域，如右图阴影所示。

2.将边界端点A（0，1）、B（-1，-1）的坐标代入m。

3.由于边界AB是虚线，结果应为开区间。

三、分析原因

四、解法剖析

解法一：分类讨论思想、转化思想

1.当x+y=0时，m=0。

（1）当xy=0时，m=1；

点评：此解法是纯粹的代数方法，主要是分类讨论思想，将目标函数恒等变形为关于斜率的“对勾”函数模型，结合反比例函数性质，最终解决问题。显然，此方法过程比较烦琐，运算量比较大，思维细节比较多，出错的风险自然很大，具有可操作性，但不易算对。

解法二：数形结合思想、转化思想、分类讨论思想

设直线l：x+y=0，过M作l的垂线，记垂足为N，连接OM，记OM的ON夹角为，则

1.当x+y=0时，m=0。

点评：这种解法主要是受到平面内两个距离公式（即两点间的距离公式和点到直线的距离公式）的启发，把目标函数恒等变形，转化为直角三角形中一个内角的正弦函数来处理。当然，里面也涉及了分类讨论思想，但相比解法一显然要简洁很多，主要是少了一层讨论，运算量明显减少，出错风险自然降低不少。

解法三：极坐标，坐标转化思想

点评：受目标函数形式的启发，结合极坐标直角坐标互化公式，直接转化为三角函数的值域问题，妙哉妙哉！此解法巧妙地回避了冗长的分类讨论，解法出其不意，运算量非常小，出错风险极低。

解法四：平面向量转化思想

点评：受目标函数分子和分母的启发，结合平面向量的数量积坐标运算，结合恒等变形处理，最终转化为向量的夹角问题，妙哉妙哉！此解法同样回避了冗长的分类讨论，解法新颖独特，运算量极低，想出错都很难！

五、反思小结

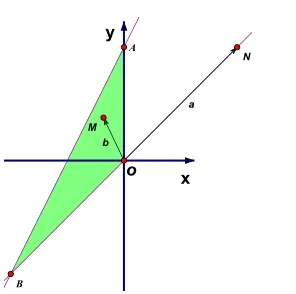
我们再来分析题目本身，求m的范围其实就是求m的两个最值，而本题最值的最优解其实有无穷多个，除端点A，B外，只要是可行域内边界直线x=0（最大值点）和y=x（最小值点）上的点都可以！因此本题采用代入法只会弄巧成拙。进一步思考：约束条件中第三条直线为什么没取等号呢？实际上，如果此处取了等号，这道题将毫无命题价值，没有任何检测意义，学生即便是投机代入，也可以得到最终的结果，这样将无法揭示学生的思维过程，根本没有诊断作用，对于教学来说，可以说是一道“费题”！可以料想，第三条边界直线设置成虚线其实是命题人故意设计的一个“陷阱”，由此我们不难看出命题人的良苦用心，为了暴露代入法的弊端，苦心设计一道这样的题目，已达到最终拯救“迷途”学生的目的，这个“套”下得真好，让我们为用心走心的命题人点赞喝彩！这也启示我们一线的教师，在命题选题时一定要有的放矢，题目务必有针对性和诊断性，以便更好地服务于教学工作。