基于挠度差值影响线的简支梁桥损伤识别研究

谢 雄

(西南科技大学 土木工程与建筑学院，四川 绵阳 621000)

1 引言

简支梁桥损伤识别主要是利用监测到的结构整体响应数据对简支梁桥结构损伤进行合理评判。近年来，国内各大中型城市为解决交通拥堵问题，修建了大量的城市高架桥，其中绝大部分结构形式为简支梁桥结构。因此，尽早的发现简支梁桥的结构损伤并采取加固措施对于预防桥梁结构破坏，减少人民生命财产损失具有重要意义。

传统的损伤识别方法需要通过传感器测得较多的数据进行分析，传感器不仅成本高，而且精度受路面噪声和车辆行驶振动的影响，因此在实际工程中难以实现。针对这一问题，业内有专家提出了基于挠度差值影响线的损伤识别方法，该方法通过简支梁的挠度变形来判断桥梁的整体工作状态，以挠度作为参数，通过挠度差值影响线图形来判断损伤位置。本文通过软件模拟的手段对这一方法进行了试验验证，并从中发现该方法的不足。

2 基于挠度影响线的损伤识别方法

2.1 挠度影响线的计算基础

2.1.1 集中荷载下简支梁弯矩表达式

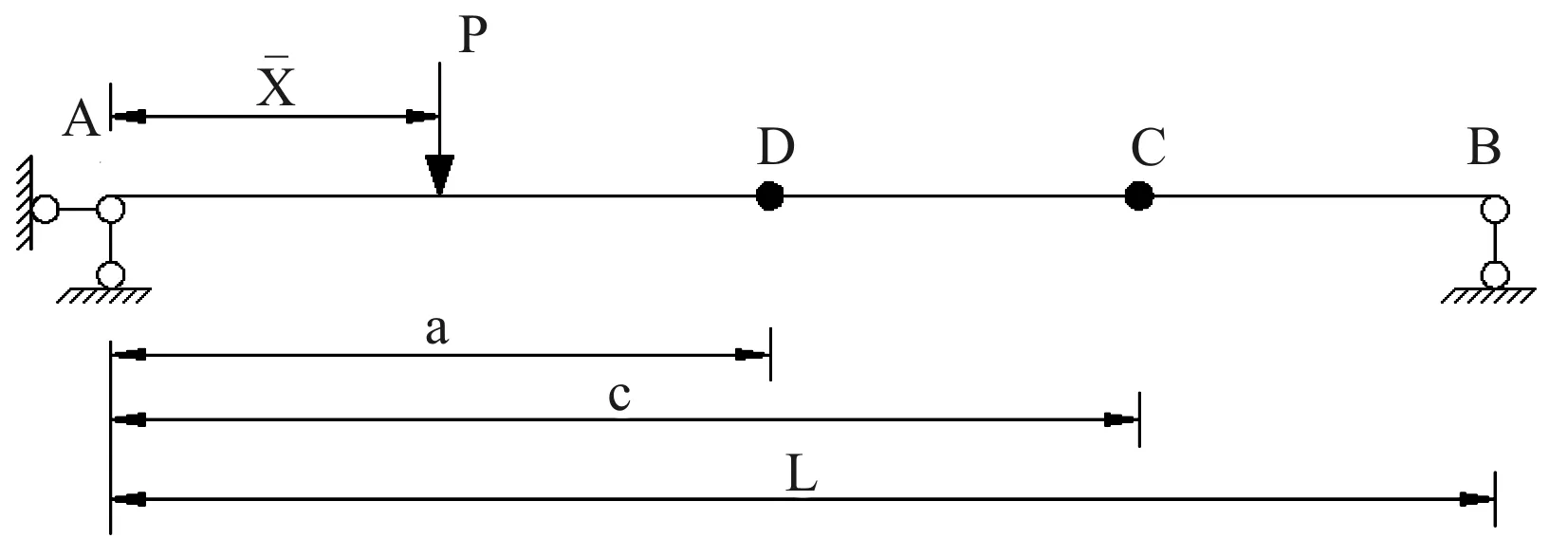
图1 移动荷载位置

图1为移动荷载位置图，由静力平衡条件可以求出荷载作用下简支梁任意截面弯矩表达式为：

(1)

已知简支梁的跨度为L，是简支梁端点A与移动荷载之间的长度，表示梁上截面据端点A的距离。

2.1.2 虚设单位荷载下简支梁弯矩表达式

图2为虚设单位荷载位置图，在该荷载作用下简支梁上任意截面弯矩表达式为：

(2)

图2 虚设单位荷载位置

2.2 简支梁挠度影响线计算公式

C点处发生局部损伤会使[c-ε,c+ε]区域梁的抗弯刚度减小。假设结构某处发生损伤前的刚度系数为EI，发生损伤后结构刚度系数变为EI′。将式1和式2带入位移计算简化公式中，即可求出测试点在移动荷载作用下的挠度影响线。

由公式(2)可知简支梁结构在虚设单位荷载作用下的弯矩表达式和所求位移点的位置有关。因此挠度影响线是与简支梁损伤位置和挠度测点位置相关的分段函数。在进行挠度影响线计算时，根据简支梁损伤位置和挠度测点位置，将结构分为四个区间，每个区间分为5个积分段进行积分求解得到简支梁挠度影响线计算公式。

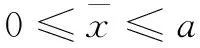
(3a)

(3b)

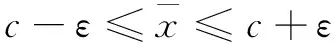
(3c)

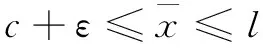
(3d)

当简支梁局部发生损伤时，损伤区域结构截面抗弯刚度减小，未损伤区域截面抗弯刚度不变。将公式3中损伤区域的积分分项中截面抗弯刚度变为，即可得到发生局部损伤后的简支梁挠度影响线计算公式。

2.3 简支梁挠度差值影响线计算公式

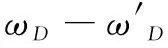
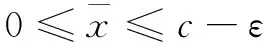
(4a)

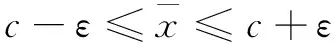
(4b)

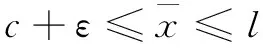
(4c)

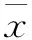
3 数值模拟计算模型

本试验所用模拟软件采用MIDAS civil。计算模型为一T型截面素混凝土简支梁共划分40个单元，41个节点，截面惯性矩为3.32×10-2m4，跨度L=20 m，采用C30混凝土。有限元模型如图3所示。

由于移动荷载作用在节点时是瞬时作用后随即消失的一种冲击荷载，在有限元软件中将集中力近似模拟为最大值为1 kN的三角形荷载如图4。根据实际计算荷载大小在定义节点荷载时输入其中的放大系数。本文计算荷载取100 kN，放大系数为100。时间t1和t2之差由荷载移动速度和所建模型节点间距确定。

对于简支梁上出现的单一位置损伤，挠度差值影响线在损伤处会出现峰值且峰值与损伤处的位置大致对应。存在两处或多处位置损伤，挠度差值影响线出现两处或多处峰值与损伤位置对应。为研究单一和多处损伤条件下，简支梁挠度差值影响线的变化规律，本文设计了四组计算模型，其中M1、M2模型为单一位置损伤，损伤区域分别为3/4位置处和端部，损伤程度均为20%。M3、M4为两处位置损伤，M3模型3/4位置处损伤40%端部损伤60%，M4模型1/2位置处损伤20%端部损伤60%。模型具体情况见表1。

图3 数值模拟计算模型

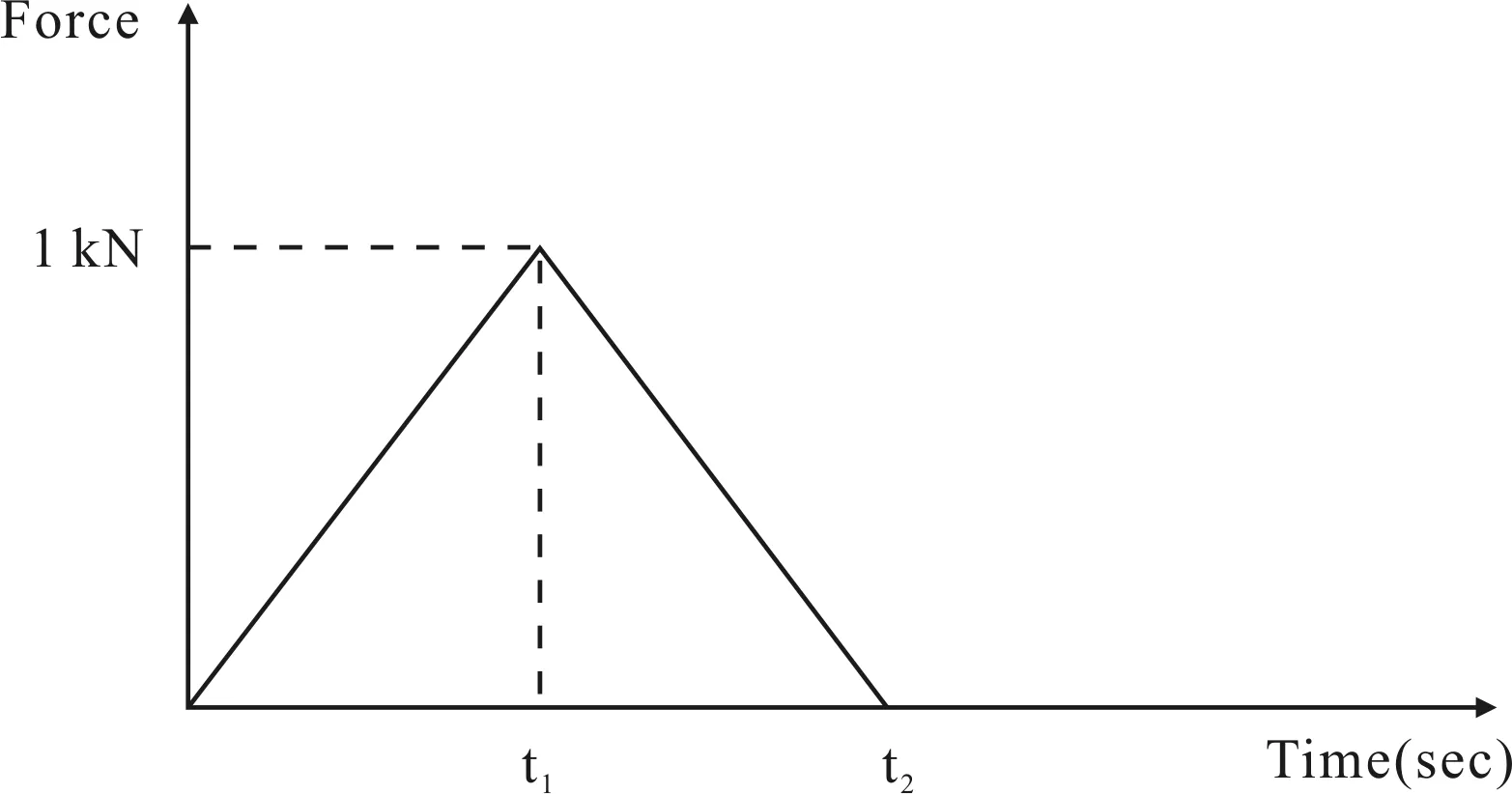
图4 移动荷载简化

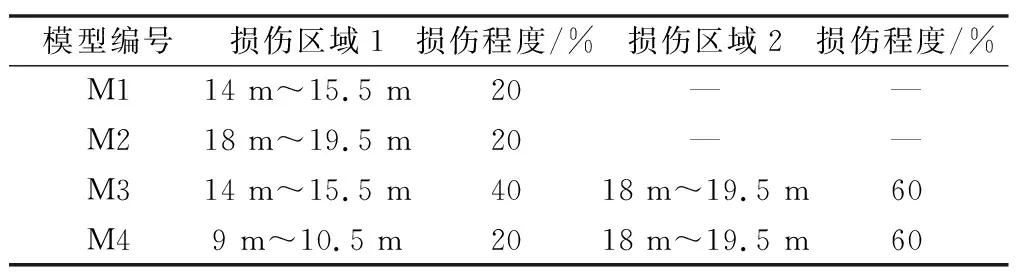
模型编号损伤区域1损伤程度/%损伤区域2损伤程度/%M114 m^15.5 m20——M218 m^19.5 m20——M314 m^15.5 m4018 m^19.5 m60M49 m^10.5 m2018 m^19.5 m60

4 数值模拟结果及分析

利用MIDAS civil软件计算出简支梁结构发生单一损伤和多处损伤时损伤前后挠度差值影响线如图5～8所示。

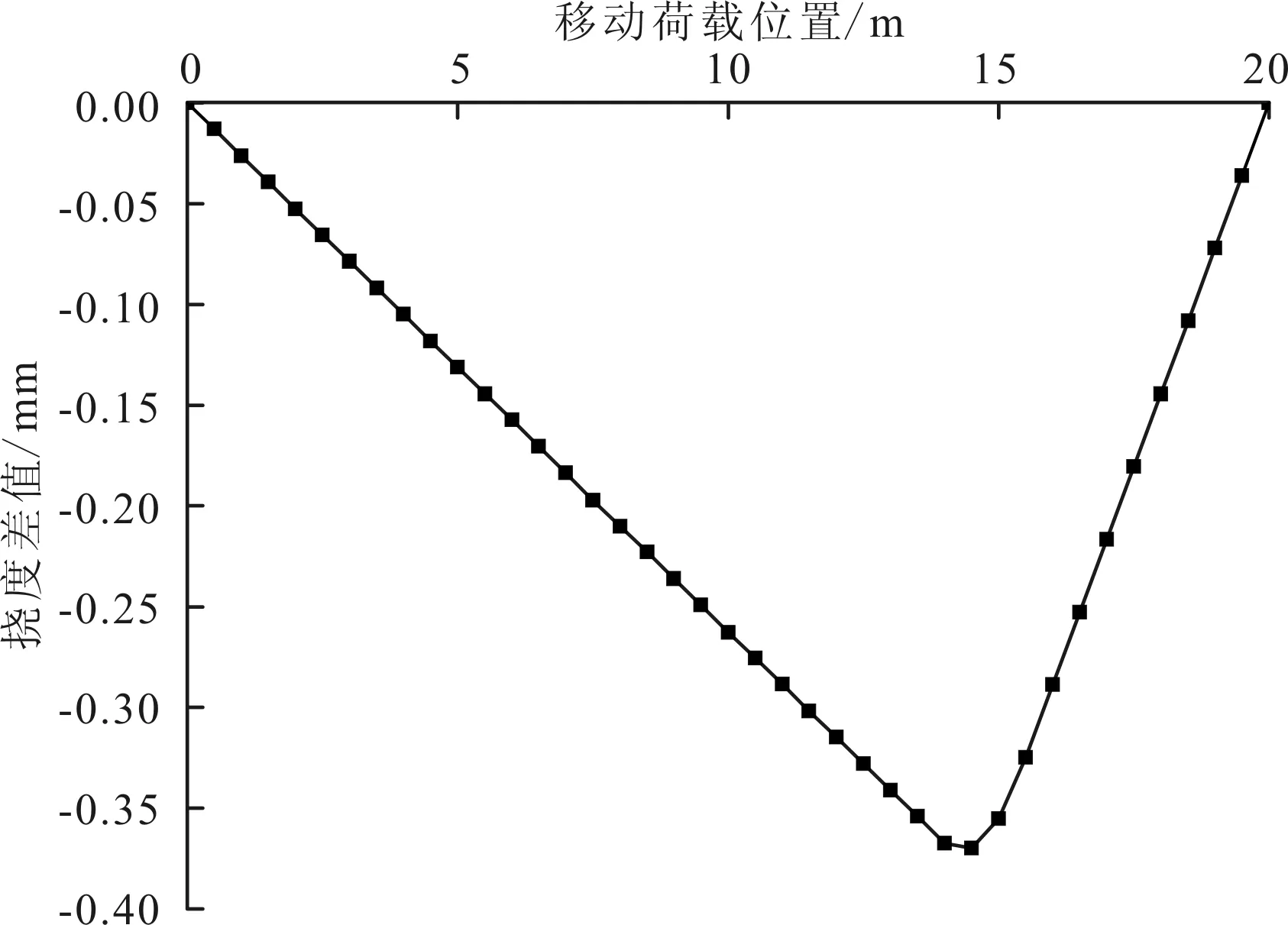
图5 M1挠度差值影响线

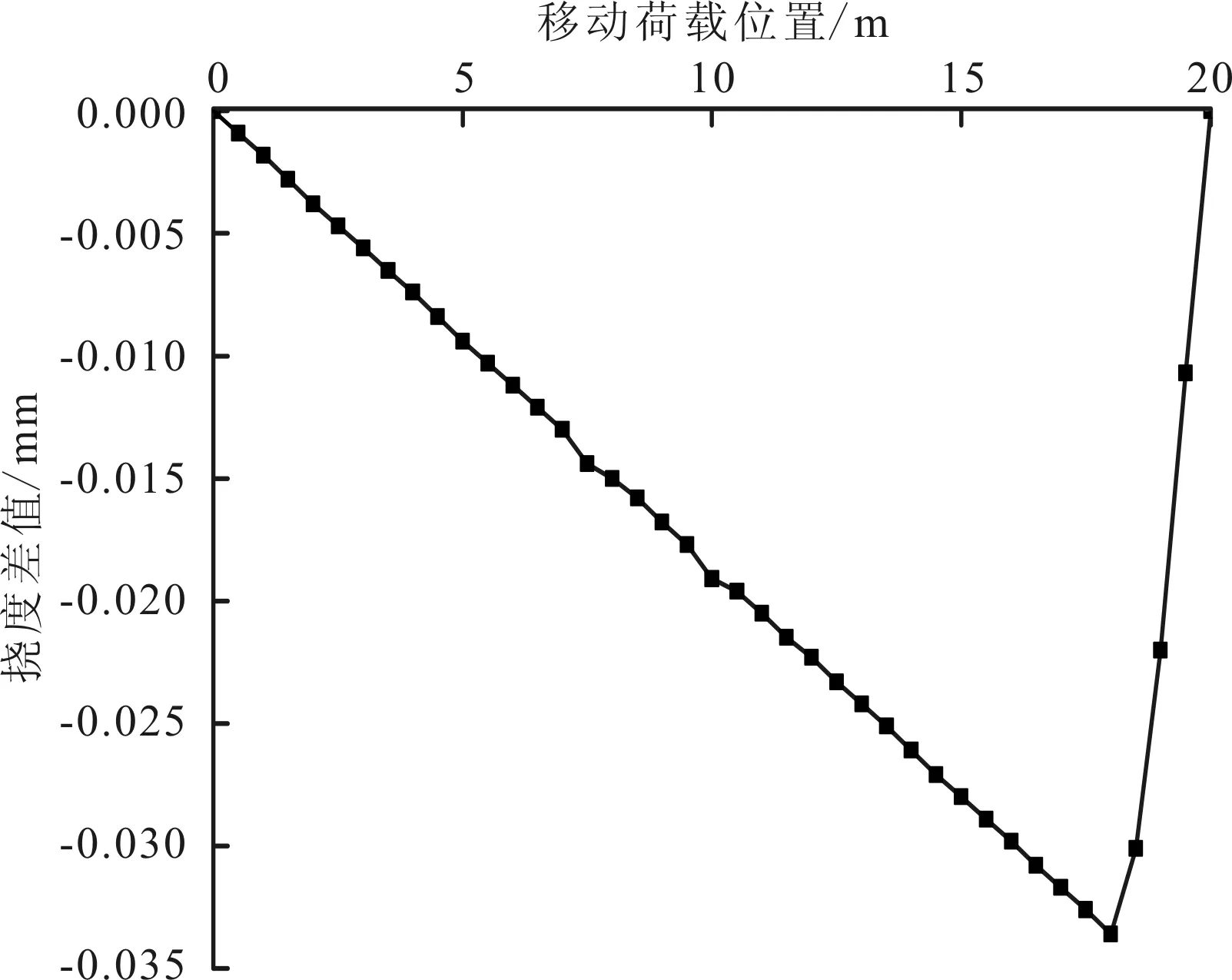
图6 M2挠度差值影响线

观察发现，对于单一结构损伤，损伤区域为3/4位置，损伤程度为20%时，挠度差值影响线的峰值出现在14 m处，大小为0.37 mm。损伤区域为端部，损伤程度为20%时，挠度差值影响线峰值出现在18 m处，大小为0.033 mm。基本符合影响线峰值与实际损伤相对应的推断。

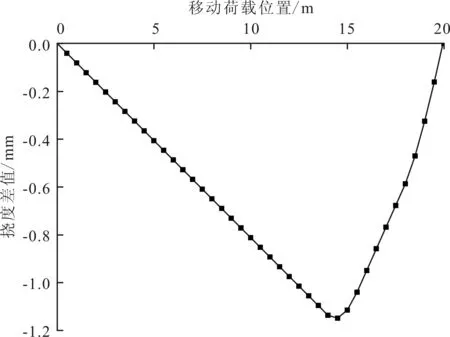
图7 M3挠度差值影响线

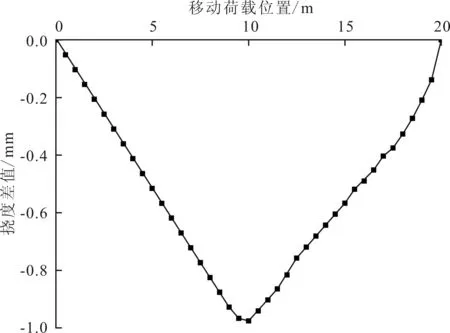
图8 M4挠度差值影响线

M3模型3/4处损伤程度为40%，端部损伤程度为60%，存在两处损伤，3/4位置处峰值为1.17 mm，端部位置损伤的挠度差值为0.3 mm。由于两处损伤位置的挠度差值影响线峰值相差过大，从图像上只能辨识出一个拐点，对端部位置的损伤无法识别。

M4模型1/2位置处损伤程度为20%，端部位置损伤程度为60%，1/2位置处峰值为0.98 mm，端部位置损伤的挠度差值为0.2 mm。由于两处损伤位置的挠度差值相差过大，导致端部位置损伤引起的挠度差值被忽略，从图中只能辨识出一个拐点。

通过对四组结果进行对比可以看出：

(1) 当简支梁存在单一结构损伤时，结构挠度差值影响线峰值的位置即为损伤发生的位置，通过挠度差值影响线图形即可判断出结构损伤的位置。

(2) 对于多处结构损伤，由于端部位置处发生损伤的挠度差值较小，会被靠近中部处损伤的挠度差值影响线峰值所掩盖，因此无法对端部的损伤进行准确的识别

(3) 相较于损伤的程度，损伤发生的位置对挠度差值的影响更大，越靠近结构中部位置，损伤所引起的挠度差值越明显。

5 结论

通过对四组模型的试验结果进行分析，得出结论：数值模拟结果表明，通过挠度差值影响线对简支梁损伤的位置进行识别的方法具有较大的局限性。当结构只存在单一损伤时，该方法效果较好，可以有效地判断出损伤发生的位置。而对于多处结构损伤，由于跨中位置损伤引起的挠度差值较端部损伤引起的挠度差值更大，端部位置损伤引起的挠度差值往往会被掩盖。只能在图像中辨识出一个拐点，无法对端部损伤位置进行辨识。在实际工程中，简支梁桥多为多处损伤，利用该方法进行简支梁损伤识别会造成对损伤位置的识别不完全。