水工隧洞爆破施工对边坡影响的数值分析

赵禄山

(国家林业局昆明勘察设计院，昆明 650216)

0 引 言

水工隧洞爆破开挖过程中，振动波不仅会造成洞身岩体变形及局部碎裂，还会继续传播影响邻近建筑物稳定性。针对隧洞爆破开挖产生振动效应的探索，国内外早已开展相关研究。引汉济渭工程是国家172项重点水利建设项目之一，汉江水需要穿越秦岭到达秦岭北麓，穿越秦岭段的隧洞埋深都在500 m以上，大埋深和超长距离成为水工隧洞技术难点，白少博、刘贵雄等以引汉济渭秦岭隧洞4号支洞为例，优化爆破开挖方式、钻爆参数，对爆破开挖技术进行了分析[1-2]；贾澄澄等基于采用动力有限元法对引水隧洞施工爆破振动效应进行数值模拟，分析探讨了爆破振动对上覆边坡的稳定性影响[3];王举以跳花坡隧道爆破为例，采用Midas/GTS有限元分析隧道洞中爆破振动对地表影响[4]。然而这些研究大多针对爆破振动对边坡整体稳定性的影响，并未对边坡不同部位受振影响进行深入研究。

本文以在建水利工程为例，采用数值模拟方法，对水工隧洞爆破开挖过程中的爆破振动对边坡不同部位的应力应变影响展开分析。

1 下埋水工隧洞的边坡模型及荷载施加

1.1 模型建立及边界设置

重庆市某水利工程为大(Ⅱ)型水利工程，任务为以灌溉、供水为主，兼顾发电等综合利用。该水利工程主要包括水库枢纽及灌溉渠系建筑物。灌区设计灌溉面积2.039 3×104hm2，工程灌溉渠系线路较长，以其中一段渠系建筑物为例进行分析，该分干渠由1座水工隧洞形成，全长2.98 km，设计流量0.89 m3/s。隧洞通过区无大的断裂切割，岩性为灰岩、白云岩等。建立该水工隧洞简化模型，见图1，圆形隧洞半径为2.6 m，坡比1∶0.5，根据地质情况，水工隧洞围岩类别分布有Ⅲ、Ⅳ、Ⅴ级。本文以奥陶系桐梓组Ⅲ级围岩为例，并假定边坡岩土体材料各向同性，不考虑地下水位的影响，围岩参数见表1。

根据结构的动力特性，利用动力平衡方程，采用直接积分法，进行动力时程分析。动力平衡方程如下：

(1)

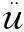
时程分析时间增量取1 ms，也即时间分析步长△t=0.001 s；总积分时间为400 ms，总时步取为N=400。

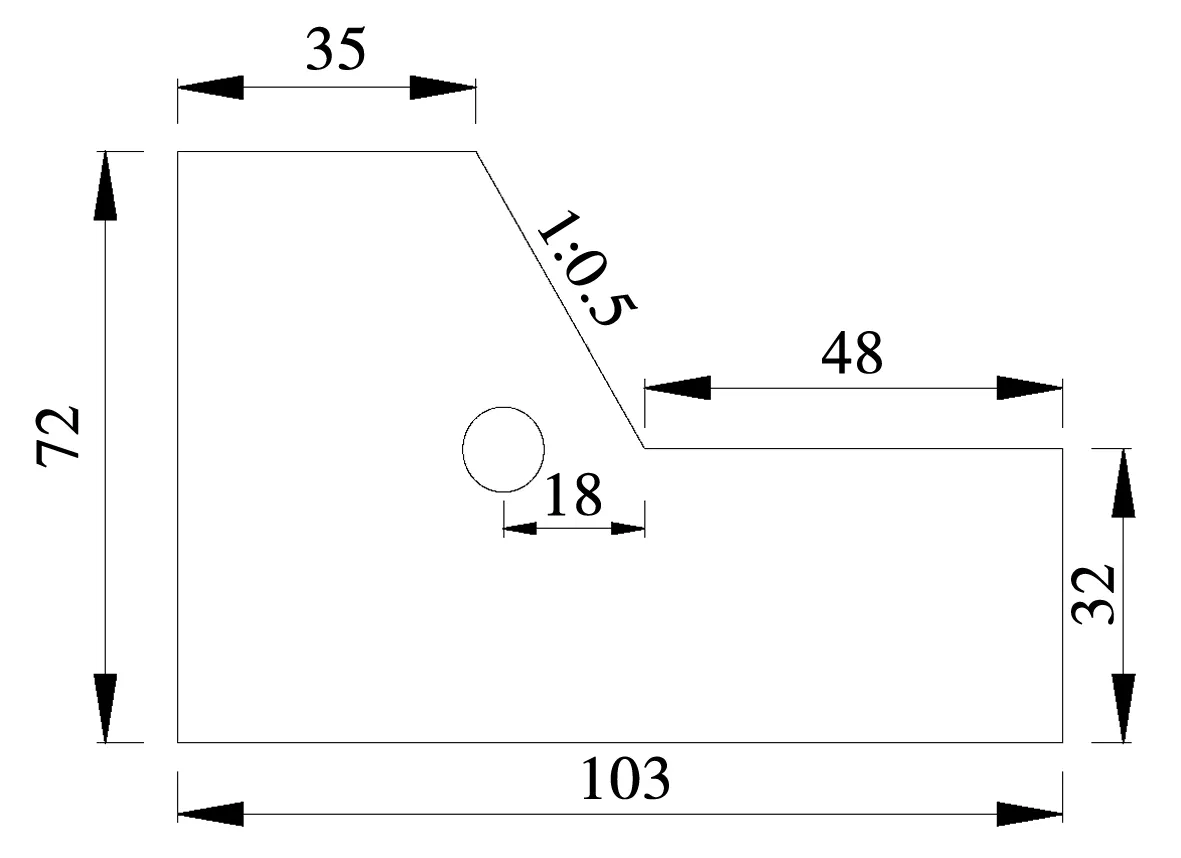
图1 模型简图(单位：m)

表1 岩体参数

1.2 爆破荷载施加

采用二维模型分析隧洞爆破过程，需将动力加载过程作用于隧洞周壁面，其运算方法是将荷载施加于隧洞周壁的单元线，图2为荷载的加载示意图。

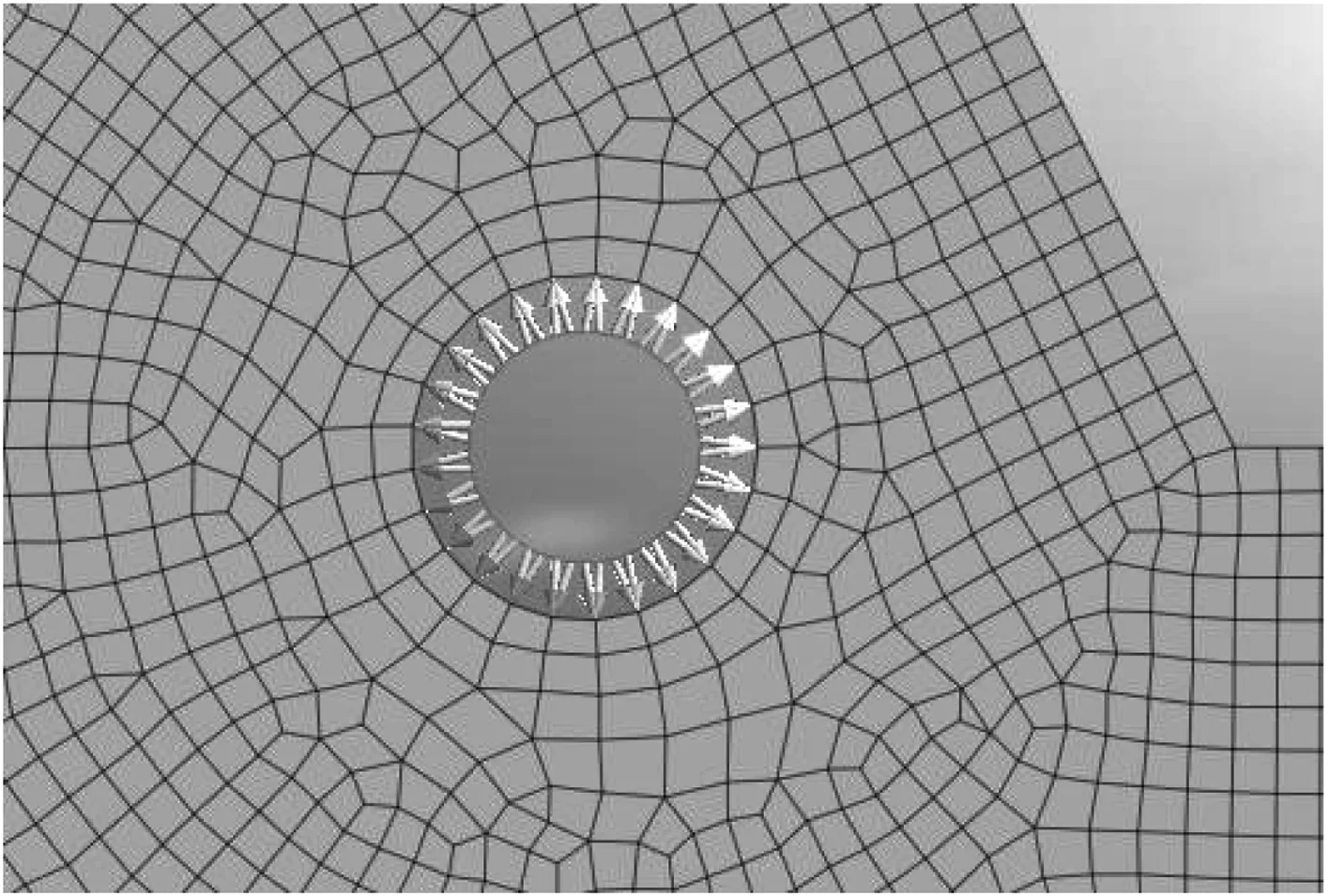
图2 荷载的加载

爆破施工采用硝铵炸药，炸药密度ρ0=1 g/cm3，爆速Vr=3 600 m/s，施工中炸药直径0.032 m，小于炮孔直径0.04 m，采用不耦合装药结构，爆破进尺2 m，单段最大药量6.4 kg。

国内外学者对炸药爆炸过程中产生的最大爆轰压力提出了多种计算方法[5]，影响最大爆轰压力的因素包括：使用的炸药类型、耦合装药或不耦合装药结构等。齐景岳[6]给出了爆炸最大爆轰压力计算式：

(2)

式中：ρ0为炸药密度；Vr为爆速。

爆破后作用于岩体界面上的最大压力并不等于最大爆轰压力，根据弹性波理论及文献[7]可求解得到不耦合装药炮孔条件下，孔壁界面的最大压力Pm计算式为：

(3)

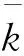
实际施工较难做到理想状态下的药卷与孔壁紧密接触，同时本工程采用不耦合装药，因此基于单孔装药量与炮孔体积直接的关系，计算得到不耦合装药下的孔壁压力峰值为：

式中：n为单孔药卷数；A0为药卷横截面积；l为药卷长度；A1为炮孔横截面积；L为炮孔长度。

爆破荷载曲线采用简化的荷载-时间历程三角形曲线，达到爆破峰值压力时间为4 ms，爆破过程总时长为67 ms。

2 计算结果

2.1 应力波变化

通过数值模拟，得到爆破过程中不同时刻的应力云图，见图3，从应力云图可分析隧洞爆破时边坡中的总应力波的传播变化情况。

从应力云图可以发现，动力加载过程是荷载沿圆周作用于隧洞周壁面并向外扩散，在2 ms到4 ms这段时间，应力波由隧洞逐渐向四周扩散，压应力波的范围逐渐扩大。从6 ms时边坡应力波分布情况可见，该时刻压应力波已扩散至坡面。从6和8 ms时的应力分布情况可发现，由于压应力传播至边坡临空面后发生反射作用，很快便形成反射的拉应力波。但在整个过程中，拉应力区的范围呈现出先增大后减小的趋势。坡脚处压应力在爆破过程中一直持续偏大。边坡模型中各单元应力值呈现先增后减的特征。

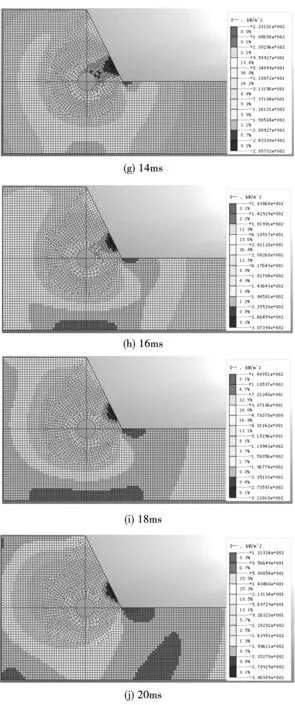
图3 应力波传播过程

2.2 位移变化

位移时程变化云图见图4。如前文应力波传播规律，爆破后振动波同时向四周传播，在6 ms时，振动波传递至边坡坡面；在8 ms时，振动波传递至边坡的坡脚地面处，从位移时程云图可见边坡坡面的位移较坡脚更大。随着时间的增加，振动波迅速传播至边坡坡顶及整个模型周边。

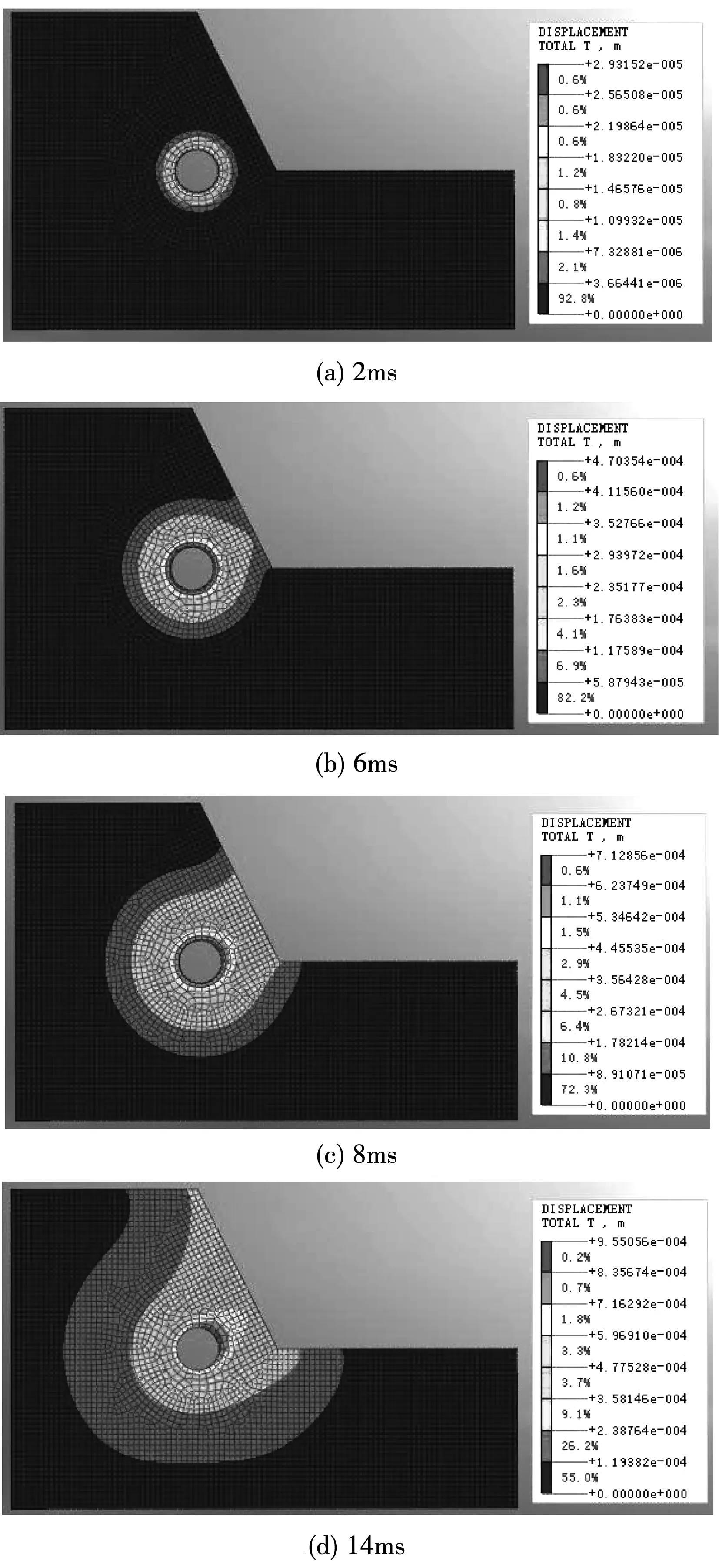
图4 位移时程云图

2.3 坡脚处平面振速时程变化

应力波作用导致岩体质点振动，判断质点振动强度的一个重要指标是振速，因此对质点的垂直振速进行监测分析，进一步探明水工隧洞爆破作用对边坡的影响情况。

在隧洞坡脚地面依次设置1～5测点(图5)，并依次给出每个监测点的垂直振速时程曲线，见图6。从时程曲线图6可以发现，1#点的振幅最大，但是频率最小；监测点的振速峰值随着距边坡坡脚距离增大而减小，振动频率则随着距边坡坡脚距离增大而同步变大。

图5 坡底监测点

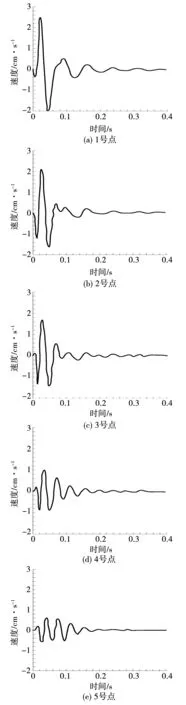
图6 监测点垂直振速时程曲线

2.4 坡顶振速时程变化

为了判断爆破振动对整体边坡的影响，同理在边坡坡顶面从左向右依次设置1～5号测点，见图7。同理依次给出每个监测点的垂直振速时程曲线，见图8。从时程曲线图8可以发现，5#点振幅最大，但是频率最小；在坡顶处振速峰值随着与坡肩距离的增加而逐渐减小，振动频率随着与坡肩距离的增加同步逐渐变大。

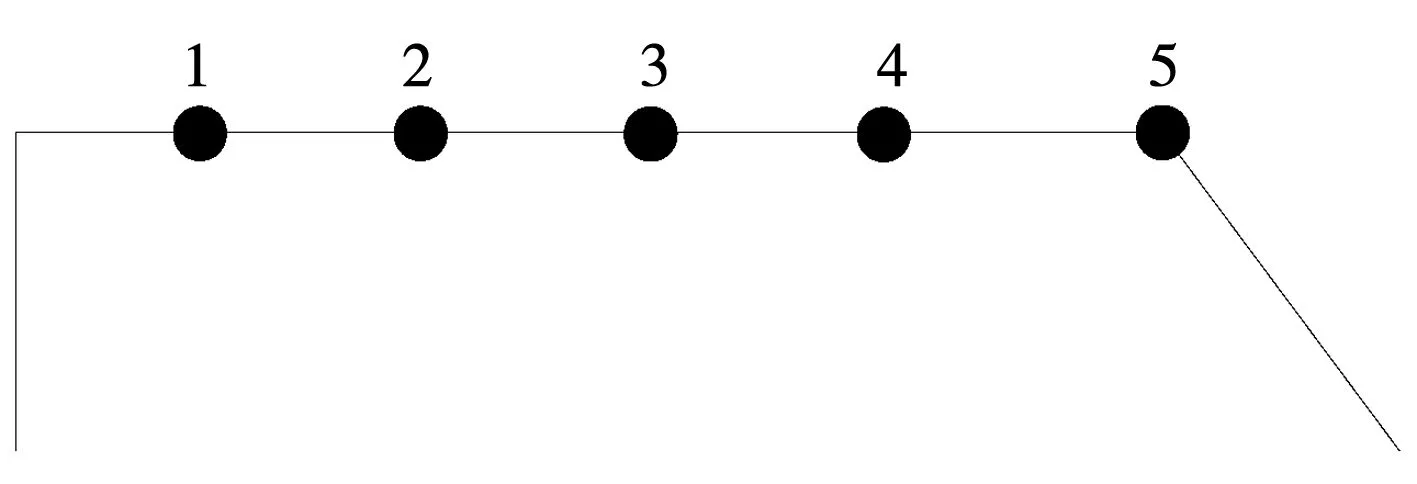
图7 坡顶面监测点

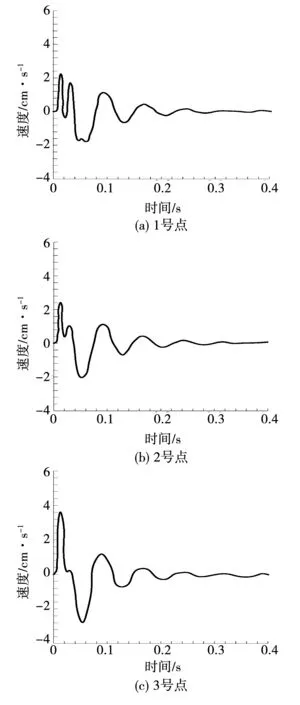
图8 坡顶面监测点垂直振速时程曲线

从边坡坡脚与坡顶测点的垂直振速时程曲线图对比分析可以发现，在水工隧洞爆破掘进时，坡顶的振速明显大于边坡坡脚。

3 结 论

1) 分析了隧洞爆破施工过程对边坡的振动影响。采用数值模拟方法，以在建工程为例，建立水工隧洞-边坡简化模型，研究爆破振动对边坡不同部位的应力应变影响。

2) 初爆瞬间动力荷载沿圆周作用于隧洞周壁面并向外扩散，压应力波的范围逐渐扩大。当压应力波扩散至坡面后将发生反射作用并形成拉应力波，拉应力区的范围呈现出先增大后减小的趋势。坡脚处压应力在爆破过程中一直持续偏大。在爆破过程中，边坡中各部位应力值呈现先增后减的特征。边坡坡面的位移较坡脚更大。

3) 监测点的振速时程曲线规律表明,在边坡坡脚及坡顶，振速峰值随着距坡脚及坡肩距离增大而减小，振动频率则反之，同时坡顶振速明显大于坡脚。