循环荷载下胶凝砂砾石材料的滞后及阻尼效应

2018-11-02张献才韩立炜

建筑材料学报 2018年5期

黄虎, 黄凯，张献才，韩立炜

(1.华北水利水电大学水利学院，河南郑州 450045； 2.河南省水工结构安全工程技术研究中心，河南郑州 450045； 3.河南省豫东水利工程管理局三义寨分局，河南开封 475000)

胶凝砂砾石(cemented sand and gravel, CSG)材料是一种将水、胶凝材料、河床砂砾石或开挖废弃料等当地材料混合，然后利用简易设备和工艺进行拌和后得到的新型筑坝材料.近年来，CSG坝在希腊、日本、土耳其[1-3]都有所应用.2004年，中国在贵州省松道塘水库上游过水围堰工程中首次采用 CSG坝方案，此后在福建白沙、街面和洪口3个水电工程中的上、下游围堰相继采用.随着近年来大量理论成果的进展，2014年，中国第一座永久性CSG建筑物——守口堡大坝在山西省开工建设.目前，国内外在CSG材料的静力学特性和本构模型研究方面取得了大量有价值的成果，但关于其动力学性能方面的研究主要集中于材料的动模量和阻尼比.Omae等[4]采用动三轴仪测试了Takizawa坝的筑坝材料动力性质，认为在小幅值循环压力作用下，CSG材料的动剪切模量随围压增大而增大，材料动力本构关系表现出明显的非线性性质，随着剪应变增大，材料动剪切模量减小.Haeri等[5]通过不排水动三轴试验研究，认为水泥含量对CSG材料的最大剪切模量和阻尼比影响不大；随着偏应力的增大，材料的阻尼比增大而剪切模量降低；围压越大，材料的剪切模量越大而阻尼比越小.明宇等[6]采用大型动三轴试验研究了不同胶凝材料掺量下CSG材料的动力特性，给出了胶凝材料掺量、围压对CSG材料动力特性影响的变化规律，推导了非线性动弹性模量及阻尼比的表达式.傅华等[7]通过对不同胶凝材料掺量的CSG材料进行动三轴试验，发现其动力学指标随着胶凝材料掺量和养护龄期的增加得到了一定提高；随着围压、固结应力以及动应力的提高，其动永久变形量相应增大.蔡新等[8]基于动三轴试验，研究了不同围压、不同胶凝材料掺量下CSG材料的动本构关系及动模量衰减规律.

以上文献对CSG材料阻尼比变化规律的研究主要集中在小应变状态下，而对循环加载过程中应力-应变的滞后关系、滞回环演化规律鲜有提及.根据相似材料的研究经验[9-10]，循环荷载下材料的变形和破坏是一个损伤不断产生、累积的过程，也是能量不断耗散的过程，而耗散能的变化可以从滞回环的演化入手；滞回环的形态不仅反映了循环加卸载过程中力和变形、阻尼等特性，同时材料的动弹性模量、阻尼比、能量耗散等动力学参数也是通过滞回环求得的.Tutuncu 等[11-12]利用单轴应力循环试验分析了影响沉积岩非线性弹性行为的一些主要因素，认为滞后机制是由于裂纹表面和颗粒边界之间的摩擦滑动引起的.肖建清等[13]通过花岗岩常幅循环加载试验，探讨了滞回环可能存在的形态，认为滞回环形态有椭圆形、新月形和长茄形，主要取决于应变相位和应力相位的关系.何明明等[14]通过常幅循环荷载试验揭示了阻尼比随循环次数的演化规律，认为应力上限会影响阻尼比的发展规律，在加卸载过程中阻尼比随着循环次数的变化而变化.从CSG材料自身的特性来看，受到砂砾石形状和低掺量胶凝材料的影响，其自身孔隙率远大于常规土体和岩石，动力学特性也与一般材料存在差别.要想充分认识CSG材料的动力学性能，探明其在动荷载下的滞回环及相应动力学参数的演化规律，需要从CSG材料在循环荷载下的滞后特性和滞回环入手，研究整个循环过程中材料参数的变化规律.本文利用大型动三轴试验系统，对循环荷载下CSG材料的滞后特性进行了研究和分析，根据滞回环的特征和演化规律，基于能量原理对新月形滞回环的阻尼比进行了讨论，得出了整个循环过程中CSG材料的阻尼比演化规律，为进一步认识CSG材料的动力学特性奠定基础.

1 试验

1.1 试验材料

CSG试件由水泥、粉煤灰、砂砾石和水按一定比例混合制备而成.水泥采用普通硅酸盐水泥；根据GB/T 50146—2014《粉煤灰混凝土应用技术规范》对粉煤灰品质的要求，粉煤灰采用中国郑州热电厂干排F类 Ⅱ 级粉煤灰，比表面积为506m2/kg；砂砾料取自汝州市汝河河床，为减小因材料不均匀而造成试件力学特性波动太大的影响，将砂砾石混合料筛分，以便优选砂率进行配合比试验，骨料采用二级配；水为自来水.根据SL 678—2014《胶结颗粒料筑坝技术导则》，胶凝材料用量不宜低于80kg/m3，其中水泥熟料用量不宜低于32kg/m3，水胶比(mW/mB)宜控制在0.7～1.3，胶凝砂砾石中砂率(质量比)宜为0.18～0.35.试验采用的CSG材料配合比设计参数见表1.

1.2 试件制备及试验设备

CSG试件为φ150×300mm的圆柱体，将砂砾石、水泥、粉煤灰和水按表1所示配合比放入搅拌机搅拌均匀，装入钢模具内，采用人工结合机器的振捣方式，48h后成型脱模，置于标准养护室内养护至规定龄期(28d).

试验设备采用美国GCTS公司生产的 STX-600 型动三轴仪，该仪器由液压站、数字信号调节控制单元、荷载架和三轴压力室、压力/体积控制器以及CATS软件5部分组成.荷载架最大可以提供300 kN 的轴向力，三轴压力室可以承受最大 2 MPa 的压力.

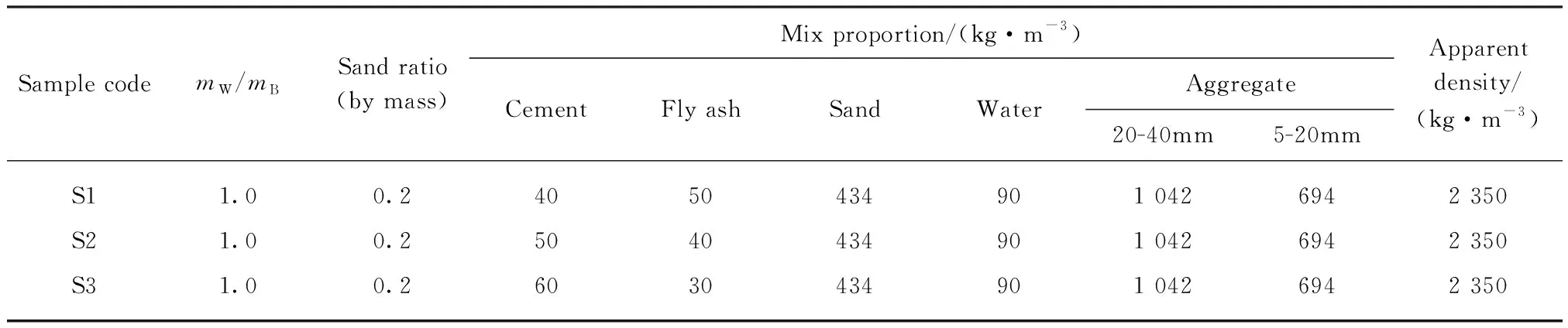
表1 CSG试件配合比设计参数

1.3 试验加载方式

考虑水利工程遇到的动荷载类型主要为地震和波浪荷载，加载波形设为正弦波，频率为1.0 Hz.根据静力学试验结果[15]，材料的弹性极限强度为其峰值强度σd的75%，因此，为了得到足够的循环次数，等幅循环试验的上限循环应力σup控制在75%σd以下；选定3组应力水平，以等幅值的正弦波方式施加循环荷载，直至试件破坏，记录荷载的循环次数；当试件应变达到10%时停止.

2 非线性滞后特征分析

2.1 累积应变与循环次数关系

CSG材料的峰值强度与水泥含量有密切关系，水泥含量越大，材料峰值强度越大[16].故根据水泥含量不同，试验时上限循环应力σup取试件σd的 50%～ 70%.图1是各试件在循环荷载下的累积应变和循环次数关系曲线.由图1可知，各试件的应变均表现出三阶段特征：初始阶段、等速阶段和加速阶段.每个阶段在整个循环中的长度不同，初始阶段最小，出现在前3个循环，此时变形速率迅速衰减；等速阶段循环次数最多，变形速率基本为恒定值，该阶段的长短与加载的上限循环应力大小密切相关，上限循环应力越小，等速阶段越长；当应变接近临界破坏应变时，变形速率迅速增大，循环进入加速阶段，经历两三个循环后，试件破坏.

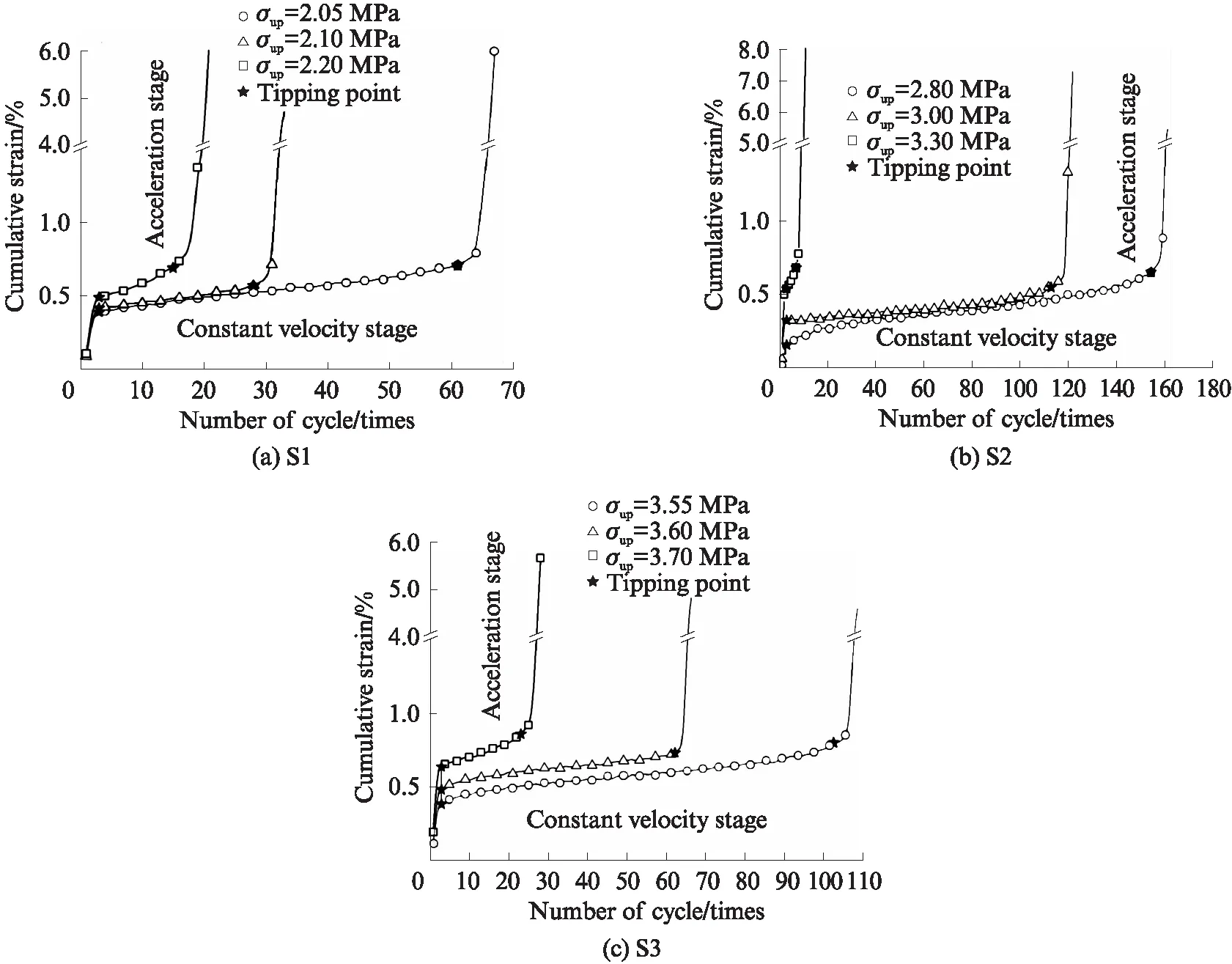
图1 各试件在循环荷载下的累积应变与循环次数关系Fig.1 Accumulated strain-cyclic number curves of samples

从整个应变的变化过程看，不同阶段间存在明显的临界应变值，且临界应变值与水泥含量及上限循环应力的大小密切相关.从每个阶段经历的循环次数看，初始阶段的循环次数相同；在等速阶段，上限循环应力越接近75%σd，循环次数越少，加速阶段循环次数也越少，试件达到临界破坏应变后破坏越迅速.水泥含量越高，试件的临界破坏应变越大.

2.2 非线性滞后分析

基于上述累积应变分布的三阶段划分，以试件S1为例，对不同上限循环应力下不同应变阶段的应力-时间和应变-时间曲线进行归一化处理，如图2所示(其中L01，L02等分别表示第1个，第2个等滞回环).由图2可见：在整个循环过程中，应力与应变曲线并不重合，在循环的加载阶段，应变曲线一部分超前于应力曲线，应力与应变的相位差为负值，而应变曲线的另一部分滞后于应力曲线，两者相位差为正值，且与循环次数有关；在循环的卸载阶段，应变曲线滞后于应力曲线，应力与应变之间的相位差为正值.应变曲线在第1个和最后1个循环出现了明显改变，呈非正弦分布.

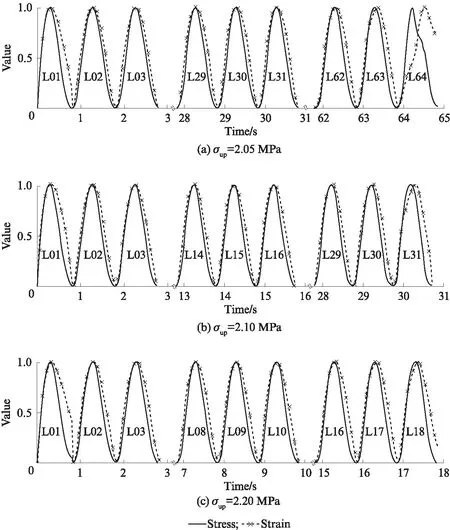
图2 试件S1的应力-时间和应变-时间曲线Fig.2 Stress-time and strain-time curves of sample S1

在不同阶段，单个滞回环的应力峰值和应变峰值的相位差表现出不同的特征，可能为零，也可能为正值.如果应力与应变的相位差为零，说明应力与应变的相位相同，表明材料是线弹性的，且不存在滞后现象；如果应力与应变的相位差不为零，则表明在循环荷载作用下材料产生了滞后效应，相位差的大小表现了材料偏离线弹性性质的程度和产生滞后效应的强弱[17].图2中，试件S1在初始阶段的应变峰值滞后于应力峰值，应力与应变的相位差为正值且逐渐减小；在等速阶段前期，二者相位差仍为正值，并逐渐减小；当接近总循环次数的一半左右时，应变峰值与应力峰值几乎重合，二者相位差为零，随后，应变峰值滞后于应力峰值的程度又逐渐增大；当进入加速阶段后，应变峰值滞后于应力峰值的现象越来越明显，应力峰值和应变峰值的相位差迅速增大，在试件破坏前的1个循环，应变曲线与应力曲线不再保持一致，滞后现象突出.从试件S1的整个循环过程来看，随着循环次数的增大，加载阶段应变与应力相位差为负值的部分由大—小—大，当应力峰值与应变峰值的相位差为零时，对应循环加载段的应变与应力相位差全部为负值，这与单个循环滞回环产生的塑性变形密切相关，单个循环的塑性变形越大，应变滞后于应力的程度越大.根据分析结果，试件S2，S3的应力、应变与时间关系也存在相同的特征，限于篇幅限制，这里不再给出具体的结果.

由于CSG材料中骨料形状的不规则，加上低含量的胶凝材料不能完全充填骨料间的缝隙，使得材料内部分布着许多裂纹、孔洞以及微结构边界，从而导致了其非线性弹性行为和显著的滞后特征.当上限循环应力与峰值强度的比值较小时，在一定时期内，试件处于压实过程，试件内部空隙和微裂纹逐渐闭合，并产生塑性变形，且该变形随着循环次数的增加而逐渐减小；当压实到一定程度后，试件内部新微裂纹萌生，新的塑性变形出现，且随着新微裂纹的发展和贯通而逐渐增大，当接近试件的疲劳寿命时，塑性应变达到最大.当上限循环应力与峰值强度的比值较大时，由于上限循环应力接近试件的屈服强度，试件内部原始微裂纹的闭合过程与新微裂纹的产生过程没有明显的分界点，存在重叠期，从而使整个循环过程中的塑性变形均较大，应变峰值始终明显滞后于应力峰值.前1次循环的塑性变形导致当前循环加载段的应变超前于应力，而当前循环过程中产生的塑性变形导致卸载段应变滞后于应力.

图3给出了等速阶段中各试件在不同上限循环应力下单个滞回环所对应的塑性应变.由图3可知：随着循环次数的增加，单个循环的塑性变形均先减小后增大，即滞回环下部开口先减小后又增大；当上限循环应力较小时，塑性应变的最小值接近零，滞回环几乎闭合；当上限循环应力较大时，滞回环张开明显.累积塑性应变整体呈增大的趋势，说明塑性应变的存在是导致加载段应变相位超前于应力相位的根本原因.

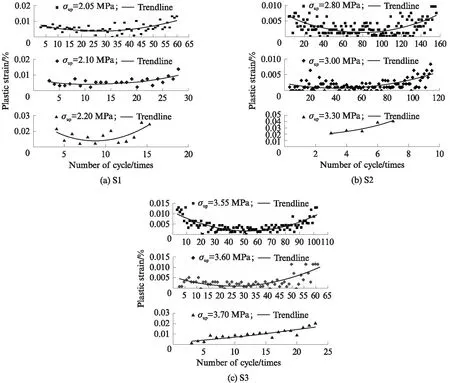
图3 单个循环塑性应变分布Fig.3 Plastic strain distribution of single loop

2.3 滞回环形态分析

由于CSG材料自身结构特点的影响，在循环加载过程中几乎每个循环都会有塑性变形产生，从而造成滞回环的不闭合.图4给出了各试件在不同应变阶段的单个滞回环形态.由图4可以看出，初始、等速和加速阶段滞回环下部的不闭合程度不同，初始阶段和加速阶段较大，说明在开始和结束前的几个循环中，塑性变形以及消耗的能量都比较大.

图4 试件S1，S2，S3的典型滞回环Fig.4 Typical hysteresis loops of sample S1, S2, S3

在1个完整循环周期内，若应变始终滞后于应力，则滞回环呈椭圆形；若加载段应变超前于应力，卸载段应变滞后于应力，则滞回环呈新月形；若加载段应变既有滞后于应力部分，也有相等和超前部分，则滞回环呈长茄形[13].根据以上分析，CSG材料的应力相位与应变相位在加载段和卸载段存在明显不同，应力与应变相位差在加载和卸载时并不相等，这说明滞回环顶部应力方向反转时刻对应的应变相位进行了调整，因此应力-应变滞回曲线在荷载反转处是尖叶状的，不是椭圆形的，滞回环为新月形，向应变增大的方向凸出.滞回环的形态不仅取决于加卸载过程中的塑性变形，还受到材料黏滞性的影响，而材料黏滞性主要受到其内部液体和颗粒摩擦的影响.本试验过程中的试件均为干燥试件，故可忽略内部水产生的黏滞作用.但从各试件滞回环的演化过程来看，除了加载的第1个循环外，随着循环次数的增加，初始阶段和等速阶段的新月形滞回环均比较扁薄，在接近破坏前的几个循环逐渐趋于宽厚，滞回环的顶部由尖叶状向椭圆形变化，说明破坏前的滞回环受到材料黏滞性的影响较大，主要原因是试件破坏前内部出现了大量裂纹，导致胶结键断裂，骨料间的摩擦使材料表现出了黏滞性.材料黏滞性对滞回环的影响在试件内部出现大量裂缝以后表现明显.

2.4 滞回环的描述

为分析每个滞回环的演化规律，根据单个滞回环加卸载段的应力-应变关系，将试验数据采用分段的方式进行描述.限于篇幅限制，以试件S1，上限循环应力σup为2.05MPa时的典型滞回环为例，将每个滞回环分为加载段和卸载段，对各段曲线进行拟合(见图5)，进而描述循环过程中加卸载段的应力-应变关系.

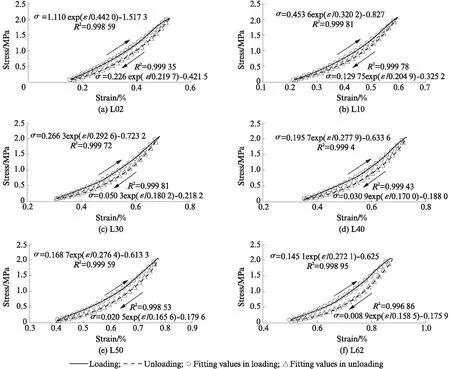
图5 试件S1的典型滞回环拟合曲线Fig.5 Fitting curves of typical hysteresis loops of sample S1 (σup=2.05MPa)

由图5可知，对于不同的单个滞回环而言，加卸载段应力-应变均可描述为以e为底的指数函数，即：

(1)

式中：σ为单个循环的应力；ε为单个循环的应变；a，t，b为拟合参数.

典型滞回环加载段和卸载段的拟合参数a，t，b与循环次数的关系如图6所示.由图6可知：随着循环次数的增加，拟合参数呈非线性减小；在循环初期拟合参数的减小速率较大，经历20个循环后，拟合参数的减小速率逐渐变小；随着循环次数的增加，同一参数在加载段的变化幅度大于卸载段；t的变化速率明显小于a和b.

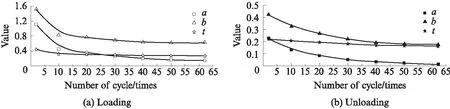
图6 加卸载段拟合参数与循环次数关系Fig.6 Fitting parameters and cycle number curves

3 阻尼比分析

阻尼比是进行材料动力反应分析时必不可少的参数之一，是衡量材料吸收振动能力的一个重要指标.DL/T 5355—2006《土工试验规程》针对对称性椭圆形滞回环的阻尼比(λ)给出了如下的计算公式：

(2)

式中：A为滞回环的面积，表示单个循环消耗的能量；As为峰值应力、对应应变和椭圆中心围成的面积，4As表示1个周期内所储备的最大弹性应变能.

目前针对岩土和混凝土材料的阻尼比大多基于式(2)进行计算，由于新月形和长茄形滞回环上下左右都不对称，因此严格意义上并不符合式(2)的前提条件.

从能量角度出发，在循环加载过程中，吸收的能量一部分形成弹性应变能，另一部分则以声能、热能、辐射能以及新塑性区产生所需要的能量等形式消耗掉，即耗散能，损耗的能量一部分用于微裂纹的萌生和扩展，一部分用于克服阻尼力做功.能量耗散是反映材料内部微缺陷不断闭合、新裂纹萌生和发展演化的本质属性.根据能量守恒原理，假设材料单元在外力作用下产生变形时与外界没有热交换，则外力功产生的总输入能量U为：

U=Ue+Ud

(3)

式中：Ue为可释放的弹性应变能；Ud为单元耗散能.

根据上述滞后性分析，在加卸载过程中，CSG材料在不同循环中存在不同的滞后效应，其在循环加卸载过程中的典型滞回环曲线见图7.其中：加载阶段的应力极值点为B点，应变极值点为C点；卸载段的应力极值点为D点，应变极值点为E点.由图7可见，应力极值和应变极值不同步，滞回环不闭合，存在滞后和残余变形，且滞后程度和残余变形随着循环次数的增加而变化.在循环加载过程中，从A点至B点的加载段，试件的应力、应变都在增大，外力对试件做正功；达到B点后，试件的应力减小，但是由于滞后效应，其应变继续增大至C点，故BC段的变形仍然是外力对试件做正功；从C点开始，试件的应变开始减小，直到D点，其应力、应变都减小，试件向外释放弹性应变能，外力对试件做负功；达到D点后，试件的应力反向增大，但是由于滞后效应，其应变继续减小，直至达到下限应变极值E点，因此，DE段的变形仍然是外力对试件做负功.

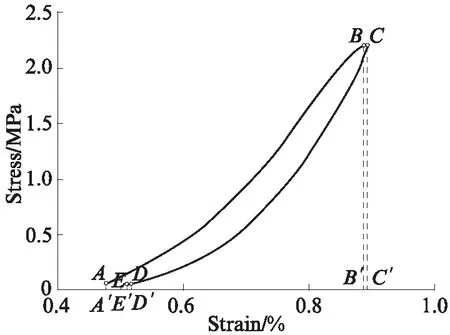
图7 循环加卸载典型滞回环曲线Fig.7 Typical hysteresis loop under cyclic loading and unloading

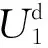
针对单个滞回环，将加卸载方程(1)代入式(3)，得到单个滞回环的耗散能，即：

(4)

根据阻尼比的定义，式(2)可修改为耗散能与弹性应变能之比再除以π，即：

(5)

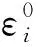
采用式(5)得到各试件的阻尼比演化曲线如图8所示.由图8可见，阻尼比曲线也可分为3个阶段，整体上呈U型：第一阶段阻尼比快速下降，阻尼比位于0.025～0.090之间，特别是第1个循环的阻尼比最大；经历3个循环后，进入第二阶段，阻尼比位于0.025～0.035之间，此时阻尼比呈先下降后上升的抛物线形分布；当进入第三阶段后，阻尼比又快速增大，阻尼比位于0.030～0.100之间，且在试件接近破坏时呈陡然上升趋势.同时上限循环应力和水泥含量对试件的阻尼比存在一定影响，水泥含量相同试件的上限循环应力越大，其阻尼比越大.

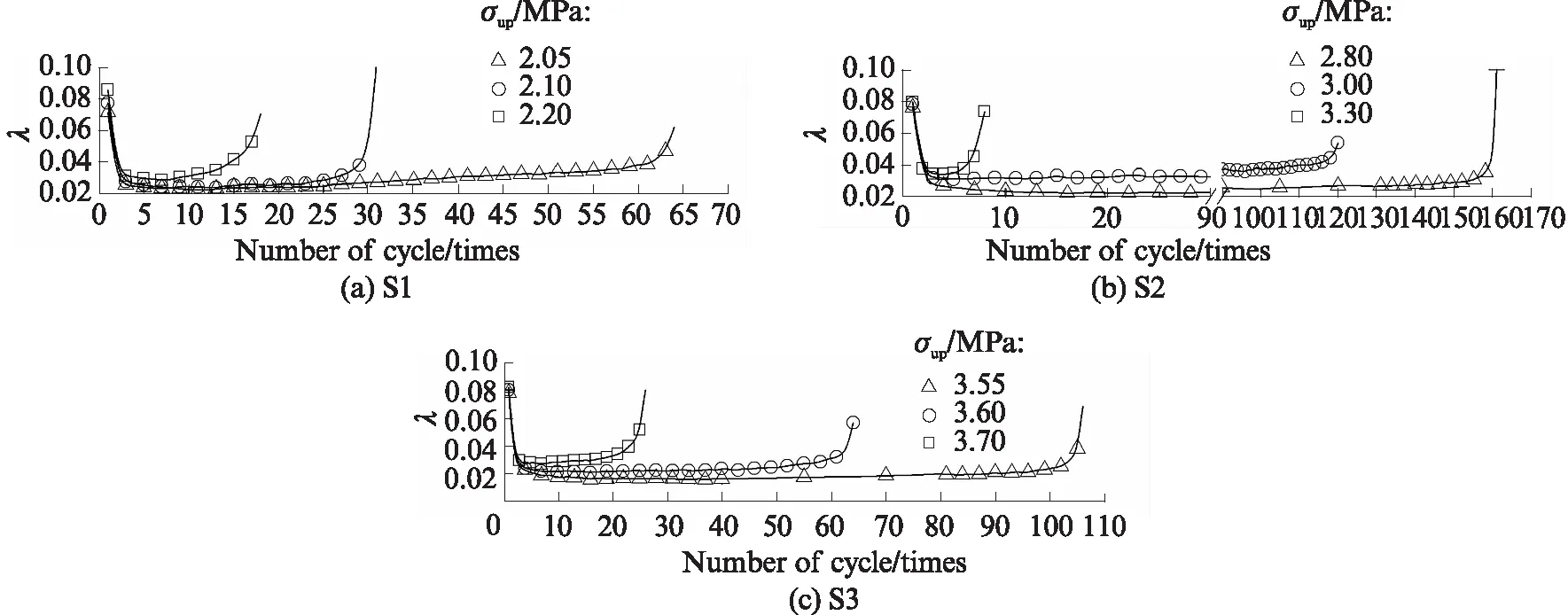
图8 各试件的阻尼比演化曲线Fig.8 Evolution curves of damping ratios for different samples

在加载初期的第一阶段，试件处于初期压密状态，直观表现为滞回环的面积和底部张开相对较大，残余变形和能量消耗较大(第1个循环尤为突出)，由此形成的阻尼比也较大.第二阶段，由于试验为等幅循环加载，同一上限循环应力下，总能量输入基本相当，每个滞回环的面积也基本相同，试件的塑性变形随着循环次数的增加而变化(见图3)，从而使阻尼比随其塑性变形(单个滞回环的残余变形)的变化而变化.第三阶段，由于试件临近破坏，内部出现了大量裂缝，滞回环塑性变形增大，微结构面间的摩擦消耗了大量的能量，特别是破坏前1个循环，以致于形成了较大的阻尼比.

综上，每个循环都存在不同程度的残余变形，能量的耗散一部分用于克服阻尼力做功，一部分用于残余变形的产生，故残余变形对阻尼比的影响不可忽视；阻尼比的大小由残余变形和滞回环面积共同决定，同时残余变形还影响了阻尼比在整个加卸载过程中的变化形态.在试验过程中第一阶段和第三阶段历时较短(一般在3个循环左右)，在工程实际应用时，由于固结沉降作用可使材料内部的部分原始缺陷处于闭合状态，因此在不考虑极限使用状态的情况下，可参考第二阶段的阻尼比取值，即认为胶凝砂砾石材料的阻尼比位于0.025～0.035之间.